瞬变电磁场模拟中的CPM L吸收边界条件

姜彦南, 刘 文, 王 娇,3, 张文翠（1.广西无线宽带通信与信号处理重点实验室,桂林 541004；.桂林电子科技大学信息与通信学院,桂林 541004；3.桂林电子科技大学广西信息科学实验中心,桂林 541004）

瞬变电磁场模拟中的CPM L吸收边界条件

姜彦南1,2,3, 刘 文2, 王 娇2,3, 张文翠2
（1.广西无线宽带通信与信号处理重点实验室,桂林 541004；2.桂林电子科技大学信息与通信学院,桂林 541004；3.桂林电子科技大学广西信息科学实验中心,桂林 541004）

提出用于瞬变电磁法（TEM）模拟的时域有限差分（FDTD）算法中的卷积完全匹配层（CPML）吸收边界条件.首先,在磁场散度方程显式处理条件下,计算磁场z分量时,构造出一种计算时域卷积项的方法,并详细推导计算磁场z分量的表达式.而后,对均匀半空间模型进行数值计算.结果表明,提出的CPML吸收边界条件在保证计算精度的前提下,实现了瞬变电磁法时域有限差分高效正演计算.

瞬变电磁法；时域有限差分；完全匹配层；CPML吸收边界条件

0 引言

瞬变电磁法（Transient Electromagnetic Methods,TEM）是一种建立在人工可控源基础上的时间域电磁勘探方法[1－2],因其具有对低阻体反应灵敏、体积效应小、纵横向分辨率高、施工方便、效率高等优点,被广泛应用于金属矿勘探、煤矿水文地质调查和工程勘查等领域,是目前地质勘探中一种重要的方法.

随着计算机技术的发展,基于有限元、有限差分等数值计算的瞬变电磁法正演研究也得到了快速推进.在有限差分正演计算方面,国外具有代表性的研究主要有：Oristaglio和Hohmann[3]开创性地采用DuFort-Frankel有限差分法研究了二维地电断面下线源产生的瞬变电磁场；Wang和Hohmann[4－5]以地面均匀半空间瞬变电磁场的解析解为初始条件,采用改进的DuFort-Frankel有限差分形式研究了三维时间域正演算法；Commer和Newman[6－7]基于并行有限差分法研究了电偶源瞬变电磁三维正演算法.国内相关的研究开展稍晚,比如闫述[8]、刘云[9]等人利用DuFort-Frankel有限差分法分别采用总场和二次场求解法计算了二维瞬变电磁场,并对均匀半空间中异常体的瞬变电磁场分布特征进行了分析；孙怀凤等[10]将瞬变电磁激发源直接加入安培环路定理,并考虑一次场计算和关断时间的影响,采用时域有限差分（Finite Difference Time Domain,FDTD）法对三维模型进行了计算和分析.

由于计算机的局限性,基于有限差分的瞬变电磁数值模拟只能在有限区域内进行,这样必须对计算区域的边界进行截断处理.分析现有文献[3－10]发现,前人模拟瞬变电磁场过程中通常采用以下方式：假设计算区域足够大,使得地下三个截断边界离激励源和目标的距离足够远,此时地下目标扩散场在边界处满足Dirichlet条件,从而直接将边界值设为零.该方式的优点是边界条件设置简单、方便、可靠性高,且满足实际的物理规律；缺点是由于计算域范围足够大,数值正演计算时占用大量的计算内存,耗费大量的计算时间,导致基于有限差分的TEM计算效率极低.

为了克服以上缺点,在FDTD方法模拟瞬变电磁场时,我们采用缩小计算域范围,并在地下截断边界处设置合适吸收边界的形式加以实现.目前应用较多的吸收边界条件有Mur吸收边界条件、廖氏吸收边界条件和完全匹配层（Perfectly Matched Layer,PML）吸收边界条件.Mur吸收边界条件[11]虽然简单方便、占用内存小,但计算精度不高,在角区域存在较大误差；二阶近似的Mur吸收边界条件虽然精度有所改善,但对低频感应场的吸收效果差.廖氏吸收边界条件[12]能够很好地吸收来自计算区域的电磁波,但它的高阶吸收边界条件不稳定.PML边界条件[13－15]给吸收边界条件研究带来了本质性的突破,但它采用分裂电磁场的方式来描述各向异性材料,对计算机的硬件要求很高,并且在模拟瞬变电磁波时对地下高有耗介质中的波和倏逝波的吸收效果不佳.在PML基础上发展的UPML方法（uniaxial PML）[16,19]直接使用各向异性材料而不改变电磁场形式,能作为瞬变电磁波的吸收边界条件,但它的递推公式与材料特性有关,并且对大角度入射波及瞬变电磁波里低频成份的吸收效果差.目前最具潜力的当属卷积PML（Convolutional PML,CPML）吸收边界条件[20],它除了具有UPML吸收边界条件的性能外,还能对倏逝波、晚时反射波以及低频感应场进行有效的吸收,因而CPML吸收边界条件特别适合用做瞬变电磁法FDTD正演数值计算中截断边界的处理.

本文中,我们对CPML吸收边界条件进行研究,以用于瞬变电磁场时域有限差分算法计算区域的截断处理.

1 FDTD模拟TEM基本原理

准静态条件下,均匀、有耗、非磁性媒质中,无源Maxwell方程组为[4]

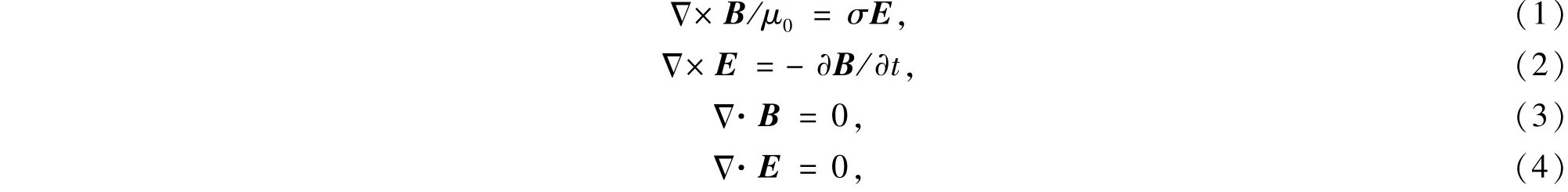
其中E为电场强度,B为磁感应强度,σ为电导率,μ0为真空中的磁导率.由于后期瞬变电磁场变化较缓慢, （1）式中忽略了位移电流项,缺少对电场的时间导数,因此方程组（1）～（4）式不能构成显式的时域有限差分方程,通常采用引入虚拟位移电流项的方式进行处理,则（1）式修改为

式中,γ具有介电系数的量纲,称为虚拟介电系数,其取值必须满足稳定性条件并且使引入的虚拟位移电流项不影响计算结果.

研究发现,在进行瞬变电磁场数值计算的过程中,公式（3）必须显式包含在迭代过程中,否则对低频电磁场的计算结果是错误的[4].因此,在下面章节中,我们将结合式（2）、（3）和（5）进行计算.对于磁场的计算,可采用先通过式（2）求解磁场x、y两个分量,然后再通过 Δ·B＝0求解磁场z分量的方式获得,即

在二维TMy模式下,只有Ey、Bx和Bz三个场分量,因此标量形式的Maxwell方程组为

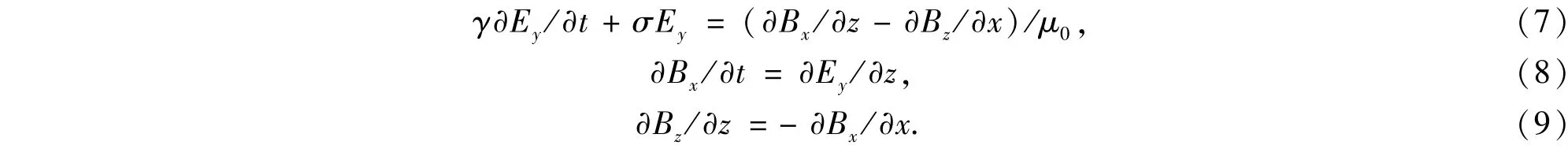
为了便于分析,采用均匀网格将以上三式进行FDTD离散.这里仅给出与式（9）对应的离散式

值得注意的是,（10）式中Bz的求解采用从模型的底边界向上步进到地－空边界的递推方式.

2 FDTD模拟TEM响应中的CPML吸收边界条件

由式（2）、（3）和（5）可知,频域中CPML区域内的约束方程组为

其中,算子 Δs定义为[21]

sx,sy,sz称为坐标拉伸因子,具有以下形式

其中,ε0为自由空间的介电常数,ω为角频率,σw是CPML区域内沿w方向的电导率,κw为网格延拓因子, αw是为改善对消逝波和低频波的吸收而引入的参数,它们分别为[21]

式中

其中εr为背景媒质的相对介电常数,δ为网格尺寸,ρ为各场分量到计算域与CPML交界面之间的距离,d 为CPML厚度,m和mα为多项式分布的阶数,σfactor为误差控制系数,σw,max、κw,max、αw,max分别为相应参数在w方向上的最大值.

定义傅里叶逆变换关系

由傅里叶变换理论及式（15）、（19）得[21]

其中f－1表示傅里叶逆变换算子,u（t）和δ（t）分别是阶跃函数和脉冲函数,t为时间.因此,在二维TMy模式下,应用于CPML区域的（11）式和（12）式转换成时域形式为[20]

式（21）、（22）的FDTD离散表达式可采用文献[22]的方法求得,而（13）式的CPML吸收边界条件公式在已掌握的文献中未见报道.下面重点推导对应于（13）式的CPML吸收边界条件.

将（14）式代入（13）式并展开得

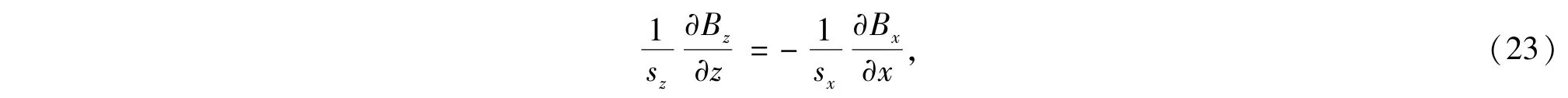
根据（20）式时－频域转换关系可得（23）式的时域形式为

考察（24）式不难发现,该式不仅左右两边都包含卷积项,而且卷积项形式为ζw（t）ƏBw/Əw,而CPML层中常规的方程表达式只有一边包含卷积项,且形式为ζv（t）ƏBw/Əv（如（21）,（22）式）,因此常规的FDTD离散方法无法求解（24）式.为此,针对（24）式中卷积项的计算构造如下：

将（25）式中x和z分量的时域卷积项分别代入（24）式两边,并采用中心差分离散得

整理后,即得

其中,

从（27）式可以看出,在处理CPML吸收边界时,磁场Bz的推导也是从底边界向上步进到地－空边界,这与计算域内磁场Bz计算过程完全一致.对比式（10）可以发现,（27）式中相对于常规FDTD迭代计算式多出了（1＋κxcx）κz/（1＋κzcz）κx和等号右边后两项.在非CPML区域的FDTD计算中所有对应的κw＝1以及σw＝0,从而cw＝0,（1＋κxcx）κz/（1＋κzcz）κx＝1,后两项为0.因此,可以把非CPML区域和CPML区域的场分量迭代公式合并为一式.

由以上分析可以看出,式（21）,（22）和（24）就构成了二维TMy模式下瞬变电磁法FDTD计算的CPML吸收边界条件.

3 算例验证及分析

图1 CPML吸收边界条件截断的均匀半空间模型Fig.1 Sketch of homogeneous half-space model truncated by CPML ABC

为了验证分析本文提出的CPML吸收边界条件的有效性及可靠性,考虑如图1所示的均匀、有耗、非磁性二维半空间模型.坐标原点位于地表面上,水平方向为x轴,垂直向下为z轴正方向.空间步长Δx＝Δz＝10 m,FDTD计算区域为60×30个网格.地下介质电导率σg＝1/300（s·m－1）.在x＝－100 m和x＝100 m的地面上（z＝0）分别通以I1＝1 A和I2＝－1 A的无限长线电流源s1和s2.t＝0时刻断开电流,初始时刻t0＝1.047 2μs；时间步长Δtn＝a,虚拟介电常数γ ＝D/μ0（Δtn/δ）2,其中a为控制系数,D为模拟空间的维度,δ为空间步长,n为时间步数,取值分别为a＝0.2,D＝2,δ＝10m,n＝0,1,2,…, Δtn和γ随时间延迟而逐渐增大；源作为初始条件加入[3],在t＝t0时刻赋给电场初始值,t＝t0＋Δt0/2赋给磁场初始值.地－空边界采用地面上的垂直磁场Bz向空气层延拓半个网格的切向磁场Bx得到（如图1中Γ0所示）,地下三个边界则采用CPML吸收边界条件处理.

为了获得较好的CPML吸收性能,基于大量数值试验并考虑计算量问题,最终选择（16）－（18）式中的参数如下：κmax＝6,αmax＝0.05,σfactor＝300,m ＝1,mα＝1,CPML的厚度d为12个网格.设置观察点A、B、C距离CPML区域内边界仅一个网格,分别位于网格点（－29,1）、（－29,15）和（－29,29）处,用于定量分析CPML的处理效果.本节均基于此例进行分析.

3.1 计算结果正确性分析

线电流源在地下均匀半空间的辐射场为向下、向外扩散的“烟圈”.图2给出了两个不同时刻的电场Ey等值线图.从图中可以看出,在截断边界处,“烟圈”呈规则的形状,表明本文提出的CPML吸收边界具有良好的外向行波吸收性能.

图2 不同时刻电场Ey等值线图Fig.2 Contours of electric field Eyat different times

图3 坐标原点电动势衰减曲线Fig.3 Decay curves of EMF at origin of coordinate

图3给出了坐标原点处垂直感应电动势（Electromotive force,EMF.垂直感应电动势定义为垂直磁感应强度对时间的一阶导数,即 EMF ＝ƏBz/Ət＝－ƏEy/Əx）衰减曲线,其包括以下三种情况的计算结果：①解析解；②计算域足够大,地下截断边界采用Dirichlet条件的数值解,即传统的FDTD数值解；③计算域缩小至60×30个网格,地下截断边界采用CPML处理的FDTD数值解.由图可看出,三种情况下的计算结果具有很好的一致性,表明本文提出的算法和编写的计算程序是正确的.

3.2 计算结果误差分析

为定量分析本文提出的CPML吸收边界性能,定义相对反射误差值（dB）为[20]

其中,ξ代表观察点处的测试值,ξref代表观察点处ξ的参考值,ξref,max代表观察点处ξ的参考值在整个数值模拟时间内的最大值.

1）不同位置处的电场相对反射误差分析

图4是在CPML吸收边界条件下,程序运行1 000个时间步迭代至1.1 ms,在A、B、C观察点处计算得到的电场相对反射误差曲线.其中,参考值采用传统的FDTD方法获得.由于（30）式中参考值最大值随着深度增大而减小,因此随着深度的增加相对反射误差逐渐增大,但最大误差仅为－35 dB.结果表明本文提出的CPML吸收边界处理后的数值计算实现了较高的计算精度.

2）CPML层数不同时的电场相对反射误差分析

图5给出了CPML层分别为10、15和20个元胞时,观察点B处的电场相对反射误差曲线.其中,参考值同样采用传统的FDTD方法获得.从图中可以看出,随着CPML层数的增加,吸收效果逐渐改善.考虑内存资源和计算时间等因素,CPML层数可在10～15之间选择.

3）不同数值解下的地表感应电动势相对反射误差分析

为了进一步分析本文提出的CPML吸收边界的效果,我们采用“伪FDTD方法”计算垂直感应电动势.（令图1所示的模型不含CPML吸收层,直接将边界处的场值设为零,而后采用传统FDTD方法进行计算.但此时不满足计算区域足够大的条件,故为了描述需要称其为“伪FDTD方法”）.

图4 观察点A、B、C处的相对误差Fig.4 Relative errors at points A,B and C

图5 B处不同CPML层数的相对误差Fig.5 Relative errors of CPML with different layer number at point B

图6 不同数值解下的地表感应电动势相对误差Fig.6 Relative errors of EMF at the surface under different numerical solution

地表x＝290 m处垂直感应电动势的三种数值解相对反射误差如图6所示（其中,参考值采用解析解）.可以看出,伪FDTD方法数值解的相对反射误差大于0dB,在截断边界处产生了很大的反射；而采用CPML吸收边界条件处理后,相对反射误差大幅度减少,在截断边界处几乎不产生反射,达到了与传统FDTD数值计算接近的计算精度.结果表明本文提出的CPML吸收边界具有很好的吸收效果.

3.3 计算资源占用及计算效率分析

对于二维TMy模式,电磁场只有三个分量,设各场分量采用双精度型变量（每个变量占内存8个Bytes）,FDTD区域内元胞总数为N.如果在目标建模时不直接给出每个元胞电磁参数,而是给出每种介质的介质编号,则识别各个场分量离散位置处的介质参数需要1个字节的整数.如果每个网格各场分量有相同的介质参数,则有[22]：

根据（31）式,在图1模型中未引入CPML吸收边界条件且计算域足够大的情况下,设其网格数为800× 400,则计算三个场量需要内存7.63 MB,运行1 000步耗时55.6秒.而引入CPML吸收边界条件后,总网格数降为84×42,即使在完全匹配层内因处理CPML吸收边界条件而引入了ψ变量,计算三个场量所需内存也仅为0.12 MB,运行1 000步耗时0.79秒.可以看出,本文提出的CPML吸收边界条件可以有效地节省计算内存,大幅缩短计算时间,明显提高数值计算效率,这使得基于FDTD正演计算的TEM快速反演成为可能.

4 结论

在瞬变电磁法的传统FDTD正演计算中,因截断边界要求足够远,导致模拟区域范围广、数值计算量大、迭代时间长、计算效率低等问题.本文提出的应用于瞬变电磁法FDTD正演计算的CPML吸收边界条件不仅保证了FDTD数值计算的精度,而且克服了传统FDTD正演计算的缺点.

本文方法可进一步推广到三维情形,以用于地下三维目标TEM响应的FDTD正演计算.

[1] Niu Z L.The theory of time-domain electromagnetic methods[M].Changsha：Central South University of Technology Press, 1992：1.

[2] Nabighian M N.Quasi-static transient response of a conducting half-space—An approximate representation[J].Geophysics, 1979,44（10）：1700－1705.

[3] Oristaglio M L,Hohmann GW.Diffusion of electromagnetic fields in two-dimensional earth：a finite difference approach[J].Geophysics,1984,47（7）：870－894.

[4] Wang T,Hohmann W G.A finite-difference,time-domain solution for three-dimensional electromagnetic modeling[J].Geophysics,1993,58（6）：797－809.

[5] Wang T,Tripp A C,Hohmann GW.Studying the TEM response of a 3-D conductor at a geological contact using the FDTD method[J].Geophysics,1995,60（4）：1265－1269.

[6] Newman G A,Commer M.New advances in three-dimensional transient electromagnetic inversion[J].Geophys J Int,2005, 160（1）：5－32.

[7] Commer M,Newman G.A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources [J].Geophysics,2004,69（5）：1192－1202.

[8] Yan S,Chen M S,Fu JM.Direct time-domain numericalanalysis of transientelectromagnetic fields[J].Chinese JGeophys, 2002,45（2）：275－284.

[9] Liu Y,Wang X B,Wang Y.Numericalmodeling of the 2D time-domain transient electromagnetic secondary field of the line source of the current excitation[J].Applied Geophysics,2013,10（2）：134－144.

[10] Sun H F,LiX,LiSC,etal.Three-dimensional FDTDmodeling of TEM excited by a loop source considering ramp time[J].Chinese JGeophys,2013,56（3）：1049－1064.

[11] Mur G.Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations[J].IEEE Trans Electromagn Compat,1981,23（4）：377－382.

[12] Liao Z P,Huang K L,Yang B P,etal.A transmitting boundary for transientwave analyses[J].Scientia Sinica（Series A）, 1984,27（10）：1062－1076.

[13] Berenger JP.A perfectlymatched layermedium for the absorption of electromagnetic waves[J].JComput Phys,1994,114：185－200.

[14] Berenger JP.Perfectlymatched layer for the FDTD solution ofwave-structure interaction problem[J].IEEE Trans Antennas Propagat,1996,44（1）：110－117.

[15] Zheng Z,Yang L.3D modified novel PML absorbing boundary condition for truncating magnetized plasma[J].Chinese J Comput Phys,2013,30（6）：895－901.

[16] Sacks Z S,Kingsland D M,Lee D M.A perfectly matched anisotropic absorber for use as an absorbing boundary condition [J].IEEE Trans Antennas Propagat,1995,43（12）：1406－1463.

[17] Gedney SD.An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices[J].IEEE Trans Antennas Propagat,1996,44（12）：1630－1639.

[18] Chai Y,Sun J,Li L,etal.Unifiedmodeling and optimization of UPML absorbing boundary conditions[J].Chinese JComput Phys,2011,28（3）：413－419.

[19] Yang T C,Li H,Zhang H.Forward modeling of GPML absorbing boundary conditions in GPR simulation[J].Chinese J Comput Phys,2014,31（2）：200－206.

[20] Roden JA,Gedney SD.Convolution PML（CPML）：an efficient FDTD implementation of CFS-PML for arbitrarymedia[J].Microwave Opt Tech Lett,2000,27（12）：334－339.

[21] Taflove A,Hagness SC.Computational electro-dynamics：The finite-difference time-domain method[M].Norwood,Artech House,2005：289－310.

[22] Ge D B,Yan Y B.Finite difference time domain method of electromagnetic wave（3rd edition）[M].Xi’an：Xidian University Press,2011：206－207.

CPM L Absorbing Boundary Condition in M odeling of Transient Electromagnetic Fields

JIANG Yannan1,2,3, LIUWen2, WANG Jiao2,3, ZHANGWencui2
（1.Guangxi Key Laboratory ofWirelessWideband Communication＆Signal Processing,Guilin 541004,China；
2.School of Information and Communication Engineering,Guilin University ofElectronic Technology,Guilin 541004,China；
3.Guangxi Experiment Center of Information Science,Guilin University of Electronic Technology,Guilin 541004,China）

A scheme of convolutional perfectly matched layer（CPML）absorbing boundary condition（ABC）is proposed,which is used to truncate finite-difference time-domain（FDTD）method modeling transient electromagnetic（TEM）response.It derives specially CPML formulation dealing explicitly with divergence of magnetic induction and conceives an algorithm calculating convolutional term of z component.Then,the scheme is validated by numerical modeling of a homogeneous half-space model.The results indicate that efficient calculation of TEM is achieved.

transient electromagneticmethod；finite-difference time-domain；perfectlymatched layer；convolutional PML absorbing boundary condition

1001-246X（2015）06-0701-08

P631

A

2014－11－21；

2015－02－09

国家自然科学基金（61001020）、广西自然科学基金（2014GXNSFAA118283）、广西研究生教育创新计划（GDYCS201415）和广西信息科学实验中心资助项目

姜彦南（1980－）,男,博士,副教授,主要从事电磁场数值计算、电磁辐射与散射研究,E-mail：ynjiang＠guet.edu.cn