钢铝结构连接耦合损耗因子计算方法研究
第一作者林永水男,博士生,1983年11月生
通信作者吴卫国男,教授,1960年2月生
钢铝结构连接耦合损耗因子计算方法研究
林永水, 吴卫国, 陈景昊, 周雍, 周超
(武汉理工大学交通学院,武汉430063)
摘要:统计能量法已广泛用于解决高频振动与噪声问题,耦合损耗因子是其关键参数之一。研究基于统计能量法、有限元法和功率输入法,提出一种钢铝连接耦合损耗因子数值计算方法,并运用MATLAB编写了计算软件。通过对含过渡接头的T型连接结构进行数值和实验研究,验证了该法的可靠性。这对提高钢铝混合结构的噪声预报精度及指导其结构声学设计具有重要意义。
关键词:统计能量法;有限元法;功率输入法;耦合损耗因子;钢铝过渡接头
收稿日期:2013-11-08修改稿收到日期:2014-04-21
中图分类号:U663;U668文献标志码:A
A new calculating method for coupling loss factor of a steel-aluminum junction
LINYong-shui,WUWei-guo,CHENJing-hao,ZHOUYong,ZHOUChao(School of Transportation, Wuhan University of Technology, Wuhan 430063, China)
Abstract:Statistical energy analysis (SEA) becomes a useful technique for providing a solution to high frequency noise and vibration. Coupling loss factor (CLF) is one of important parameters of SEA. Based on SEA, finite element analysis (FEA) and power injection method, a numerical calculation method of CLF for a steel-aluminum junction and a simulation program with MATLAB were proposed here. A T-shaped plate structure connected by a steel-aluminum transition junction was investigated with numerical simulation and tests. The results verified the reliability of the proposed method, and they provided a reference for improving the accuracy of noise prediction of steel-aluminum jnctions and their structural and acoustic design.
Key words:statistical energy analysis (SEA); finite element analysis (FEA); power injection method (PIM); coupling loss factor (CLF); steel-aluminum transition junction
统计能量法是分析高频振动噪声问题的重要方法,广泛应用于工程领域[1-2],其关键参数有输入功率、模态密度、耦合损耗因子和内损耗因子。耦合损耗因子反映各子系统之间的能量传递关系,国内外对其开展了大量的研究。文献[3-6]基于波分析法对耦合损耗因子进行了深入研究,文献[7-10]运用有限元法对耦合损耗因子进行了探讨性研究。卢兆刚等[11]采用能量有限元法对中低频耦合损耗因子进行了研究。
一些船舶为了减轻重量,主船体采用钢制结构,上层建筑采用铝合金结构,两者由过渡接头连接[12-15],如图1所示。过渡接头的存在会影响结构声波和振动能量的传递,此时,计算钢铝连接耦合损耗因子时须考虑过渡接头的影响。目前国内外对有过渡接头的异种材料结构连接的耦合损耗因子的研究较少,没有给出较为可靠的计算方法。研究针对钢铝连接耦合损耗因子开展研究,提出数值计算方法,并进行了实验验证。

图1 常用钢-铝过渡接头及其连接形式 Fig.1 Common types of steel-aluminum transition junction and connection forms
1理论分析
1.1统计能量分析法(SEA)
根据能量守恒原理,子系统消耗的能量加上传递给其它子系统的能量,应等于输入给该子系统的能量,对于具有N个子系统的系统,其能量平衡方程为:
(1)
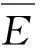
1.2频率响应分析
对简谐激励下有阻尼强迫振动,运动方程为:
(2)

本文选用模态法来求解频率响应,物理坐标与模态坐标转换关系如下:
{u}={φ}{ξ(ω)}eiωt
(3)
在模态坐标系下,结构动力学基本运动方程变成:
[-ω2[φ]T[M][φ]+iω[φ]T[C][φ]+
[φ]T[K][φ]]{ξ(ω)}=[φ]T{F(ω)}
(4)
如果阻尼分别加到每一个模态上情况下,解耦后,可以得到每一个模态下运动方程:
-ω2miξi(ω)+iωciξi(ω)+kiξi(ω)=Fi(ω)
(5)
每一个模态下的响应由下式计算
(6)
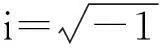
1.3输入功率
激励在任意角频率的输入功率,可根据下式计算:
(7)
其中:F*(ω)为激励力的复共轭;ν(ω)为激励点速度;Re为取实部。
1.4子系统振动能量
当输入激励作用在子系统某一节点上,每一子系统总振动能量是其动能的两倍,因此子系统总能量为:
(8)
其中:m为子系统的质量,N为子系统的总节点数。
1.53子系统耦合损耗因子计算
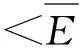
(9a)
上式左边乘以能量矩阵的逆,可得损耗因子矩阵
(9b)
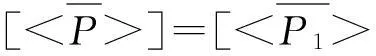

(9c)
2钢铝连接耦合损耗因子数值分析
2.1基于MATLAB的耦合损耗因子数值计算流程
根据功率输入法求耦合损耗因子的思路来进行仿真分析,具体的计算流程见图2。

图2 过渡接头耦合损耗因子数值计算流程 Fig.2 The program plan of calculation of the coupling loss factor
首先建立结构有限元模型,生成*.bdf文件,然后MATLAB调用NASTRAN进行模态频响分析,输出*.punch结果文件,调用数据提取M文件,得到所有节点的速度响应,继续调用数据分析M文件,计算各个子系统在初始中心频率下频带和空间平均输入功率和振动能量。MATLAB修改上一个*.bdf文件(激励作用的节点号,计算步长,求解频域的上下限等),重复以上步骤,直到截止中心频率。MATLAB程序求解式(9b),得三分之一倍频程的耦合损耗因子。以上计算由程序自动完成,6个激励点的计算耗时约2 h。
2.2分析模型参数
2.2.1模型物理参数
将T型钢铝结构划分为3个子系统,其中两块钢板分别为子系统1和子系统2,铝板为子系统3,如图3所示。模型的参数具体取值具体见表1。
2.2.2有限元模型网格尺寸
网格尺寸一般不大于所涉及的最大模态频率波长
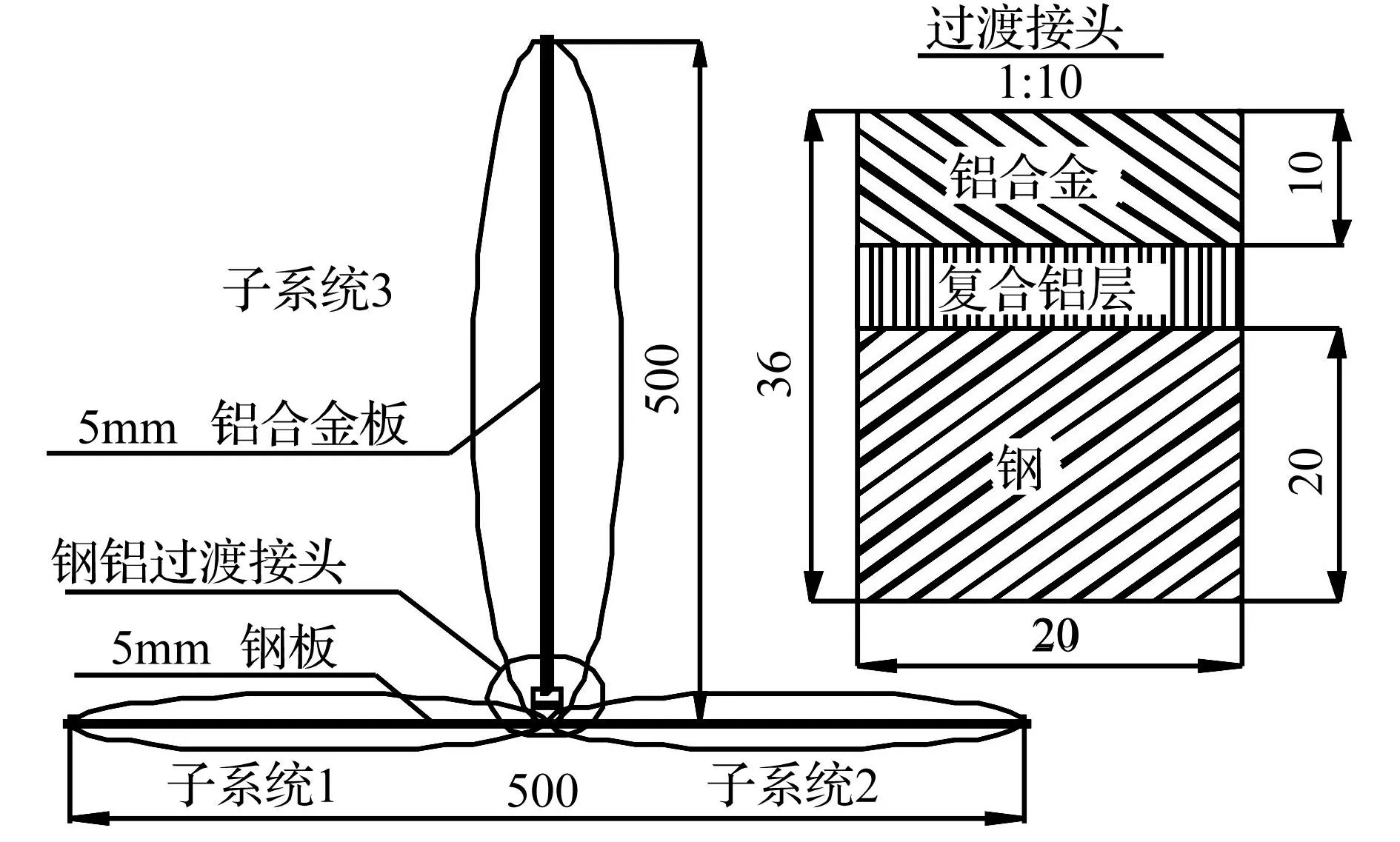
图3 分析模型及其参数 Fig.3 The analysis model and its parameters

系统编号材质结构尺寸/mm弹性模量/Mpa泊松比密度×103/(kg·m-3)123钢钢铝500×250×6500×250×6500×500×52.1×10112.1×10117.0×10100.30.30.337.857.852.80
的1/6,即板中弯曲波波长的1/6[16],具体按下式计算。
(10)
其中:E表示弹性模量;μ为泊松比;h为板厚;ρ为材料密度;f为频率,Hz。
根据本文的计算频率上限值,按照式(10)可得系统1和系统2所要求的网格尺寸不大于19mm,系统3所要求的网格尺寸不大于17mm,综合考虑,3个子系统的单元的网格尺寸取10mm。
2.3模型模态频率响应分析
模态频率响应分析中各个中心频率下的计算频域和计算步数见表2。
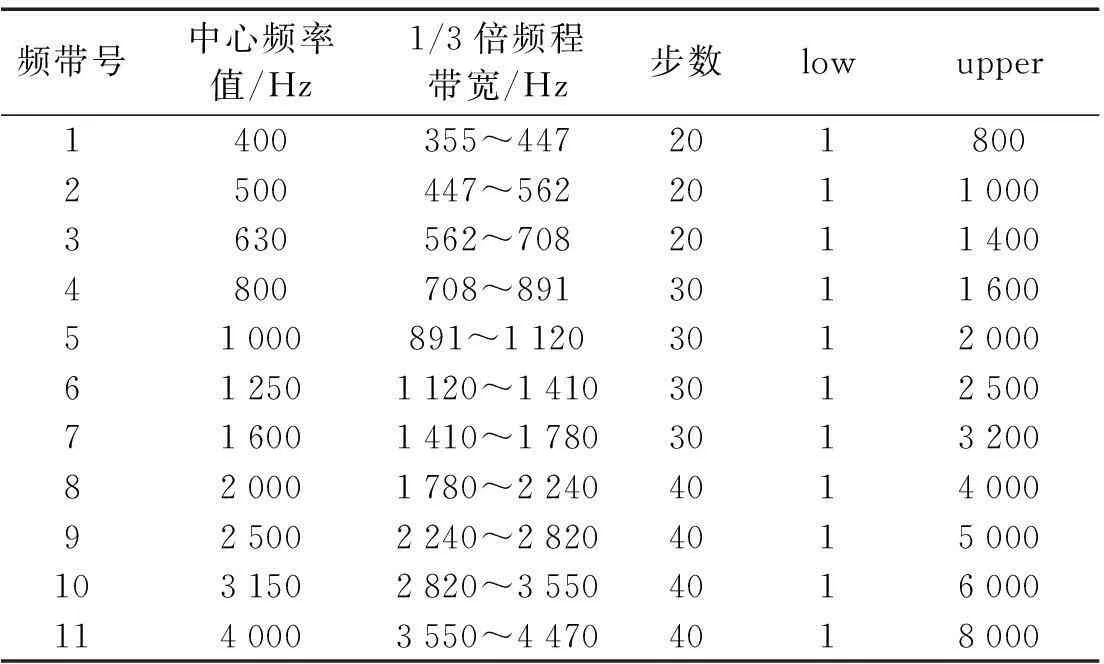
表2 计算步长和截止频率(1/3倍频程)

图4 不同模态阻尼系数的η 12计算结果对比 Fig.4 The comparison of η 12 for different modal damping factors
图4给出了模态阻尼系数分别为0.01、0.03以及0.05时系统1到系统2的耦合损耗因子的计算值。比较发现,模态阻尼系数对耦合损耗因子的计算值有一定影响。根据文献[7]及图4,文中以下的仿真计算模态阻尼系数均取0.03。
2.4 随机激励点数目
为了验证方程(9a)的稳定性,图5给出了三个激励点(P3)、六个激励点(P6)以及九个激励点(P9)作用下,各中心频率对应的矩阵(9c)的条件数。
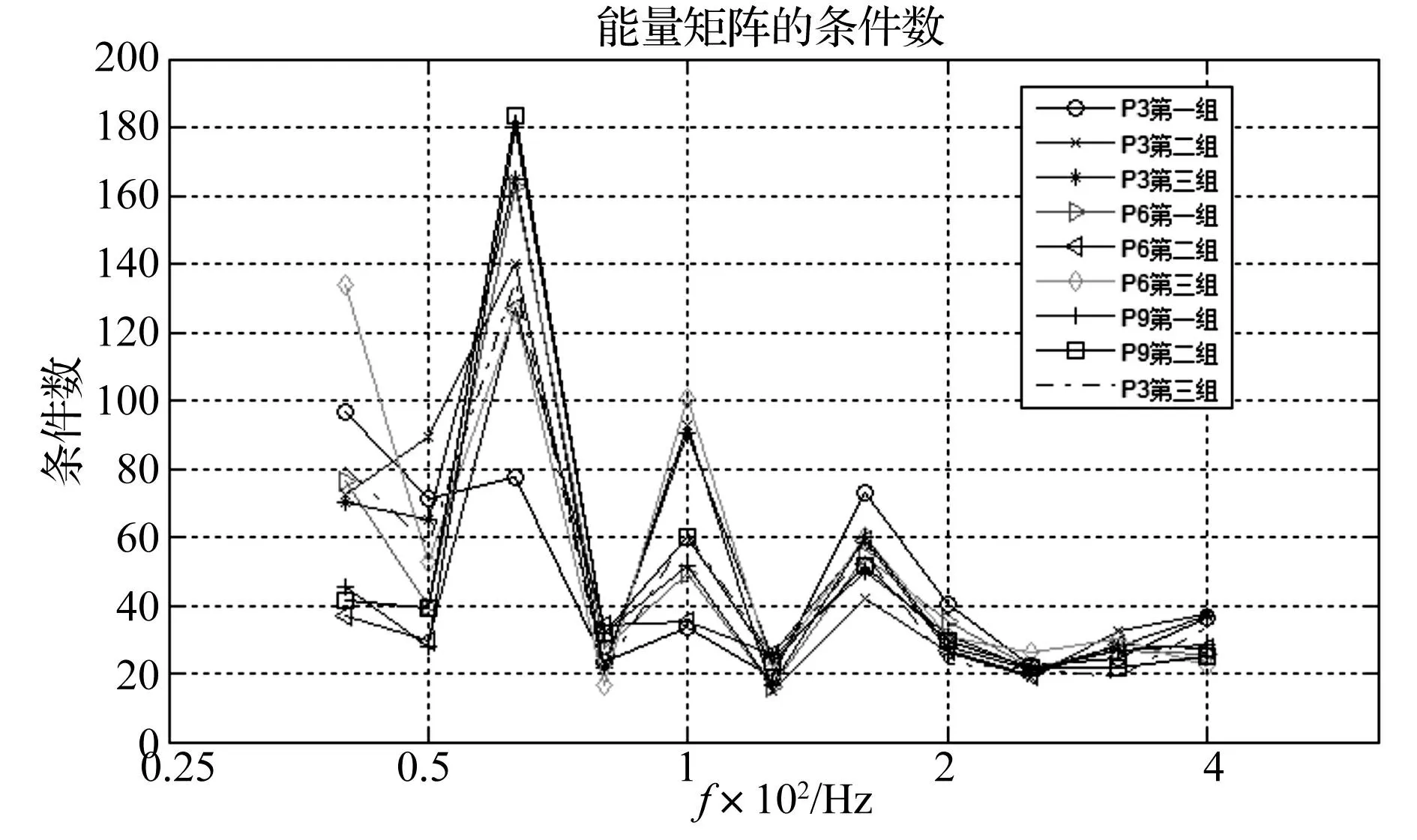
图5 P3,P6以及P9作用下的矩阵条件数 (三分之一倍频程) Fig.5 Matrix condition numbers under different groups (1/3 octave)
运用SPSS数据分析软件进行独立样本T检验,附表1和2分别给出了中心频率为1600Hz时,3个激励点与9个激励点以及6个激励点与9个激励点作用下系统能量比的分析结果(95%置信度),认为其均值不具有显著性差异,而对于方差,P3组计算的偏差值明显较大,P6组和P9组差别在可接受范围以内。综合考虑计算精度和效率,取六个随机激励点较为合适。
2.5数值仿真结果及分析

图6 无过渡接头耦合损耗因子波动法 和有限元法计算数值比较 Fig.6 Comparison of CLFs obtained from WA and FEM for the connection without transition junction
图6给出了无过渡接头T型连接耦合损耗因子波动法和本文计算方法的计算结果,对应的耦合损耗因子在高频段吻合得较好。图7给出了有无接头两种模型的耦合损耗因子有限元计算结果,揭示过渡接头会影响耦合损耗因子的计算值。比较可以得到,过渡接头的会使钢板-钢板的耦合损耗因子(CLF12或者CLF21)降低,钢板-铝板的耦合损耗因子(CLF13)会增大。由此可知,传统的耦合因子计算方法已经不适用于含过渡接头的结构连接耦合损耗因子计算。
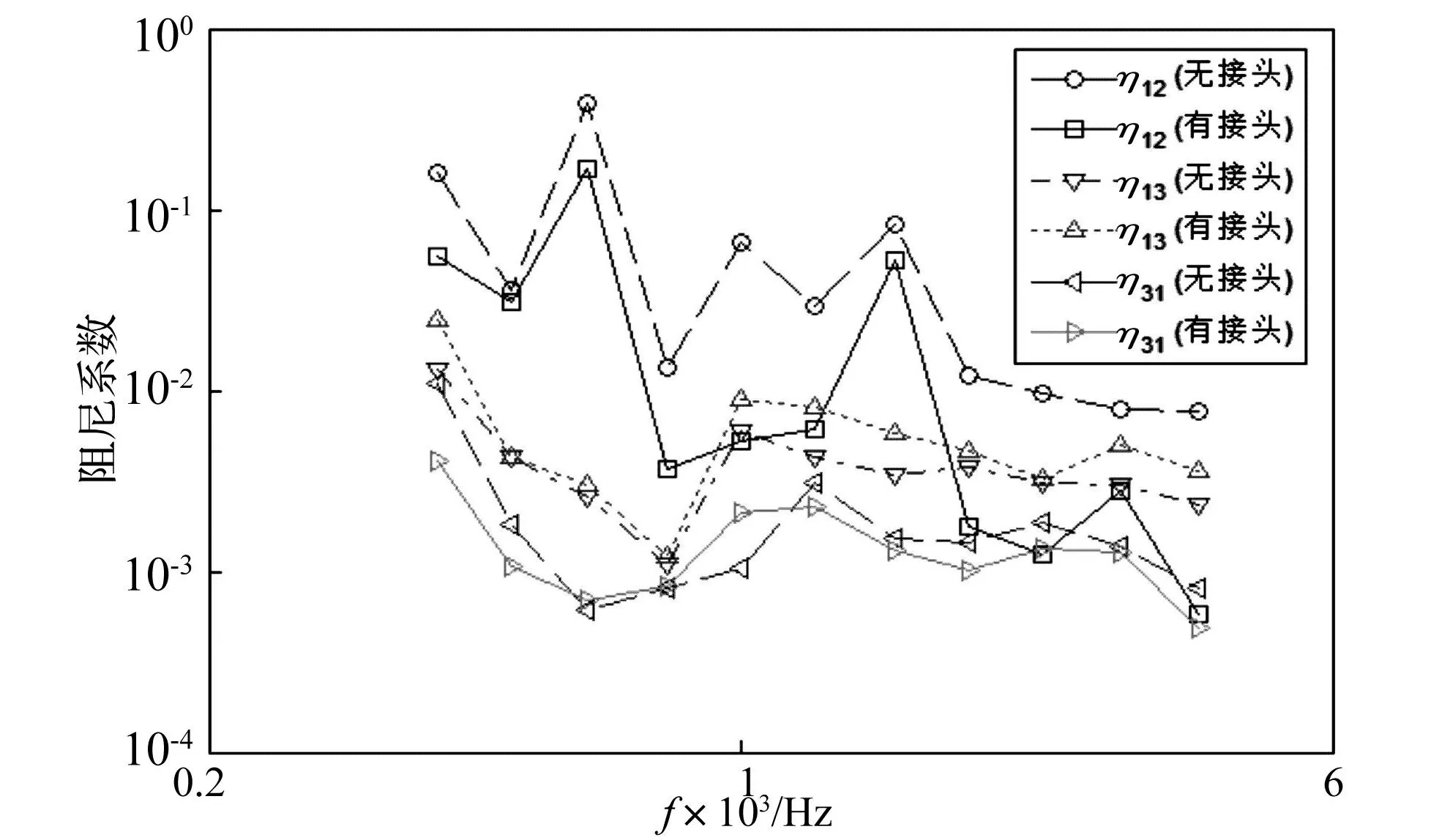
图7 不同连接形式耦合损耗因子有限元法计算数值比较 Fig.7 Comparison of CLFs for different junctions by FEM
3耦合损耗因子实验研究
3.1实验方法(PIM)
本实验采用功率输入法(PIM)作为结构连接耦合损耗因子的测量方法[18-20]。测试激励的输入功率和子系统的能量,其计算按照下式:
(11)
(12)
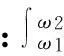
3.2测点布置与边界条件
测量时,将试件悬挂,确保满足自由边界条件以减小外界影响。同时为了保证满足空间平均的要求,在输入点和响应点布置时要体现随机性,同时要求至少3个输入点和6个响应点。具体布置如图8所示。
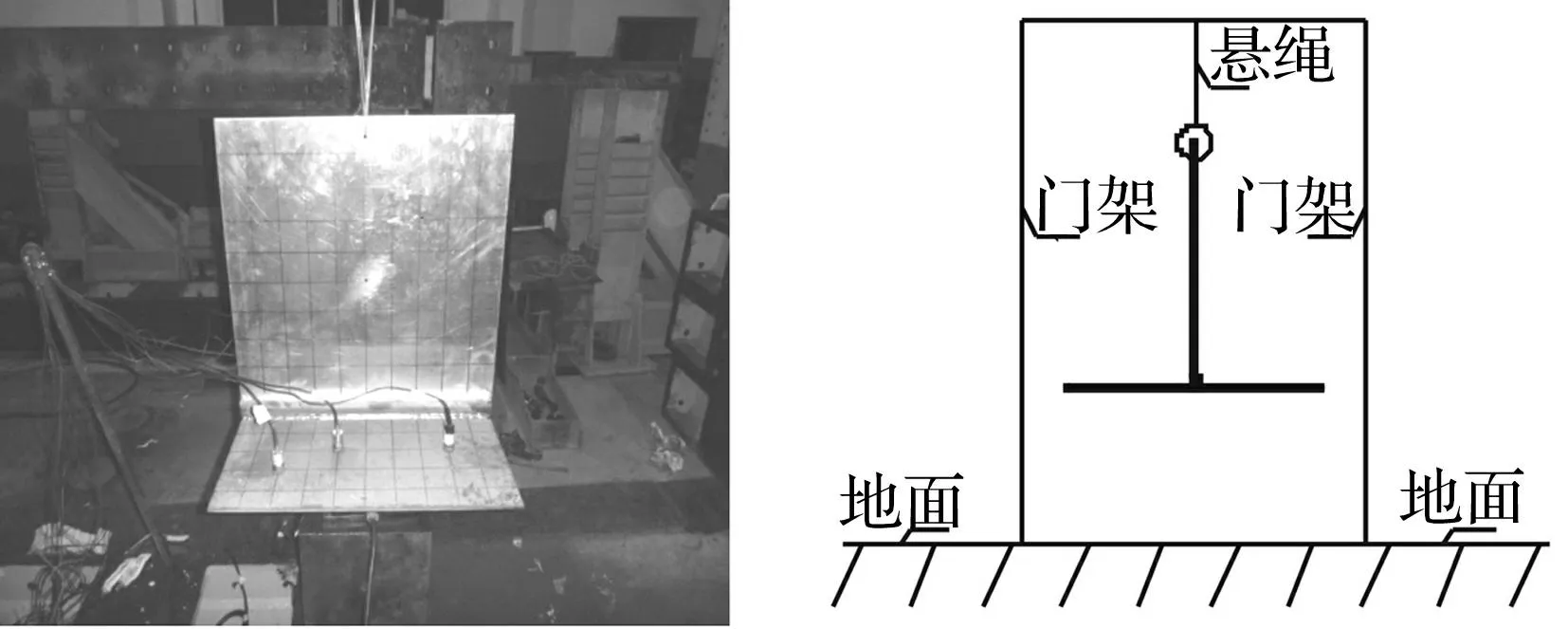
图8 实验模型及其悬挂方式 Fig.8 The experimental model and its suspension way
3.3测量与数据分析系统
激励力是由Bruel and Kjaer shaker model 4809施加的0~6400Hz范围内的随机振动激励。激励点的输入力和加速度信号通过与激振器相连的阻抗头测量。激励力的大小通过信号放大器控制。所有加速度输出响应信号由压电式加速度传感器KD1010L测量。力和加速度传感器采集获得的随机信号送到Bruel & Kjaer PULSE Lab Shop测试系统,给出力和加速度的互功率谱和响应点的加速度自功率谱。整个实验系统见图9。
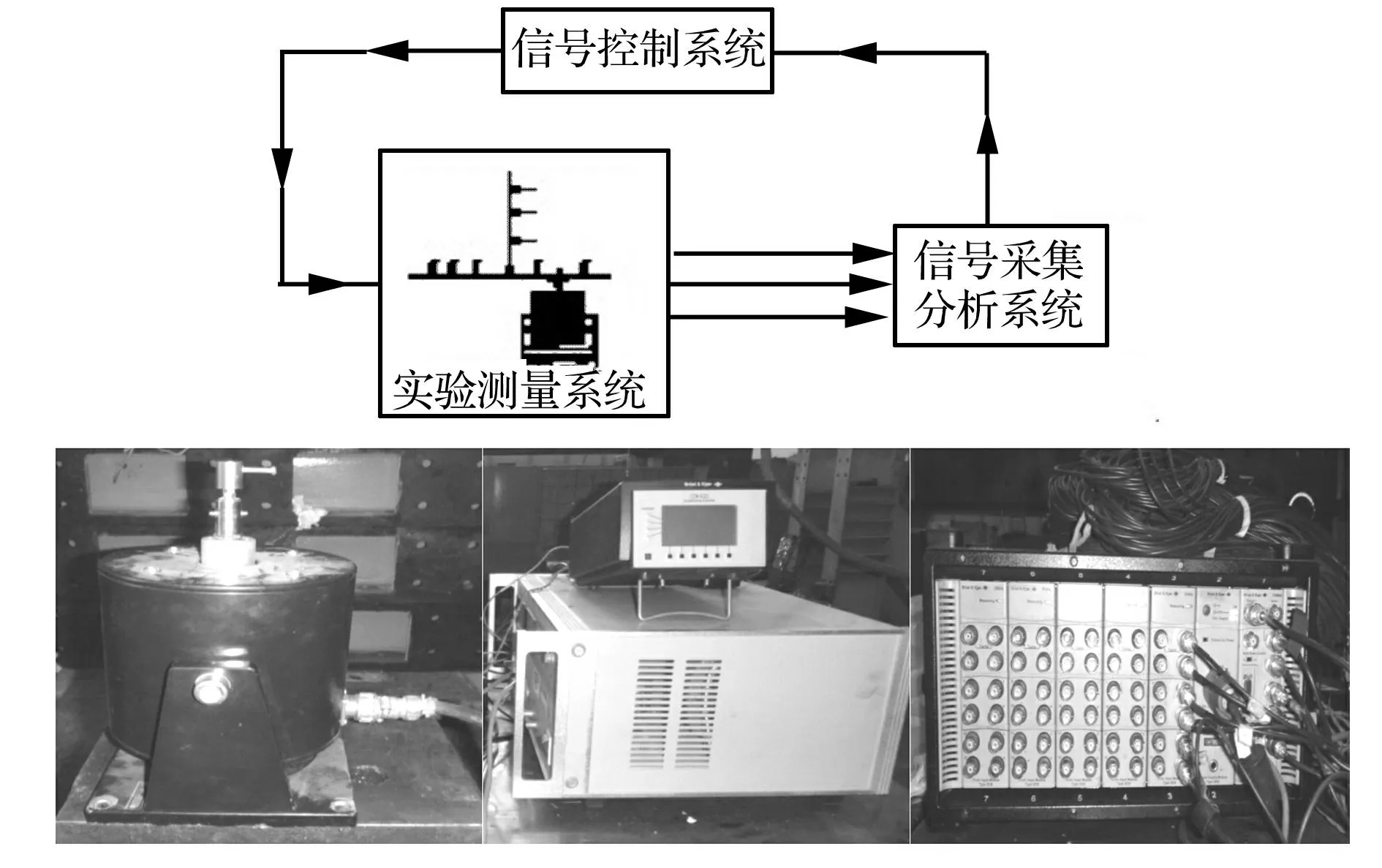
图9 实验装置及仪器 Fig.9 Experimental setup and facilities
3.4测量结果与误差分析
导致实验出现误差的主要因素有:实验很难模拟自由边界条件,测试时很难反映有限物体的边界近场影响,包括结构声产生透射、反射等。测量铝板系统的振动加速度的传感器需要用强力胶水粘贴铁片,由于胶水和铁片的衰减,也会造成一定的信号测量误差。由于测点数目以及测点布置,难以完全表征板的振动统计特性,这些因素均会导致实验结果偏离真实值。
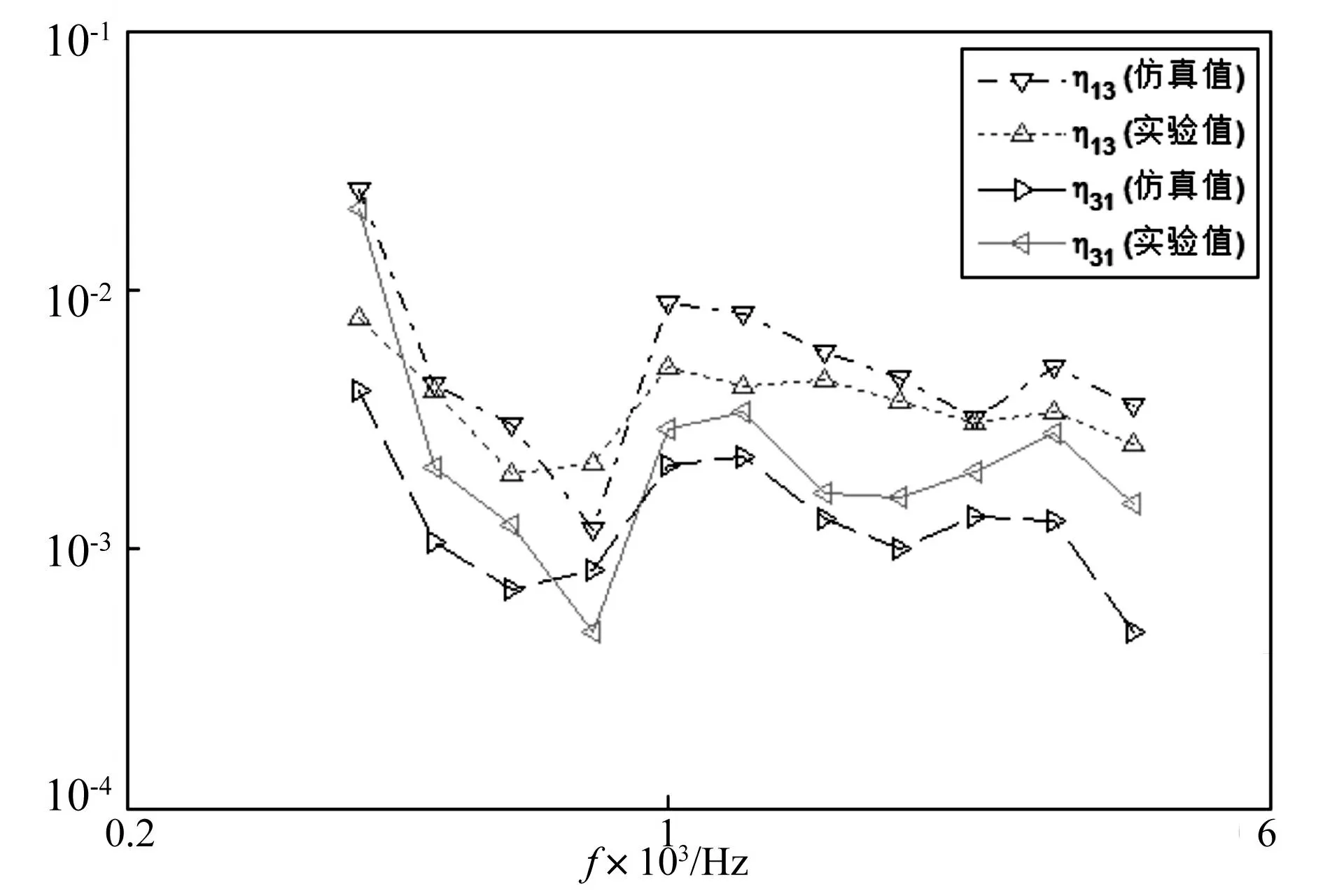
图10 耦合损耗因子仿真值和实验功率输入法计算值比较 Fig.10 Comparison of CLFs for the junction obtained from simulation and experimental PIM
T型连接耦合损耗因子数值计算与实验测得的结果相比较(图10),在中低频段两者偏差较大;在高频段,两者吻合较好。主要其原因有:在中低频段,频带内的振型数较少,模态重叠因子较小,SEA能量流平衡方程此时有一定的局限性,导致仿真结果出现偏差,仿真时模态阻尼系数、网格尺寸以及激励点数目及位置的取值对计算结果也会产生影响。
4结论
对工程中异种材料连接复杂结构,通常的计算方法忽略了过渡接头的影响。为此,探讨带有过渡接头的钢铝混合结构连接的耦合损耗因子计算方法,并编写了计算软件,通过与实验结果对比,验证了本文提出的CLF数值计算方法的可靠性,这对提高混合结构噪声的SEA预报精度具有重要意义。目前本方法耗时较大,中低频段的计算精度不是很理想,因此提高计算效率和精度将是下一步要开展的重要工作。另外目前研究只考虑了各子系统之间弯曲波的能量传递,下一步工作应探讨各子系统之间波型转换对耦合损耗因子计算结果的影响。
参考文献
[1]Lyon R H, DeJong R G. Theory and application of statistical energy analysis [M]. London: Butterworth-Heinemann, 1995.
[2]姚德源,杨福家,王其政.统计能量分析原理及其应用[M]. 北京: 北京工业大学出版社,1995.
[3]Yap F F, Woodhouse J. Investigation of damping effects on statistical energy analysis of coupled structures [J]. Journal of Sound and Vibration 1996, 197:351-371.
[4]Tso Y K. An Investigation of the coupling loss factor for A cylinder/plate structure [J]. Journal of Sound and Vibration,1997, 199(4):629-643.
[5]Tso Y K. The transmission of vibration through a coupled periodic structure [J]. Journal of Sound and Vibration, 1998, 215(1):63-79.
[6]王宏伟,赵德有.平板与周期加筋阻尼板间耦合损耗因子的研究[J].船舶力学,2001,5(2) :55-61.
WANG Hong-wei,ZHAO De-you. Study on coupling loss factor between uniform plate and periodic stiffened damping plate [J]. Journal of Ship Mechanics,2001,5(2):55-61.
[7]Stell J A, Craik R J M. Statistical energy analysis of structure-borne sound transmission by finite-element methods [J]. Journal of Sound and Vibration, 1994, 178:553-561.
[8]Fredo C R. A SEA-like approach for the derivation of energy flow coefficients with a finite element model [J]. Journal of Sound and Vibration, 1997, 199:645-666.
[9]Yan H, Parrett A, Nack W. Statistical energy analysis by finite elements for middle frequency vibration [J].Journal of Sound and Vibration, 2000, 35: 297-304.
[10]Thite A N, Mace B R. Robust estimation of coupling loss factors from finite element analysis [J].Journal of Sound and Vibration,2007,303:814-831.
[11]卢兆刚,郝志勇,郑旭.基于有限元能量流模型的复杂耦合结构中低频段耦合损耗因子的计算[J].振动与冲击,2011,30(11): 42-46.
LU Zhao-gang, HAO Zhi-yong, ZHENG Xu. Coupling loss factor calculation of complex coupling structure based on finite element energy flow model[J].Journal of Sound and Shock,2011,30(11):42-46.
[12]王承权,张京立.舰船钢-铝结构过渡接头的应用及节点设计[J].船舶工程,2004,26(06):34-38.
WANG Cheng-quan, ZHAN Jing-li. Application and nodal point design of structural transition joint in Ship with steel-aluminum superstructure[J].Ship Engineering, 2004, 26(6):34-38.
[13]王承权,夏炳仁.铝合金上层建筑与钢主船体的新型焊接过渡接头[J].船舶工程,1999(4):26-28+34-3.
WANG Cheng-quan,XIA bing-ren. A new type of transition Joints for welding of aluminum alloy superstructure to steel hull structure [J].Ship Engineering,1999 (4): 26-28+34-3.
[14]许芝芳,于长亮.铝-钢过渡接头在船舶结构焊接中的应用[J].中国水运(下半月),2008(6):156-157.
XU Zhi-fang,YU Chang-liang. The application of aluminum- steel transition joints in Ship structure welding[J].China Water Transport,2008(6):156-157.
[15]John Banker, Job Visser. 铝-钢连接[J]. 造船师(中文版),2008( 9): 238-239.
John Banker, Job Visser. Aluminum-steel junction [J].Ship builder, 2008(9): 238-239.
[16]Vigran, Tor Erik. Building Acoustics[M]. Taylor & Francis, New York, USA/NY, 2008.
[17]Simmons C. Structure-borne sound transmission through plate junctions and estimates of SEA coupling loss factors using the FE method[J]. Journal of Sound and Vibration ,1991,144 :215-227.
[18]周平,赵德有.加筋板的耦合损耗因子测量[J].振动与冲击,2006,25(8):165-168.
ZHOU Ping, ZHAO De-you. The experimental determination of coupling loss factor of stiffened plates[J]. Journal of Sound and Shock, 2006, 25(8):165-168.
[19]Bies D A, Hamid S. In situ determination of coupling loss factors by the Power Injection Method [J]. Journal of Sound and Vibration, 1980, 70:187-204.
[20]Langhe K DE, Sas P. Statistical analysis of the Power Injection Method[J]. Journal of the Acoustical Society of America, 1996, 100:291-303. R H, DeJong R G. Theory and application of statistical energy analysis [M]. London: Butterworth-Heinemann, 1995.
[2]姚德源,杨福家,王其政.统计能量分析原理及其应用[M]. 北京: 北京工业大学出版社,1995.
[3]Yap F F, Woodhouse J. Investigation of damping effects on statistical energy analysis of coupled structures [J]. Journal of Sound and Vibration 1996, 197:351-371.
[4]Tso Y K. An Investigation of the coupling loss factor for A cylinder/plate structure [J]. Journal of Sound and Vibration,1997, 199(4):629-643.
[5]Tso Y K. The transmission of vibration through a coupled periodic structure [J]. Journal of Sound and Vibration, 1998, 215(1):63-79.
[6]王宏伟,赵德有.平板与周期加筋阻尼板间耦合损耗因子的研究[J].船舶力学,2001,5(2) :55-61.
WANG Hong-wei,ZHAO De-you. Study on coupling loss factor between uniform plate and periodic stiffened damping plate [J]. Journal of Ship Mechanics,2001,5(2):55-61.
[7]Stell J A, Craik R J M. Statistical energy analysis of structure-borne sound transmission by finite-element methods [J]. Journal of Sound and Vibration, 1994, 178:553-561.
[8]Fredo C R. A SEA-like approach for the derivation of energy flow coefficients with a finite element model [J]. Journal of Sound and Vibration, 1997, 199:645-666.
[9]Yan H, Parrett A, Nack W. Statistical energy analysis by finite elements for middle frequency vibration [J].Journal of Sound and Vibration, 2000, 35: 297-304.
[10]Thite A N, Mace B R. Robust estimation of coupling loss factors from finite element analysis [J].Journal of Sound and Vibration,2007,303:814-831.
[11]卢兆刚,郝志勇,郑旭.基于有限元能量流模型的复杂耦合结构中低频段耦合损耗因子的计算[J].振动与冲击,2011,30(11): 42-46.
LU Zhao-gang, HAO Zhi-yong, ZHENG Xu. Coupling loss factor calculation of complex coupling structure based on finite element energy flow model[J].Journal of Sound and Shock,2011,30(11):42-46.
[12]王承权,张京立.舰船钢-铝结构过渡接头的应用及节点设计[J].船舶工程,2004,26(06):34-38.
WANG Cheng-quan, ZHAN Jing-li. Application and nodal point design of structural transition joint in Ship with steel-aluminum superstructure[J].Ship Engineering, 2004, 26(6):34-38.
[13]王承权,夏炳仁.铝合金上层建筑与钢主船体的新型焊接过渡接头[J].船舶工程,1999(4):26-28+34-3.
WANG Cheng-quan,XIA bing-ren. A new type of transition Joints for welding of aluminum alloy superstructure to steel hull structure [J].Ship Engineering,1999 (4): 26-28+34-3.
[14]许芝芳,于长亮.铝-钢过渡接头在船舶结构焊接中的应用[J].中国水运(下半月),2008(6):156-157.
XU Zhi-fang,YU Chang-liang. The application of aluminum- steel transition joints in Ship structure welding[J].China Water Transport,2008(6):156-157.
[15]John Banker, Job Visser. 铝-钢连接[J]. 造船师(中文版),2008( 9): 238-239.
John Banker, Job Visser. Aluminum-steel junction [J].Ship builder, 2008(9): 238-239.
[16]Vigran, Tor Erik. Building Acoustics[M]. Taylor & Francis, New York, USA/NY, 2008.
[17]Simmons C. Structure-borne sound transmission through plate junctions and estimates of SEA coupling loss factors using the FE method[J]. Journal of Sound and Vibration ,1991,144 :215-227.
[18]周平,赵德有.加筋板的耦合损耗因子测量[J].振动与冲击,2006,25(8):165-168.
ZHOU Ping, ZHAO De-you. The experimental determination of coupling loss factor of stiffened plates[J]. Journal of Sound and Shock, 2006, 25(8):165-168.
[19]Bies D A, Hamid S. In situ determination of coupling loss factors by the Power Injection Method [J]. Journal of Sound and Vibration, 1980, 70:187-204.
[20]Langhe K DE, Sas P. Statistical analysis of the Power Injection Method[J]. Journal of the Acoustical Society of America, 1996, 100:291-303.
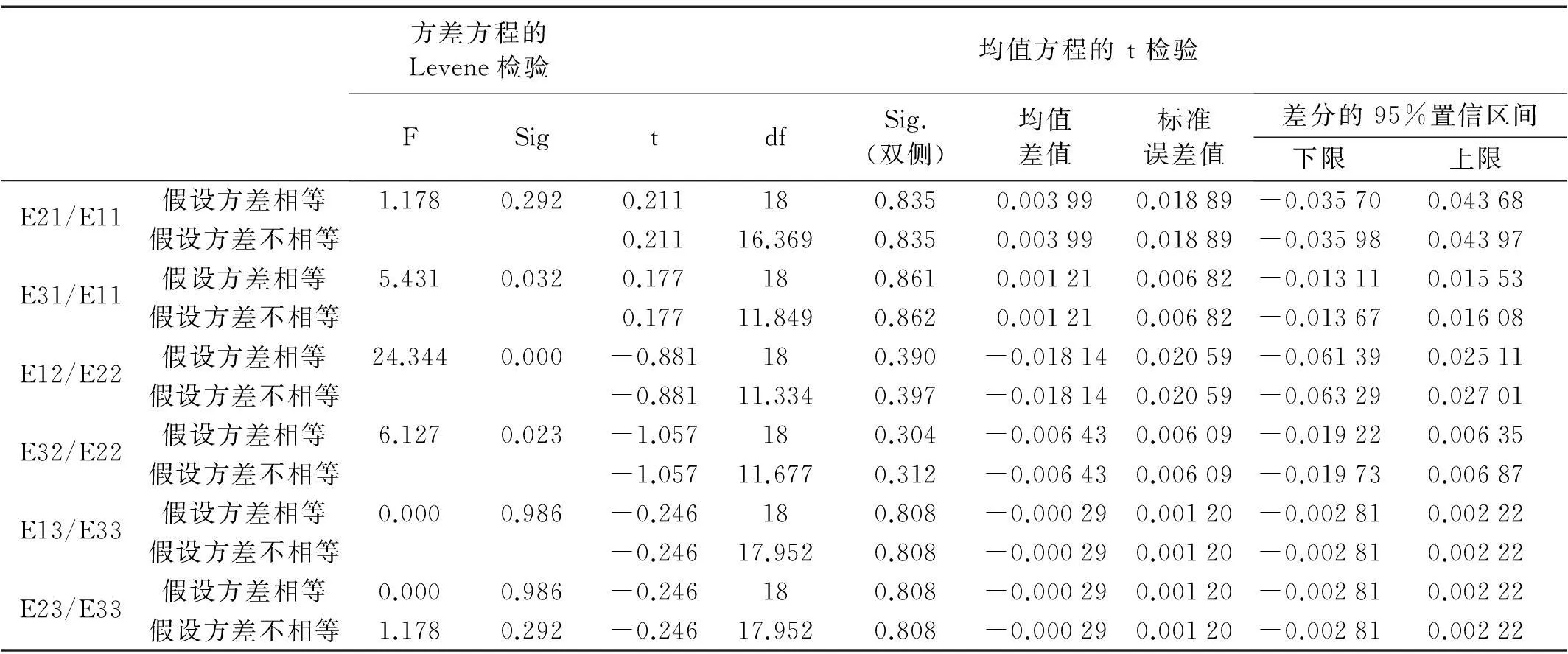
附表1 P3 和 P9独立样本检验结果
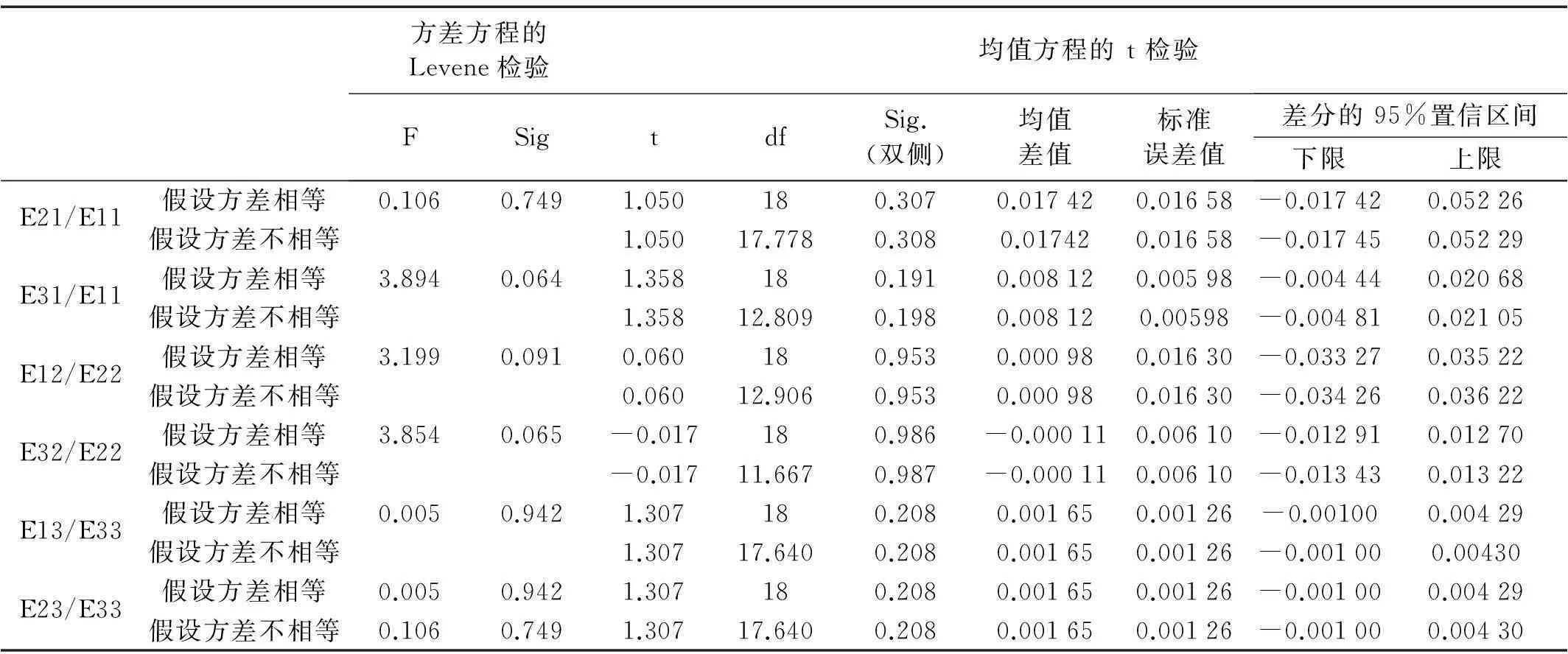
附表2 P6 和 P9独立样本检验结果

