具有形状记忆合金丝的复合材料轴转子系统的振动与稳定性
第一作者任勇生男,博士,教授,1956年7月生
具有形状记忆合金丝的复合材料轴转子系统的振动与稳定性
任勇生,赵仰生,安瑞君,代其义
(山东科技大学机械电子工程学院,青岛266590)
摘要:提出具有SMA丝的复合材料轴-盘-刚性支承转子系统的数学模型,研究转子系统的振动与稳定性。将轴视为一个平行于轴线方向埋入SMA丝的薄壁复合材料空心梁,盘为各向同性刚性圆盘, 轴位于刚性轴承上。基于变分渐进法(VAM)描述复合材料薄壁梁的变形,基于Brinson热力学本构方程计算SMA丝的回复应力,采用Hamilton原理推导出系统的运动方程,采用Galerkin法进行模型离散化和近似数值计算。着重分析SMA丝含量和初始应变对复合材料轴振动固有频率和转子系统临界转速的影响。研究结果表明,所建立的动力学模型能够用于揭示SMA对转子系统的振动与稳定性的影响机理。
关键词:形状记忆合金;复合材料轴;转子系统;振动与稳定性
基金项目:国家自然科学基金(11272190);山东省自然科学基金(ZR2011EEM031)
收稿日期:2013-08-26修改稿收到日期:2013-12-19
中图分类号:TH132文献标志码:A
基金项目:国家自然科学基金(51108376,50978218);国家科技支撑计划(2013BAJ08B03);高等学校博士学科点专项科研基金(20106120110003);陕西省科研项目(2012K12-03-01,2011KTCQ03-05)
Vibration and stability of a composite shaft-rotor system with SMA wires
RENYong-sheng,ZHAOYang-sheng,ANRui-jun,DAIQi-yi(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qindao 266510, China)
Abstract:A dynamical model of a rotor system containing a composite shaft with shape memory alloy (SMA) wires parallel to the shaft axis embedded, isotropic rigid disks and flexible bearings considered as linear springs and viscous dampers was presented and then used to predict the natural frequencies and dynamical stability of the rotor system. A composite thin-walled beam based on variational asymptotically approach(VAM) was employed to describe the deformation of the shaft. A thermo-mechanical constitutive equation of SMA proposed by Brinson et al. was used to calculate the recovery stress of the constrained SMA wires. Hamilton’s principle was used to derive the dynamic equations of the rotor system, they were discretized and solved with Galerkin’s method. The influcences of SMA wire content and initial strain on the natural frequencies and critical speeds of the rotor system were analyzed. Results showed that the proposed model can be used to reveal the effects of SMA on the dynamic characteristics of the rotor system.
Key words:shape memory alloy (SMA); composite shaft; rotor system; vibration and stability
纤维复合材料由于比强度和比刚度高、抗疲劳和减振性能好,在航空、汽车等高技术领域的转子系统中的柔性轴的结构设计中已经显示出良好的发展前景[1-2]。采用轻质纤维复合材料取代传统的金属材料不仅可以减轻结构的重量,同时还能够减少噪声、提高转子系统的抗振性能[3]。
将形状记忆合金(Shape Memory Alloy, SMA)埋入普通纤维复合材料产生的SMA混杂复合材料是一类应用广泛的智能材料系统,近几十年来,基于热激励诱发SMA马氏体相变从而改变结构刚度特性和弹性特性的结构调节原理的SMA混杂复合材料壳、板、梁的振动抑制研究,已经获得了一些重要的进展[4]。如果将SMA埋入复合材料轴,利用SMA丝控制轴的动力学特性,有望满足在高速运转状态下普通复合材料轴转子系统无法满足的动力学稳定性的要求,从而实现复合材料转子系统的安全高速运行。
Baz等[5]将复合材料驱动轴简化为实心轴,基于有限元方法研究了埋入SMA丝的复合材料驱动轴的静态特性和热特性。研究发现当SMA丝被激活时,可以提高轴的扭转刚度。Baz等[6]采用有限元分析和振动实验研究埋入SMA丝空心复合材料驱动轴动力学特性,结果表明激活NITI丝可以使轴的振动幅值减少了约50%。Tylikowskitffu等[7]将旋转轴简化为对称叠层圆柱壳,基于Liapunov 直接法分析了含有SMA丝的复合材料轴的动力稳定性,研究结果表明,激活SMA丝可以明显增加旋转轴的临界转速。Gupta等[8]基于瑞利法研究了空心复合材料轴内埋入SMA丝的双盘和单盘转子的固有频率和临界转速,分析了SMA丝的以及支承刚度变化的影响。研究发现,SMA的相变回复力能够抑制转子加速/减速通过临界转速时的共振响应。Sawhney等[9]进行了埋入SMA丝的纤维增强复合材料轴的制备和实验研究。Gupta等[10]设计了一个嵌入SMA丝的纤维增强复合材料轴的实验装置,实验结果表明,激活SMA丝的复合材料轴的固有振动频率显著增加。我们注意到,在上述所有这些研究中,有关杨氏模量、回复应力等描述SMA丝特性的重要力学参数主要出自一些有限的实验数据,此外,在复合材料轴动力学建模过程中仅仅考虑了轴的横向弯曲变形。
本文建立了一个具有SMA丝的复合材料轴-盘-轴承转子系统的数学模型,研究了该转子系统的振动与稳定性。将轴视为一个埋入SMA丝薄壁复合材料空心梁,SMA丝与轴线平行布置,固结于轴上的盘为各向同性刚性圆盘,轴位于刚性轴承上。采用Brinson热力学本构方程[11]计算SMA丝的回复应力,由VAM[12]描述拉-弯-扭耦合复合材料薄壁梁的变形,并且计入横向剪切变形的影响。基于Hamilton原理建立转子系统的运动方程,采用Galerkin方法对运动方程进行离散化,通过数值计算得到轴的固有频率以及系统的固有频率随转速变化的Campbell图,着重分析了固有频率和临界转速随SMA丝含量和初始应变的变化规律,揭示了SMA对转子系统动力学特性的影响机理。
1振动方程
图1表示长度为L、厚度为h的绕其轴线以定常角速度旋转的封闭截面纤维复合材料薄壁轴。惯性坐标系为(x,y,z),局部坐标系为(x,s,ξ),其中环向坐标s沿着薄壁梁中面切线逆时针方向,ξ沿着薄壁梁中面法线方向。SMA丝平行于复合材料轴的轴线埋入基体内。

图1 具有SMA丝的旋转复合材料轴 Fig.1 Rotating composite shaft with SMA wires
从文献[12]的位移场表达式出发,进一步引入横向剪切变形的影响,于是薄壁轴横截面上的任意一点沿着x,y,z方向的位移假设如下
u1(x,y,z,t)=U1(x,t)-y(s)θy(x,t)-
z(s)θz(x,t)+g(s,x,t)
u2(x,y,z,t)=U2(x,t)-zφ(x,t)
u3(x,y,z,t)=U3(x,t)+yφ(x,t)
(1)
其中:U1(x,t),U2(x,t),U3(x,t)分别表示横截面沿着x,y,z方向的刚体位移;φ(x,t),θy(x,t),θz(x,t)分别表示横截面绕x轴的扭转角以及绕y,z轴的扭转角。y,z表示横截面中心围线上的点的坐标,是环向坐标s的函数。
假定薄壁梁的翘曲函数g(s,x,t)具有如下形式
(2)
上述等式右端的四项依次是与扭转、轴向拉伸、绕z轴弯曲和y轴弯曲有关的翘曲分量,其中G(s)的物理意义为扭转率,g1(s)的物理意义为轴向应变,g2(s)和g3(s)的物理意义为沿y,z方向的弯曲曲率。
在方程(1)和(2)中,θy(x,t),θz(x,t)可以表示如下
(3)
根据文献[12]几何方程,由位移方程(1)可以导出横截面正应变和面内剪应变γxx和γxs的表达式,并且依照文献[13],对横向剪应变γxξ的表达式也做出假设。因此,考虑剪切变形的薄壁轴的几何方程可以写出如下
(4)
为了导出复合材料轴的振动方程,利用Hamilton原理
(5)
其中:U和T分别为应变能和动能,分别由下式确定
(6)

从方程(5),可以推导出具有周向均匀刚度配置(CUS)构型的复合材料轴的振动偏微分方程组如下
(7)
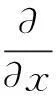
混杂SMA丝的复合材料的弹性系数按照下列混合率进行计算
E1=E1m(1-Vs)+EsVs
ν12=ν12m(1-Vs)+νsVs
(8)
其中,下标m,s分别表示复合材料基体与SMA丝。E,G,υ分别表示杨氏模量,剪切模量和泊松比,Vs和Vm分别为SMA丝与基体材料的体积比含量。Asma,ATotal分别表示所有埋入SMA丝的横截面之和以及复合材料轴的横截面,且
(9)
其中:d为SMA丝的直径,n为埋入SMA丝的个数。
引入SMA丝对复合材料轴的作用,则可推出如下运动方程
(10)
其中:NSMA和NΔT表示SMA丝产生的沿轴线方向的受限回复应力的合力以及轴向温度载荷
(11)
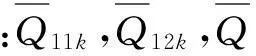
升温过程:
(12)
降温过程:
(13)
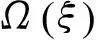
在SMA丝复合材料轴的模型基础上,进一步考虑盘和轴承的影响。假设圆盘为刚性的,由各向同性材料制成,而轴承简化为线性弹簧和粘滞阻尼器。
引入圆盘和轴承的SMA丝复合材料轴的运动方程导出如下
(14)
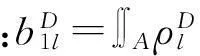
2方程求解
假定弯曲位移U2(x,t),U3(x,t)和转角θy(x,t),θz(x,t)具有下列形式
(15)
式中:Uj,Θj都是待定的位移参数,αj(x),ψj(x)则表示复合材料轴的形函数。
将(15)代入方程组 (14),采用Galerkin法,得出转子系统的振动方程组
(16)
其中,M,C,KΩ,K1的表达式如下
(17)
(18)
(19)
(20)

3数值结果与讨论
表1表示不考虑剪切的悬臂复合材料轴的旋转/非旋转固有频率的本文计算结果和文献[14]的结果的对比,其中计算参数和无量纲化方法同文献[14]。由表1可以看出,二者的结果符合得很好。
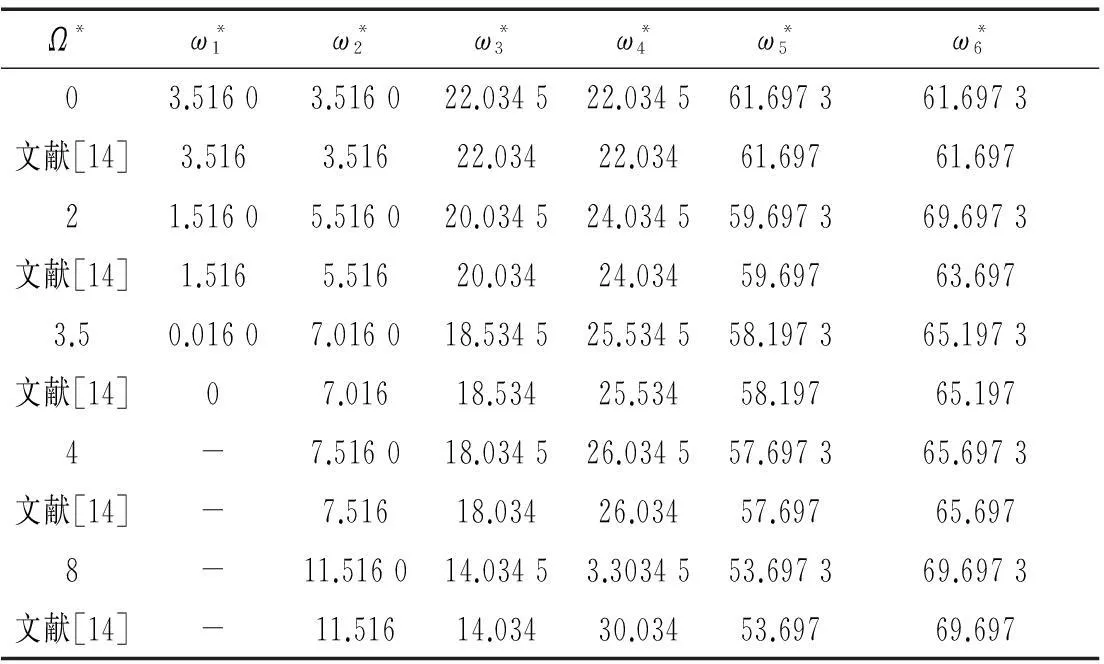
表1 不计剪切的悬臂复合材料轴的固有频率结果对比


表2 复合材料性能参数 [15]

表3 SMA的材料参数 [16]
为了便于分析,引入标准化因子ω0=138.85 rad/s,其意义为旋转复合材料轴在铺层角为0°,转速为0,并且NSMA=0和NΔT=0时的固有频率。无量纲的固有频率和转速分别为ω*=ω/ω0,Ω*=Ω/ω0。
图2表示含SMA丝(红线)和不含SMA丝(黑线),复合材料轴的固有频率随转速的变化曲线。结果表明,在转速为0,即不计陀螺效应时,复合材料轴的固有频率为一个点。随着转速的增加,即计入陀螺效应时,复合材料轴的固有频率曲线分叉成上、下两个分支,分别记为Upper(上固有频率)和Lower(下固有频率),它们分别对应于正进动涡动和反进动涡动。当下分支随着转速的增加而减小至0时,所对应的转速称为临界转速Ωcr。对应于每一阶频率,都有一个与之相对应的临界转速。对比上述两种结果,可以发现,诱发SMA丝相变可以提高轴静止状态的固有频率,提高旋转复合材料轴发生动力不稳定的临界转速。
图3中表示对应于不同SMA丝含量的第一阶固有频率随转速的变化曲线。可以看到旋转轴的临界转速随着SMA丝含量的增加而增加,这是因为当SMA丝的含量增加时,轴向张力随之增加,于是,轴的刚度也随之增加,从而导致固有频率的增加。
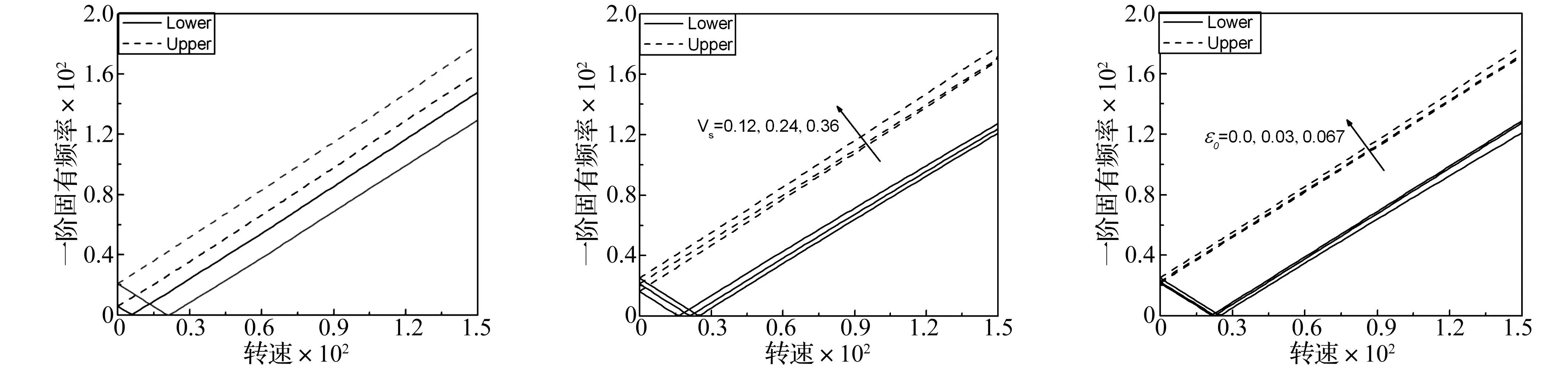

图2 含SMA和不含SMA的传动轴第一阶固有频率随转速的变化曲线(θ=30°,T=50℃,Vs=0.24)Fig.2Thefirstnaturalfrequencyvs.rotatingspeedofshaftwithSMAandwithoutSMA(θ=30°,T=50℃,Vs=0.24)图3 不同SMA丝含量情况下的一阶固有频率随转速变化曲线(θ=30°,T=50℃,ε0=0.067)Fig.3Thefirstnaturalfrequencyvs.rotatingspeedfordifferentSMAfibercontents(θ=30°,T=50℃,ε0=0.067)图4 不同SMA丝初始应变的一阶固有频率随温度变化曲线(Vs=0.36,T=50℃,θ=30°)Fig.4Thefirstnaturalfrequencyvs.rotatingspeedfordifferentSMAfiberinitialstrain(Vs=0.36,T=50℃,θ=30°)
图4表示不同SMA丝的初始应变下的第一阶固有频率随转速的变化曲线,从图中可以看出,轴的固有频率随着初始应变的增加而增加。

图5 不同SMA丝含量情况下的一阶固有频率随温度 变化曲线(Ω * =5 rad/s,θ=30°, ε 0=0.067) Fig.5 The first natural frequency vs. temperature for different SMA fiber contents (Ω* =5 rad/s,θ=30°, ε 0=0.067)
图5表示激励温度对第一阶固有频率的影响曲线,其中给出对应于三种不同SMA丝含量的结果。温度变化从0℃上升到100℃(M→A),然后在从100℃下降到0℃(A→M)。从图中可以看出,固有频率随温度的变化曲线是典型的迟滞迴线。在一个热循环周期内,固有频率随温度的变化可以分为两个阶段:增加阶段和减少阶段;在马氏体向奥氏体相变的过程中,固有频率随着温度的增加而增加,而从奥氏体向马氏体相变的过程,固有频率随着温度的减小而下降;由于转速不为零,因此派生出两组迟滞迴线,在图中分别用“Upper”和“Lower”加以区分。容易发现,随着SMA丝含量的增加,固有频率也随之提高,迟滞迴线向上发生整体迁移。
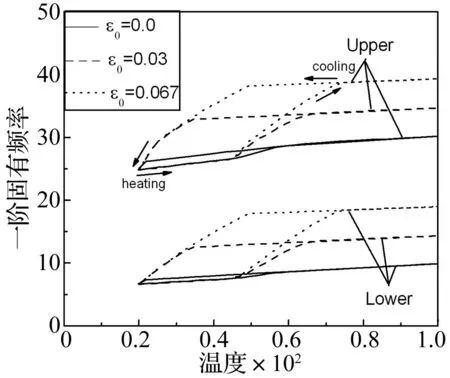
图6 不同SMA丝初始应变的一阶固有频率随 温度变化曲线(Vs=0.24, θ=30°, Ω * =10 rad/s) Fig.6 The first natural frequency vs. temperature for different SMA fiber initial strain(Vs=0.24,θ=30°,Ω * =10 rad/s)
图6表示对应于SMA丝的不同初始应变的第一阶固有频率随温度的变化曲线。从图中可以看出,与SMA丝含量的影响不同,在升、降温阶段的某些温度区间,不同初始应变下的迟滞迴线会相互重叠在一起,迟滞迴线的形状似乎会发生较为明显的改变。
下面进一步研究如图7所示的SMA丝复合材料传动轴-盘-轴承系统的临界转速。单个刚盘位于轴的中央位置,轴的两端用轴承支承。轴的铺层方式采用[θ]10,轴承和刚盘的尺寸和性能参数如表4所示。
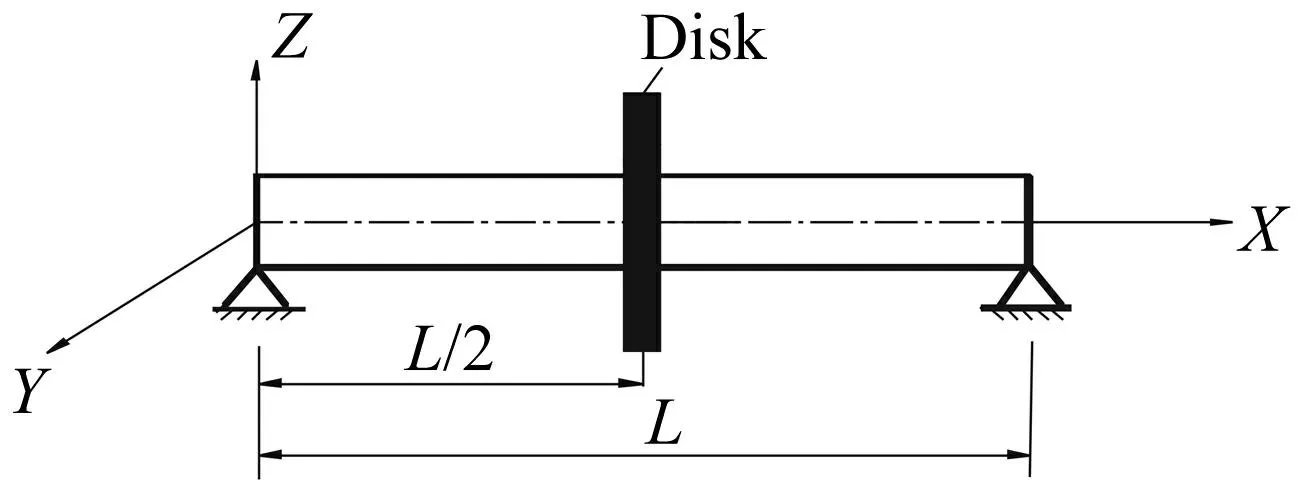
图7 单刚盘转子系统 Fig.7 A rigid disk rotor

质量与惯性矩数值bD1l/kgbD4l/(kg·m-2)bD5l/(kg·m-2)2.43640.19010.1901
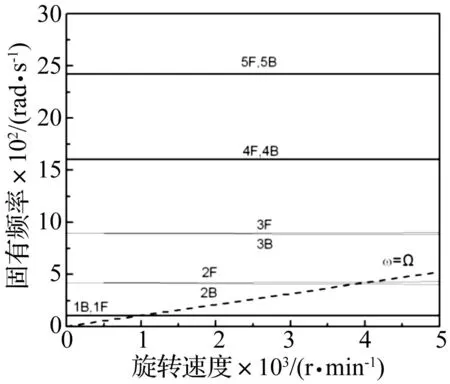
图8 不含SMA的轴-盘-刚性轴承系统的Campbell图 Fig.8 The Campbell diagram of the shaft-disk-stiff bearings system without SMA wires

图9 含SMA丝的轴-盘-刚性轴承系统的Campbell图 Fig.9 The Campbell diagram of the shaft-disk-stiff bearings system with SMA wires
图8和图9分别表示不含SMA丝和含SMA丝的转子系统的Campbell图。其中展示了前5阶涡动频率,“F”表示正进动,“B”表示反进动。图中涡动频率曲线与直线ω=Ω的交点为转子系统的临界转速,用Ωcr表示。从图中可以看出第二阶和第三阶涡动频率曲线有相对较为明显分叉,这可能是由于轴的振动和刚盘的振动相耦合造成的。通过比较图8和图9可以明显看到,加入SMA丝能够明显地提高转子系统的临界转速。
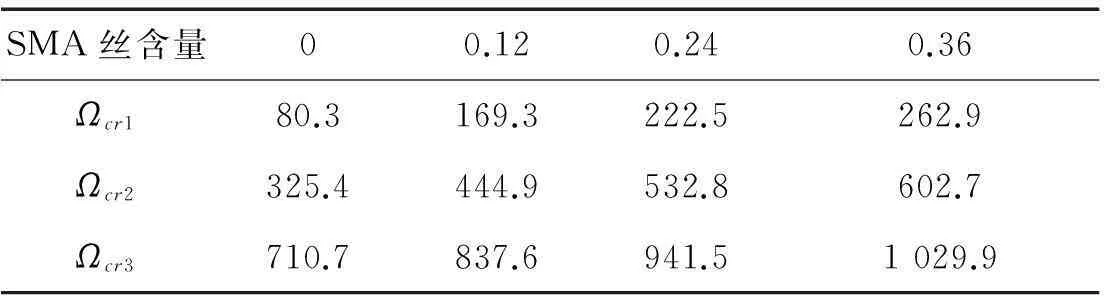
表5 不同SMA丝含量对应的临界转速
表5和表6分别表示具有不同SMA丝含量和不同SMA初始应变的转子系统的前3阶临界转速。从表5中可以清楚地看出,随着SMA丝含量的增加,转子系统的临界转速随之增加;同样,由表6可看出SMA丝的初始应变对转子临界速度也有着类似的影响。因此,通过适当地调节SMA丝的含量和初始应变,能有效地增强转子系统的稳定性。
为了验证采用Galerkin法计算复合材料轴固有频率结果的收敛性,取不同项数的振型函数进行了计算,结果如图10所示。其中10(a)和(b)分别对应Lower和Upper。由图可见,当振型函数项数取N=5时,固有频率-温度变化曲线已经与N=4,3对应的曲线完全重合,说明本文采用的近似数值计算方法具有很好的收敛性。
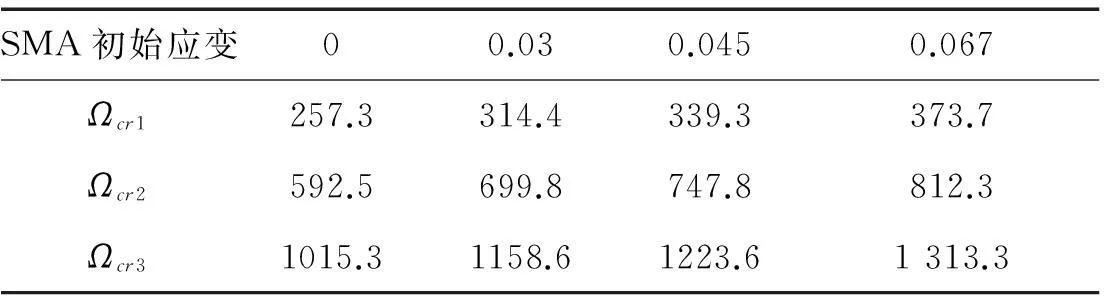
表6 不同SMA初始应变对应的临界转速
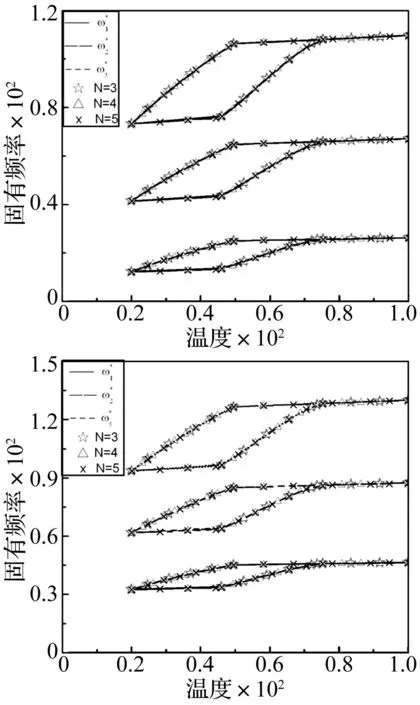
图10 固有频率关于振型项数的收敛性 (Ω* =5 rad/s, θ=30°, ε 0=0.067) Fig.10 Convergence of the first natural frequencies with respect to number of mode shapes (Ω* =5 rad/s, θ=30°, ε 0=0.067)
4结论
研究了一个由埋入SMA丝的复合材料轴、盘和轴承构成的转子系统的振动与稳定性。SMA丝平行于复合材料轴的轴线方向铺设。基于VAM复合材料薄壁梁理论、Brinson热力学本构方程和Hamilton原理建立系统的运动方程,采用Galerkin法进行模型离散化和近似求解。分析结果表明:
(1)在复合材料轴内埋入SMA丝可以显著提高轴的静态和旋转固有频率;
(2)温度的变化对轴的动力学特性有重要的影响,在一个热循环周期内,由于马氏体向奥氏体相变(M→A)以及逆相变(A→M)的发生,固有频率随温度的变化曲线表现为典型的迟滞迴线;
(3)随着SMA丝含量的增加,转子系统的临界转速随之增加;另一方面,提高SMA丝的初始应变也能增加转子系统的临界速度,从而增强转子系统的动力稳定性。
参考文献
[1]王震鸣,杜善义,张衡,等.复合材料及其结构的力学、设计、应用和评价(第二册)[M].哈尔滨:哈尔滨工业大学出版社,1998.
[2]Hetherington E L, Kraus R E, Darlow M S. Demonstration of a super critical composite helicopter power transmission shaft[J].Journal of American Helicopter Society,1990,35(1):23-28.
[3]Faust H, Mack J, Spencer B. A composite rotor shaft for the Chinook[J]. Journal of the American Helicopter Society,1984 29: 54-58.
[4]任勇生,王世文,李俊宝,等.形状记忆合金在结构主被动振动控制中的应用[J].力学进展,1999,29(1):19-33.
[5]Baz A,Chen T.Torsional stiffness of Nitinol-reinforced composite drive shafts[J]. Composites Engineering, 1993, 3(12): 1119-1130.
[6]Baz A, Chen T. Performance of nitinol reinforced drive shafts[C]. In Smart Structure and Intelligent Systems, SPIE 1917, 1993, 791-808.
[7]Tylikowski A, Hetnarski R B. Semiactive control of a shape memory alloy hybrid composite rotating shaft[J].International Journal of Solids and Structures,2001,38:9347-9357.
[8]Gupta K. Critical speed analysis of fibre-reinforced composite rotor embedded with shape memory alloy wires[J]. Int. J. Rotat. Mach., 2000, 6(3):201-213.
[9]Sawhney S, Jain S K. Vibration control of fibre-reinforced composite rotor using shape memory alloy (SMA) wires[D]. IT Delhi, 2001, New Delhi. BTech Dissertation.
[10]Gupta K, Sawhney S, Jain S K,et al. Stiffness characteristics of fibre-reinforced composite shaft embedded with shape memory alloy wires[J]. Defence Science Journal, 2003, 53(2): 167-173.
[11]Brinson L C. One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material fuctions and redefined martensite internal variable [J]. J. Intelligent Mat. Syst. Struct. 1993, 4: 229-242.
[12]Berdichevsky V, Armanios E, Badir A. Theory of anistropic thin-walled closed-cross-section beams[J]. Composites Engineering, 1992,2:411-432.
[13]Song O, Librescu L. Structural modeling and free vibration analysis of rotating composite thin-walled beams[J].Journal of the American Helicopter Society,1997:358-369.
[14]Banerjee J R, Su H. Development of a dynamic stiffness matrix for free vibration analysis of spinning beams[J]. Comput Struct, 2004,82: 2189-2197.
[15]Song O, Jeong N H, Librescu L. Implication of conservative and gyroscopic forces on vibration and stability of an elastically tailored rotating shaft modeled as a composite thin-walled beam[J] J. Acoust. Soc. Am.,2001,109(31):972-981.
[16]Sun S S, Sun G, Han F, et al. Thermoviscoelastic analysis for a polymeric composite plate with embedded shape memory alloy wires[J]. Composite Structures, 2002, 58: 295-302.
[17]Chang M Y, Chen J K, Chang C Y. A simple spinning laminated composite shaft model[J]. Int. Journal of Solids and Structures, 2004,41:637-662.
附录
复合材料轴横截面的刚度系数:
(A.1)

