黄金分割控制在无人机姿态控制中的应用
王彦龙,杨 喆,陈 阳
(1.中国科学院 长春光学精密机械与物理研究所,长春 130033; 2.北京理工大学,北京 100010)
黄金分割控制在无人机姿态控制中的应用
王彦龙1,杨喆2,陈阳1
(1.中国科学院 长春光学精密机械与物理研究所,长春130033; 2.北京理工大学,北京100010)
摘要:针对无人机气动耦合较强、难以建立精确模型的特点,以舵偏角为输入量,以姿态角为输出量,建立了无人机姿态控制系统的特征模型;分别采用线性和非线性黄金分割控制方法设计了无人机姿态控制律并进行了仿真试验;仿真结果表明:采用线性和非线性黄金分割设计的姿态控制系统稳定,无稳态误差,能够满足无人机姿态控制精度要求;非线性黄金分割控制器的过渡性能优于线性黄金分割控制器,并且具有较好的抗干扰能力。
关键词:无人机;特征模型;黄金分割;姿态控制
无人机具有使用机动灵活、对人员场地要求不高等特点,近年来已被广泛应用于军事、民用和科研领域。无人机为了安全高效的完成飞行任务,需要具有良好的飞行控制系统。姿态控制是飞行控制中的重要方面,直接影响无人机的飞行性能[1]。在进行无人机姿态控制器设计时,经常面临以下问题:无人机在实际工作过程中,受到多种因素的影响,如运动耦合、惯性耦合、气动耦合和控制耦合以及协调控制问题等,其自身和环境情况难以精确描述,机体特性和环境在运行过程中会发生不可预测的变动,难以建立精确地运动学模型,这给控制器的设计带来了困难;此外,如果建立的模型阶次较高,也不利于低阶控制器的设计。文献[2]中提出了特征建模的思想,简化了难以建立精确动力学模型的复杂对象的建模过程;文献[3]中通过建立特征模型的方法对无人机的姿态回路进行分析,设计出了一种基于系统特征模型的智能控制方法;文献[4-6]中分别采用非线性方法设计了控制器,完成了对无人机的高效控制;文献[7]中在传统经典PID控制算法的基础上应用了一种带死区变增益PID自适应控制方法,有效的抑制了大扰动条件下对无人机姿态、位置的影响;文献[8]中针对无人机俯仰姿态的控制律设计了一种模糊PID飞行控制器,并对这种PID控制器的控制特点及参数设计规则等进行描述。本文针对姿态控制系统设计过程中存在的建模问题,采用特征建模的方法解决利用低阶控制器实现对于高阶复杂对象的控制性能要求的问题;采用黄金分割控制方法设计姿态控制器,保证参数未知定常系统在过渡过程阶段,参数估计未收敛情况下闭环系统稳定。
1无人机运动学模型
在完成无人机控制系统的设计之前,首先分析和建立无人机的运动学方程组[9]。无人机绕质心的旋转运动,可以表示成式(1)的形式
(1)
其中,Mx为滚转力矩,My为偏航力矩,Mz为俯仰力矩,q为动压,S为无人机的特征面积,L为特征长度,mx、my、mz分别称为滚转力矩系数、偏航力矩系数和俯仰力矩系数。根据在实验过程中实际采用的方法,将式(1)修改成式(2)的形式
(2)
由式(2)可以看出,力矩系数和攻角、侧滑角以及舵偏角有关。将实验数据代入,采用最小二乘法求出它们之间的关系表达式,也就建立了力矩和攻角、侧滑角以及舵偏角之间的关系。
经过计算,有以下关系式成立
(3)
式(3)就是俯仰力矩、偏航力矩和滚转力矩的表达式,其中,bA为机翼的平均气动弦长。在机体坐标系上建立无人机绕质心转动的动力学方程,有式(4)的形式
(4)
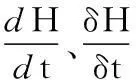
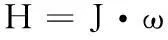
(5)
式(5)中,J为惯性张量,矩阵表示形式如式(6)
(6)
为了确定无人机在空间的姿态,建立描述无人机机体相对地面坐标系姿态变化的运动学方程,即建立姿态角ϑ、φ、γ变化率与无人机相对地面坐标系转动角速度分量ωx、ωy、ωz之间的关系。根据地面坐标系与机体坐标系之间的转换关系可得无人机绕质心转动的运动学方程如式(7)
(7)
2特征模型的建立
2.1 特征建模的基本原理
所谓特征建模,就是根据对象动力学特征、环境特征和控制性能要求相集合进行建模,而不仅以对象精确的动力学分析来建模。特征建模与对象动力学建模不同,特征建模主要抓住控制量与要求输出变量之间的特征关系,由特征变量和特征参量组成特征模型。特征模型与高阶系统的降阶模型不同,它是把高阶系统有关信息都压缩到几个特征参量之中,并不丢失信息,一般情况下特征模型用慢时变差分方程描述。
当被控对象满足一定条件,在适当选取采样周期Δt的条件下,当要实现位置保持或者位置跟踪控制时,其特征模型可用一个二阶时变差分方程形式描述。即
(8)
由于工程上对最小相位系统g1(k)可忽略,则式(8)可以简化为
(9)
2.2 无人机姿态控制特征模型的推导
由前面的内容可知,无人机绕质心转动的动力学标量方程为式(6)的形式。根据地面坐标系与弹体坐标系的转换关系可得
(10)
那么就有如下关系成立
(11)
由式(3)、(6)和(11)可整理成下面的形式:
(12)
取状态变量为
(13)
取输入控制量分别为
(14)
将式(12)改写为差分形式,整理得:
(15)
其中
(16)
通过以上推导得到的即为无人机的姿态控制系统特征模型。
3黄金分割控制律设计和仿真
3.1 黄金分割控制的基本概念
黄金分割,又叫“中外”比,比值为0.618。黄金分割控制方法的基本含义,就是在控制器设计过程中引入黄金分割比。
黄金分割控制方法由吴宏鑫院士首先提出,接受了大量实际控制工程的考验。与其他自适应控制和模糊控制等智能控制方法相比,黄金分割控制方法具有其独特的优点:黄金分割控制应用于参数未知定常系统,可以保证在过渡过程阶段参数未收敛情况下闭环系统稳定,当控制系统的控制性能要求不高时,黄金分割控制器的参数不需要研究人员在现场试凑。
3.2 线性黄金分割姿态控制律
3.2.1线性黄金分割控制律设计
无人机姿态控制系统结构如图1所示。其中,xd(k)为给定的姿态角,x(k)为输出的姿态角,u(k)为控制系统的控制变量。
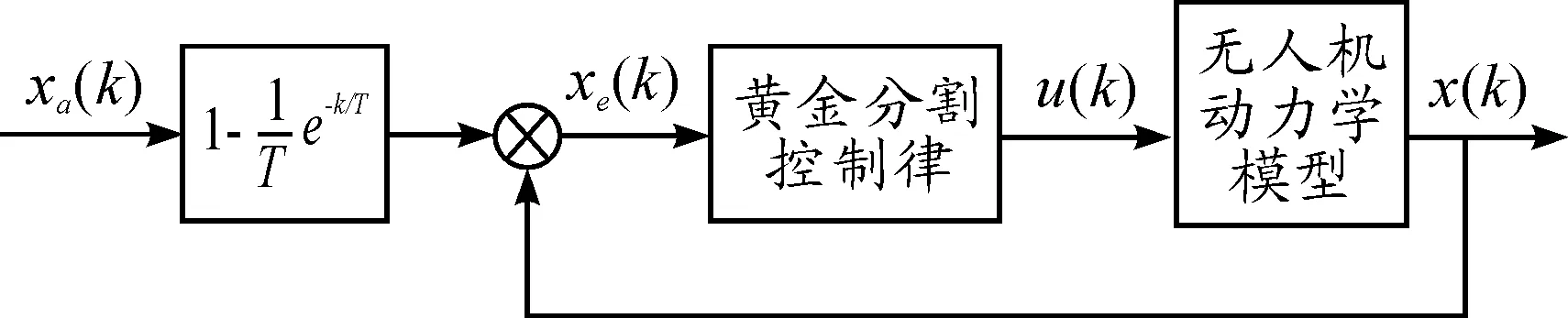
图1 无人机姿态控制系统结构
本文中姿态控制系统的基本原理:控制律根据控制偏差计算出舵偏角控制量,通过舵偏角的改变,完成力矩系数和力矩的改变,最终实现弹体姿态的改变。
设稳定的线性定常二阶对象的差分方程为
(17)
对象系数α1、α2、β0未知,将黄金分割应用于实际的控制器设计,控制器为
(18)
可以得到机体姿态的线性黄金分割控制律:
(19)
其中
3.2.2线性黄金分割控制律仿真试验
作为实际的控制系统,各个控制量不能无限大,仿真时需要对控制量的输入和被控量的改变进行幅值限制。参照实验获得的数据,设定仿真初始条件如下:
1) 无人机的转动惯量
(21)
2) 特征面积:S=0.15m2
3) 大气密度选用平均海平面大气特征值:
ρ0=1.22 5 kg·m-3
4) 舵偏角幅值:≯16°
5) 舵偏角速度:≯150°·s-1
仿真步长取Δt=0.02s;攻角和侧滑角为外回路输入量,都设为2°。
以滚转通道为例进行仿真,通过仿真结果验证所设计的姿态控制律:取无人机初始时刻姿态角和角速度均为0,给定姿态角[ϑ,ψ,γ]=[0,0,10°],仿真结果如下:
从图2中可以看出,无人机滚转通道姿态控制系统闭环稳定,经过0.9s后进入稳态,无稳态误差;初始阶段俯仰角存在较大耦合,但是很快得到抑制;偏航角耦合幅值较小,存在进入稳态时间较长的问题;图3中的舵偏角和舵偏角速度在初始阶段存在震荡,在0.5s后都稳定了下来。
通过分析仿真结果可以看出,采用线性黄金分割控制律设计的无人机姿态控制系统闭环稳定,无稳态误差,控制系统设计简单。
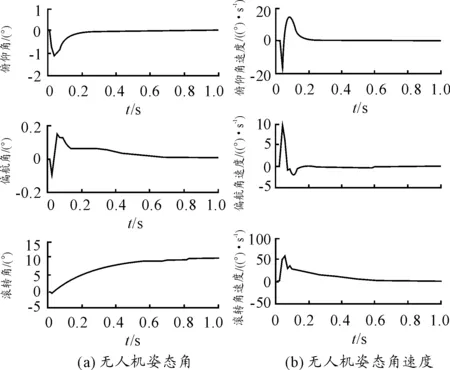
图2 线性黄金分割控制律下无人机姿态角、

图3 线性黄金分割控制律下无人机舵偏角、
3.3 非线性黄金分割控制律
3.3.1非线性黄金分割控制律设计
从前面的仿真结果可以看出,线性黄金分割控制器和简化特征模型组成的闭环系统是稳定的,但是系统过渡过程较长,因此,在线性黄金分割控制律的基础上,构造一种非线性黄金分割控制律:
(22)
其中,η1、η2和μ均为常数。
应用该非线性控制律设计本文的控制器:
(23)
3.3.2非线性黄金分割控制律仿真试验
以滚转通道为例,仿真条件与前面的相同:取无人机初始时刻姿态角和角速度均为0,给定姿态角[ϑ,ψ,γ]=[0,0,10°]。仿真结果如下(图4、图5、图6):
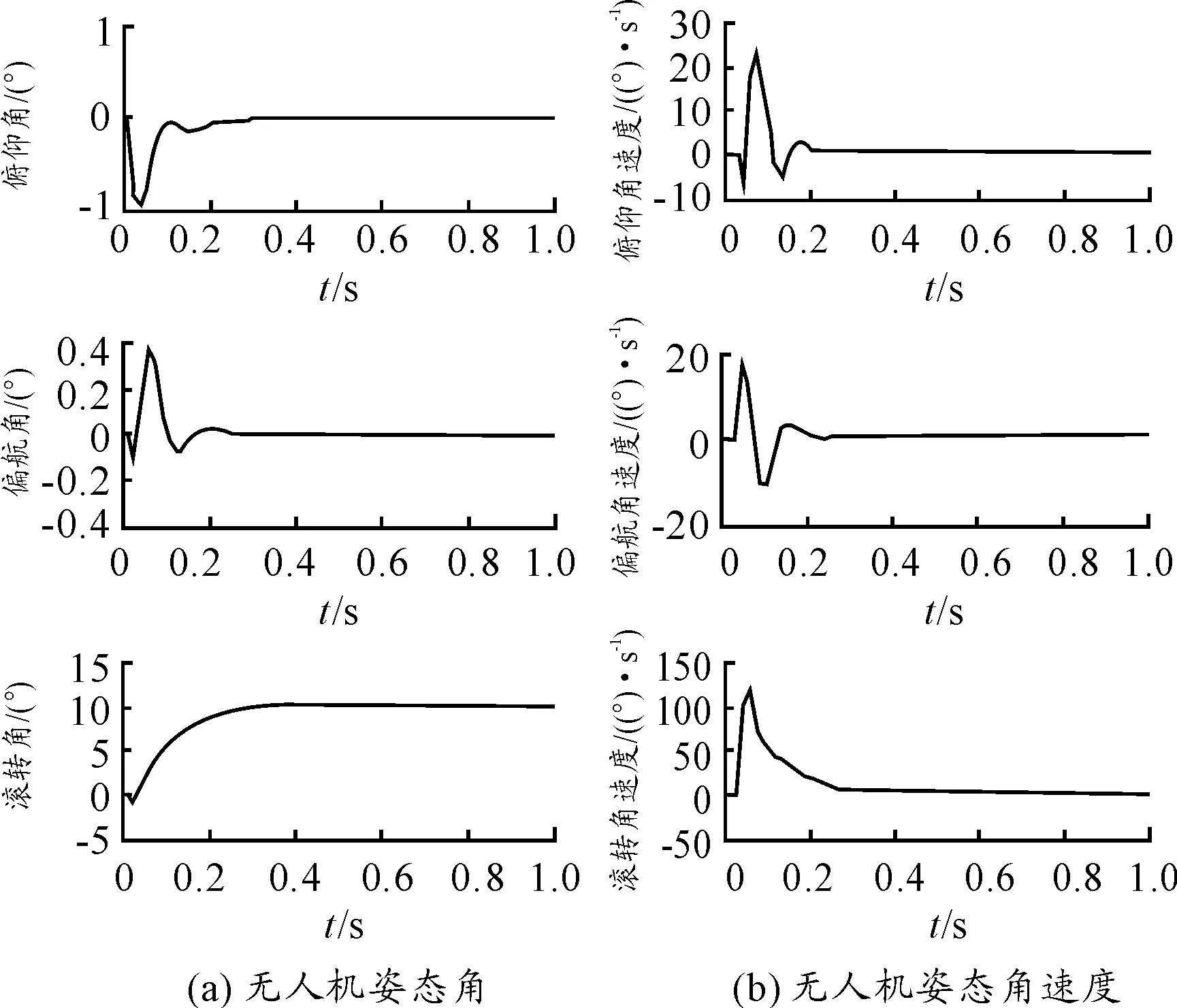
图4 非线性黄金分割控制律下无人机姿态角、

图5 非线性黄金分割控制律下舵偏角、
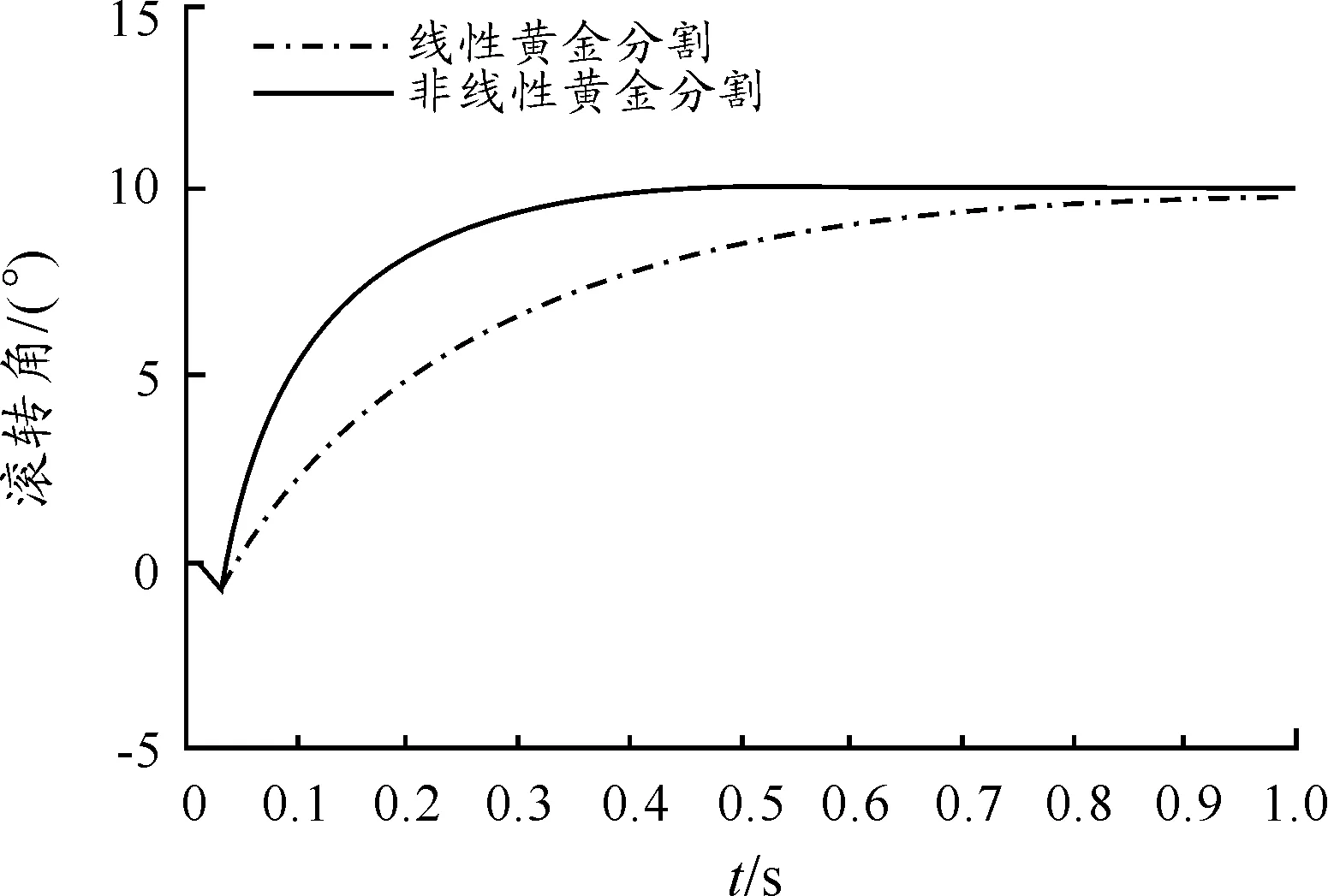
图6 线性和非线性控制效果对比图
从仿真结果可以看出,采用非线性黄金分割控制律设计的无人机姿态控制系统经过0.35s达到稳态,与之前的 0.9s的结果相比有较大提高;系统没有超调和稳态误差,过度过程平滑、迅速;在进行滚转角机动时,非线性黄金分割控制律对于动力学耦合带来的俯仰角和偏航角的影响有明显的抑制作用。
在保持其他仿真条件不变的情况下,在无人机的三个轴向上分别引入形如式(23)的干扰力矩:
(24)
仿真结果如下(图7、图8):

图7 干扰力矩作用下无人机姿态角、

图8 干扰力矩作用下舵偏角、舵偏角速度
从仿真结果可以看出,采用非线性黄金分割控制律设计的无人机姿态控制系统具有较强的抗干扰能力,在扰动量作用下,系统仍然能够保持良好的动态性能,无稳态误差。
4结论
本文对黄金分割控制方法在无人机姿态控制中的应用展开了研究。该方法结合试验数据,综合考虑控制系统的输入和输出,在保留通道间耦合量的情况下,建立了以舵偏角为控制输入、姿态角为状态输出的无人机控制特征模型;在此基础上,分别应用线性和非线性黄金分割控制方法,设计了无人机的姿态控制器;通过计算机仿真实验,对无人机姿态控制特征模型和控制器的正确性进行验证。结果表明:采用非线性黄金分割控制方法设计的无人机姿态控制器优于采用线性黄金分割得到的结果,所设计的控制器闭环系统稳定,过渡性能良好,无稳态误差,能够克服通道间的耦合作用,达到良好的控制效果。黄金分割控制方法在解决无人机姿态控制等随动问题中有着良好的应用前景。
参考文献:
[1]SchrageDP,VachtsevanosG.Software-enabledcontrolforintelligentUAVs[C]//Proceedingsofthe1999IEEEInternationalSymposiumonComputerAidedControlSystemDesign.Koha-la,CoastHI,USA,1999:22-27.
[2]吴宏鑫,胡军,解永春.基于特征模型的智能自适应控制[M].北京:中国科学技术出版社,2009.
[3]梅劲松,屈蔷,袁家斌.基于特征模型的某型无人机智能PID控制器[J].南京航空航天大学学报,2006,38(4):483-486.
[4]YangCD,KungCC.NonlinearH∞flight control of general six-degree-of-freedom motions[J].Journal of Guidance,Control and Dynamics,2000,23(2):278-288.
[5]WangQ,StengelRF.Robustnonlinearflightcontrolofahigh-performanceaircraft[J].IEEETransactionsonControlSystemsTechnology,2005,13(1):15-26.
[6]ChenM,GeSS,RenB.Robustattitudecontrolofhelicopterswithactuatordynamicsusingneuralnetworks[J].IETControlTheoryandApplications,2010,12(4):2837-2854.
[7]陶冶,房建成,盛蔚.一种微小型无人机带死区变增益PID自适应控制器的设计与实现[J].自动化学报,2008,34(6):716-721.
[8]张晨,李小民.无人机飞行控制PID参数的模糊自整定技术研究[J].四川兵工学报,2009,30(7):85-88.
[9]吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005.
(责任编辑杨继森)
收稿日期:2015-01-20
基金项目:国家自然科学基金青年基金(51305421);吉林省科技发展项目青年基金(20140520137JH)
作者简介:王彦龙(1988—),男,研究实习员,硕士,主要从事飞行器导航制导与控制研究。
doi:10.11809/scbgxb2015.07.032
中图分类号:V249.122+.2
文献标识码:A
文章编号:1006-0707(2015)07-0125-05
本文引用格式:王彦龙,杨喆,陈阳.黄金分割控制在无人机姿态控制中的应用[J].四川兵工学报,2015(7):125-129.
Citationformat:WANGYan-long,YANGZhe,CHENYang.ApplicationofGoldenSectioninUAVAttitudeControlSystem[J].JournalofSichuanOrdnance,2015(7):125-129.
ApplicationofGoldenSectioninUAVAttitudeControlSystem
WANGYan-long1, YANG Zhe2, CHEN Yang1
(1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,
Changchun130033,China; 2.BeijingInstituteofTechnology,Beijing100010,China)
Abstract:A characteristic model was built to solve the problems including creating an accurate control model and solving strong aerodynamic coupling issue. The rudder deflection angle was considered as the input and the UAV body attitude angle was considered as the output in the characteristic model. The attitude control law was raised by using linear golden section and nonlinear control method respectively. The attitude control law was proved to be stable and had no steady-state error by the simulation results. The nonlinear one is better in transient process and anti-interference ability. The demands are satisfied.
Key words:UAV; characteristic model; golden section; attitude control
【信息科学与控制工程】

