几何命题的极坐标证法

苏艳华

（沈阳大学师范学院，辽宁 沈阳 110044）

几何命题的证明一般常用综合法、解析法、向量法等等，这些方法各有所长，对于中学数学教师来说，掌握和运用这些不同的方法来证明几何命题十分必要.众所周知，极坐标是数学的有力工具，它主要用于解决几何中曲线方程，在几何教学、天体物理学中应用十分广泛，但目前国内中学数学教材介绍甚少，本文旨在通过具体实例介绍几何命题的极坐标证法，供大家分享之.

命题1 经过圆内任意一个定点作任意一条弦，则弦被这个点分得的两条线段的乘积是一个恒量.

证明 设P0为圆内任意一个定点，AB为经过P0的任意一条弦.采用极坐标系，以P0为极点，P0X为极轴.设圆的极坐标方程为

图1

这个方程可由圆的直角坐标一般式方程

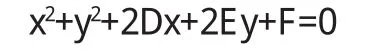
推导出来.弦AB的方程为

为了求出弦AB的两个端点的极径ρ1和ρ2的乘积（ρ2<0），以（2）代入（1），得

由韦达定理得

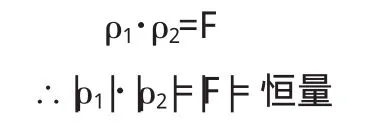
即|AP0|·|BP0|是一个恒量.

命题2 圆内接四边形的两组对边乘积的和等于两条对角线的乘积.

证明 采用极坐标系，以圆心O为极点，使极轴OX与P4P1相交.设顶点按逆时针方向依次为P1（r，θ1），P2（r，θ2），P3（r，θ3），P4（r，θ4），这里0<θi<2π，i=1，2，3，4.

图2

如图2，由正弦的定义，可知

由公式 cos（-x）=cosx，得

故本命题得证.

命题3 如图3，已知P是正三角形P1P2P3外接圆中劣弦上任意一个点，求证：

证明 采用极坐标系，以圆心O为极点，使P1在极轴OX上，则顶点为

图3

设 P点的坐标为（r，θ）则

命题4 由三角形外接圆上任意一个点分别对三角形三条边作垂线，则所得的三个垂足共线.

证明 设由△P1P2P3外接圆上任一点O分别作其三边的垂线，所得的三个垂足为F1，F2和F3.

采用极坐标系，取点O为极点，使△P1P2P3的外心在极轴OX上，则此外接圆的方程可写为

图4

三个顶点 P1，P2，P3的坐标依次为（2rcosθ1，θ1），（2rcosθ2，θ2），（2rcosθ3，θ3）

直线P2P3的方程可写为

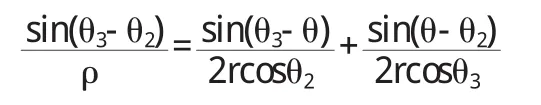
去分母，得

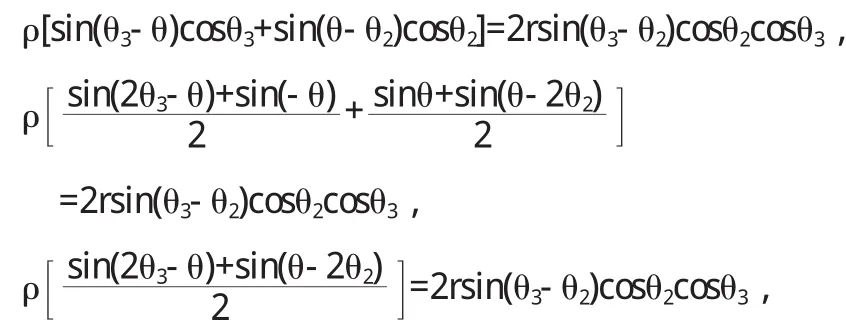
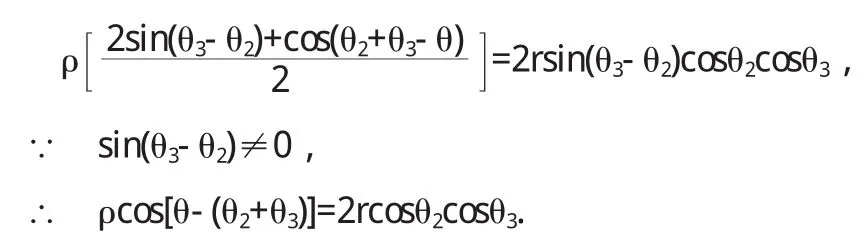
由此可知垂足 F1的坐标为（2rcosθ2cosθ3，θ2+θ3），同理，垂足 F2的坐标为（2rcosθ3cosθ1，θ3+θ1），垂足 F3的坐标为（2rcosθ1cosθ2，θ1+θ2）.

由验算可知三个垂足F1，F2，F3的坐标满足直线方程

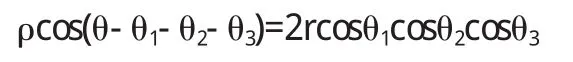
故 F1，F2，F3共线.

命题5 设经过两圆切点的两条直线交一个圆于A和B，交另一个 圆 于 C和 D，则AB//CD.

证明 采用极坐标系，取切点T为极点，使两圆的圆心在极轴TX上.设内切两圆的方程为

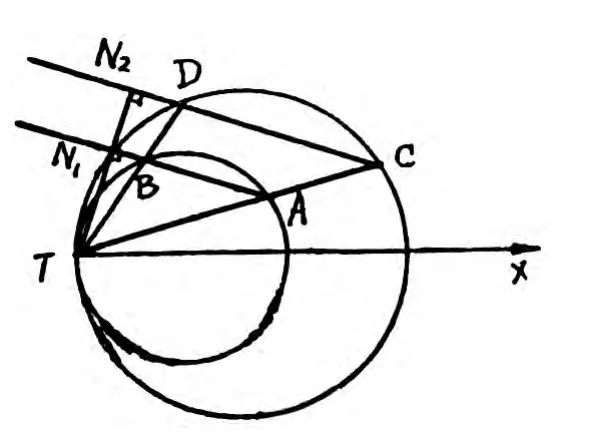
图5

经过切点T的两条直线的方程为

则 A点的坐标为（2r1cosα1，α1）,B点的坐标为（2r1cosα2，α2）,C点的坐标为（2r2cosα1，α1），D点的坐标为（2r2cosα2，α2）.

直线AB的方程为

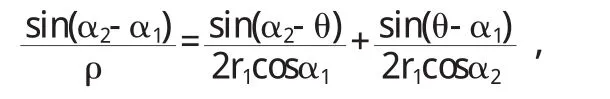
去分母，得

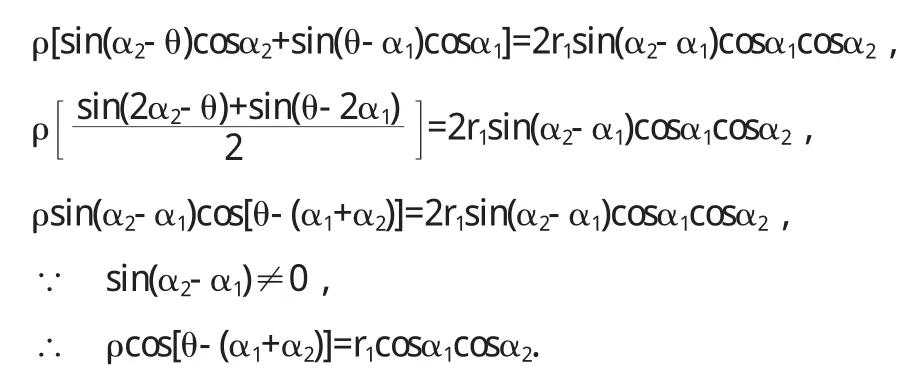
故直线 AB的法线角 ω1=α1+α2；

同理直线CD的法线角ω2=α1+α2.

∵ ω1=ω2，∴TN1和TN2在同一直线上，而AB和CD都与这条直线垂直，故AB//CD.

同样可证两圆外切时也有AB//CD.

命题6 设△ABC中∠A的平分线交BC于D，又交外接圆于 E，则 AB·AC=AD·AE.

证明 采用极坐标系，取A为极点，使△ABC的外心在极轴OX上，则外接圆的方程可写为

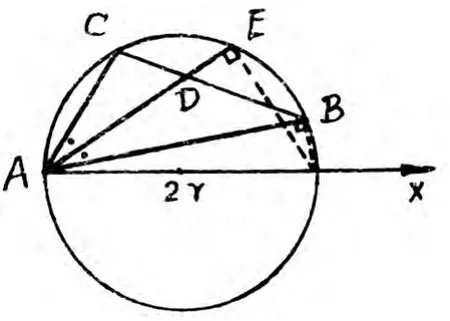
图6

设B，C的坐标分别为（ρ1，2θ1），（ρ2，2θ2），则 D，E的坐标可写为（ρ3，θ1+θ2），（ρ4，θ1+θ2）.

直线BC的方程为

因为点 D（ρ3，θ1+θ2）在直线 BC上，故有

（2）代入（1），得

命题7 三角形一条边上的高与外接圆直径的乘积等于其余两条边的乘积.

证明 采用极坐标系，取C为极点，使△ABC的外心在极轴CX上.设A，B的坐标依次为（ρ1，α），（ρ2，β），外接圆的方程为

直线AB的方程为

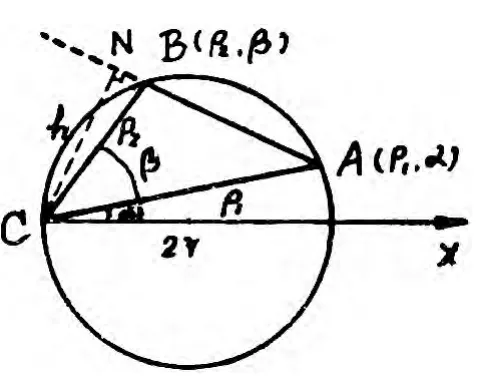
图7

去分母，得

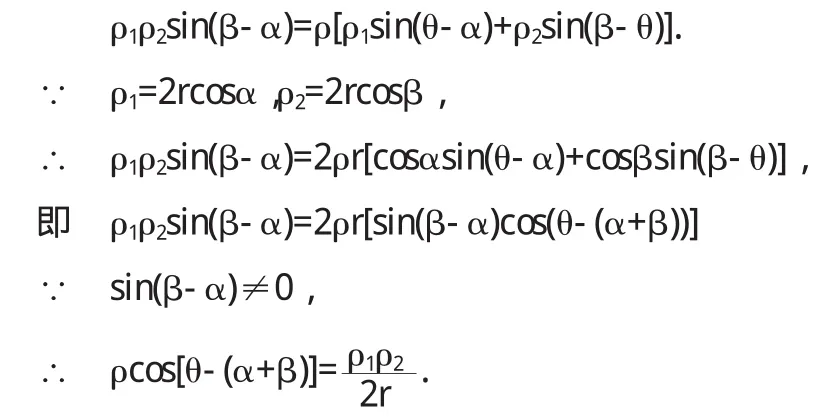
即 CN·（2r）=AC·BC.

命题8 由圆外一点所作切线的长是由它所作割线和这割线的圆外部分的比例中项.

证明 采用极坐标系以，圆外一点P为极点，使极轴通过圆心.设圆的方程为

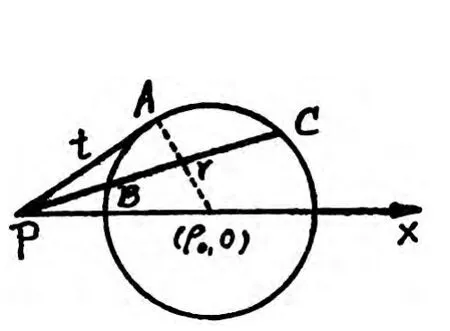
图8

割线PC的方程为θ=α，交点B和C的极径分别为ρ1和ρ2，由韦达定理可知

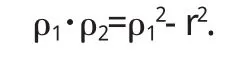
设切线长 PA=t2，则有

从而 ρ1：t=t：ρ2.

限于篇幅，仅举以上几例.研究极坐标在几何证题中的运用，既符合新课程标准的理念，又有利于开拓学生视野，并对提高学生解题水平、融汇贯通学科间的知识大有裨益.

〔1〕沈文选.平面几何证明方法全书[M].哈尔滨工业大学出版社，2005.

〔2〕肖维松.圆极坐标方程引理及其应用[J].新高考，2011（6）.

〔3〕于志洪.极坐标法证明四点共圆[J].厦门数学通讯，1982（1）.