一种基于五次CVC和SmartCrown复合辊型的板形控制方法

一种基于五次CVC和SmartCrown复合辊型的板形控制方法

唐忠李文强陶冶

四川大学，成都，610065

摘要：为改善轧机的板形调控能力，在分析连续变凸度CVC辊型和SmartCrown辊型特性的基础上，提出了一种基于五次CVC和SmartCrown的复合辊型的板形控制方法。将五次CVC和SmartCrown辊型在控制板形缺陷方面的特性相结合，采用分解与迭加的方法重新确定其二次和四次凸度及调控能力。通过设计实例和效果分析验证，表明该方法有效改善了五次CVC和AVC辊型因辊径差较大不利于板形控制的缺点。

关键词：复合辊型；板形控制；凸度；分解；迭加

中图分类号：TG333；TH122

收稿日期：2015-02-04

基金项目：科技部创新方法工作专项(2013IM030500，2013IM020400)；四川省科技支撑计划资助项目(2014GZ0124)；四川省科技基础条件平台项目(2013JCPT007)

作者简介：唐忠，男，1987年生。四川大学制造科学与工程学院硕士研究生。主要研究方向为机电系统创新设计。李文强(通信作者)，男，1976年生。四川大学制造科学与工程学院副教授。陶冶，男，1984年生。四川大学制造科学与工程学院讲师、博士。

A Method for Composite Roll Profile Control Based on Quintic CVC and SmartCrown

Tang ZhongLi WenqiangTao Ye

Sichuan University,Chengdu,610065

Abstract:In order to improve the profile control capability of rolling mill,based on the analyses of characteristics of continuously variable crown(CVC) roll contour and SmartCrown roll contour,a method for composite roll profile control was proposed based on quintic CVC and SmartCrown.Combined with the characteristics of quintic CVC and SmartCrown in the control of profile defects,these methods of decomposition and superposition were used to redefine its quadratic crown and quartic crown and control capability.Through the design example and result analyses,it demonstrates that the method effectively improves the disadvantages of profile control due to the larger roller diameter difference to the quintic CVC and advanced variable crown(AVC) roll contour.

Key words:composite roll;profile control;crown;decomposition;superposition

0引言

CVC辊型和SmartCrown辊型在板形控制领域中是较为理想的技术,CVC辊型的主要特点是把上下工作辊磨削成相同的S形，但反向180°装辊，使形成的辊缝轮廓形状对称，上下辊进行等量轴向移动，能对CVC工作辊凸度进行无级连续调节，SmartCrown辊型技术原理与CVC辊型技术相似。

近年来，国内外许多学者对不同辊型曲线及板形控制进行了研究。刘光明等[1]推导了包含轧件宽度的等效凸度表达式，改进了等效凸度的确定方法。张清东等[2]运用有限元解决了辊间接触压扁变形的建模问题，实现了对较复杂变形的求解。Zhang等[3]采用有限元方法建立了非对称板形的控制策略。白振华等[4]提出一套VC辊内辊型优化设计方案。Wang等[5]分析了工作辊窜动时对工作辊与支撑辊以及工作辊与带钢之间轴向力的影响。Shan等[6]建立的板形集成控制模型具有较高的板形控制精度。孔繁甫等[7]定义了一种以分段函数为表达式的MVC辊型。上述研究工作都为不同辊型及板形控制方法进行了有益探索。

李洪波等[8-9]研究表明，三次CVC辊型不具备四次凸度控制能力，SmartCrown辊型具有四次凸度控制能力，但控制能力受凸度比的影响。五次CVC辊型和AVC辊型[10]在轧制区域辊径差较大，常导致轧辊线速度差(轧辊与轧件在前滑区内的速度差)较大，轧制时板形不稳定。板形可分为对称板形与非对称板形，其控制方法有所不同。目前国内外对非对称板形调控多是采用非对称调控功效技术，如轧辊倾斜技术和非对称弯辊技术等。而对称板形缺陷又包括两类：第一类是与低次部分有关的二次缺陷(中间浪和双边浪)；第二类是与高次部分有关的四次缺陷(边中浪和四分浪)。仅对中间浪和双边浪进行控制已经不能满足高精度板带材产品的质量需求，对复合浪形(边中浪和四分浪)即对辊缝四次凸度的控制已成为一种趋势。基于此，本文在分析五次CVC和SmartCrown辊型曲线及控制板形缺陷的基础上，提出一种基于五次CVC和SmartCrown的复合辊型，并研究其对板形的控制特性。

1S形辊型曲线

在诸多学科的研究中，观察数据点图，经常会出现S形曲线，最简单且最常见的S形曲线有两种：第一种是三次方曲线，第二种是正弦曲线，其表达式分别为

y=ax3+bx2+cx+d

(1)

y=asin(bx+c)

(2)

冷轧中广泛使用的辊型曲线(轧辊轮廓函数或表面母线)是在式(1)和式(2)的基础上进行相应的改进得到的。以图1所示的CVC辊型工作辊辊身左端面为坐标原点建立坐标系，L为辊身长度，B为轧件宽度，D为上下两辊轴线间的距离，yu0(x)为上辊半径函数，yd0(x)为下辊半径函数。工作辊的半径沿辊身长度方向是变化的，辊型半径函数方程可用一个通式表示：

y(x)=a0+a1x+a2x2+…+aixi

(3)

i=1,2,…

其中，i=3，5时分别表示三次、五次CVC辊型。SmartCrown辊型曲线可定义为线性函数和正弦函数的迭加，半径函数可表示为

(4)

式中，x为辊身坐标；s0、ai为辊型系数；α为形状角。

图1　CVC辊型

根据CVC辊型上下工作辊的反对称性知，上工作辊辊型曲线半径函数为

yu0(x)=a0+a1x+a2x2+…+aixi

(5)

下工作辊辊型曲线半径函数为

yd0(x)=yu0(L-x)=a0+a1(L-x)+

a2(L-x)2+…+ai(L-x)i

(6)

当上辊右移s、下辊等距左移s时，辊缝中间高度变小，相当于轧辊等效凸度增加，此时称为正凸度(图2a)；反之称为负凸度(图2b)。横移s后上下工作辊辊型曲线半径函数分别为

yu(x)=yu0(x-s)

(7)

yd(x)=yd0(x+s)=yu0(L-x-s)

(8)

辊缝函数g(x)与CVC辊型函数之间的关系为

g(x)=D-yu(x)-yd(x)

(9)

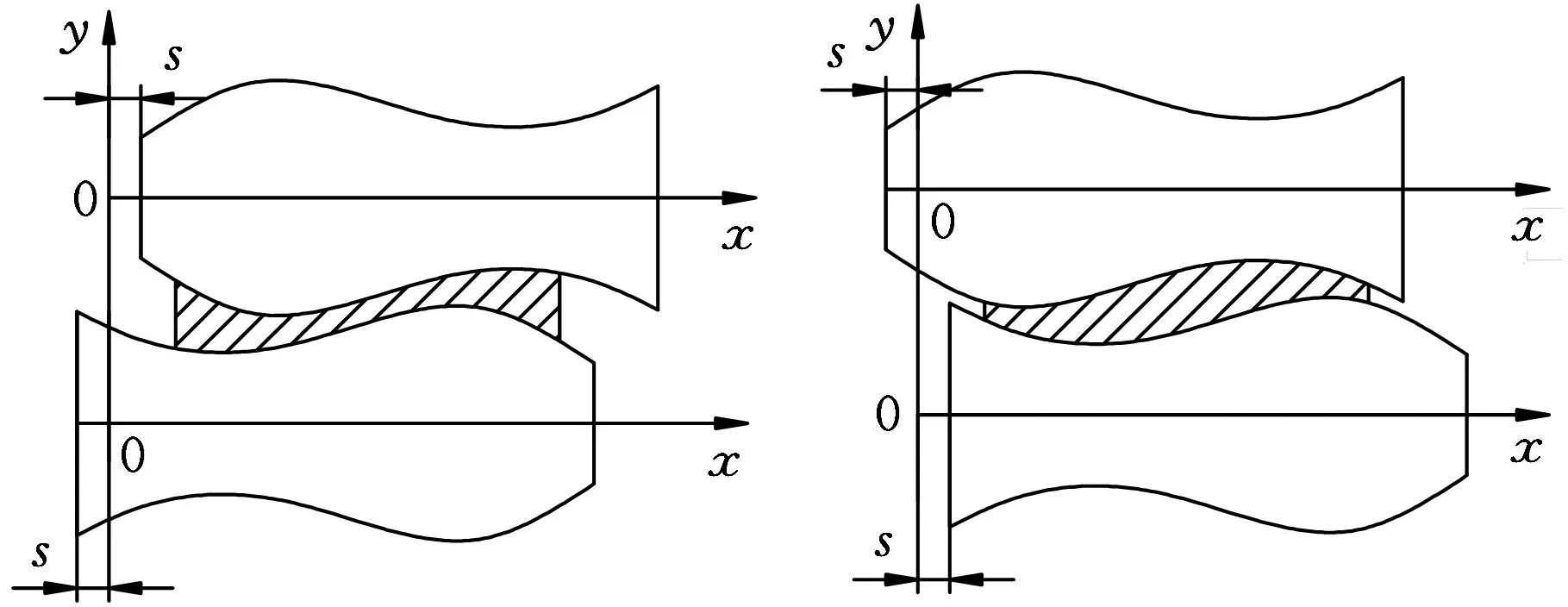
(a)正凸度(b)负凸度 图2　CVC轧辊窜动示意图

在分析三次CVC和五次CVC及SmartCrown辊型参数与辊缝凸度之间关系的基础上，得到三种组合式复合辊型：第一种为三次CVC和五次CVC多项式的迭加，显然迭加后仍为五次CVC辊型；第二种为三次CVC和SmartCrown辊型的迭加，即文献[10]提出的AVC辊型；第三种为本文将要探讨的基于五次CVC和SmartCrown的复合辊型。

2五次CVC、SmartCrown辊型特性分析

辊缝二次凸度和四次凸度分别由下式计算：

Cw=g(L/2)-g(0)

(10)

(11)

但实际计算时若直接按照式(10)、式(11)计算二次凸度和四次凸度，过程势必变得复杂。本文充分利用低次和高次辊缝函数结构之间的关系，提出采用分解与迭加原理计算凸度，计算量可大为降低。分解可描述为将复合辊型半径函数分解成五次部分(包括三次部分和高次部分)和正弦部分；迭加可描述为对分解后的各部分函数分别“计算”二次、四次凸度，最后迭加即为所求凸度。

2.1SmartCrown辊型特性

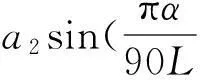
2.2五次CVC辊型特性

因传统的三次CVC辊型对板形的研究都是以二次板形为对象，容易得到三次CVC辊型辊缝二次凸度为

(12)

根据上文的分析，同样可将五次CVC辊型辊缝二次凸度分解为三次CVC辊型的二次凸度与高次项a4x4+a5x5产生的二次凸度的迭加。现只需对高次项a4x4+a5x5产生的二次凸度进行推导，原理与三次CVC辊型相同，下式为其二次凸度：

(13)

经迭加，五次CVC辊型辊缝二次凸度为Cw=Cw3+Cw45。因为三次CVC辊型辊缝四次凸度Ch3=0，所以五次CVC辊型的四次凸度只能由高次项a4x4+a5x5产生，其四次凸度为

(14)

3基于五次CVC和SmartCrown的复合辊型

3.1复合辊型的提出

基于上述分析，将五次CVC辊型和SmartCrown辊型在控制板形缺陷方面的特性相结合，并以式(3)和式(4)为基本方程，经迭加可初步定义基于五次CVC和SmartCrown的复合辊型半径函数为

y(x)=a0+a1x+a2x2+a3x3+a4x4+

(15)

3.2复合辊型特性分析

将复合辊型半径函数式(15)分解为如下形式：

(16)

显然，通过分解后各部分的二次、四次凸度将是“已知”的，迭加后二次凸度为

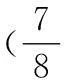
(17)

四次凸度为

(18)

对于相同的横移位置，不同宽度的带钢所对应的凸度值是不同的，所以应该考虑带钢宽度的轧辊等效凸度[1]，当带钢宽度为B时，实际二次凸度为

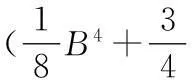
(19)

在给定窜辊范围[-sm,sm]时，可进一步得到实际的二次凸度调控能力：

ΔCwbf=3B2sma3+6LB2sma4+

(20)

3.3辊型系数确定

根据文献[8-9]，当形状角α≤180°时，其高次凸度控制能力不能得到充分发挥。为此，还需对式(15)做进一步改进，取s0=L/2，α=360°。则式(15)变为

y(x)=a0+a1x+a2x2+a3x3+a4x4+

(21)

为确定式(21)中的辊型系数s0，a0，a1，a2，a3，a4，a5，a6，理论上需要建立8个方程，但首先容易确定系数s0和a0。式(17)和式(18)表明，复合辊型的二次和四次凸度均与辊型系数a0、a1无关，这与对式(4)的推导认为线性部分二次凸度为零相吻合。a0只取决于轧辊的初始半径，即当式(21)中x=0时y(0)的值，故可设为一已知量。

其次确定辊型系数a1～a6，现在只需建立6个方程。因为对于复合轧辊来说，存在一定的辊径差ΔD是必要的，但ΔD又不能过大，否则会对轧机设备结构造成影响，破坏正常的工艺条件。此外，较小的ΔD有利于减小带钢的残余应力，改善带钢质量，因此首先通过轧辊辊径差ΔD=0建立一个关于a1,a2,…,a6的方程：

(22)

类似于处理第一类边值问题的方法，容易建立其余5个方程，同时需要给定第一类边值条件：轧辊轴向的窜辊范围[-sm,sm]，以及对应的二次凸度范围[Cwbf1,Cwbf2]和四次凸度范围[Chf1,Chf2]，则根据式(18)和式(19)式得到关于a2,a3,…,a6的两个方程组共四个方程:

(23)

(24)

若进一步给定边值条件：可轧宽度范围[Bmin,Bmax]，并令轧制最窄及最宽带钢时具有相同的二次凸度调控能力ΔCwbf，则由式(20)可得到一个关于a3～a6的方程:

ΔCwbf=f(a3,a4,a5,a6,Bmin,sm)=

f(a3,a4,a5,a6,Bmax,sm)

(25)

最后根据式(22)～式(25)(共6个方程)可唯一确定辊型系数a1～a6，此时辊型系数s0、a0～a6完全确定，复合辊型半径函数式(21)也唯一确定。

4设计实例与效果分析

设计参数如表1所示，辊型系数计算结果如表2所示。特别地，若当复合辊型曲线表达式(21)中的a6=0时，复合辊型就为五次CVC辊型。若a4=a5=0时，复合辊型就为AVC辊型。

表1　设计参数　mm

表2　辊型系数计算结果

复合辊型、五次CVC辊型和AVC辊型曲线(轧辊半径与初始点y(0)=a0的相对差值)对比如图3所示。在轧制区域中部，辊径差的大小顺序依次为：五次CVC辊型>AVC辊型>复合辊型，该差值越大将导致轧辊产生线速度差(轧辊与轧件在前滑区内的速度差)越大，从而使五次CVC辊型和AVC辊型对板形控制不稳定，而与五次CVC辊型和AVC辊型相比复合辊型减小了中部辊径差，轧制板带时较稳定。

图3　不同辊型曲线对比

复合辊型同时具有二次、四次凸度，如图4所示，其中二次凸度与窜辊位置表现为强烈的线性关系，虽然四次凸度有极小波动，但也可以近似认为与窜辊位置成线性关系，在窜辊量为零时二次和四次凸度均趋于零，但不等于零。该特性对控制板形的复合浪形(边中浪和四分浪)是有利的。

图4　复合辊型辊缝凸度

复合辊型、五次CVC辊型和AVC辊型的二次凸度调控能力随带钢宽度的变化如图5所示，若带钢宽度B从2000mm降到1250mm时，则其各自的调控能力随带钢宽度下降的百分比依次为：五次CVC辊型68.4%>AVC辊型48.1%>复合辊型26.0%，表明随带钢宽度的减小，复合辊型的调控能力不仅下降平缓，而且对窄带钢仍有富裕的二次凸度调控能力，即复合辊型在宽带钢轧机上应用时同时具备控制窄带钢的二次凸度控制能力。

图5　不同带钢宽度的二次凸度调控能力

若分别取四次凸度变化范围Δ=Chf2-Chf1为0.5,0.3,0.1,-0.1,-0.3,-0.5mm，则复合辊型二次凸度调控能力随带钢宽度变化表现出的不同特性如图6所示。因为，当四次凸度Chf2-Chf1<0且Chf2-Chf1越小时，复合辊型的实际二次凸度调控能力曲线呈凹函数，所以二次凸度调控能力在轧制区域随带钢宽度减小而迅速下降。而当四次凸度Chf2-Chf1>0时，二次凸度调控能力曲线呈凸函数，二次凸度调控能力在轧制区域随带钢宽度减小而下降的趋势有所变缓。但Chf2-Chf1越大时凸状越明显，此时二次凸度调控能力在轧制区域随带钢宽度减小亦迅速下降。

图6　不同四次凸度范围下二次凸度调控能力

若分别取二次凸度变化范围Δ=Cwbf2-Cwbf1为-0.6,-2.0,-4.0mm，则复合辊型辊缝四次凸度随窜辊位置而变化的特性如图7所示，虽然Cwbf2-Cwbf1越小时辊缝四次凸度与窜辊位置之间的函数关系越偏离线性关系，但该变化是轻微的。此时(甚至当Cwbf2-Cwbf1=-4.0mm时)辊缝四次凸度与窜辊位置仍然可以近似成线性关系，只是二次凸度变化范围越小时线性关系越强。

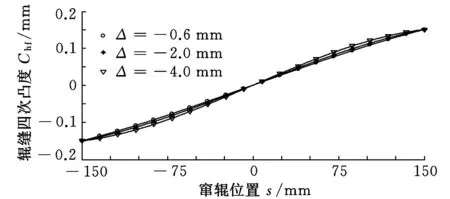
图7　不同二次凸度范围下的辊缝四次凸度

综上分析表明，在二次凸度调控范围确定的同时，就在一定程度上限制了四次凸度的调控范围，且在二次凸度范围确定的情况下，四次凸度范围不宜过大，通常四次凸度范围小于二次凸度范围。

5结论

本文提出了一种基于五次CVC和SmartCrown复合辊型的板形控制方法，采用分解与迭加方法重新确定了其二次和四次凸度及凸度调控能力。复合辊型与五次CVC辊型和AVC辊型相比能获得较小的辊径差。在不同的二次凸度范围下，辊缝的四次凸度与窜辊位置之间的函数关系可近似为线性关系。该复合辊型在宽带钢轧机上应用时对窄带钢同样具有富裕的二次凸度调控能力，可获得较好的板形控制效果。

参考文献：

[1]刘光明，邸洪双，常安，等.CVC轧机辊形曲线设计及等效凸度探讨[J].东北大学学报(自然科学版)，2008，29(10):1443-1446.

LiuGuangming，DiHongshuang，ChangAn，etal.DiscussiononDesignofCVCRollProfileandItsEquivalentCrown[J].JournalofNortheasternUniversity(NaturalScience)，2008，29(10):1443-1446.

[2]张清东，孙向明，白剑.六辊CVC轧机辊系变形的有限元分析[J].中国机械工程，2007，18(7):789-792.

ZhangQingdong，SunXiangming，BaiJian.AnalysisofRolls’ElasticDeformationonCVC6 -hMillbyFEM[J].ChinaMechanicalEngineering，2007，18(7):789-792.

[3]ZhangYun，YangQuan，WangXiaochen.ControlStrategiesofAsymmetricStripShapeinSix-HighColdRollingMill[J].JournalofIronandSteelResearch，International，2011，18(9):27-32.

[4]白振华，王凯，王亚军，等.VC轧机内辊型优化设计技术的开发[J].中国机械工程，2013，24(22):3096-3100.

BaiZhenhua，WangKai，WangYajun，etal.InnerRollShapeOptimizationDesignTechnologyofVCMill[J].ChinaMechanicalEngineering，2013，24(22):3096-3100.

[5]WangJS，JiangZY，TieuAK，etal.AnalysisofThrustForceinaWorkRollShiftingMill[J].InternationalJournalofMechanicalSciences，2006，48(10):1095-1102.

[6]ShanXiuying，LiuHongmin，JiaChunyu，etal.FlatnessandProfileIntegrationControlModelforTandemColdMills[J].JournalofIronandSteelResearch，International，2012，19(3):31-37.

[7]孔繁甫，何安瑞，邵健，等.板带轧机工作辊混合变凸度辊形研究[J].机械工程学报，2012，48(22):87-92.

KongFanfu，HeAnrui，ShaoJian，etal.ResearchonMixedVariableCrownContourforWorkRollofStripMill[J].JournalofMechanicalEngineering，2012，48(22):87-92.

[8]李洪波，张杰，曹建国，等.三次CVC、五次CVC及SmartCrown辊形控制特性对比研究[J].中国机械工程，2009，20(2):237-240.

LiHongbo，ZhangJie，CaoJianguo，etal.ControlCharacteristicsContrastamongCubicCVC,QuinticCVCandSmartCrownRollContours[J].ChinaMechanicalEngineering,2009,20(2):237-240.

[9]李洪波，张杰，曹建国，等.五次CVC工作辊辊形与板形控制特性[J].机械工程学报，2012，48(12):24-30.

LiHongbo，ZhangJie，CaoJianguo，etal.RollContourandStripProfileControlCharacteristicsforQuinticCVCWorkRoll[J]．JournalofMechanicalEngineering，2012，48(12):24-30.

[10]李洪波，张杰，曹建国，等.先进变凸度工作辊辊形及其控制特性[J].北京科技大学学报，2011，33(11):1402-1405.

LiHongbo，ZhangJie，CaoJianguo，etal.AdvancedVariableCrownWorkRollContourandItsCrownControlCharacteristics[J].JournalofUniversityofScienceandTechnologyBeijing，2011，33(11):1402-1405.

(编辑苏卫国)