单模复合功率分流混合动力系统结构优化

单模复合功率分流混合动力系统结构优化

杜爱民1刘开圣1朱忠攀1王晨1,2

1.同济大学,上海,2018042.吉利电子传动技术有限公司,上海,201501

摘要：针对混合动力汽车中的动力耦合系统,提出一种双行星排结构的单模复合功率分流装置。通过对几种方案机械点的特性进行分析,筛选得出最优结构。对行星排特征参数进行优化,并推导得出满足结构限制的参数条件范围,在此基础上分析系统的工作模式和控制策略,最终利用离线仿真对该方案进行验证。

关键词:复合功率分流;单模;混合动力变速箱;机械点

中图分类号：U463.212.2

收稿日期：2014-10-16

作者简介:杜爱民,男,1971年生。同济大学汽车学院副教授。主要研究方向为汽车节能与排放控制、混合动力汽车系统集成控制。刘开圣，男，1990年生。同济大学汽车学院硕士研究生。朱忠攀，男，1988年生。同济大学汽车学院博士研究生。王晨，男，1986年生。同济大学汽车学院博士研究生，吉利电子传动技术有限公司工程师。

Structure Optimization of Single-Mode Compound Split Hybrid Power Train

Du Aimin1Liu Kaisheng1Zhu Zhongpan1Wang Chen1,2

1.Tongji University,Shanghai,201804

2.Geely Electric Transmission Technology Co., Ltd.,Shanghai,201501

Abstract:Based on a power coupling system in hybrid vehicles,a novel single-mode compound split power train with the structure of double-row planetary gear sets was proposed.An optimized structure was obtained by analyzing the mechanical points.Then the range of characteristic parameter of the planetary gear set was calculated and optimized.Operating modes and control strategy were analyzed based on this optimized structure.The effectiveness of this hybrid system was finally validated by the simulation.

Key words:compound power split;single-mode;hybrid gear box;mechanical point

0引言

目前,混合动力汽车的主要结构形式分为串联式、并联式和混联式。混联式又称为功率分流式(power split),采用行星齿轮排机构,实现发动机转矩与转速同车轮转矩与转速的解耦[1],因此可使发动机工作在经济区间内。

根据功率分流的方式及行星排的数量,功率分流式混合动力汽车可分为输入分流式(input split)、输出分流式(output split)和复合分流式(compound split)[2]。其中,输入分流是通过行星排将发动机输出功率在混动系统的输入端进行一次分流；输出分流是通过行星排将发动机剩余功率和驱动电机功率在混动系统的输出端进行一次汇流；复合分流则是通过行星排将发动机输出功率进行分流，同时又利用行星排在输出端对来自不同路径的功率进行汇流。

相比输入分流与输出分流式系统，复合分流式系统通常是由两组行星齿轮排组成的四轴结构。由于两个电机均不与发动机和输出轴直接相连，故两电机转速均可为零，即电功率分流比例为零，系统可以得到两个机械点[3],其高效率区间得到扩展。复合分流式系统在双模混合动力汽车中已得到广泛应用，如通用汽车公司2001年推出的AHS混合动力系统就是一种利用多行星排[4],既能实现输入功率分流又能实现复合功率分流的双模传动方案。

AHS系统需要多个离合器以控制模式切换，机械结构极其复杂，成本较高。因此本文提出一种基于拉维娜式行星齿轮机构的单模复合功率分流装置。通过机械点的特性分析对方案结构进行筛选，并对可行方案进行行星排特征参数优化,分析了系统的工作模式和控制策略，最后利用离线仿真对该方案的有效性进行验证。

1单模复合分流式系统设计

该单模复合分流装置[5]采用共用行星架和齿圈的双行星排结构,如图1所示。图1中,S1为前排轮系小太阳轮;P1为前排轮系短(粗)行星轮;P2为后排轮系长(细)行星轮;S2为后排轮系大太阳轮;C1为前后排轮系共用行星架;R1为前后排轮系共用齿圈。

图1　单模复合功率分流装置

1.1机械点与系统效率

采用杠杆法[6]对图1所示的结构进行等效,可得一个四轴式传动方案。图2为一种布置方案的杠杆结构图,图中,OUT表示输出轴,ENG表示发动机。设i1为前排行星齿轮传动比,i1=-ZR1/ZS1;i2为后排行星齿轮传动比,i2=ZR1/ZS2;ZR1、ZS1和ZS2分别为齿圈齿数和太阳轮S1、S2的齿数；同时设α为电机MG1到输出轴的杠杆长度与发动机到输出轴的杠杆长度之商;β为电机MG2到输出轴的杠杆长度与发动机到输出轴的杠杆长度之商。

图2　等效杠杆图

根据行星齿轮机构各部件运动规律可得如下两个转速平衡方程：

ωMG1=αωENG+ωO(1-α)

(1)

ωMG2=βωENG+ωO(1-β)

(2)

式中,ωMG1、ωMG2、ωENG、ωO分别为电机1、电机2、发动机和输出轴的角速度。

忽略各运动部件的角加速度，则由图2所示的杠杆模型可得到两个转矩平衡方程：

TENG+TMG1+TMG2+TO=0

(3)

TO+(1-α)TMG1+(1-β)TMG2=0

(4)

式中,TENG、TMG1、TMG2、TO分别为发电机、电机1、电机2、输出轴的转矩。

同时假设蓄电池净功率为零,则得到电功率平衡方程:

(5)

式中,ηMG1、ηMG2分别为电机1和电机2的效率。

由于电机在发电和电动工况下存在能量损失,故复合分流系统的传动效率为

(6)

式中,POUT、PENG分别为输出轴和发动机的输出功率。

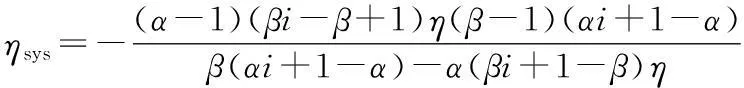
(7)

设两电机效率均为85%,则系统的传动效率随传动比i的变化曲线如图3所示。当系统效率达到最高值时,变速箱内部无电功率流动,输出功率全部由发动机直接提供，此时的传动比i称为系统的机械点(mechanical points)[7]。显然当电机1或电机2的转速为零时系统中的电功率为零，此时对应的传动比为系统的机械点，由此可计算复合分流系统的机械点传动比。

电机1转速为零时：

电机2转速为零时：

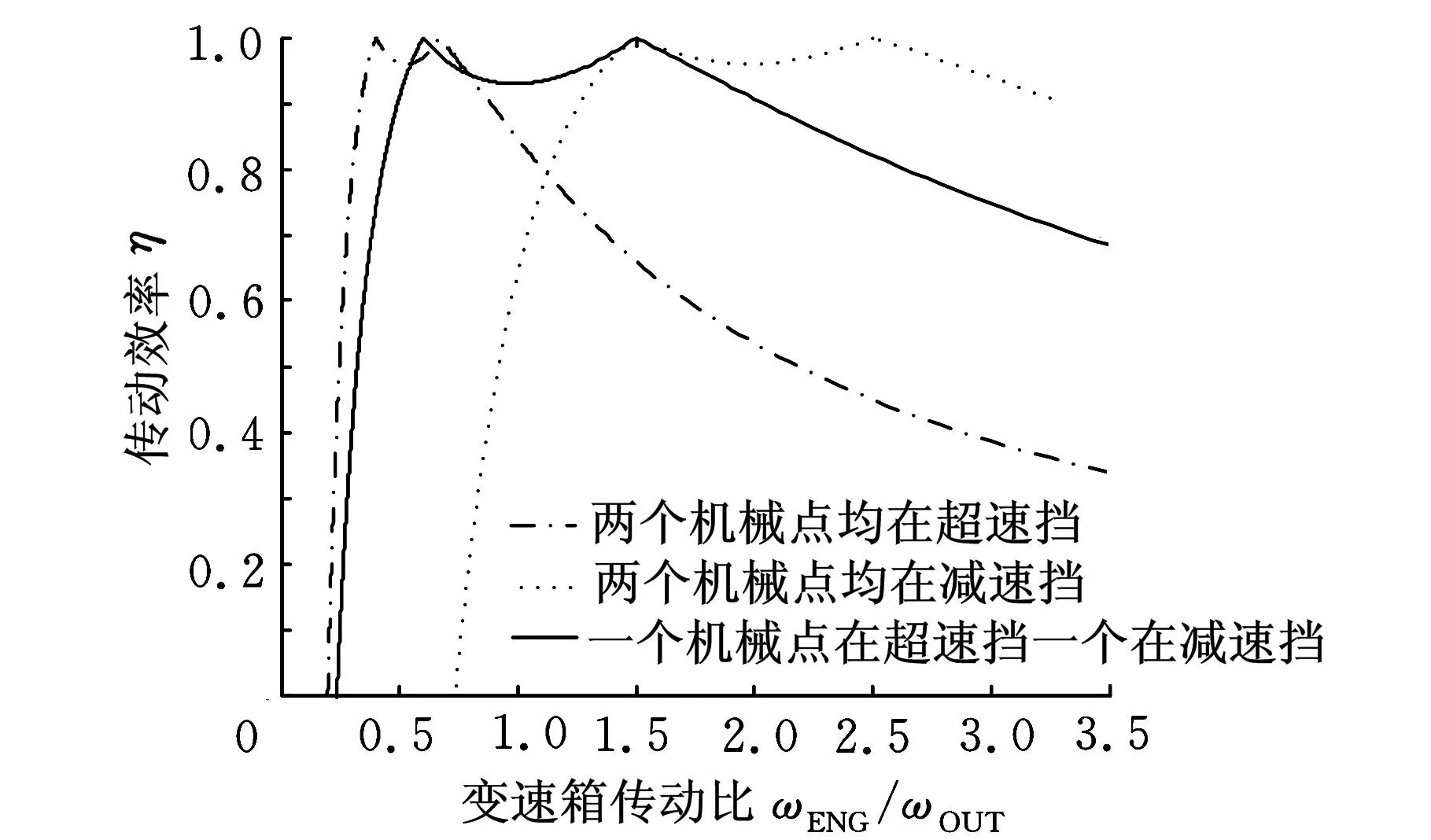
图3　系统传动效率

1.2系统方案筛选

由图3可知,该单模复合分流系统为四轴传动方案,而每轴均可与发动机、电机MG1、电机MG2、输出轴等4个部件中的一个相连,因此该四轴系统共有4!=24种布置方式。

定义传动比i>1为减速挡,00的区间内；②只有1个机械点落在i>0的区间内；③2个机械点均位于超速挡；④2个机械点均位于减速挡；⑤一个机械点位于超速挡，另一个位于减速挡。

由于机械点位置处传动效率最高,多个机械点可扩大系统的高效区间,故应从具有2个机械点的③、④、⑤类中选择布置方案。同时为了使该结构在城市工况与高速工况下均具有较高传动效率,应将2个机械点分别设置在减速挡和超速挡区间内,使高效区间尽可能覆盖到常用车速区间，所以选择第5类布置方式作为结构方案。

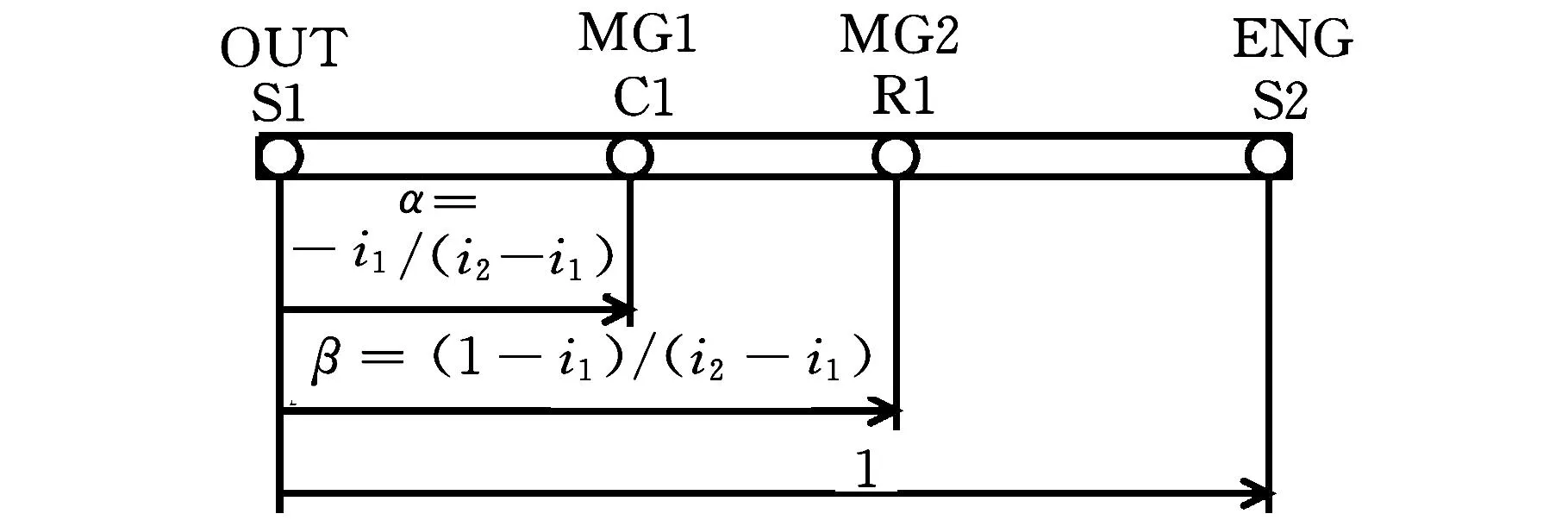
(a)2个机械点均未落在i>0的区间内

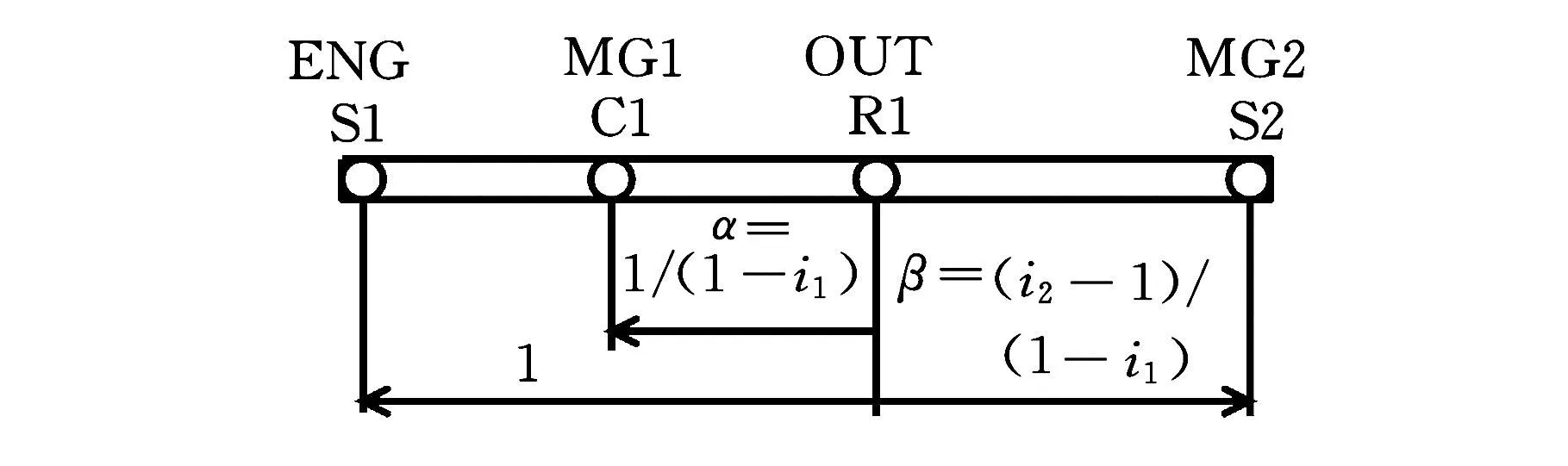
(b)只有1个机械点落在i>0的区间内

(c)2个机械点均在超速挡

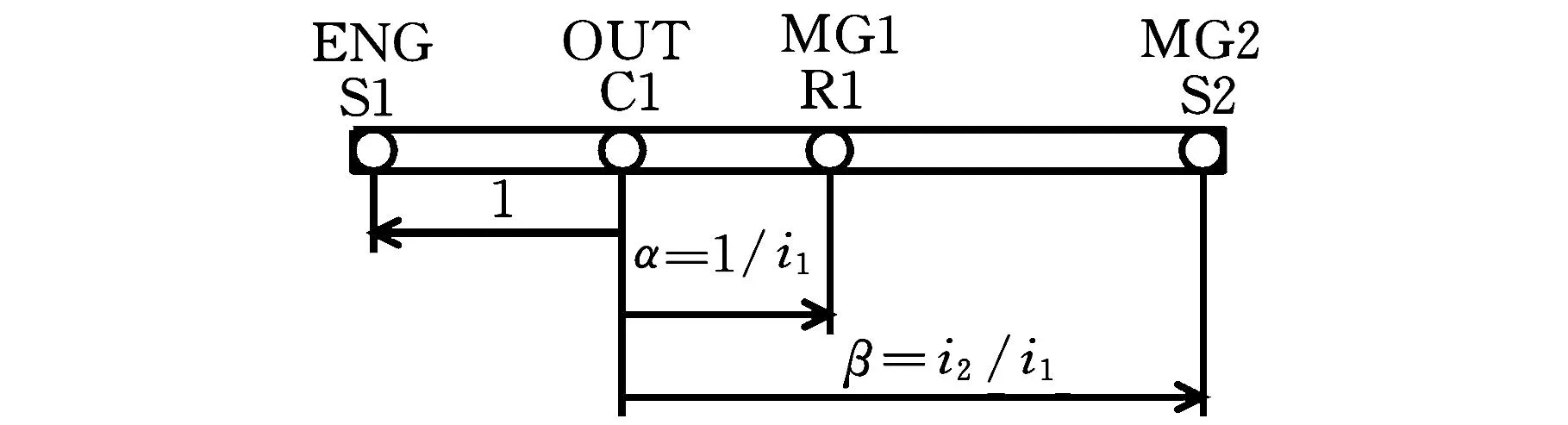
(d)2个机械点均在减速挡

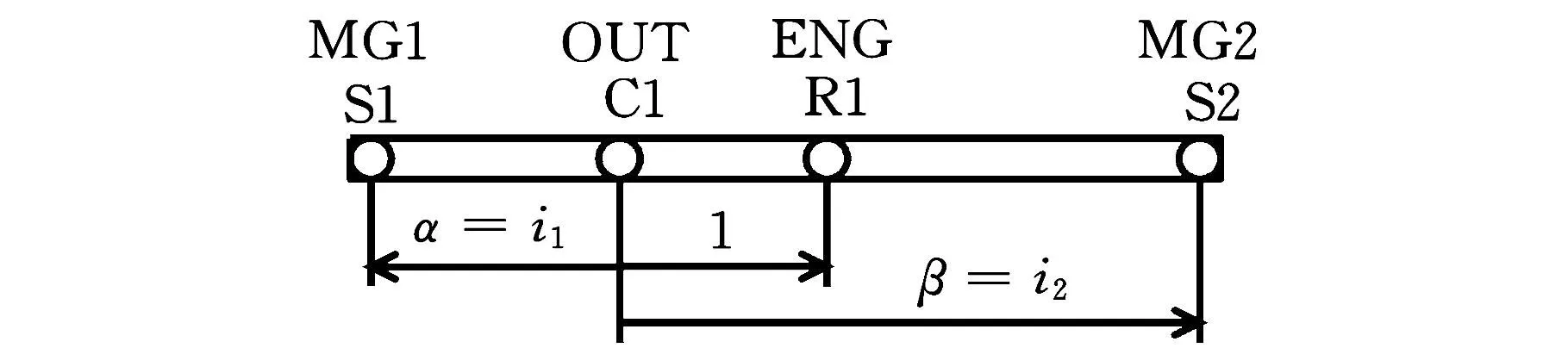
(e)一个机械点在超速挡，另一个在减速挡 图4　机械点分布特性

对于一个机械点在超速挡、一个在减速挡的方案,可有两种布置结构,其杠杆图见图5。

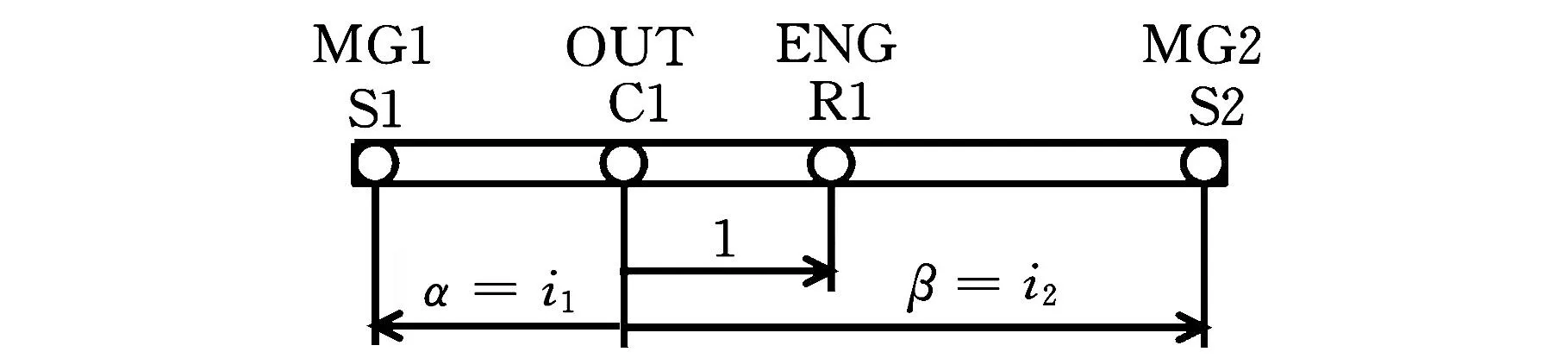
(a)方案a

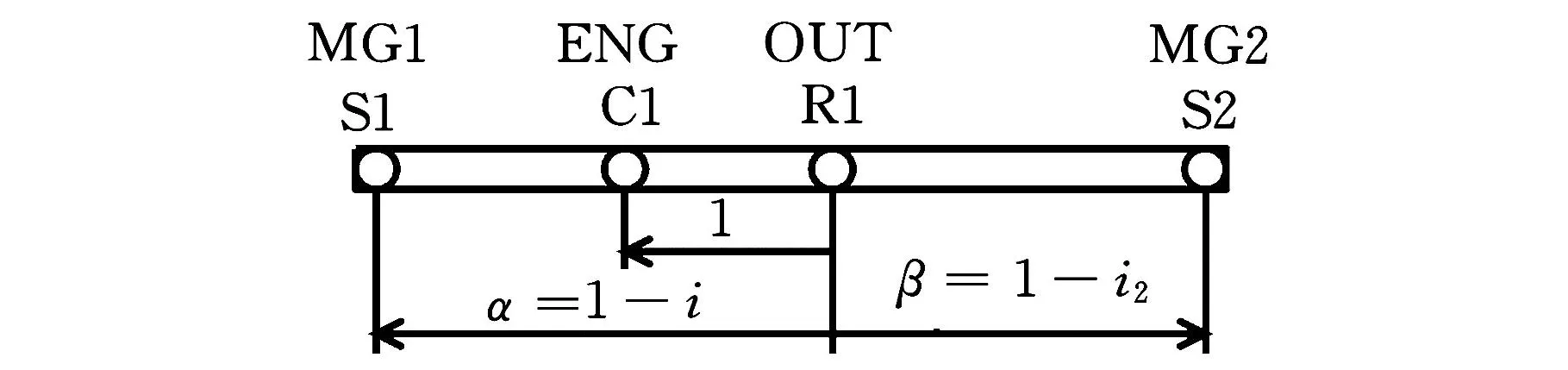
(b)方案b 图5　两种可行结构方案

设i1=-1.5,i2=3,Φ=PMG1/PENG；Φ为电机MG1与输入端电功率分流比;PMG1为电机MG1功率。Φ>0时电机MG1处于电动工况;Φ<0电机时MG1处于发电工况。则在两行星排特征参数相同的情况下，方案a与方案b的传动效率曲线较为接近,如图6所示。由图7所示的电功率分流比特性可知，对于方案a,传动比位于两机械点之间的高效区内时电机MG1处于电动工况,而在其他区域内则为发电工况;方案b中,电机MG1的工作状态正好与方案a相反。由此可知方案a中的电机MG1应布置为电动机，方案b中的电机MG1则应布置为发电机。因此，只要合理选择电机MG1的类型，方案a和方案b均可用于单模复合功率分流系统。

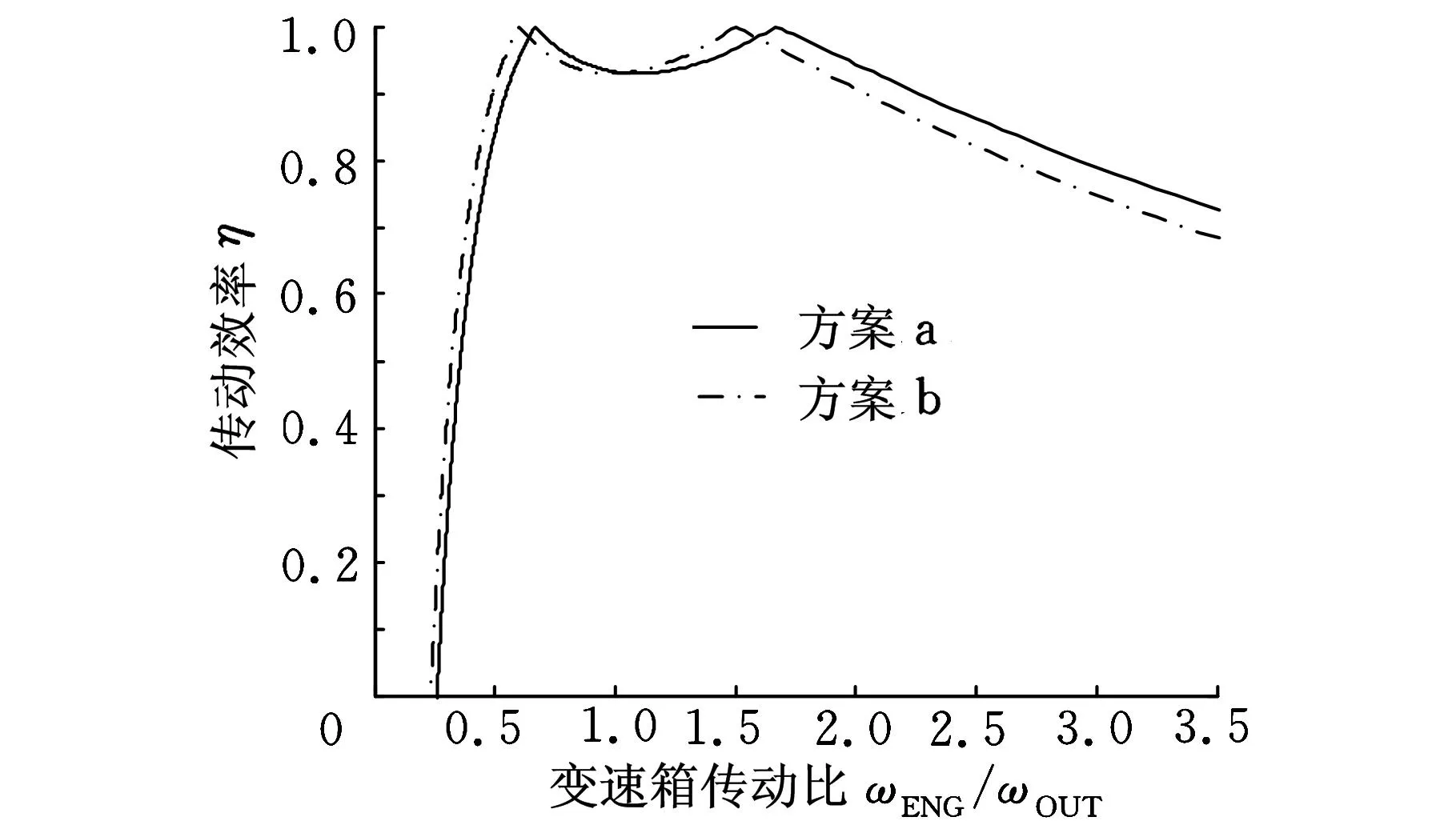
图6　两种可行方案传动效率

图7　两种可行方案电功率分流比

1.3行星排特征参数的确定

选取图5b所示的结构方案对前后排传动比i1、i2进行进一步的优化。

混合动力变速器应具有以下特点[8]:

(1)同一输出轴转速下(同一车速时)发电机应具有较宽的可调速范围,为发动机的工作状态提供较大的自由度，便于稳定工况时发动机的油耗和排放性能的优化。

(2)在同一发动机转速下,发电机应具有较宽的可调速范围。在一定的发动机转速下，发电机转速调节范围较宽，则短时间车速变化时，控制系统可以首先调节电机的功率满足动力系统需求，保证发动机工作状态稳定，从而降低发动机工作的不稳定性。

(3)常用车速下，内燃机的优化工作范围应该处于内燃机可调节的经济转速范围之内。

对于本结构的前后行星排，其前排太阳轮转速ωS1、齿圈转速ωR1、行星架转速ωC1、后排太阳轮转速ωS2满足下列关系：

ωS1+i1ωR1=(1+i1)ωC1

(8)

ωS2-i2ωR1=(1-i2)ωC1

(9)

因此前行星排中的输出轴转速、发动机转速和电机MG1转速可分别作为空间的x、y、z轴，由此确定一立方体；同理,由后行星排中的输出轴转速、发动机转速和电机MG2转速亦可确定一立方体，如图8所示。图中截面A即为该机构实际可达到的工作范围。由式(8)、式(9)可知，截面A的形状分别由i1和i2确定。

图8　转速平面关系图

在图8中可由a、c、h三点确定平面B，其在3个坐标平面内均具有较大的投影面积，满足前文所述混合动力变速器的要求，因此截面A的理想形状应为与截面B平行或接近平行，即两平面的法向量间的夹角θ应最小:

式中,(a1,a2,a3)为截面A的转速平面特征法向量；(b1,b2,b3)为截面B的转速平面特征法向量。

对于前行星排：

(a1,a2,a3)=(i1,-1-i1,1)

(b1,b2,b3)=(2/nomax,-3/nemax,1/nMG1max)

对于后行星排：

(a1,a2,a3)=(i2,1-i2,-1)

(b1,b2,b3)=(2/nomax,-3/nemax,1/nMG2max)

式中,nomax为输出轴正常工作的最高转速;nemax为发动机允许的最高转速;nMG1max和nMG2max分别为发电机和电动机的最高工作转速。

给定nomax=6300r/min,nemax=5500r/min,nMG1max=10 500r/min，nMG2max=8500r/min,则i1、i2与θ的关系如图9、图10所示，因此可得在i1=2.6时,θ有最小值0.1204rad;由图10可知,θ随i2的增大而单调递减，规定传动比1.5≤i≤3[9],则当i2=3时θ有最小值。

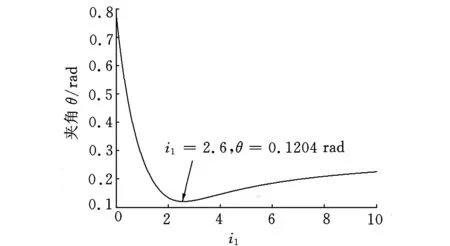
图9　i 1与θ关系

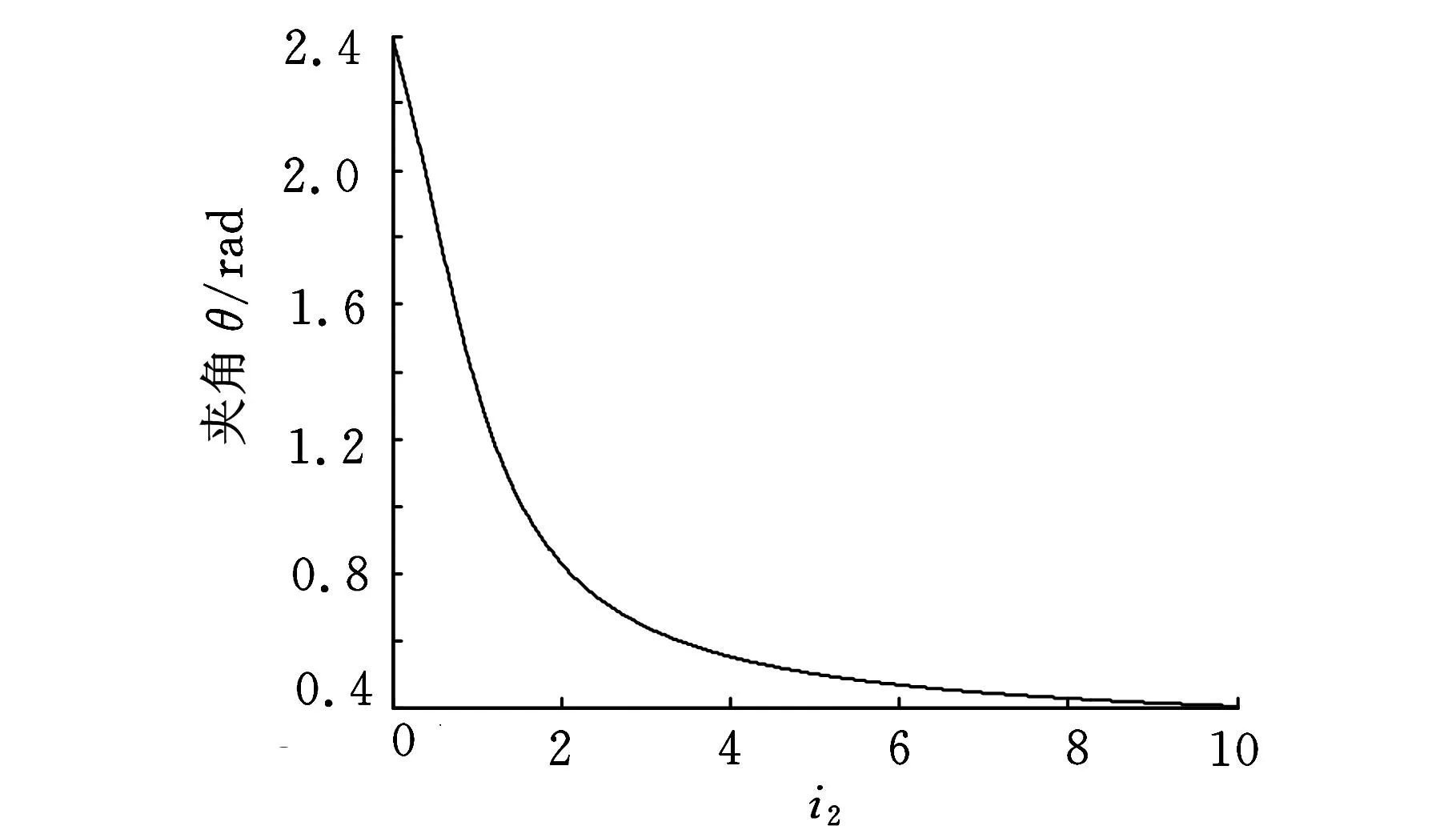
图10　i 2与θ关系

由于该系统采用双行星排的拉维娜结构,如图1所示,因此i1和i2的取值直接决定后排行星轮P2的位置与大小。为保证P2不与齿圈和相邻前排行星轮P1′发生干涉，同时又要满足齿轮的啮合要求，i1和i2需满足一定的限制条件。

设前后太阳轮的中心点均为坐标原点(0,0),前排行星轮P1的中心点为(x1,0),后排行星轮P2的中心点为(x,y),如图11所示，则根据啮合关系可得

(10)

(11)

式中，R为齿圈分度圆半径。

图11　拉维娜行星排结构图

为满足P2不与齿圈发生干涉，可推出

(12)

为满足P2不与行星轮P1′发生干涉，可推出

(13)

外啮合斜齿轮齿数比范围为1～15,可推出

(14)

将i1=2.6和i2=3代入式(10)～式(14)进行验证,计算结果均满足约束方程,因此i1和i2的取值符合结构要求,可选为本系统行星排的前后传动比。

2工作模式及控制策略

2.1纯电动模式

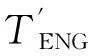
图12　纯电动模式

2.2发动机启动模式

当蓄电池SOC值小于系统设定的最低值，或驾驶员油门踏板信号对应的转矩需求值大于电动机对应转速下所能提供的最大转矩时，电机拖动发动机达到启动转速，发动机开始喷油工作。

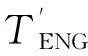
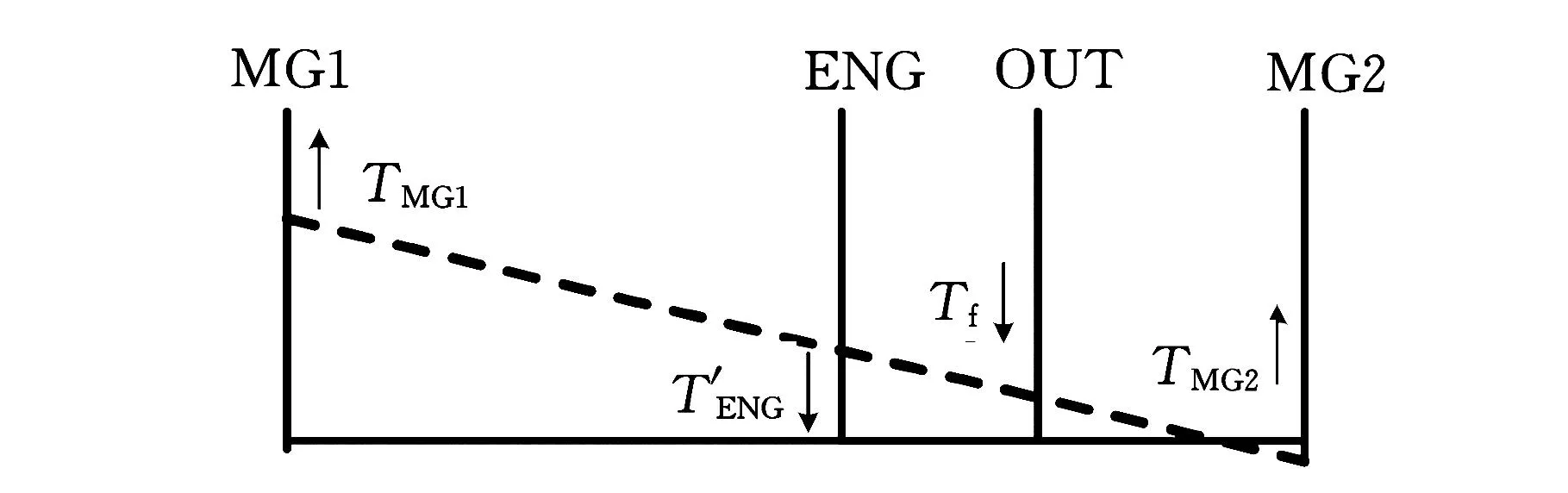
图13　发动机启动模式

2.3混合驱动模式

发动机启动后,根据蓄电池VSOC和附件消耗功率确定整车目标充电率；根据油门踏板信号确定需求功率，通过发电机MG1控制发动机转速，电动机MG2完成输出轴转矩补偿，使得发动机工作在燃油经济性最优区间内。

图14　混合驱动模式

2.4制动模式

驾驶员踩下制动踏板后,发动机迅速断油熄火，电机提供制动转矩,将汽车动能转换为电能储存到蓄电池中。但受到两电机转速及电池充电功率的限制，发动机MG1在高速制动时须提供平衡转矩对发动机的拖转工作点进行调整。而当制动需求超出混合动力系统所能提供的制动能力, 或电池SOC 值超过所允许的上限值时, 摩擦制动系统将进行辅助制动, 保证行车安全，其杠杆等效图见图15。

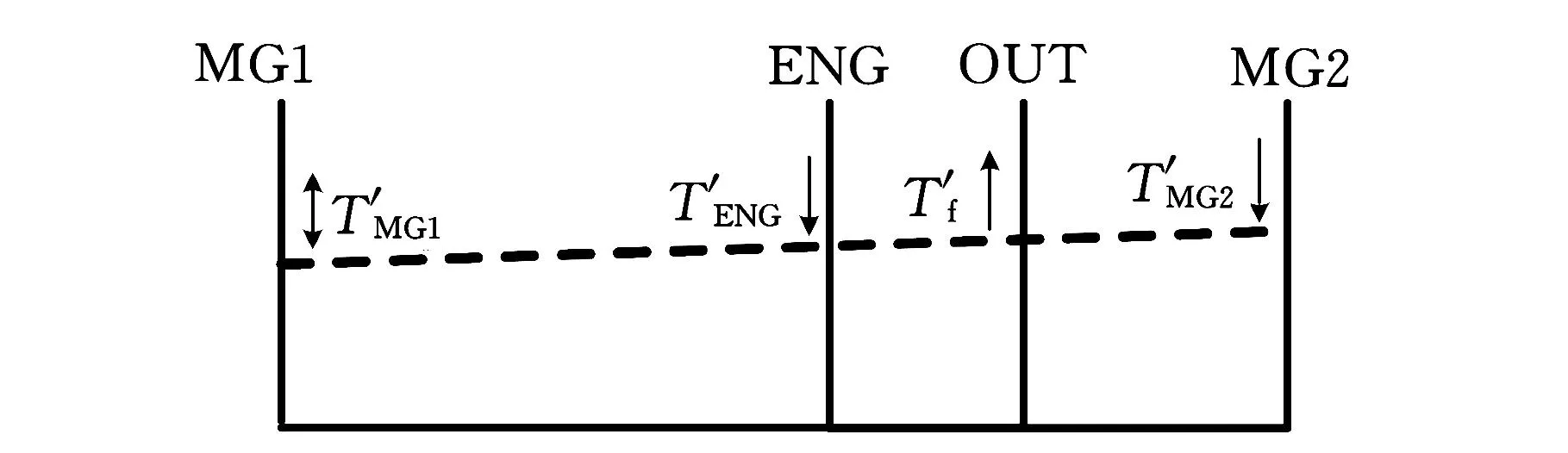
图15　制动模式

3离线仿真

确定行星排结构、前后行星排传动比及系统工作模式后,使用MATLAB对该混动系统进行NEDC工况下的油耗仿真。样车整车参数及各主要动力部件参数如表1、表2所示。蓄电池SOC值起始值为0.6,燃油经济性仿真结果如图16所示。

表1　整车参数

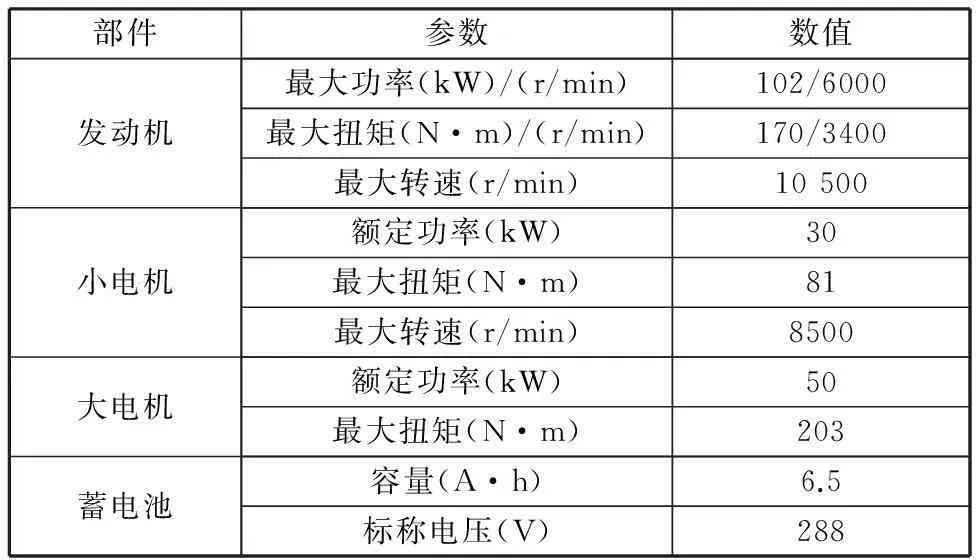
表2　各主要动力部件参数

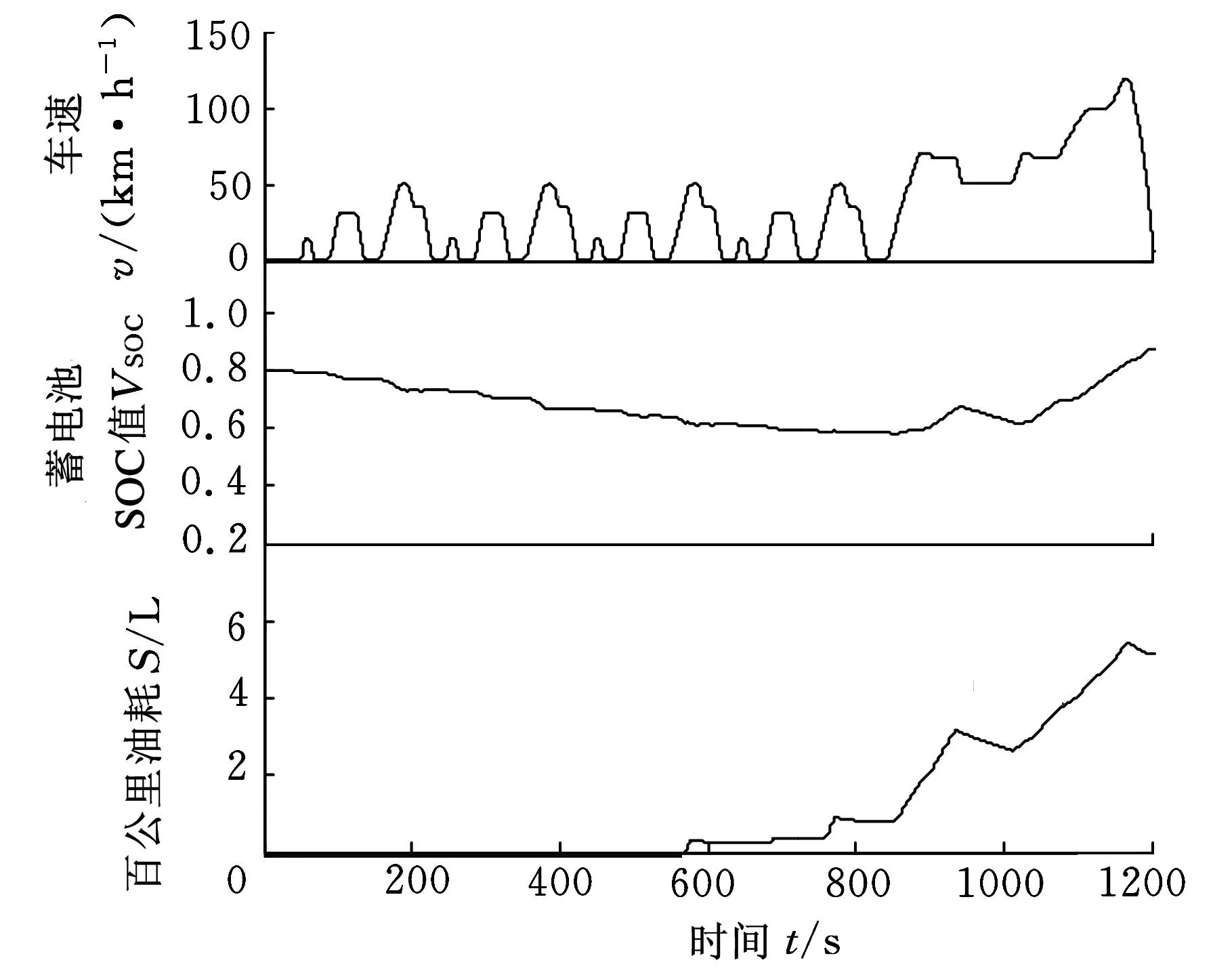
图16　燃油经济性仿真结果

4结论

(1)对功率分流系统机械点特性进行了分析，为使所提出的单模复合功率分流系统高效区间落在常用车速区间内，从使用拉维娜式行星齿轮结构的理论方案中筛选得出2种可行的结构布置方案。

(2)对前后行星排特征参数进行了优化，不仅从数学角度计算得出最优参数，而且从结构上推导得出该参数的限制条件。

(3)对系统工作模式进行了划分，包括纯电动模式、发动机启动模式、混合驱动模式和制动模式。利用杠杆法对各种工作模式的原理进行了分析。

(4)对该混动系统进行油耗仿真，在NEDC循环工况下等效燃油消耗量仅为4.68L/100km。

参考文献:

[1]项昌乐,韩立金,刘辉,等.混联混合动力车辆功率分流耦合机构特性分析[J].汽车工程,2010,32(3):183-187.

Xiang Changle,Han Lijin,Liu Hui,et al.An Analysis on the Characteristics of Power-split and Coupling Mechanism in Series/Parallel HEV[J].Automotive Engineering,2010,32(3):183-187.

[2]Wishart J,Yu L,Zhou L,et al.Review of Multi-regime Hybrid Vehicle Power Train Architecture[J].International Journal of Electric and Hybrid Vehicles,2008,3(1):248-275.

[3]Gupta A K,Ramanarayanan C P.Analysis of Circulating Power within Hybrid Electric Vehicle Transmissions[J].Mechanism and Machine Theory,2013,64(1):131-143.

[4]Grewe T,Conlon B,Holmes A.Defining the General Motors 2-Mode Hybrid Transmission[J]//SAE Technical Paper 2007-01-0273,2007.

[5]张彤,余为,马智涛,等.一种双行星排四轴传动装置:中国,102022489 A[P].2011.

[6]冯樱.运用杠杆法计算汽车行星齿轮变速器的传动[J].湖北汽车工业学院学报,2008,22(3):17-20.

Feng Ying.Analysis on the Ratios of AT by Lever Method[J].Journal of Hubei Automotive Industries Institute,2008,22(3):17-20.

[7]Schulz M.Circulating Mechanical Power in a Power-split Hybrid Electric Vehicle Transmission[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2004,218(6):1419-1425.

[8]步曦,杜爱民,薛锋.混合动力汽车用行星齿轮机构的理论研究与仿真分析[J].汽车工程,2006,28(9):834.

Bu Xi,Du Aimin,Xue Feng.Theoretical Study and Simulation on Planetary Gear Set for Hybrid Electric Vehicle[J].Automotive Engineering,2006,28(9):834.

[9]Yang H,Cho S,Kim N.Analysis of Planetary Gear Hybrid Power Train System Part 1:Input Split System[J].International Journal of Automotive Technology,2007,8(6):771-780.

(编辑苏卫国)