近空间飞行器多模态切换控制研究

顾臣风，江驹，甄子洋，吴雨珊

(南京航空航天大学 自动化学院，江苏 南京210016)

0 引言

近空间飞行器通常工作在距地面20～100 km的临近空间范围，以高于Ma=5的速度高速飞行，具有激烈快时变、严重非线性、强耦合和不确定性四大特点。近空间飞行器工作的临近空间大气密度和空气压力变化剧烈，因此飞行器的气动特性会受到较大影响。在给定的飞行高度和速度飞行时，由于大气密度和气动力的变化，舵面偏转相同的角度将会产生不同的力矩。

在飞行器的飞行过程中，飞行器的速度会产生大范围快变，而马赫数的剧烈变化将导致飞行器的气动特性和飞行力学特性的激烈变化。而传统的控制器设计方法在针对飞行器大包络飞行时，采用巡航飞行时的平衡点线性化模型进行设计，其设计的控制器随着飞行状态的改变系统状态会偏离原先的平衡点，这会导致控制效果的下降甚至使得整个系统发散［1］。针对大范围指令跟踪时产生的问题，国内外的研究者进行了一系列研究［2-6］。本文针对近空间飞行器的大包络飞行，研究基于速度的多控制律切换策略，实现飞行器的大范围速度指令跟踪。近空间飞行器在执行不同的飞行任务时，需要进行飞行模态的切换，针对近空间飞行器在巡航段飞行过程中存在的模态转换问题，研究了模态切换控制方法，可保证模态切换的有效性、平稳性和快速性。

1 近空间飞行器动力学模型

本文采用在“椭球地球”条件下建立的飞行器模型。在近空间飞行器滚转角和侧滑角满足θ=β≡0的条件下，得到飞行器的纵向运动方程［7］如下:

2 反步控制器设计

近空间飞行器的纵向模型是一个多输入多输出的非线性耦合系统，因此，对飞行器的速度和高度利用精确反馈线性化得到近空间飞行器输入输出线性化模型:

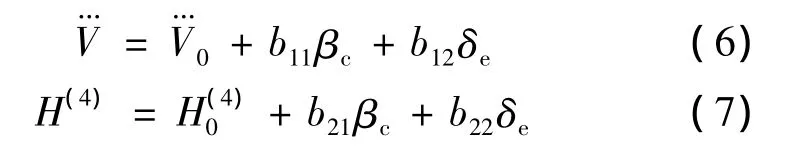
定义坐标变换

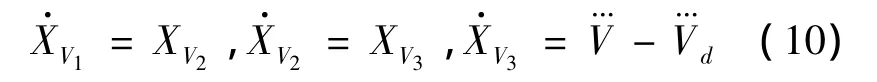
第一步:对于系统(10)的第一个子系统，定义ZV1=XV1，定义XV2虚拟控制为:

式中:φV1(·)为设计的K类函数;设计常数CV1＞0。定义误差变量，则

第二步:对于ZV1和ZV2，定义李雅普诺夫函数，由第一步可知，可得:

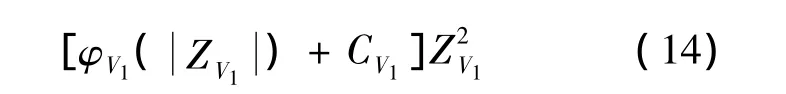
定义XV3虚拟控制为:

式中:φV2(·)为设计的K类函数;设计常数CV2＞0。定义误差变量，则

由式(14)可得:

第三步:对于 ZV1，ZV2，ZV3，定义李雅普诺夫函数，由第二步可知，令，则，可得:

则速度误差跟踪系统的控制输入:

式中:φV3(·)为设计的K类函数;设计常数CV3＞0。

因此，速度误差跟踪系统在控制输入的作用下渐近稳定。

整理得:

3 基于速度的多控制律切换控制

3.1 局部平衡点集的建立及切换机制设计

考虑高超声速飞行器纵向通道的系统模型，假设系统的输出空间为Y，在Y中选取N个输出y0≤y1≤…≤yN－1，并得到相应的平衡点(xi，ui，yi)，i=0，1，…，N－1。表1为高超声速飞行器不同高度及速度下的配平点。

表1 配平点Table 1 Trim point

基于速度的多控制律切换算法［8］如下:

3.2 基于速度的多控制律切换控制仿真

飞行器初始状态在V=4 590.3 m/s，H=33 528 m，指令信号 V=4 770.3 m/s，H=33 828 m。在初始状态和指令信号间选取两个平衡点V=4 650.3 m/s及V=4 710.3 m/s，针对初始状态以及两个平衡点分别设计各平衡点对应的控制律［9］，控制律1，2，3的输出分别为 uA，uB，uC。仿真系统结构、飞行器的速度和高度响应、飞行状态变化如图1～图3所示。

图1 切换控制系统结构图Fig.1 The structure of switching control system

图2 飞行速度和高度响应曲线Fig.2 Simulation results of flight speed and altitude

图3 航迹角、迎角和俯仰角速率变化曲线Fig.3 Simulation results of angle of flight path，angle of attack and pitch rate

可以看出:基于速度的多控制律切换策略的闭环状态响应最终都稳定在指令值;在仿真过程中，航迹角、迎角和俯仰角速率均在合理范围内变化。系统进行了两次切换，分别在V=4 650.3 m/s和V=4 710.3 m/s处，每个阶段的实际输出都能很好地跟踪各自的指令信号，证明了切换控制策略的有效性和平稳性。

4 巡航段模态切换控制

假设飞行器先从爬升加速模态进入空速保持模态，最后切换到平飞加速模态。模态切换的关键问题在于切换时机的选取，本文采用两种方法:一种是基于时间的切换，在时间点20 s和40 s处进行模态的切换;另一种通过判断速度和高度是否到达给定值来进行模态的切换。

基于特定时间的切换算法为:

基于速度和高度的切换算法为:

基于特定时间点的切换控制算法，飞行器的速度和高度响应以及控制输入变化曲线如图4和图5所示。

图4 飞行器速度和高度响应曲线Fig.4 Simulation results of flight speed and altitude

图5 控制输入变化曲线Fig.5 Simulation results of control input

由图可知，飞行器对指令信号具有较快的响应速度以及精确的跟踪性能。20 s时飞行器从爬升加速模态变化到空速保持模态，控制输入油门开度变化很小，只有舵面激烈变化，这是因为高度的变化主要依赖于舵面。40 s时飞行器从空速保持模态切换到平飞加速模态，此时舵面变化很小，油门开度变化较大，这是由于平飞加速模态的高度保持恒定，而速度的增加主要依赖油门开度的增大。

第二种切换方式是基于速度和高度的切换控制，飞行器的速度和高度响应以及部分飞行状态变化曲线如图6和图7所示。

图6 飞行器速度和高度响应曲线Fig.6 Simulation results of flight speed and altitude

图7 航迹角、迎角和俯仰角速率变化曲线Fig.7 Simulation results of angle of flight path，angle of attack and pitch rate

由仿真结果可知，基于时间的切换在切换时速度和高度值都已经处于稳态一段时间，而第二种切换方式在速度和高度都达到设定值时才进行切换。两种切换控制都很好地达到了控制要求，航迹角、迎角、俯仰角速率以及控制输入都在合理范围内变化。

5 结束语

首先，本文针对近空间飞行器的速度和高度误差跟踪系统进行反步控制器设计。其次，针对飞行器在巡航段大包络飞行时传统的控制器设计方法的不足，采用了多控制律切换控制策略实现飞行器大范围的指令跟踪。仿真验证表明，切换控制策略能高效快速跟踪指令信号，且不存在稳态误差，具有良好的控制效果。最后，针对巡航段的三个模态进行多模态切换控制研究，仿真结果表明，本文设计的多模态切换控制策略具有良好的控制效果。

［1］ 严玲玲.基于高超飞行器柔性模型的预测控制与动态仿真［D］.上海:上海交通大学，2012.

［2］ 罗建军，常江，王章磊，等.一种再入飞行器鲁棒控制器软切换方法［J］.飞行力学，2014，32(4):329-333.

［3］ Rehman O U，Petersen I R，Fidan B.Feedback linearization-based robust nonlinear control design for hypersonic flight vehicles ［J］.Systems and Control Engineering，2012，227(1):3-11.

［4］ Xu Bin，Pan Yongping，Wang Danwei，et al.Discrete-time hypersonic flight control based on extreme learning machine［J］.Neurocomputing，2014(128):232-241.

［5］ Kuipers M，Ioannou P，Fidan B.Robust adaptive multiple model controller design for an airbreathing hypersonic vehicle model［R］.AIAA-2008-7142，2008.

［6］ Li Hongyi，Wu Ligang，Gao Huijun，et al.Reference output tracking control for a flexible air-breathing hypersonic vehicle via output feedback［J］.Optimal Control Applications and Methods，2012，33(4):461-487.

［7］ 刘燕斌.高超声速飞行器建模及其先进飞行控制机理的研究［D］.南京:南京航空航天大学，2007.

［8］ 席裕庚，王凡.非线性系统预测控制的多模型方法［J］.自动化学报，1996，22(4):456-461.

［9］ 朱艳明.高超声速飞行器的非线性控制［D］.沈阳:东北大学，2009.