连分式的逼近计算及其Mathematica实现
李声锋 陈栋栋
(蚌埠学院应用数学研究所,安徽 蚌埠 233030)
在数值计算中,由于多项式具有任意阶可导、易于求积等特点,在很多情况下采用多项式逼近函数,如Taylor级数展开法、Maclaurin级数展开法等。但有时遇到函数在某点无界等情形,此时解决此类问题需要用到有理逼近。连分式是一个经典的有理逼近工具,是研究非线性问题的首选方法,应用广泛。
Mathematica软件是一款功能强大的符号计算语言,广泛应用在数学领域。在数学研究和教学过程中,利用Mathematica软件平台可以实现各种计算和仿真。我们在利用连分式逼近函数的近似计算过程中,借助于Mathematica软件,编写了程序,快速实现了连分式的逼近计算,并将计算结果与多项式级数逼近结果进行了比较。
1 预备知识
定义1 设2个复数列{an}和{bn},称形如
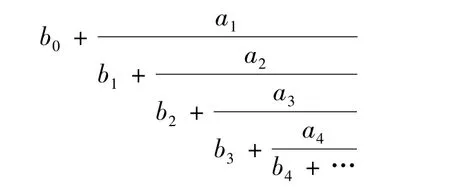
的分式为连分式(Continued fractions),记作
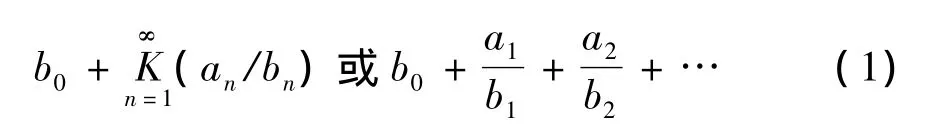
2 连分式逼近函数
2.1 连分式逼近函数

式(2)前几项的渐近分式分别为
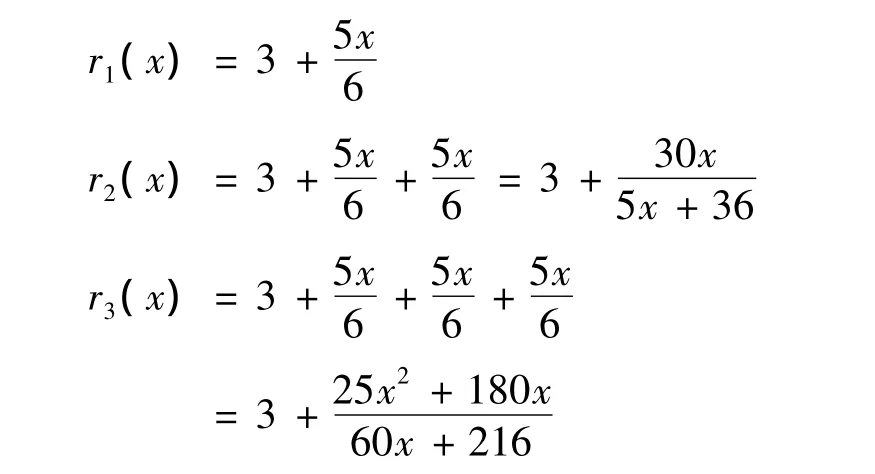
2.2 逼近计算结果的Mathematica实现
为了直观显示连分式(2)的渐近分式逼近计算结果,下面分别取 x=0.65,x=8,进行逼近计算,并编写Mathematica程序:
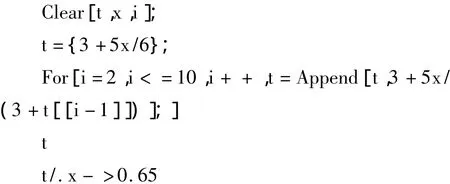
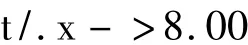
运行程序,我们不仅能看到给出的渐近连分式,还得到渐近分式的计算结果。当x=0.65时,利用式(2)的四次渐近分式就能计算得到函数值f(0.65)=3.50;当 x=8.00 时,利用式(2)的十次渐近分式就能计算得到函数值f(8.00)≈7.00。具体计算结果见表1。

表1 式(2)渐近式在x=0.65与x=8.0时的函数值(取前10项)
2.3 连分式逼近与多项式逼近的比较
从表1可以看到,连分式在数值近似计算中能得到较好的逼近结果,下面考虑函数 f(x)=的多项式逼近,并与连分式逼近进行比较。我们将函数作如下的Maclaurin级数展开

其中
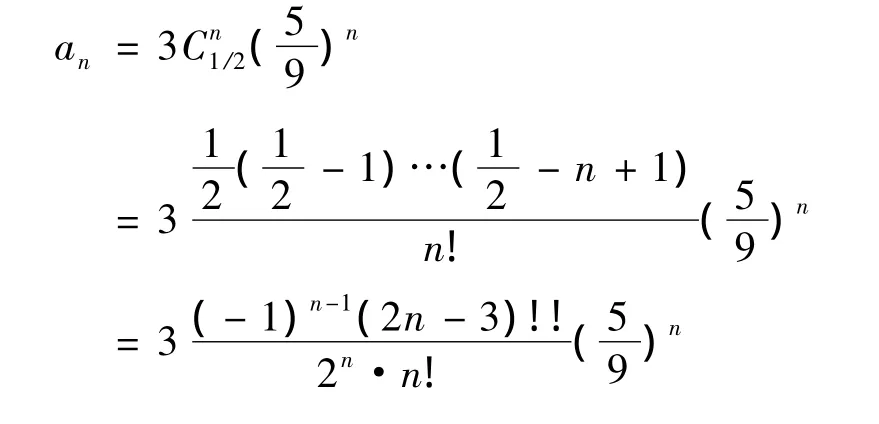
利用Mathematica软件计算Maclaurin展开式(3)在x=0.65与x=8.00时的近似结果,编写程序如下:
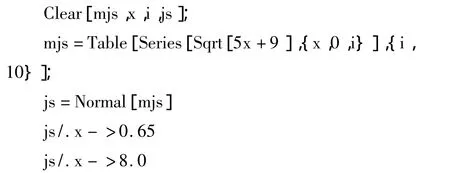
运行上面的程序,我们可以看到Maclaurin展开式的部分和,还得到了部分和的计算结果。当x=0.65时,利用式(3)的前6项之和就能计算得到函数值 f(0.65)=3.50;当 x=8.00 时,此时级数发散,无法利用式(3)的部分和得到函数值,具体计算结果见表2。

表2 式(3)的部分和在x=0.65与x=8.00的函数值(取前十项)
从表1和表2的计算结果,我们可以看到如下事实:
3 结语
本文通过实例讨论了连分式逼近的近似计算问题,利用Mathematica软件编写程序,快速实现了连分式的逼近计算,并将计算结果与多项式级数逼近结果进行了比较。比较结果表明,连分式逼近函数比多项式级数逼近函数不仅速度较快,而且具有较大的收敛区域。在某种意义上说,连分式逼近是一种行之有效的逼近方法,在近似计算中可以获得较优的计算结果。
[1]檀结庆.连分式理论及其应用[M].北京:科学出版社,2007.
[2]王仁宏,朱功勤.有理函数逼近及其应用[M].北京:科学出版社,2004.
[3]李声锋,董毅.大学数学实验[M].上海:上海交通大学出版社,2015:40-50.
[4]Lorentzen L,Waadeland H.Continued Fractions with Applications[M].North-Holland:[s.n.]1992.
[5]Tan J Q,Zhao Q J.Successive Newton-Thiele's rational interpolation[J].J.Inform.Comput.Science,2005,15(2):74-83.
[6]Tan J Q.The Limiting Case of Thiele's Interpolating Continued Fraction Expansion[J].J.Comput.Math.,2001,19(4):433-444.
[7]林成森.数值计算方法[M].北京:科学出版社,2001:30-50.
[8]刘玉琏,傅沛仁.数学分析讲义:下册[M].第5版.北京:高等教育出版社,2013:30-55.

