导向钻井稳定平台广义预测控制的Matlab/GUI设计

霍爱清 周金慧 汪跃龙

(西安石油大学陕西省钻机控制技术重点实验室，西安 710065)

稳定平台是调制式旋转导向钻井工具的重要机构，可以沿轴自由转动。它可使施加到平台上的力矩保持平衡，并调整控制轴的工具面角，使井下钻井工具在旋转的同时能够完成导向造斜，最终控制井眼轨迹［1-3］。在实际钻井过程中，受井下工作环境、地层结构及钻压等因素的影响，稳定平台模型参数会存在不确定性，从而使系统的动态特性复杂化，因此难以保证稳定平台控制指标。在线性控制系统设计中常用的分析和设计方法具有一定的局限性，传统的控制方法难以满足要求，系统控制效果不理想。

将广义预测控制算法(GPC，即generalized predictive control)应用到旋转导向钻井稳定平台是一种新的方法。该算法采取多步预测、滚动优化和反馈校正策略，具有良好的控制效果和较强的鲁棒性，对模型精确度要求低，适用于不易建立精确数学模型的复杂工业过程［4］。Matlab中的GUI(graphical user interfaces)开发环境提供了创建用户界面的捷径。本次研究中，利用GUI的这一特性设计广义预测控制仿真平台，对稳定平台进行仿真分析。

1 稳定平台模型的建立

导向钻井稳定平台系统实质上是一个闭环负反馈的位置控制系统。系统根据角位置给定的指令开始工作，当没有新指令到来时按照定值系统工作，自动克服闭环内的各种干扰，使导向工具指向固定的工具面角。当接到新的指令后，稳定平台按照位置随动系统原理开始工作，随后导向工具旋转并指向给定角度。旋转导向钻井在进行导向造斜时，稳定平台会处于稳定调节状态，此时系统出现较强的摩擦现象。稳定平台工作于井下，工作环境复杂多变，上、下盘阀间的压强随井下工况不断变化，盘阀间的摩擦力矩也会周期性变化［5］。

稳定平台控制系统为闭环反馈系统，系统工作原理框图如图1所示，整个被控对象的结构框图如图2所示。图中各系数的关系为:

其中:f—黏性摩擦系数;

Ra— 电枢电阻，Ω;

Ce—反电动势系数;

Cm—电机转矩系数;

J—稳定平台转动惯量，kg·m2;

Km—电机传动系数;

Tm—电机机电常数。

若仅考虑稳定平台被控对象，可得式(1):

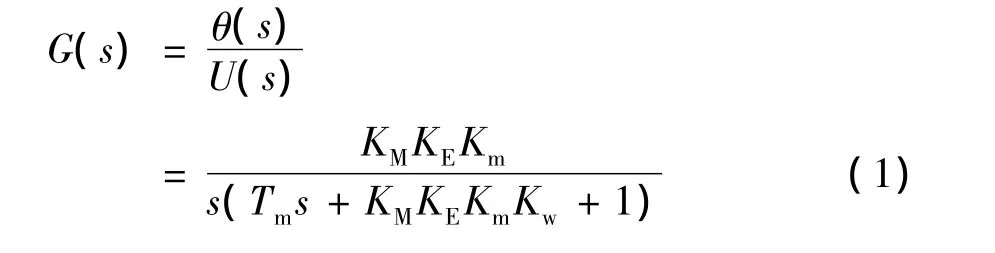
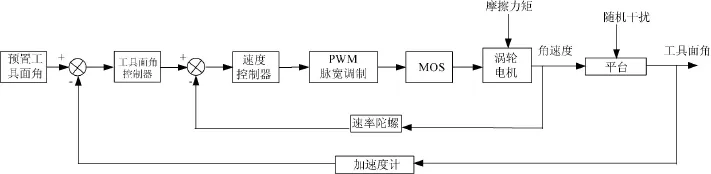
图1 稳定平台闭环控制系统原理框图

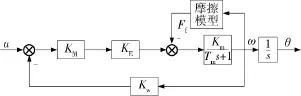
图2 稳定平台被控对象结构框图

式中:KM—PWM脉宽调制系数，A/V;

KE—电枢电流与电磁力矩之比例常数;

Kw—陀螺传感器转换系数，V·s/rad;

Ff—摩擦力矩;

G(s)—控制对象传递函数;

θ(s)—输出函数;

U(s)—输入函数。

经过多次地面试验及井下试验，该系统模型的有效性已被验证［6］。

根据实验测得的稳定平台控制对象特征及机械设计数据，得到平台的模型参数KM=3.440(A/V);KE=0.220;Kw=5.740(V·s/rad);J=0.030(kg·m2)，f=0.270，Ra=12.500(Ω)，Ce=0.400，Cm=3.820。带入式(1)可得控制对象传递函数为:

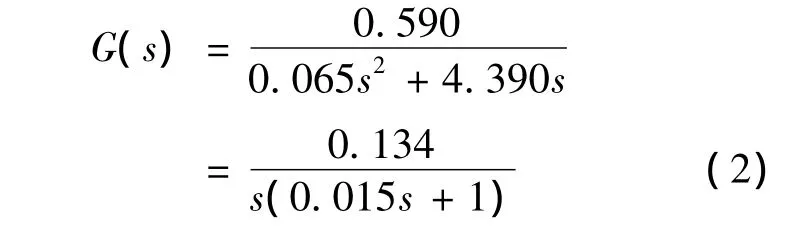
对其进行离散化，可得式(3):

2 广义预测控制算法

广义预测控制以受控自回归积分滑动平均模型(CARIMA)为基础，具有滚动优化的优点，是鲁棒性较强的一种控制算法［7-8］。

在实际应用过程中，经常会遇到扰动的问题;而CARIMA模型由于引入了积分，可以自动消除非零设定值引起的误差，保证系统的稳定误差为零，对非平稳随机噪声过程有一定的适用性。被控对象的CARIMA模型可以如式(4)所示:

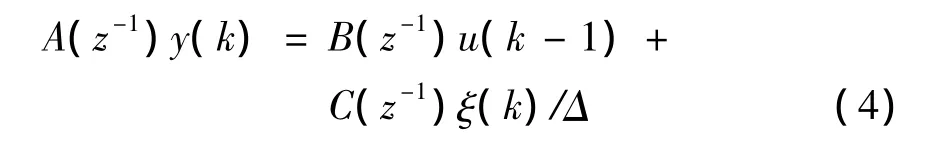
式中，y(k)、u(k)、ξ(k)分别为系统的输出量、输入量和白噪声序列，Δ=1-z-1为差分算子，且

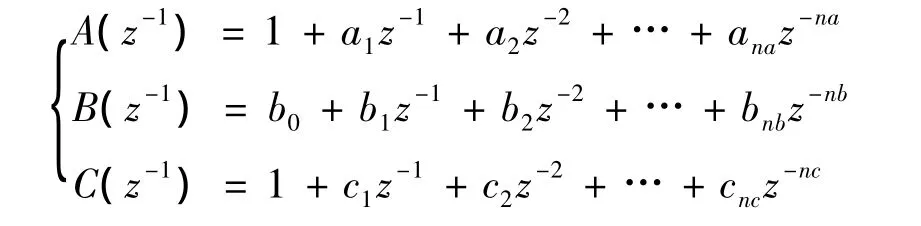
如果需要增强系统的鲁棒性，应考虑当前时刻的控制对下一时刻的影响，采用目标函数P:

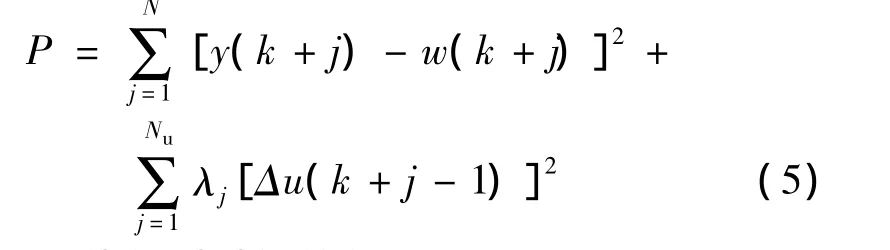
其中:N—优化时域的终值;

Nu—控制时域;

λj— 控制权系数;

w(k+j)—参考轨迹。

为了进行柔化控制，使输出直接跟踪参考轨迹，则参考轨迹由式(6)产生:

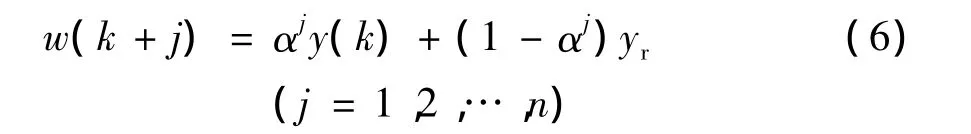
式中，yr为设定值，y(k)为输出值，α为柔化系数。

目标函数最后一项的作用主要是为了使控制增量变化不会过于激烈，避免发生剧烈震荡。因此，广义预测控制问题最终归于求解 Δu(k)，△u(k+1)，…，Δu(k+Nu-1)，从而得到目标函数最小值。

为了预测超前j步输出数据，引入Diophantine方程:

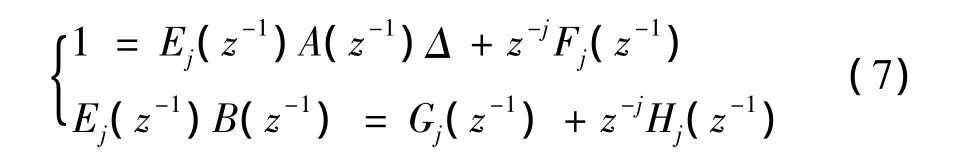
其中:

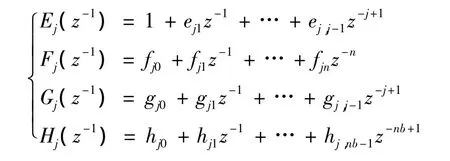
综合以上各式，可以得到:

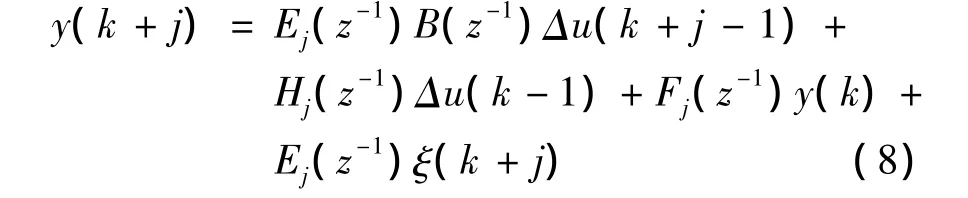
而对于未来输出的预报，若忽略未来噪声的影响，可以得到输出估计值:

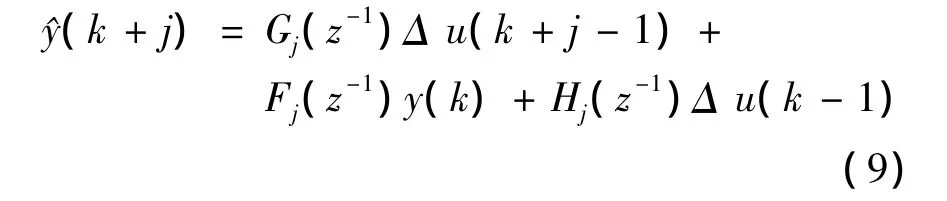
式(9)中包含2部分，用f(k+j)表示已知量，写成矩阵形式:

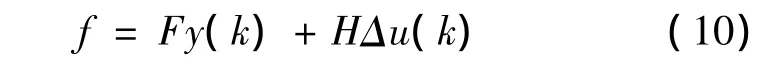
其中

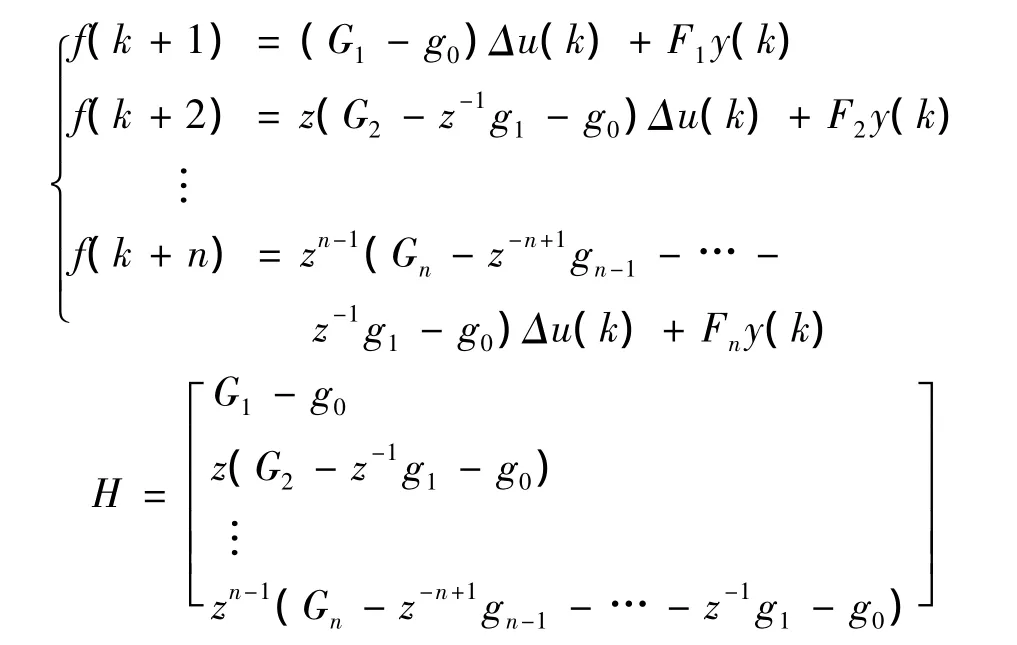
整理可得最优输出预测值为:

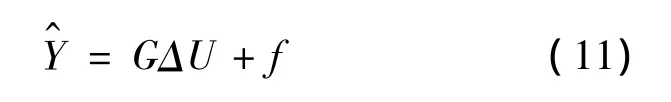
其中

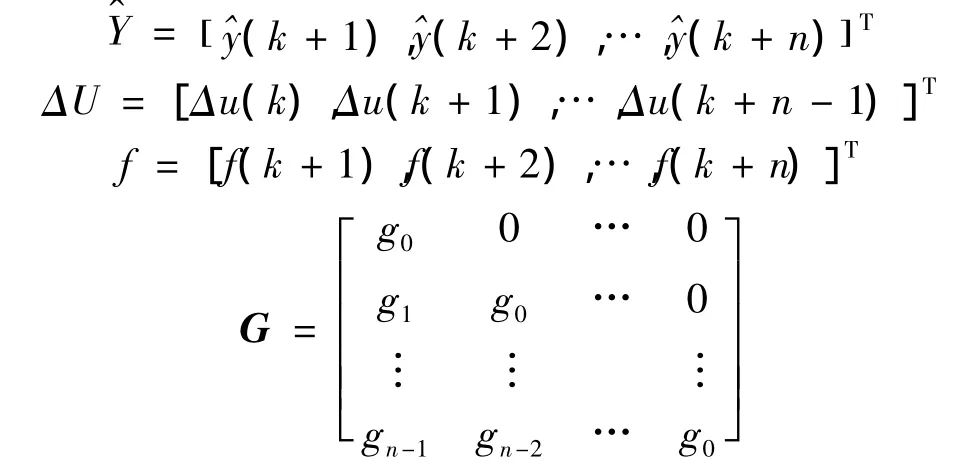
将式(11)带入式(5)，整理可得目标函数:

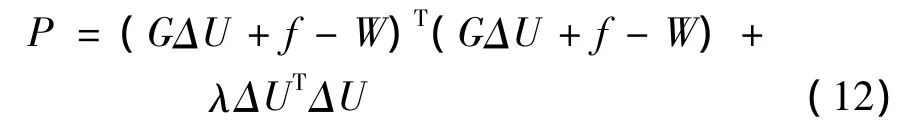
令P/ΔU=0，得到控制增量的向量为:

这样就可以得到即时最优控制量为:

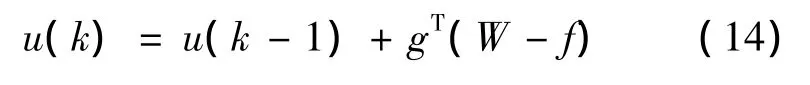
式中，gT为(GTG+λI)-1GT的第一行。

3 基于MATLAB仿真平台的设计

利用MATLAB的图形用户界面(GUI)，进行导向钻井稳定平台广义预测控制人机交互界面的设计［9］。利用 MATLAB的 GUIDE创建图形用户界面，GUI对于每个用户窗口会生成一个“.fig”文件(负责界面的设计信息)和一个“.m”文件(负责后台代码的设计)。

3.1 利用GUIDE进行界面设计

GUIDE能够很好地帮助我们完成界面的设计和布置工作，界面的设计要求制作的界面应简洁，布局合理而又比较直观、易于操作。

界面主要包括输入/输出模块、算法模块和仿真模块。输入模块主要完成对象模型及系统参数的输入;算法模块主要是完成广义预测控制算法的实现;仿真模块是对实际对象的模拟，根据算法模块给出的控制输入仿真计算出系统输出。用户界面控件主要响应用户的鼠标动作，然后通过编写回调函数，对界面控件的callback属性编辑实现GUI的基本机制。

利用GUIDE设计仿真平台界面，如图3所示。

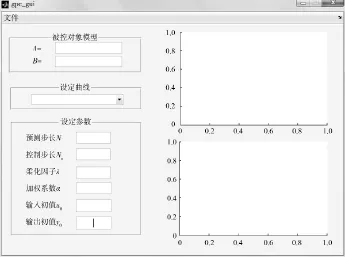
图3 仿真平台界面

3.2 仿真结果分析

由式(3)转换得到CARIMA模型:

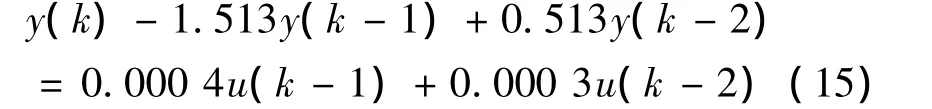
3.2.1 阶跃输入时工具面角跟踪响应

在界面中设置旋转导向钻井稳定平台被控对象的模型参数，将设定曲线定为阶跃信号，点击文件里的运行按钮，进行仿真。通过调节控制参数，得到稳定的工具面的响应曲线和误差曲线，如图4所示。由曲线可以看出，系统可以在较短的时间达到稳定状态，并且对稳定状态的跟踪精度较高。

3.2.2 鲁棒性

(1)研究盘阀摩擦对系统的影响。旋转导向钻井稳定平台工作于井下，井下工况复杂多变，上下盘阀间的压强也随着不断变化，盘阀间的摩擦力矩呈现周期性特征。在算法模块加入摩擦扰动，将设定曲线设置为正弦曲线，对系统进行仿真。摩擦扰动时工具面角跟踪曲线如图5所示。可以看出系统拟合度高，具有良好的跟踪特性和较强的鲁棒性。

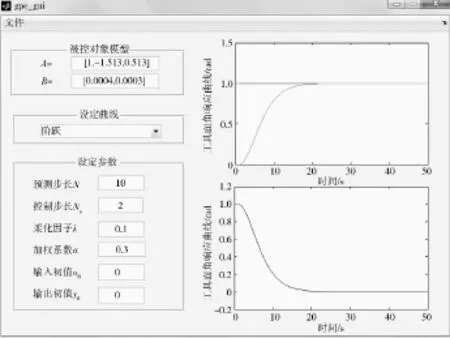
图4 工具面角响应曲线

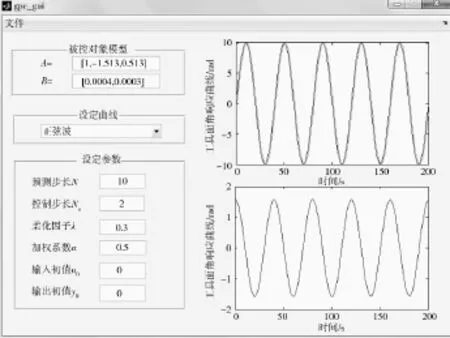
图5 考虑摩擦扰动时工具面角跟踪曲线

(2)参数摄动对系统的影响。稳定平台在井下受泥浆、温度等的影响，稳定平台转动惯量J和负载电阻Ra均会受到影响。当J和Ra均减小50%时，控制对象的传递函数变为:

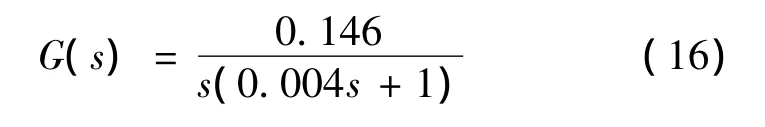
转换成CARIMA模型:

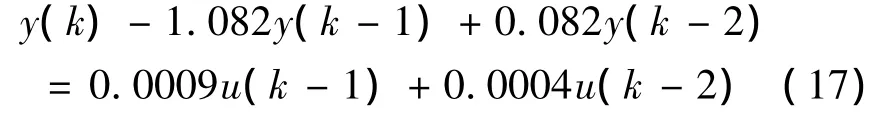
通过仿真，得到图6所示的工具面角跟踪曲线。广义预测控制算法在模型失配的情况下依然可以达到较为理想的控制及跟踪性能，系统鲁棒性好，并能克服外干扰及摩擦特性对系统的影响。

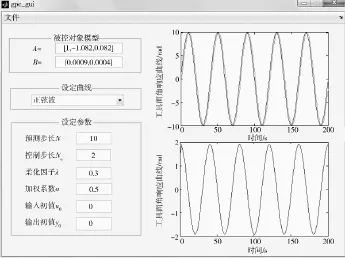
图6 J和Ra减小50%时工具面角跟踪曲线

4 结语

根据井下导向钻井工具的实际工作情况，建立带有摩擦扰动的稳定平台广义被控对象数学模型。针对稳定平台存在的摩擦问题，利用 Matlab的GUIDE工具设计了广义预测控制仿真平台，以交互的方式实现了对导向钻井稳定平台系统的仿真研究。仿真结果表明广义预测控制器能够有效抑制摩擦，具有较好的鲁棒性，并显示出良好的动态性能和稳态精度，使控制性能得到极大改善。

［1］霍爱清，贺昱曜，汤楠，等.旋转导向钻井工具稳定平台模糊滑模控制研究［J］.计算机仿真，2010，27(10):152-155.

［2］汤楠，霍爱清，汪跃龙，等.旋转导向钻井工具稳定平台控制功能试验研究［J］.石油学报，2008，29(2):284-287.

［3］汤楠，穆向阳.调制式旋转导向钻井工具稳定平台控制机构研究［J］.石油学报，2003，25(2):9-12.

［4］Ramasamy M，Narayanan S S，Rao C D.Control of Ball Mill Grinding Circuit Using Model Predictive Control Scheme［J］.Journal of Process Control，2005，15(3):273-283.

［5］汪跃龙，张璐，汤楠，等.旋转导向钻井惯导平台动力学分析与运动研究［J］.机械工程学报，2012，48(17):65-69.

［6］霍爱清.旋转导向钻井稳定平台系统模型辨识及控制方法研究［D］.西安:西北工业大学，2012:35-37.

［7］Clarke D W，Mohtadi C，Tuffs P S.Generalized Predictive control—Part I:the Basic Algorithm ［J］.Automatica，1987，23(2):137-148.

［8］李国勇.智能控制及其MATLAB实现［M］.北京:电子工业出版社，2005:1258-259.

［9］王玉林，葛蕾，李艳斌.新型界面开发工具:MATLAB/GUI［J］.无线电通信技术，2008，34(6):50-52.