小波变换和EEMD-马氏距离的轴承故障诊断

艾延廷，冯研研，周海仑

（沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136）

小波变换和EEMD-马氏距离的轴承故障诊断

艾延廷，冯研研，周海仑

（沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136）

机械故障的声发射信号中往往掺杂着各种干扰和噪声，为解决这一问题，提出了小波变换、集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）和马氏距离相结合的滚动轴承故障诊断方法；首次将马氏距离引入到轴承声发射信号的故障诊断中。该方法首先对故障轴承的声发射信号进行小波去噪处理，再对去噪后的信号进行EEMD分解，将其分解为多个固有模式函数（简称IMF）。其次采用马氏距离的方法消除EEMD分解结果中的虚假分量，提取能够反映轴承故障特征的IMF分量，突出高频共振成分。最后，通过瞬时Teager能量的Fourier频谱识别轴承故障的特征频率。仿真信号和滚动轴承外圈声发射信号的实例分析表明：此方法能很好地去除混杂在轴承声发射信号中的噪声，准确地识别出轴承故障的部位。

振动与波；故障诊断；小波变换；集合经验模态分解；Teager能量谱分析

滚动轴承是旋转机械中最易损坏的关键零部件之一，对其进行状态监测和故障诊断有着广泛的经济和社会效益。近年来，用声发射方法检测机械故障已经得到了广泛应用，传统的线性滤波方法去噪效果并不理想，小波方法已广泛应用于声发射信号去噪和特征提取领域[1]。小波分析具有良好的时频局域性，特别适合于非平稳信号的分析，但是小波去噪效果也与信号的特点及小波基函数和分解层次的选取有关。经验模态分解（EMD）方法是由Huang[2]提出的，它能够对非线性、非平稳的信号进行线性化和平稳化处理。但是EMD方法处理复杂的非线性非平稳信号时，由于信号中含有间断事件，导致其在频率上的尺度缺失，出现模态混叠现象，集合经验模式分解(EEMD)就是针对EMD这一缺陷提出来的[3]。马氏距离是一种能够计算两个未知样本集相似度的方法，目前马氏距离主要应用在电路故障诊断中[4，5]，本文首次将马氏距离引入到滚动轴承故障诊断中，取得了良好的效果。

将小波变换和EEMD分解法相结合对滚动轴承的声发射信号进行特征提取，通过马氏距离选取能够反映故障特征的IMF分量，并通过Teager能量谱分析提取轴承故障频率，通过仿真信号和滚动轴承声发射实验验证了本文提出的方法有效性。

1 小波降噪原理

小波变换具有时域和频域的良好局部特性，一般地，噪声信号包含在较高频率的细节中，而有用的信号则表现为低频信号，因此可利用门限阈值对小波分解后的小波系数进行处理。小波阈值去噪理论最早是由Donoho[7]提出的。小波阈值去噪算法主要分为4个步骤：

第一步：选择合适的小波基和小波分解层数，对信号进行小波分解，分解层数一般为3—5层[8]；

第二步：选择合适的阈值函数；

常用的阈值函数有以下两种：

[软阈值函数]

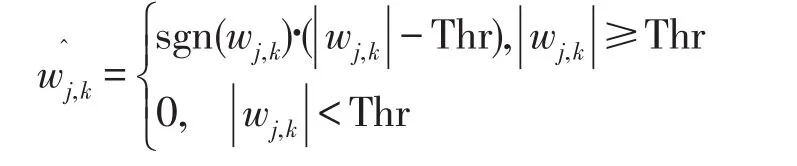
[硬阈值函数]

第三步：选择合适的阈值。

阈值的选择在小波降噪的过程中起决定性作用，当小波分解后的小波系数小于选定的阈值时，认为小波系数主要是由于噪声引起的，应该置为零；当小波系数大于选定的阈值时认为小波系数主要是由于信号引起的。常用的阈值选择方案有：无偏似然估计的软阈值估计、通用阈值、启发式阈值、最小极大方差阈值。

第四步：小波重构。

2 EEMD-马氏距离基本原理

2.1 EMD原理

EMD方法对信号进行分解后得到多个IMF，这些IMF必须满足两个条件：一是其极值点个数和过零点个数相同或最多相差一个；二是其上下包络线关于时间轴局部对称。

EMD原理如下[9，10]：

1）寻找信号x(t)的所有极大值和极小值，然后采用三次样条插值算法分别获得信号的上包络线xh(t)和下包络线xL(t)，同时计算出两条包络的平均值m(t)为

2）设变量x1(t)为

若x1(t)满足IMF的两个标准则，可以作为第一个IMF，并记为c1(t)否则作为原始信号重复1）和2），直到得到第一个IMF分量。

3）计算剩余信号

把其作为新的信号重复1）和2）直到提取完所有IMF分量。当剩余的信号为非振荡的单调函数或小于预定值的数，认为分解完毕。原始数据最终分解为n个IMF和一个剩余的向量rn(t)即

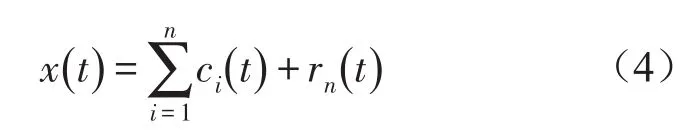
上述过程实际上是将原始信号x(t)分解成不同的IMF。

2.2 EEMD原理

Huang提出一种可以解决模态混叠问题的方法EEMD[11-12]，EEMD分解步骤如下：

（1）在原始信号上加一组随机正态分布的白噪声；

（2对加入白噪声后的信号进行经验模态分解，得到各个IMF分量；

（3）每次加入的随机正态分布白噪声的幅值是相同的，重复以上两个步骤，分解后得到各自的IMF分量组。Huang建议EMD分解次数为100时，白噪声的幅值取为原始信号标准差的0.1～0.5倍；

（4）取相应IMF的均值作为最终结果。

2.3 马氏距离

马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离[4]。它是一种有效的计算两个未知样本集相似度的方法。与欧氏距离相比,它不受量纲的影响,而且马氏距离能考虑到各种特性之间的联系,可以排除变量之间相关性的干扰。样本y和样本集m×n矩阵x之间的马氏距离定义为

m为样本向量的维数，n为样本的数量，x¯为矩阵x的重心，定义为

cx为矩阵x的协方差矩阵，定义为

3 Teager能量算子

对于任意信号x(t)，Teager能量算子ψ的定义为[13]

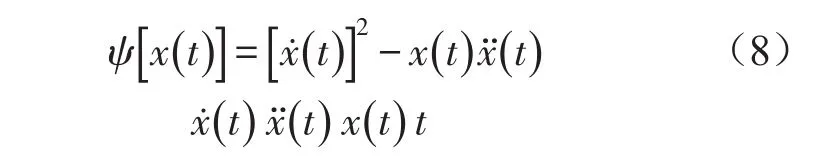
传统意义上的信号能量定义为信号幅值的平方，只代表动能或势能，Teager能量算子能够跟踪产生信号所需的总能量。故障轴承工作时会产生周期性冲击，周期性冲击的重复频率反映轴承的故障原因，根据这一原理，本文采用Teager能量谱对滚动轴承进行故障特征提取。

4 仿真信号分析

图1中可以看出仿真信号时域图中存在明显的冲击周期，且含有大量噪声，图2为仿真信号的频谱图，图中不能看出信号故障频率。经过多次试验，对仿真信号采用sym5小波基，使用软阈值函数，采用最小极大方差阈值法进行5层小波分解并重构，去噪后的如图3所示，去噪后的信号保留了原始信号的冲击周期，去除了大部分噪声。

图1 仿真信号时域图

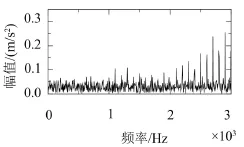
图2 仿真信号频谱图

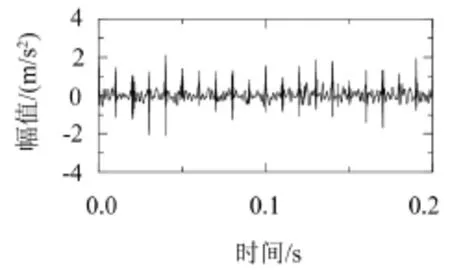
图3 仿真信号小波降噪后的时域图

对经过小波降噪后的信号进行EEMD分解，分解为6个IMF分量。分解后的图像如图4所示，

图4 EEMD分解图

图5为前五个IMF与原始信号的马氏距离，图中可见第一个IMF与原始信号马氏距离明显小于其它，故剔除后面的虚假分量，对第一个IMF进行后续的Teager能量谱分析。

图5 前五个IMF与原始信号的马氏距离

图6是IMF 1的Teager能量谱，图中可以看出100 Hz的特征频率，故障特征频率及其倍频成分十分明显，由此验证了基于小波变换和EEMD—马氏距离的信号特征提取的有效性。

5 滚动轴承声发射信号故障诊断实例

滚动轴承型号为TMB-N 204 M，采用线切割的方法在轴承的外圈上加工出宽0.5 mm，深0.5 mm轴向贯穿划痕。实验过程中，转速设置为计算得出滚动轴承外圈故障特征频率理论值：

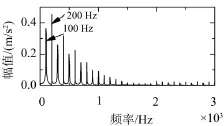
图6 去噪后的IMF1的Teager能量谱图

试验装置如图7所示，轴承基本参数如表2所示。

图7 轴承声发射信号故障检测试验台图尺寸对齐

表2 滚动轴承基本参数(mm)

图8为轴承声发射信号的时域图，图9为轴承声发射信号的频域图，图中均不能分辨出故障的特征频率，利用本文提出的方法对声发射信号进行故障特征提取。图10为经过小波降噪后的声发射信号的时域图，降噪后冲击特征更加明显。

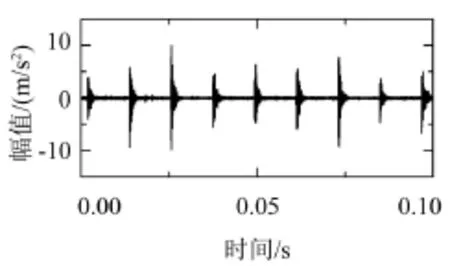
图8 轴承声发射信号的时域图

图9 轴承声发射信号的频域图

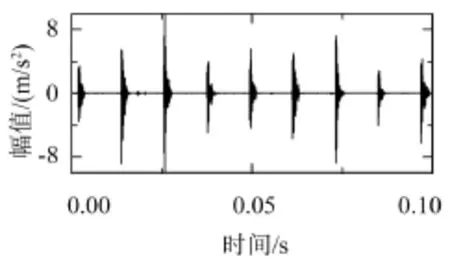
图10 轴承声发射信号小波降噪后时域图

采用EEMD的方法对小波降噪后的信号进行分解，前八个IMF分量如图11所示。

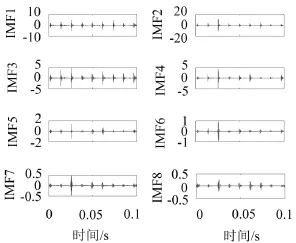
图11 EEMD分解结果IMF1-IMF8

图12为前五个IMF与原始信号的马氏距离，从图中可以看出第二个IMF分量与原始信号马氏距离最小，第一个IMF与原始信号的马氏距离次最小，因此剔除后面的虚假分量，对第一、二个IMF进行后续的Teager能量谱分析。

图13和图14是IMF1和IMF2的Teager能量谱图，图中可以明显看出83.92 Hz的特征频率，接近轴承外圈故障频率的理论值83.723 Hz，并且出现了高阶倍频，噪声干扰也得到有效抑，轴承故障特征明显直观。由于受到轴承参数和转速等误差干扰，计算出来的频率值与测得的真实值之间可能会有较小差异。综合以上分析，可以推断出轴承外圈发生了故障。通过滚动轴承声发射实验验证了本文提出的小波变换和EEMD-马氏距离的轴承故障诊断方法的有效性。

6 结语

(1)首次将马氏距离准则应用到轴承的声发射信号的特征提取中，提取EEMD分解后能反映原始信号故障特征的IMF分量，去除伪分量；

(2)将小波降噪与EEMD-马氏距离及Teager能量谱分析结合，应用到滚动轴承故障的声发射信号特征提取中，准确诊断滚动轴承的故障位置，该对推动轴承故障诊断和状态监测的发展有重要意义。

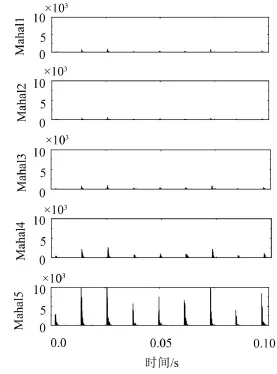
图12 前五个IMF与原始信号的马氏距离

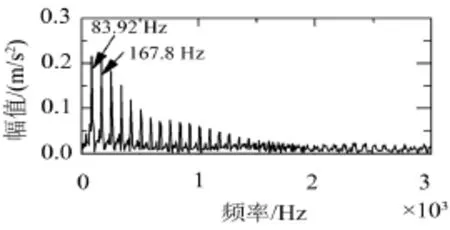
图13 去噪后的IMF 1的Teager能量谱

图14 去噪后的IMF2的Teager能量谱

[1]李孟源，尚振东，蔡海潮.声发射检测及信号处理[M].北京：科学出版社，2010.

[2]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc.R.Soc.Lond.A,1998,454:903-995.

[3]佟雨燕，陆森林.信号相关性和EEMD-Hilbert包络在滚动轴承故障诊断中的应用[J].噪声与振动控制，2013，33 (5)：144-147.

[4]秦庆强，张晓安，李艾华，等.马氏距离在模拟电路硬故障检测中的应用研究[J].电子测量与仪器学报，2009，23 (7)：41-45.

[5]赵建光，李红波，曾繁景，等.模拟电路的马氏距离故障诊断方法研究[J].电子测量技术，2012，35(3)：128-130.

[7]Donoho D L.De-noising by soft-threshold[J].IEEE Transaction on Information Theory,1995,41(3):613-627.

[8]臧怀刚，王志斌，郑英.改进小波阈值函数在局放去噪分析中的应用[J].自动化仪表，2010，31(5)：5-7.

[9]李志农，吕亚平，范涛，等.基于经验模态分解的机械故障欠定盲源分离方法[J].航空动力学报，2009，24(8)：1887-1889.

[10]Huang N E,Zheng S,Steven R.A new view of nonlinear water waves:The Hilbert spectrum[J].Annual Review of Fluid Mechanics,1999,31:417-457.

[11]Z H Wu,N E Huang.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances inAdaptive DataAnalysis,2009,1(1):1-41.

[12]夏均忠，苏涛，张阳，等.基于EEMD能量熵及LS-SVM滚动轴承故障诊断[J].噪声与振动控制,,2014，34(3)：171-172.

[13]王天金，冯志鹏，郝如江，等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击，2012，31(2)：2-3.

Fault Diagnosis of Roller Bearings Using Wavelet Transform and EEMD-Mahalanobis Distance

AI Yan-ting,FENG Yan-yan,ZHOU Hai-lun
(Liaoning key Laboratory ofAdvanced Measurement and Test Technology forAircraft Propulsion Systems,ShenyangAerospace University,Shenyang 110136,China)

The acoustic emission signal of mechanical faults is usually mixed with various kinds of interference and noise.In this article,a method of fault diagnosis of roller bearings was proposed using wavelet transform and EEMD-mahalanobis distance.First of all,the original acoustic emission signals were disposed by wavelet-denoising and decomposed into several stationary intrinsic mode functions(IMF)by EEMD.Then,the false IMFs of EEMD were eliminated by mahalanobis distance method so that the IMF components which could reflect the characteristics of bearing faults could be extracted. Finally,the Fourier spectrum of the transient Teager energy was used to recognize the characteristic frequencies of the bearing faults.Comparison of simulation signal with the measurement emission signal of the bearing with outer race faults show that the method can effectively remove the noise in the fault mixed signals,and identify the location of the bearing fault accurately.

vibration and wave;fault diagnosis;wavelet transform;ensemble empirical mode decomposition (EEMD);Teager energy spectrum analysis

TP206+.3

：A

：10.3969/j.issn.1006-1335.2015.01.048

1006-1355(2015)01-0235-05

2014－06－23

航空科学基金（2012ZB54007）；中航工业产学研专项(cxy2012sh17)

艾延廷，辽宁葫芦岛人，男，博士，主要研究方向为航空发动机结构强度、振动分析与故障诊断。

冯研研，女，硕士研究生。E-mail:693036922@qq.com