增量LTSA算法在转子故障数据集降维中的应用

胡常安，袁德强，王 彭，杜文波

（1.中国测试技术研究院，成都610021；2.兰州理工大学 机电工程学院，兰州730050）

增量LTSA算法在转子故障数据集降维中的应用

胡常安1，袁德强2，王 彭1，杜文波1

（1.中国测试技术研究院，成都610021；2.兰州理工大学 机电工程学院，兰州730050）

针对传统流形学习算法不具有增量学习能力；故难以处理新增数据与大规模海量数据集的问题，由此，提出一种用于机械转子故障数据集降维的增量局部切空间的排列算法(ILTSA)。该算法首先采用局部切空间排列算法对原始训练样本进行降维处理，获得其低维流形结构，然后通过增量学习算法对新增样本进行处理。得到所有数据的低维嵌入坐标，最后通过转子故障数据集验证了该方法的有效性，取得了良好的分类效果，有利于实时动态故障监测与诊断。

振动与波；故障诊断；人工智能理论；转子；局部切空间排列算法

流形学习作为一种非线性数据降维方法，能够发现高维非线性样本数据嵌入在高维数据空间中的低维流形结构。该算法对训练样本进行一次性学习而获得数据分类模型，新增数据时需对所有数据重新学习[1]。当需实时监测时数据不停的输送进来，重新学习导致对算法的要求极高。数据量十分庞大时，该算法只能采用分批处理的方法对数据进行处理。机械转子系统在运行过程中一旦发生故障，其振动数据表现出的非平稳、非线性特性将随着故障程度的加深而越加强烈。将流形学习用于高维非线性故障数据样本的学习，可有效发现其内在本质特征，便于故障的辨识与程度分析。万鹏等人[2]利用流形学习算法与支持向量机相结合，提高了机电系统故障诊断精度。杨庆等人[3]将流形学习算法用于轴承早期故障诊断，使得提取的故障特征敏感性更好，提高了模式识别能力。

但是，监测系统得到的信息嵌入在高维、大量的数据中，流形学习算法难以从高维数据流及大规模海量数据集中获得有价值的信息[4]，杨庆等人[5]提出了带标志点的增量流形学习算法，保证了轴承不同状态样本间较高的类别可分性。朱明旱等人[6]提出了基于正交迭代的增量LLE算法，能有效的实现增量处理功能。以上都是采用的单点增值处理方法，该方法在处理数据时效率低，实时性差，容易造成数据不能及时处理，引起数据堆积。

文中采用一种基于增量流形学习的故障诊断方法，该方法通过流形学习算法对训练数据进行降维处理，得到初始流形结构，然后利用增量学习方法对新增数据进行状态分析，从而实现在线状态监测。最后通过对转子训练数据与测试数据的计算分析，验证了该方法能有效获得设备的实时运行状态及相关信息。

1 原理简介

1.1 局部切空间排列算法(LTSA)

由于训练样本数据通常比较少，会出现数据不完整现象，即数据集存在“空洞现象”，局部切空间排列算法能很好的处理“空洞”数据，能获得较好的嵌入效果[7]。因此，本文采用LTSA算法对转子高维故障数据集进行降维处理。

采用LTSA算法对训练数据进行降维处理时，选取邻域、局部坐标计算、低维嵌入坐标计算的时间复杂度与空间复杂度将随着训练数据的增加而成倍增长，该算法对训练数据进行批量处理非常耗时。在线监测将不断产生新数据，如何对新增数据与原始数据进行合理处理来达到既能很好的分析设备当前的状态，又能很好的降低数据处理的时间复杂度与空间复杂度将是需要研究的问题。

1.2 增量流形学习机制

故障监测与诊断过程中包含数据训练学习阶段和状态识别阶段。在训练学习阶段，通过对训练数据进行学习，得到用于模式辨识的低维嵌入流形结构，这种方式属于静态处理模式。当运行设备的信息数据源源不断的产生且需要及时分析处理时，面临如何有效处理新增数据的问题，为此学者提出了各种用于新增数据处理的方法，即动态增量学习方法[8]。该方法能较好的达到实时状态监测与故障诊断的要求。

1.3 特征生成

特征生成主要是为后续的特征选择以及特征压缩（降维）服务，常通过对消噪滤波后的数据进行线性处理来得到原始特征，如时域分析方法、频域分析方法[9]、小波分析方法[10]等。在特征生成过程中，若数据呈现出非线性特性，则可采用滑动时间窗进行预处理，将消噪滤波后的数据分割成长度相同的数据段，对每一段数据分别进行特征统计分析，构造出高维特征向量。对机械设备信号数据进行特征生成，既可以去除对故障识别不相干的噪声特征，又可以简化后续处理的复杂度。

1.4 增量局部切空间排列算法(ILTSA)

LTSA根据存在交叉片段的局部邻域中的特征信息来构造特征数据集的整体流形结构，它使高维嵌入空间与其内在低维流形空间中的近邻点保持着相同的近邻关系。任何数据点与它的近邻点具有“平移、旋转及伸缩”不变性，当观测数据不断增多时，使用平移、旋转以及伸缩变换对存在于高维空间的数据进行处理，使其得到的低维全局固有结构更加真实，这就是增量学习。其方法是：设数据集X={x1，x2，...，xn∈RD}作为已经通过LTSA学习获得了低维表示的训练数据集。设新增数据集Y={xn+1，xn+2，...，xn+m∈RD}，以便把新增数据的有用信息合理的融入到已有的低维模型结构中去。具体步骤如下：

step 1：对原始训练数据集X进行LTSA非线性降维学习，得到其低维流形嵌入坐标ZX={z1，z2，…，zn∈Rd}，d表示原始训练数据集X的本征维数。从新增数据集Y中找出k近邻全在X中的数据点xi放入X中，并求取这些点的正交投影其中j=1，2，…，k；xij为xi的第j个近邻点，xi为k个邻域点的均值，Qi是在xi的邻域矩阵中选择的一组正交基，通过对加入X中的新增数据点进行全局坐标重构，最后获得其低维嵌入坐标ZY→X={zn+1，zn+2，…，zn+b∈Rd}，其中b表示Y中数据的k近邻全在X中的数据点数；

step 2：从训练数据集X，Y中选出k邻域既包含X中的点也包含Y中的点的数据点，运用LTSA降维算法求出这些点对应的正交投影，从而获得全局坐标，最终得出它们的低维嵌入坐标ZXY={zn+b+1，zn+b+2，…，zn+b+p∈Rd}，p表示k邻域属于两个集合的数据点数；

step 3：用LTSA算法对新增数据集Y进行降维处理，得到的低维坐标ZY={y1，y2，…，ym∈Rd}，设集合Y中k近邻中既存在X中的点也存在Y中的点的d维表示为{yB1，yB2，…，yBq∈Rd}，其中Bq表示集合Y中属于边界点的数量；

最后，积极有效地进行反对历史虚无主义思潮教育。近年来，每逢抗战胜利纪念日等重要时间节点，片面抗战论、唯武器论等早在抗战时期就存在并被证明为错误的论调不时出现，起了怀疑和否定党的历史的作用。对于这一历史虚无主义思潮在抗战问题上的表现，各种纪念活动和纪念文章中对党在抗战中历史作用进行了反复阐述。

step 4：计算新增数据集Y的平移、旋转及伸缩变换：ynew=a(Ty+u)，其中T为旋转变换矩阵，u是平移向量，a是伸缩因子，要使下式最小：

修正下面中公式的min排列

其中Ti=[τi1，τi2，…，τik]，Li是待定映射矩阵。

要使Ei最小，即使Ei=Ti(I-k-1eeT)LiΘi最小。

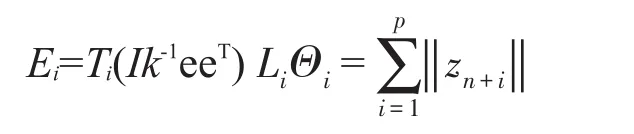
LTSA算法的各阶段采用顺序结构执行时，计算每一个数据点的k近邻，如果存在n个数据需要处理，即从高维数据到低维坐标的计算时间复杂度为O(d2n)，d为数据集的本征维数。文中提出的动态LTSA增量流形学习把原始训练数据集与现有新增数据集分别进行动态流形学习，从而发现整体数据集的低维嵌入坐标。最终的计算复杂度远小于传统流形学习方法，其时间复杂度为

2 应用仿真

2.1 算法的设计流程

本实验以转子实验台采集的振动信号数据作为原始数据进行分析。其中转子试验台如图1所示。

图1 转子试验台

首先在试验台上模拟转子的4种运行状态（转子正常状态、不平衡状态、不对中状态，碰磨状态），然后分别采用电涡流传感器、放大器、电路转换器以及采集卡在双跨转子转速为3 000 r/min，采样频率为5 000 Hz时对转子振动信号进行采集，对原始信号数据进行消噪滤波处理。得到如图2所示的四种状态下消噪后的波形图，四种状态下波形图略有区别，正常状态下波形图相对平稳，不平衡状态下波形有紧邻相同幅度二次杂波，不对着中状态下有小幅度二次杂波且整个波形幅值减小明显，碰磨状态下也存在小幅二次杂波。

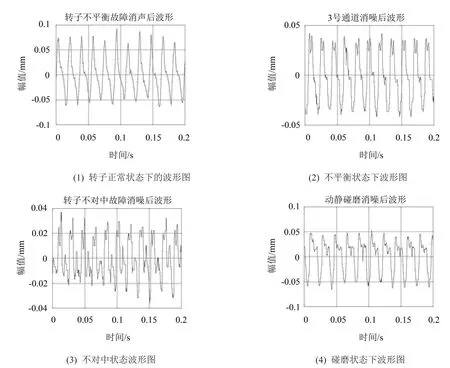
图2 四种不同状态的消噪后波形图

对12个通道采集的滤波后的数据进行特征生成。采用14个时域特征参数（均值、均方根幅值、标准差、方差、绝对均值、偏度、峭度、峰峰值、峰值指标、裕度指标、波形指标、C因素、均根方值、L因素等）来描述信号的特征信息并构造训练样本集。

流程图如图3所示，首先将采集到的转子4种状态下的原始数据分成两部分，分别进行滤波消躁处理。第一部分数据用于训练；第二部分数据定为新增数据集，用于增量式流形学习中。对4种状态的训练数据集进行特征生成得到时域特征。通过对所有状态的统计特征数据进行LTSA降维处理，获得训练数据的全局坐标矩阵与低维嵌入坐标。同理，对新增数据也进行特征生成获得其14个时域特征，将获得的特征数据与训练数据进行k近邻计算分析，达到对训练模型的修正与完善和对新增数据信息的及时采纳与补充，实现信息量越来越完整，越来越准确的目的。

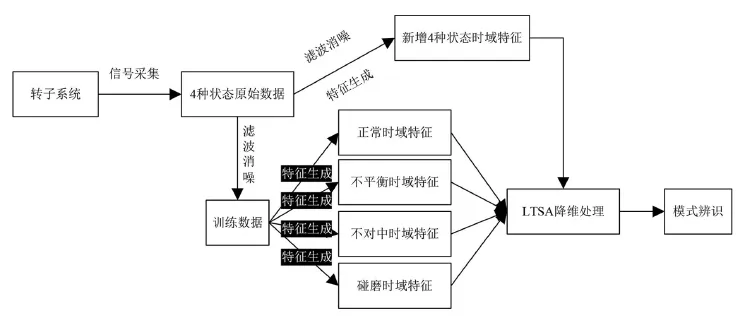
图3 增量式LTSA降维算法流程图

2.2 仿真结果及分析

图4是训练数据时域统计特征通过LTSA降维处理获得的四类低维特征数据，其中“○”代表正常特征数据点，“◇”代表不平衡数据点，“*”代表不对中数据点，“+”代表碰磨数据点，可以看到通过流形学习LTSA的降维处理，获得的不同类别的低维特征数据能很好的得到分离。图6是在训练数据的基础上增加了10个样本点的降维效果，可以看出新增数据并没有影响数据的分类。在新增数据的降维过程中，不仅将新增点的特征信息融入到了原来的训练模型中，而且完善了原始数据的分类模型，增强了模型的鲁棒性。图6、7分别是新增20个和新增40个特征数据的降维结果，分类效果略低于前面两种情况，但几种类型的数据仍然得到了较好的分离。类间距略大于前两种情况，类内距略小于前两种情况。为了进一步说明降维效果，文中采用聚类方法对降维后数据进行处理如表1所示。通过表1可以看出LLTSA降维后的数据所得的数据具有更好的聚类性。

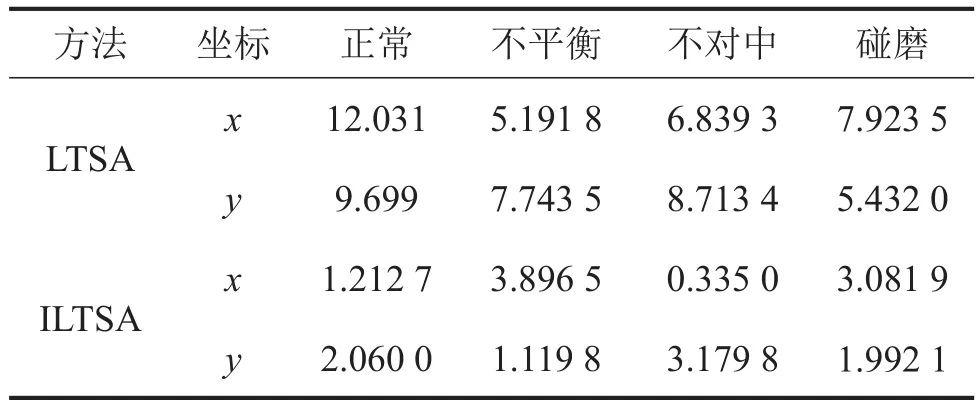
表1 数据聚类结果

图4 原始LTSA对四类数据的降维效果

从图中可以看出增量LTSA算法对新增数据有较好的识别能力。随机以一次数据作为分析准则，尽管数据有所增加，但各类数据的内类聚集度和识别度都较高。图中显示训练样本的低维嵌入坐标与新增数据的低维嵌入坐标变化不大，原因在于新增样本来源于原始类别基础上，且其低维坐标变化范围控制在训练样本的低维嵌入坐标内。图像略微的变化是由于新增样本改变了原始训练数据中部分数据的邻域。通过对比发现，新增数据量越大，其变化越明显。因此，在增量处理的过程中需要注意的是：在保持模式识别精度的情况下，尽可能扩大新增数据的容量，这样更有利于大数据的处理和满足智能诊断的要求。

图5 新增10个样本的降维效果

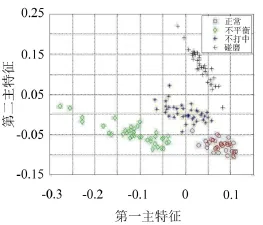
图6 新增20个样本的降维效果

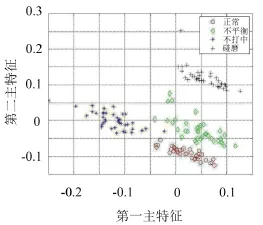
图7 新增40个样本的降维效果

3 结语

针对流形学习在新增数据和海量数据处理方面存在的不足，本文提出了一种增量学习算法。在此基础上详细介绍了几种最新的增量学习算法并受其启发，提出了增量LTSA流形学习算法。将该方法用于转子实验台4种不同状态的时域统计特征的学习中，发现该算法在保证降维精度的同时能较好的将新增数据的特征信息融入到已有分类模型中。为实时状态监测与智能诊断提供了一种可行性方法。

[1]Jia P,Yin J,Huang X,et al.Incremental laplacian eigenmaps by preserving adjacent information between data points[J].Pattern Recognition Letters,2009,30(16): 1457-1463.

[2]万鹏，王红军，徐小力.局部切空间排列和支持向量机的故障诊断模型[J].仪器仪表学报，2013，33(12)：2789-2795.

[3]杨庆，陈桂明，童兴民，等.增量式局部切空间排列算法在滚动轴承故障诊断中的应用[J].机械工程学报，2012，48(5)：81-86.

[4]Law M H C,Jain A K.Incremental nonlinear dimensionality reduction by manifold learning[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2006, 28(3):377-391.

[5]杨庆，陈桂明，江良洲，等.带标志点的LTSA算法及其在轴承故障诊断中的应用[J].振动工程学报，2013，25 (6)：732-738.

[6]朱明旱，罗大庸，易励群，等.基于正交迭代的增量LLE算法[J].电子学报，2009，37(1)：132-136.

[7]曾宪华，罗四维.动态增殖流形学习算法[J].计算机研究与发展，2007，44(9)：1462-1468.

[8]李文华.改进的线性局部切空间排列算法[J].计算机应用，2011，31(001)：247-249.

[9]唐新安，谢志明，王哲，等.风力机齿轮箱故障诊断[J].噪声与振动控制，2007，2(1)：120-124.

[10]花汉兵.基于小波包的振动信号去噪应用与研究[J].噪声与振动控制，2007，12(6)：19-21.

Application of Incremental Local Tangent SpaceAlignment Algorithm to Dimension Reduction for Rotor Failure Data Set

HU Chang-an1,YUAN De-qiang2,WANG Peng1,DU Wen-bo1
(1.National Institute of Measurement and Testing Technology,Chengdu 610021,China; 2.Lanzhou University of Technology,Lanzhou 730050,China)

The traditional learning algorithm does not have incremental learning ability,so it is unlikely to deal with additional new data and large data sets.In this paper,an incremental local tangent space alignment(LTSA)algorithm for mechanical rotor fault diagnosis was put forward.In this method,the LTSA algorithm was used for dimension reduction of the original training samples,and the corresponding low-dimension configuration was obtained.Then,using the incremental learning algorithm,the additional new samples were processed,and the embedded low-dimensional coordinates of the data were obtained.Finally,the rotor fault datasets verified the feasibility of the method,and a good classification effect was obtained.

vibration and wave;fault diagnosis;artificial intelligence;rotor;local tangent space alignment(LTSA) algorithm

TB53；TP206+.3；TP18；TN911.7

：A

：10.3969/j.issn.1006-1335.2015.01.047

1006-1355(2015)01-0230-05

2014－06－19

胡常安(1986－)，男，山东人，硕士，主要从事检测校准、无损检测、故障诊断研究。E-mail:ajitaiajitai@163.com