高铁板式轨道区段箱梁结构噪声辐射分析

石广田，杨新文，张小安，杨建近

（1.兰州交通大学 机电工程学院，兰州 730070； 2.同济大学 交通运输工程学院，上海 201804；3.兰州交通大学 数理学院，兰州 730070）

高铁板式轨道区段箱梁结构噪声辐射分析

石广田1，杨新文2，张小安3，杨建近1

（1.兰州交通大学 机电工程学院，兰州 730070； 2.同济大学 交通运输工程学院，上海 201804；3.兰州交通大学 数理学院，兰州 730070）

利用Simpack软件建立高速列车-轨道耦合动力学模型，计算在轨道不平顺谱激励下的轮轨垂向力，以此作为载荷边界条件施加到高架箱梁结构的有限元模型。计算了高架箱梁表面的振动响应，并利用箱梁结构振动响应作为声学边界条件。进而又采用间接边界元法对其进行声辐射分析。研究结果表明，利用板壳单元，采用有限元—边界元方法能够有效计算混凝土简支箱梁结构的振动噪声，主要集中在0～200 Hz的低频段，峰值主要出现在中心频率16 Hz、25 Hz与80 Hz～100 Hz；横向声场的声压级随着距离的增加而减小，频率越低越明显；垂向声场的声压级整体上随离地面距离的增加而增大，其中远场区域的声压级在低于31.5 Hz的频段内变化不大，在80 Hz～100 Hz频段内箱梁结构对其附近及上方区域的结构噪声大于其它区域，尤其是箱梁正上方。

声学；结构噪声；高速铁路；高架箱梁；板式轨道

近年来高速铁路技术不断的发展，列车通过高架桥梁结构的振动及结构噪声已越来越受到重视。Thompson及其团队成员[1]对铁路噪声进行了大量的研究，已取得了许多有意义的研究成果。翟婉明、蔡成标等[2，3]对车辆—轨道耦合动力学及车—线—桥动态相互作用问题进行了深入系统的研究，为我国的高速铁路技术做出了有价值的贡献。李小珍、张迅等[4，5]利用列车—轨道—桥梁耦合振动与稳态声辐射的边界元法、统计能量法理论，提出高速铁路桥梁结构噪声全频段预测方法，并以32 m双线混凝土简支箱梁为研究对象，对其进行现场测试及仿真分析。高飞等[6]采用有限元—边界法对城市轨道交通高架结构的振动与声辐射进行了分析研究。Augusztinovicz F等[7]对正交异性刚箱梁桥的结构噪声进行了分析研究。Ouelaa Nourdine等[8]通过考虑车桥耦合作用和轨道不平顺，将列车的每辆车只考虑两个自由度，利用三跨连续桥瞬态加速度作为单极子激励源计算声场声压。Ngai K W等[9]对香港某高架铁路混凝土箱梁进行了振动和噪声测试，得出当列车以140 km/h的速度运行时高架桥梁噪声和振动的频率范围在20 Hz～157 Hz之间。谢旭等[10]提出桥梁振动辐射低频噪声的计算方法，以一座简支钢桥进行分析和实测，对理论方法进行了验证，并对部分参数对其的影响进行了探索。雷晓燕等[11，12]利用美国高速铁路噪声预测方法，对其进行修正，得出了适用于我国客运专线、高速铁路环境噪声预测和评价的方法，并利用Ansys建立车辆—轨道—桥梁、桥梁—大地—建筑物耦合模型，对引起的环境振动进行了评价为连接线的减振设计提供依据。卢祝清等[13]在对城市轨道交通的噪声源特点进行分析的基础上，介绍噪声预测方法，并与国外的成熟方法进行了对比分析。李洪强[14]在分析城市轨道交通的噪声产生机理和传播规律的基础上，提出相应的控制措施和途径，为解决城市轨道交通发展中的噪声环境问题提供了一定的参考。

本文首先利用Simpack软件建立高速列车-轨道耦合动力学模型，得到了德国轨道低干扰谱激励下轮轨垂向力。以此轮轨垂向力，作为振动计算载荷边界条件施加到高架桥箱梁结构有限元模型，计算了高架桥梁表面的振动响应，并利用箱梁结构部分的振动响应作为声学边界条件，基于Helmholtz边界积分方程分析了箱梁结构的噪声辐射问题。

1 物理学模型

1.1 动力学分析模型

将车辆和无砟轨道整体看做一个耦合动力体系，两者动力学方程由车辆和轨道系统的运动方程分别为

式中M、C和K分别为质量、阻尼和刚度矩阵；u、u˙和¨分别为垂向位移、速度及加速度向量，其中下标v、t分别代表车辆和轨道结构；F为广义垂向荷载。

在轮轨系统中，不同的结构体系有各自相对应的运动方程，总体结构体系的运动方程为

图1 高速列车—无砟轨道耦合动力学模型

由于所分析的问题是一个大型复杂的非线性动力系统，求解车轨系统动力学响应采用积分方法，在计算过程中，时间积分步长为0.001 s。

利用Ansys软件建立轨道—桥梁有限元模型，将上述方法得到轮轨垂向力作为荷载边界条件施加到轨道—桥梁有限元模型中，采用有限元法进一步对箱梁结构的振动进行求解。

1.2 声学分析模型

对于非封闭的高架箱梁结构，通过计算边界表面两侧的Helmholtz积分方程差值可得声场中任意点的声压。结构在流体介质中振动，引发的声辐射问题满足声波波动方程、流固界面的诺依曼（Neumann）边界条件以及萨摩菲尔德（Sommerfeld）辐射条件，即

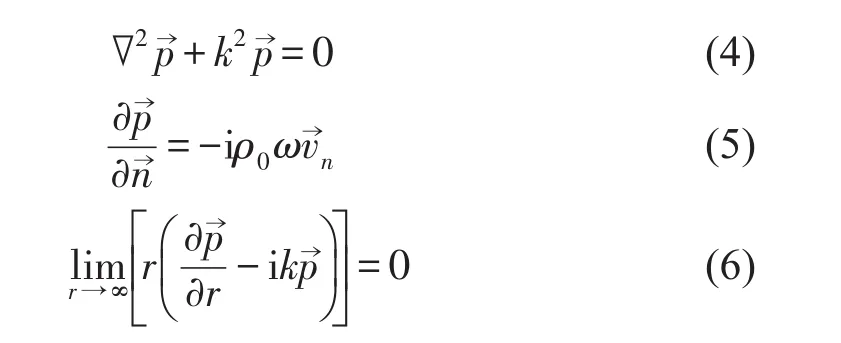
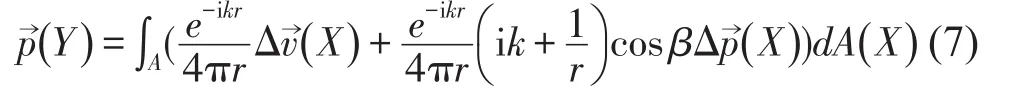
式中β为结构表面X点法向矢量与矢径r的夹角；D为流体域；Δv→(X)为X点表面两侧速度差；Δp→(X)为X点表面两侧声压差；分别表示为

利用边界单元离散结构表面，可得结构表面边界上各节点的两侧速度差和声压差为

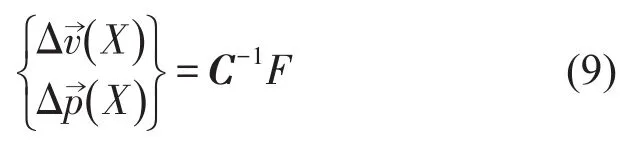
式中C为对称的复数满秩矩阵，同时也是激励频率的函数。影响因素主要包括结构表面的形状、尺寸和插值形函数，F为外激励的向量，取决于结构的表面振动速度。

2 数值分析

2.1 轨道—箱梁耦合振动有限元模型

张迅等[5]的研究表明：梁单元模型忽略了梁体局部振动的振动特性，高估了结构刚度特性；板单元能较好的反映结构整体及局部特性，适用于桥梁结构的声辐射分析研究。本文对于箱梁结构采用赋予实际厚度的板壳单元进行分析。

选取高速铁路中常用的简支混凝土单箱单室高架箱梁为研究对象，全长32 m，梁高3 m，顶板、腹板及底板的厚度分别为0.315 m、0.480 m及0.3 m；桥上采用CRTS-I双线板式无砟轨道结构，轨道板长4.93 m，宽2.4 m、厚0.2 m，钢轨类型为60 kg/m。轨道—箱梁耦合振动有限元模型如图2所示，表1和表2分别给出了有限元模型的动力学参数及单元类型，网格大小都为0.3 m。

图2 板式轨道—箱梁耦合振动有限元模型

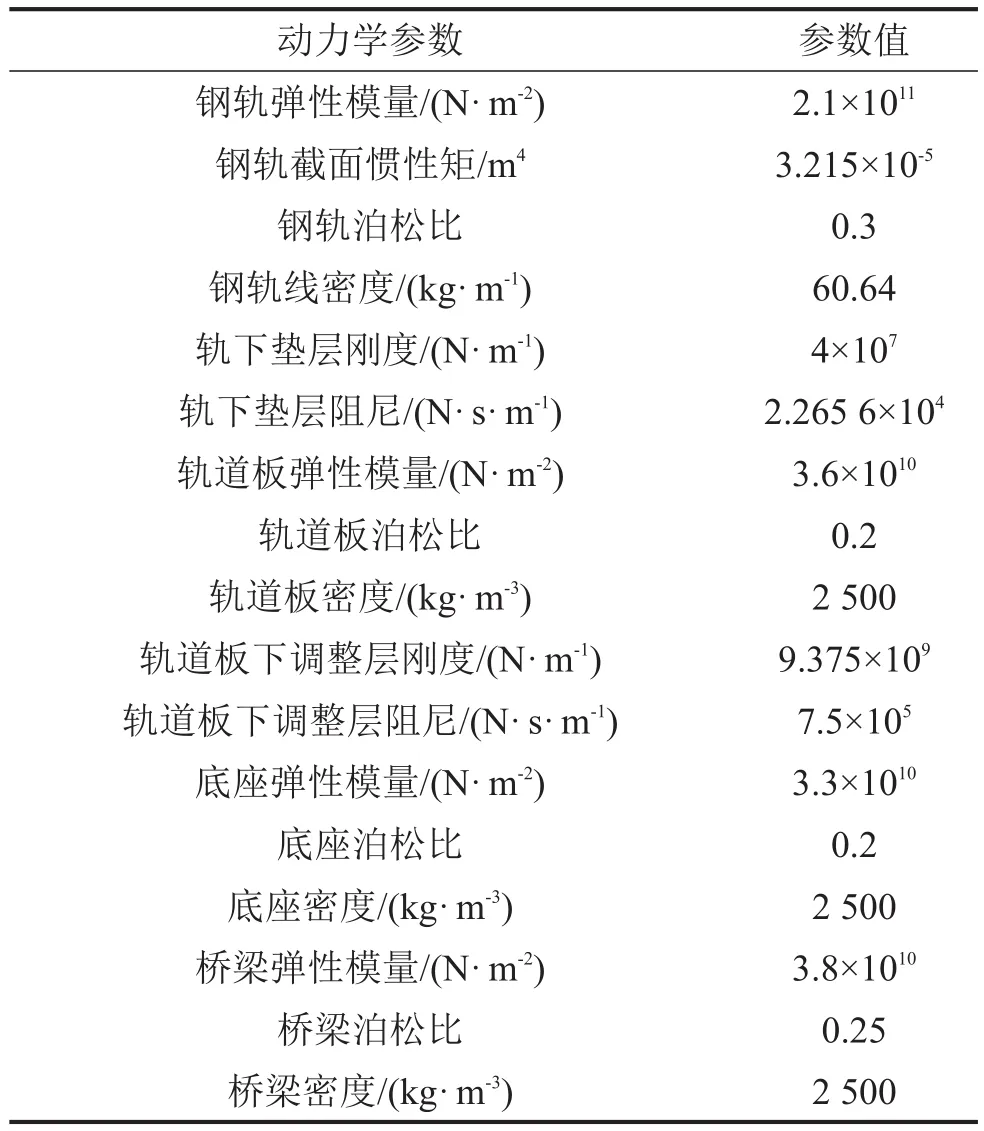
表1 轨道和桥梁动力学参数

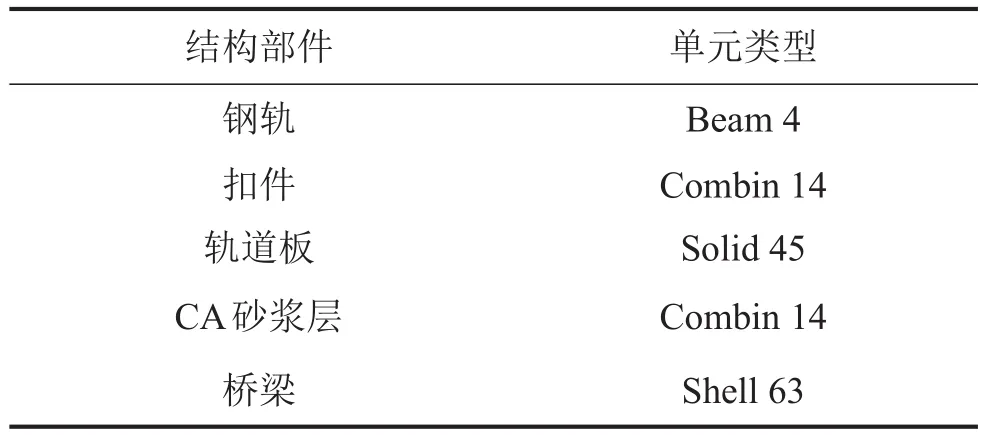
表2 有限元模型单元类型

2.2 箱梁结构动力学响应

当一列8节车辆编组的高速动车组以时速200 km/h通过高架桥，只考虑轮轨的垂向接触，车辆参数参见文献[2]附录3。图3给出了列车在轨道不平顺谱激励下左右侧竖向轮轨力。

由图3可知，轮轨力在60 kN附近波动，最大值可达到108.28 kN，车轮2的轮轨力整体上略大于车轮1。左右侧轮轨力相比，右侧较大。

利用Ansys软件，以上述轮轨垂向力作为荷载边界条件，施加到CRTS-I板式无砟轨道-箱梁有限元模型对箱梁的振动响应进行求解。图4给出了箱梁各板件中心位置节点的垂向加速度响应。

由图4可知，顶板的振动与腹板及底板相比较最为明显，三者振型基本一致；从频谱曲线可知，箱梁结构的振动频率主要集中在0～200 Hz的低频段，峰值大多出现在10 Hz～100 Hz。

2.3 箱梁结构噪声辐射

由于本文主要分析箱梁结构产生的噪声辐射，忽略轨道系统的结构噪声及其他噪声的影响。

将Ansys软件中建立的箱梁有限元模型及其振动响应结果导入Virtual.Lab软件。提取箱梁有限元模型表面网格作为声辐射分析的边界元网格。将箱梁结构每一处的振动加速度响应通过离散FFT进行时频转换，然后在1/3倍频程频段范围内作离散FFT逆变换，并计算此频段内的振动有效值，再将箱梁结构各个节点不同自由度方向的振动响应投影到其法车单线运行，箱梁两侧的声场分布并不对称，频率较低时，声场的指向性较强，随着频率的增大，辐射噪声的分布呈现复杂性；当频率为80 Hz～100 Hz时，箱梁附近，尤其是其上方区域的噪声辐射明显增大。

箱梁的结构噪声主要集中在0～200 Hz，当中心频率为16 Hz、25 Hz和80 Hz～100 Hz时，箱梁结构产生了明显的噪声峰值；桥底场点的声压级随离地面距离的增加而增大，在80 Hz～100 Hz内，箱梁附近的结构噪声明显大于其他场点；横向场点的声压级随着距离的增加而减小，频率越低越明显；远场场点的声压级在低于中心频率31.5 Hz的频段内变化不大，在80 Hz～100 Hz时，箱梁上方的噪声大于线方向，最后将箱梁结构的振动加速度响应转移到边界元网格，作为声辐射边界条件对箱梁结构的噪声辐射进行分析。假设桥梁墩高为20 m，分析场点选取列车运行侧1/2跨中垂向43 m，横向50 m范围内的声场区域，如图5所示。

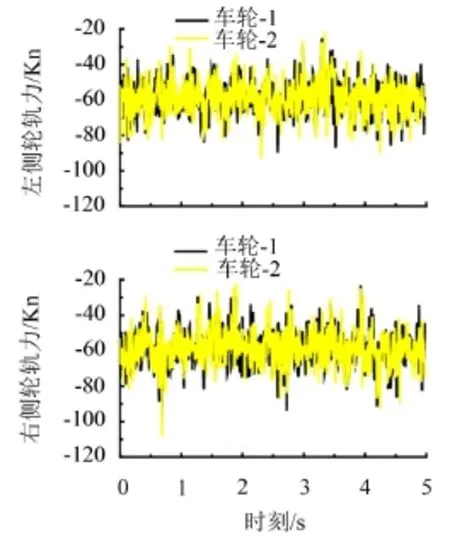
图3 200 km/h竖向接触轮轨力

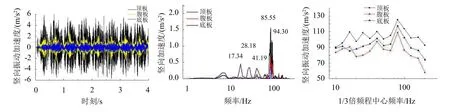
图4 1/2跨中中心桥梁结构振动加速度响应

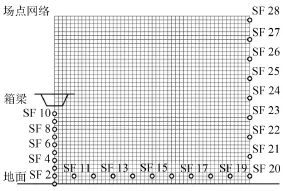
图5 场点分布图

图6给出了列车以200 km/h通过桥梁时，桥梁结构噪声线性计权和A计权声压级对比。A计权声压级明显不能真实体现箱梁结构产生的低频噪声，频率越低越明显，甚至低于平均声压，两者之间的最大差值约为70 dB，不能很好的预估低频噪声对人体的影响。因此本文采用线性计权声压级进行分析。

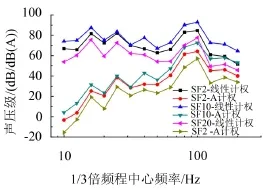
图6 线性/A计权声压级对比

图7和图8分别给出了跨中二维声场分布云图及所选场点的声压级（SPL）曲线。由图可知，箱梁的结构噪声在结构正上方及正下方比较密集。由于列其下方噪声，在这一频段内，图7与图8的分析结果相对应，因此箱梁结构的辐射噪声对其上方区域的影响强于下方区域。

3 结语

（1）利用板壳单元，采用有限元—边界元方法能够有效计算混凝土简支箱梁结构的振动与噪声问题，主要集中在0～200 Hz的低频段，峰值出现在10 Hz～100 Hz；

（2）在中心频率为16 Hz、25 Hz和80 Hz～100 Hz时出现了明显的噪声峰值。横向声场的声压级随着距离的增加而减小，频率越低越明显。垂向声场中声压级整体上随离地面距离的增加而增大，其中远场区域的声压级在低于31.5 Hz的频段内变化不大，在80 Hz～100 Hz频段内箱梁结构对其附近及上方区域的结构噪声大于其它区域，尤其是箱梁正上方。

图7 跨中二维声场分布云图

图8 时速200 km/h场点声压级频谱曲线

[1]Thompson D J.Railway noise and vibration-mechanisms, modeling and means of control[M].Amsterdam:Elsevier Ltd.,2009.

[2]翟婉明.车辆—轨道耦合动力学（第三版）[M].北京：科学出版社，2007.

[3]蔡成标.高速铁路列车—线路—桥梁耦合振动理论及应用研究[D].成都：西南交通大学，2004.

[4]李小珍，张迅.高速铁路桥梁结构噪声的全频段预测研究（I）：理论模型[J].铁道学报，2013，35(1)：101-107.

[5]张迅，李小珍.高速铁路32 m简支箱梁声辐射特性研究[J].铁道学报，2012，34(7)：96-102.

[6]高飞，夏禾.用边界元—有限元法研究高架结构辐射噪声[J].土木建筑与环境工程，2012，34(1)：42-46.

[7]Augusztinovicz F,Marki F,Nagy A B,et al.Derivation of train track isolation requirement for a steel road bridge based on vibro-acoustic analyses[J].Journal of Sound and Vibration,2006,293(3/4/5):953-964.

[8]Ouelss Nourdine,Rezaiguia Abdelouahab,Laulagnet Bemard.Vibro-acoustic modeling of a railway bridge crossed by a train[J].AppliedAcoustics,2006,67(5):461-475.

[9]Ngai K W,Ng C F.Structure-borne noise and vibration of concrete box structure and rail viaduct[J].Journal of Sound and Vibration,2002,255(2):281-297.

[10]谢旭，张鹤，等.桥梁振动辐射低频噪声评估方法研究[J].土木工程学报，2008，41(10)：53-59.

[11]雷晓燕，罗锟.高速铁路噪声预测方法研究[J].噪声与振动控制，2008，(5)：132-137.

[12]雷晓燕，，刘庆杰，，朱成九，等.高架轨道诱发环境振动预测与评价研究[J].噪声与振动控制，2008，(6)：108-135.

[13]卢祝清，刘林芽，黄志和.高速铁路噪声预测方法及其在昌九城际轨道交通中的应用[J].噪声与振动控制，2009，(3)：82-85.

[14]李洪强，吴小萍.城市轨道交通噪声及其控制研究[J].噪声与振动控制，2007，(5)：78-82.

Noise RadiationAnalysis of Box-girder Structure in Slab Track Section of High Speed Railways

SHI Guang-tian1,YANG Xin-wen2,ZHANG Xiao-an3,YANG Jian-jin1
（1.School of Mechatronic Engineering,Lanzhou Jiaotong University,Lanzhou 730070 China; 2.School of Transportation Engineering,Tongji University,Shanghai 201804,China; 3.School of Mathematics and Physics,Lanzhou Jiaotong University,Lanzhou 730070,China）

A high speed train-track coupling dynamics model was established using Simpack software,and the wheel/ rail vertical contact force excited by track irregularity spectrum was calculated.The wheel/rail vertical force was taken as a boundary condition and applied to the finite element model(FEM)of an elevated box girder structure to calculate its surface vibration response.Then,the vibration response was taken as the acoustic boundary conditions and was applied to the boundary element model(BEM)of the elevated box-girder structure to analyze its sound radiation.The results show that,using the finite element method and the boundary element method,the vibration noise of the concrete simply-supported box-beam structure can be effectively calculated with shell elements.The vibration noise is mainly concentrated in the low frequency range of 0-200 Hz,and the peaks mainly appear at the central frequencies of 16 Hz,25 Hz,80 Hz-100 Hz.The sound pressure level decreases with the increase of the distance from the ground in the lateral sound field and this tendency is more obvious for lower frequency sound field.The sound pressure level generally increases with the increase of the distance from the ground in the vertical acoustic field,and the sound pressure level in far field area does not change obviously for the frequencies below 31.5 Hz.In the range of 80 Hz-100 Hz,the sound pressure levels of the field points near the girder,especially above the girder,are higher than those in the other regions.

acoustics;structuce noise;high speed railway;elevated box girder;slab track

TB132；TB532

：A

：10.3969/j.issn.1006-1335.2015.01.033

1006-1355(2015)01-0160-05

2014－05－05

国家自然科学基金资助项目(51165017)

石广田（1962－），男，甘肃天水人，工学博士，教授，主要研究方向：高速铁路噪声研究与控制。E-mail:zxaazxy@163.com