非参数回归模型中误差方差的样条估计

武新乾, 张 刚

(河南科技大学 数学与统计学院 河南 洛阳 471023)



非参数回归模型中误差方差的样条估计

武新乾, 张 刚

(河南科技大学 数学与统计学院 河南 洛阳 471023)

针对具有固定设计和混合相依误差的非参数回归模型，构造了误差方差的多项式样条估计，证明了估计量的相合性，并且通过模拟算例说明了估计方法的可行性．

非参数回归； 误差方差； 样条估计； 混合； 相合性

0 引言

非参数方法在回归建模中具有灵活性，受到了许多学者的关注[1-5]．考虑非参数回归模型

Yi=m(xi)+εi,i=1,…,n，

(1)

其中，xi=i/n为固定设计点，Yi为响应变量，m(x)为未知回归函数，{εi}是均值为0、方差为σ2的平稳序列．

样条方法是一种常见的非参数估计方法．文[6]在φ-混合和α-混合误差下讨论了m(x)的B-样条估计的全局收敛性和一致收敛性，类似文献可参见文[7-10]．作者主要构造模型(1)中误差方差的多项式样条估计，在文[6]中的混合误差条件下证明误差方差估计量的相合性,模拟结果表明了方法的可行性．

1 样条估计

首先给出文[6]中回归函数m(x)的样条估计．记Sk,v表示在区间[0,1]上具有k+1个等距结点(包括两个区间端点)的v次样条函数空间，其B-样条基函数记为Bkt(x) (t=1,…,k+v)．又记K=k+v，(·)′表示向量的转置．令

Bk(x)=(Bk1(x),Bk2(x),…,BkK(x))′，

回归函数m(x)的样条估计为

(2)

(3)

2 主要结果

研究估计量的性质需要文[6]中的如下条件：

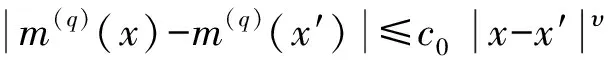
(ⅱ)k=O(N1/(2p+1))，0

(4)

I1=oP(N-2(r-δ))．

(5)

又

和

这里φn(j)=φ(jN/n)，αn(j)=α(jN/n)．于是有

所以，

I3-σ2=OP(N-1/2)，

(6)

这也说明I3=OP(1)．由于

因此，

I2=oP(N-(r-δ))OP(1)=oP(N-(r-δ))．

(7)

综合(4)～(7)式可得

即

(8)

3 模拟算例

对于非参数回归模型(1)，选用文[11]中的回归函数m(x)=50x3(1-x)3，x∈[0,1].考虑两种随机误差序列{εi}：(I)εi独立同分布并且εi～N(0,0.64);(II)εi=0.5εi-1+ei，{ei}为独立同分布序列，且ei～N(0,0.48)．这两种随机误差序列均满足定理1的条件，并且它们的方差相同，σ2=Var(εi)=0.64．

选取ε0=0，采用三次B-样条基函数构造估计量，并且基于AIC和BIC准则从1～10之间自动选择k值，其中，

AIC=ln(RSS/n)+2K/n; BIC=ln(RSS/n)+ln(n)·K/n，

(9)

表1 情形(I)下误差方差σ2的典型估计及其绝对误差Tab.1 Typical estimates of error variance σ2 and their absolute errors under (I)

注：括号内数据为绝对误差值.

表2 情形(II)下误差方差σ2的典型估计及其绝对误差Tab.2 Typical estimates of error variance σ2 and their absolute errors under (II)

注：括号内数据为绝对误差值.

图1 BIC准则下误差方差σ2的样条估计的盒形图Fig.1 Box plots of spline estimates of error variance σ2 under BIC

[1] Robinson P M．Large-sample inference for nonparametric regression with dependent errors [J]．The Annals of Statistics，1997，25 (5)：2054-2083．

[2] Park C G，Kim I，Lee Y S．Error variance estimation via least squares for small sample nonparametric regression [J]．Journal of Statistical Planning and Inference，2012，142 (8)：2369-2385．

[3] Qiu D，Shao Q，Yang L．Efficient inference for autoregressive coefficients in the presence of trends [J]．Journal of Multivariate Analysis，2013，114(2)：40-53．

[4] 孙耀东，徐宝，赵志文．固定设计下时间序列非参数回归模型的方差变点检验[J]．郑州大学学报：理学版，2014，46(1)：1-4．

[5] 李佳，李永明．PA误差下的半参数回归模型估计的矩相合性[J]．信阳师范学院学报：自然科学版，2013，26(1)：23-26．

[6] Burman P．Regression function estimation from dependent observations [J]．Journal of Multivariate Analysis，1991，36 (2)：263-279．

[7] Wahba G．Bayesian “confidence intervals” for the cross-validated smoothing spline [J]．Journal of the Royal Statistical Society: Series B，1983，45(1)：133-150．

[8] Zhou S，Shen X，Wolfe D A．Local asymptotics for regression splines and confidence regions [J]．The Annals of Statistics，1998，26 (5)：1760-1782．

[9] Mao W，Zhao L H．Free-knot polynomial splines with confidence intervals [J]．Journal of the Royal Statistical Society: Series B，2003，65(4)：901-919．

[10]武新乾．线性过程误差下回归函数的样条估计[J]．河南科技大学学报：自然科学版，2010，31(5)：94-97．

[11]Tran L，Roussas G，Yakowitz S，et al．Fixed-design regression for linear time series[J]．The Annals of Statistics，1996，24 (3)：975-991．

(责任编辑：孔 薇)

Spline Estimate of Error Variance in Nonparametric Regression Models

WU Xin-qian， ZHANG Gang

(SchoolofMathematicsandStatistics,HenanUniversityofScienceandTechnology,Luoyang471023,China)

Nonparametric regression models with fixed design and mixing dependent errors were considered. A polynomial spline estimate of error variance was constructed, and weak consistency of the estimator was proved. Meanwhile, the feasibility of the estimation was illustrated by a simulated example.

nonparametric regression； error variance； spline estimate； mixing； consistency

2015-04-11

国家自然科学基金资助项目，编号11326181；河南省国际科技合作计划项目，编号134300510034；河南科技大学博士科研启动基金资助项目，编号4010-13480008．

武新乾(1969-)，男，河南中牟人，副教授，博士，主要从事非线性时间序列分析及应用研究，E-mail:wuxinqian1001@163.com．

武新乾,张刚.非参数回归模型中误差方差的样条估计[J].郑州大学学报：理学版，2015,47(3)：17-20.

O212.7

A

1671-6841(2015)03-0017-04

10.3969/j.issn.1671-6841.2015.03.003