“复式双曲线”型问题探微

□王美兰魏祖成

“复式双曲线”型问题探微

□王美兰魏祖成

在同一坐标系中的两条不同的双曲线，我们称之为“复式双曲线”.以“复式双曲线”为载体的试题，融入了丰富的数学知识和数学思想，结构独特，思维含量高，呈现形式新，现列举几例，从不同角度入手，归纳出这类问题的解题策略.

一、利用面积求值

例1如图1，以O为中心的平行四边形ABCD的顶点A、C在双曲线上，B、D在双曲线上，k1＝2k2（k1＞0），AB∥y轴，S▱ABCD＝ 24，则k1＝__________.

图1　

解析：利用平行四边形的性质设A（x，y1）、B（x，y2)，根据反比例函数的图象关于原点对称的性质可知C（－x，－y1）、D（－x，－y2）.由反比例函数图象上点的坐标特征，将点A、B的坐标分别代入它们所在的函数图象的解析式，求得y1＝－2y2，最后根据·2x＝24，可以求得k2＝y2x＝4，故k1＝8.

图2　

（1）求双曲线y1与y2的解析式；

（2）若平行于x轴的直线l交双曲线y1于点A，交双曲线y2于点B，在x轴上存在点P，使以点A，B，O，P为顶点的四边形是菱形，求点P的坐标.

图3　

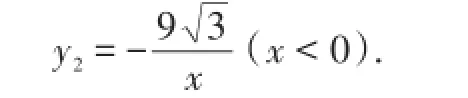
（2）因为双曲线y1与y2关于y轴对称，所以点A与点B关于y轴对称，有OA＝OB.设，则，AB＝2m，因为四边形OPAB是菱形，则OB＝AB，∴OA＝AB＝OB，所以△OAB是等边三角形.所以∠AOB＝60°，设AB交y轴于E，则∠AOE＝30°，所以，m＝±3.又m＞0，所以m＝3，所以P（6，0）.同理，当四边形OABP是菱形时，P（－6，0）.综上所述，满足要求的点P有P（6，0）或P（－6，0）.

二、利用k求面积

图4　

A.2B.3C.4D.5

图5　

解析：分别过A、B作x轴垂线，垂足分别为E、F，则S▱ABCD＝S▱AEFB＝5.

A.5B.6C.7D.8

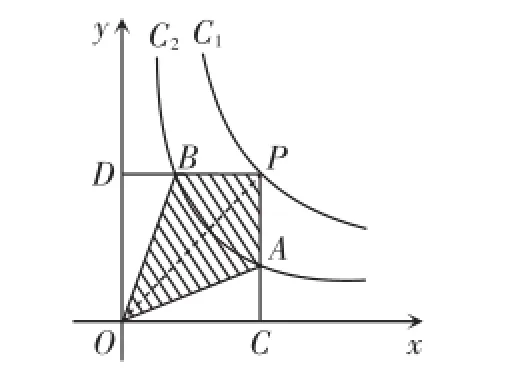
图6　

解析：连接OP，由反比例函数系数k的几何意义可求出△OPC及△OAC的面积分别为3和，进而可得出△OPA的面积为同理△OPB的面积也为，所以四边形PAOB的面积为5，故选A.