适用于光伏多峰功率跟踪的改进型粒子群优化算法

胡克用,胥芳,艾青林,欧阳静,徐红伟

(1.浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室,310014,杭州; 2.杭州师范大学钱江学院,310036,杭州)



适用于光伏多峰功率跟踪的改进型粒子群优化算法

胡克用1,2,胥芳1,艾青林1,欧阳静1,徐红伟1

(1.浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室,310014,杭州; 2.杭州师范大学钱江学院,310036,杭州)

针对在自然环境下光伏阵列上时常发生的局部阴影而引起P-V曲线由单峰转变成多峰状态,从而导致常规最大功率跟踪算法失效的问题,在研究传统粒子群算法的基础上,提出了一种改进型控制算法。该算法采用全局模式和局部模式两种运行手段定位最大峰值点,在对粒子群优化的速度更新方式上,去除了大量的随机变量干扰,使结构优化非常明显。改进后粒子群优化算法能够使功率跟踪避免陷入局部最优,使之找到真正的最大功率点。通过与传统粒子群算法对比仿真及试验,结果表明,在光伏阵列局部遮荫的情况下,改进后的粒子群优化算法可以快速准确地搜索到最大功率点,追踪精度高达95%,并且比传统的粒子群算法在搜索效率上提升28%,较好地避免了陷入局部最优。

局部阴影;最大功率跟踪;粒子群算法;光伏阵列

迄今为止,中国仍有2 000多万的无电人口,主要分布在边远落后的农村地区,特别在中国西北,由于电力供应不足,地下水开采利用率很低,有些地方至今没有解决饮水与灌溉问题。同时,西北农村地区的太阳辐射强,日照时间长,土地面积宽广,非常适合利用太阳能来发电,往往一个小规模光伏发电站就能满足单个农村的用电来源。

然而,在光伏发电的过程中,如何提高效率是面临的主要问题,其中提高效率的举措之一就是最大功率点的跟踪(MPPT)控制,其控制实质就是一个自动寻优的过程[1-2],但在实际应用中会遇到很多问题,阴影遮挡就是其中主要问题之一。由于天气的不断变化,特别是云团飘过给地面光伏阵列带来的阴影遮挡时常都在发生[3],于是光伏P-V曲线呈现出多峰轮廓的状态,由几个局部峰值(LP)和一个全局峰值(GP)构成,导致常规的MPPT算法(如爬山法[4]、扰动法[5-7]和导纳增量法[8-10]等)容易陷入局部最优,而非真正的最大功率点。

针对此问题,国内外学者们纷纷提出了自己的解决方案。文献[11]基于离散时间纹波控制算法,通过对纹波控制技术的离散化处理,将最大功率点跟踪转换为离散采样-控制问题。文献[12]采用嵌入式智能光伏模块,提出统一输出最大功率跟踪控制策略。文献[13]采用差分进化算法进行二阶段的全局最大功率点搜索,但只提出了算法的实现思想,未通过实际试验加以验证。文献[14-16]提出了通过人工神经网络与模糊逻辑控制算法相结合的方式进行全局最大功率点跟踪,此方法先采用3层前向反馈网络进行训练,再模糊逻辑控制确定电压,但之前需要大量的准备工作,比如说变量模糊化、规则库建设、推理机制及去模糊化操作。文献[17-19]提出了利用Fibonacci序列算法来跟踪最大峰值点,但该算法难以实现在部分阴影遮挡下的全局峰值搜索,应用局限性较大,同时由于计算开销较大,还需要配备一颗强大的处理器芯片。相比较而言,采用粒子群算法(PSO)进行最大功率的追踪[20-22],搜索效率高,在工程应用中算法较易实现。然而,问题在于PSO算法中随机变量太多,容易使粒子收敛于局部峰值点,同时自由的随机性也极大地降低了搜索效率。另外,PSO算法中的扰动量必须控制适度,如果太小,不足以把功率点推向预定值,使得迭代次数增多,如果太大,容易飞出全局峰值点,而陷入局部峰值点附近。

鉴于此,本文研究的是一种适用于光伏多峰功率跟踪的改进型粒子群优化算法,该算法包含全局模式和局部模式2种运行方式,先以全局模式快速逼近可能存在的GP位置,接着通过逐一对比,确定GP的大致位置,然后以局部模式精确定位最大峰值点。在对粒子群优化的速度更新方式上,去除了大量的随机变量干扰,只留下惯性权重值进行调节,便于对算法进行控制,优化结构非常明显。改进后的粒子群优化算法能使搜索粒子快速地从局部峰值点处脱离,避免陷入其中,提高了收敛效率。最后,本文把传统的PSO算法与改进后的优化算法进行最大功率跟踪对比,经过仿真分析以及试验验证表明,改进后的粒子群优化算法在局部遮荫情况下更能够快速且准确地实施光伏最大功率跟踪。

1 遮荫下的光伏电池特性

1.1 遮荫情况下的等效模型

在均匀日照情况下,由于电池单体是串联的,因而流经整个电池组件的电流是相同的,假设第1个电池单体被遮光时,如图1所示。

当第1个电池单体被阴影遮挡时,光生电流Isc迅速降为0,二极管反向偏置并使Id也降为0,则电流通过Rp和Rs而产生压降。被遮光后电压变成

Vc=-(Rp+Rs)I

(1)

式中:Rp为光伏电池并联等效电阻;Rs为光伏电池串联等效电阻;I为光伏电池输出电流。Vc为负值,这部分电压需要从整个电池组件中去除,这部分压降将消耗在被遮光的电池上而形成热斑。热斑的出现不仅降低了组件的输出功率,而且会减少电池的使用寿命。一种较好的用于保护电池的措施,就是在串联阵列中使用旁路二极管,使多余的电流绕过电池。

(a)遮荫下的物理模型 (b)遮荫下的电路模型图1 遮荫情况下的等效模型

1.2 遮荫下的电气特性

为了简化说明遮荫下的电气特性,采用2个光伏组件串联构成的PV阵列,假设1个光伏电池组件被充分日照,另1个被局部遮荫。在这样的情况下,由于连接方式是串联,流过2个光伏组件的电流是相同的,被遮荫的组件产生的电流小于被完全日照下的组件,于是多余电流会流过旁路二极管,组件的I-V特性如图2所示。

(a)未被遮荫 (b)被遮荫光 (c)串联组合的 光伏组件 伏组件 光伏组件 图2 多峰式光伏阵列特性

由图2可见,当未被遮荫的与被遮荫的光伏组件经过串联组合,由于日照的不同而导致输出电压产生多峰,从而造成总的输出功率产生多个峰值点。如果光伏组件的数量增加,在遮荫条件下的特性曲线会更加复杂,产生2个或更多个峰值点。在这种情况下,很难通过常规方式来追踪到最大功率点。

2 改进型粒子群优化在MPPT中的应用

2.1 传统的粒子群算法

粒子群算法的数学描述如下:每个粒子i包含为一个N维的位置向量xi=(xi1,xi2,…,xiN)和速度向量vi=(vi1,vi2,…,viN),当粒子i搜索解空间时,保存其搜索到的最优经历位置pi=(pi1,pi2,…,piN)。在每次迭代开始时,粒子根据自身惯性和经验及群体最优经历位置pg=(pg1,pg2,…,pgN)来调整自己的速度向量以调整自身位置。其中,每个粒子的位置和速度更新按下式计算

(2)

(3)

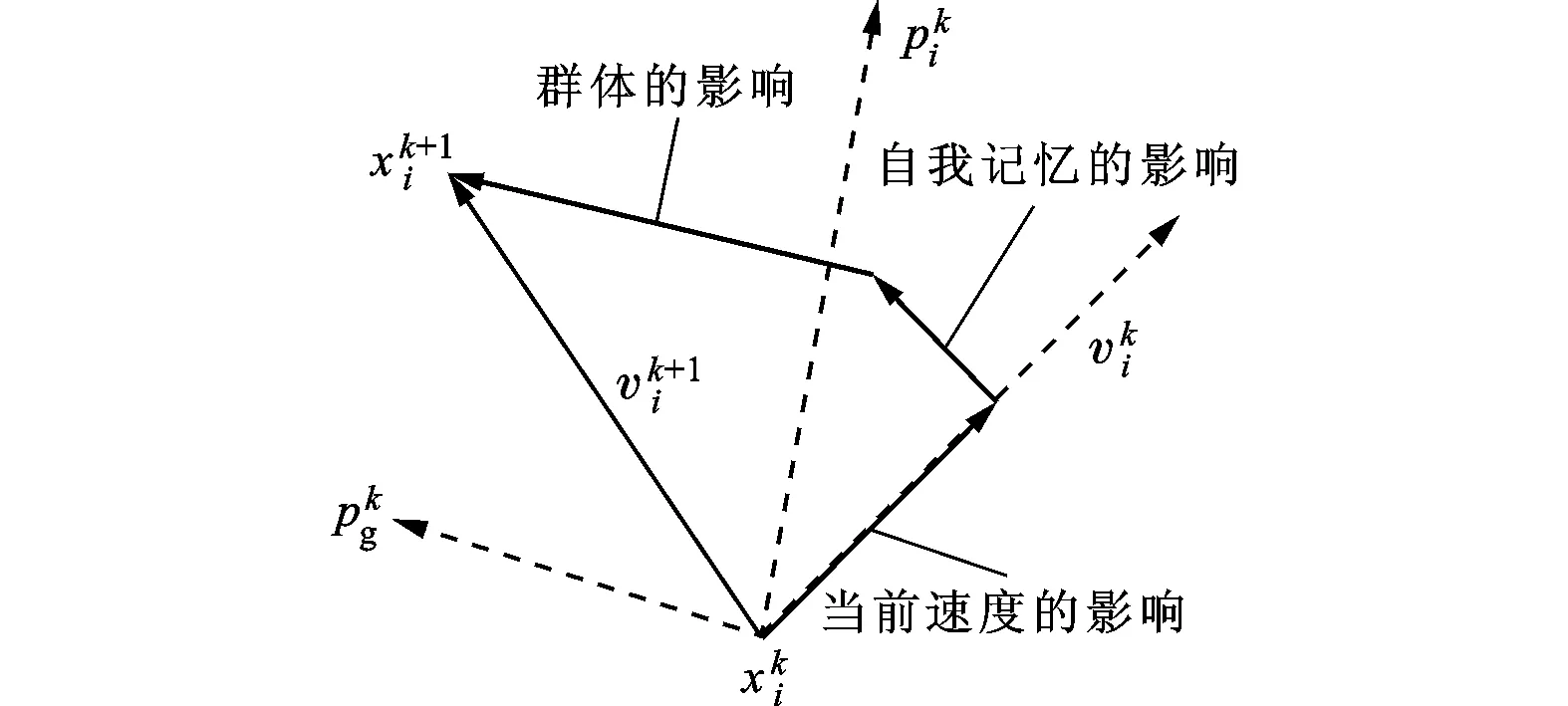
图3 粒子位置的更新方式

由于粒子群算法采用基于邻域的搜索技术,能够利用较小的种群数来保证足够的多样性,按并行方式搜索最优解。同时,粒子群算法的通用性比较好,适合处理多种类型的目标函数和约束,并易于与传统的优化方法相结合,从而改善自身的局限性。因此,本研究将粒子群算法加以改进,并应用于遮荫状态下的光伏最大功率跟踪上,具有很大的优势。

2.2 改进型粒子群优化算法

传统的粒子群优化算法应用于光伏最大功率跟踪系统存在着一个基本问题,从式(2)、式(3)可以看出,粒子群位置的更新会参考随机数的变化,故而存在2个不可控的因素。

(1)当随机数变化较大时,粒子群速度变化剧烈,容易使粒子跳出全局峰值附近区域,收敛于局部峰值点,这样粒子群的寻优就陷入了局部最优,而目前常规的MPPT算法很难区分全局最优和局部最优点。

(2)当随机数变化较小时,粒子群速度的更新不明显,要完成粒子群位置上的跃迁就显得非常缓慢,于是需要多次迭代才能达到目标点,造成计算开销成倍上升。

因此,为了解决以上难题,本文研究的是一种粒子群优化的改进型算法,该算法去除了式(2)中的随机因素以及限制峰值之间的速度因素,先是快速地对P-V曲线进行扫描,定位可能的GP位置,然后以扰动方式逼近最优解。修改之后的速度方程可以写成

(4)

这样转换有以下好处:

(1)由于去除了随机数的干扰,粒子群的寻优轨迹趋向于一致,即使只有少数粒子也能够快速定位全局峰值的可能位置;

(2)和传统粒子群算法相比,结构优化明显,变量中只有惯性权重需要调节,使粒子群的寻优过程变得更加可控;

(3)为应对多变的天气情况,设置vmax为速度因子,vmax的改变会影响迭代时占空比的变化,一般由用户设定,当遇到多云等光伏面板上阴影遮挡易发的天气,速度因子vmax可适当减小,这样更容易精确定位最大功率点。

2.3 算法的实现

在改进型粒子群优化算法中,本文采用2步法最大功率跟踪控制策略,即整个控制过程包含全局模式和局部模式,算法流程如图4所示。

(a)全局搜索模式

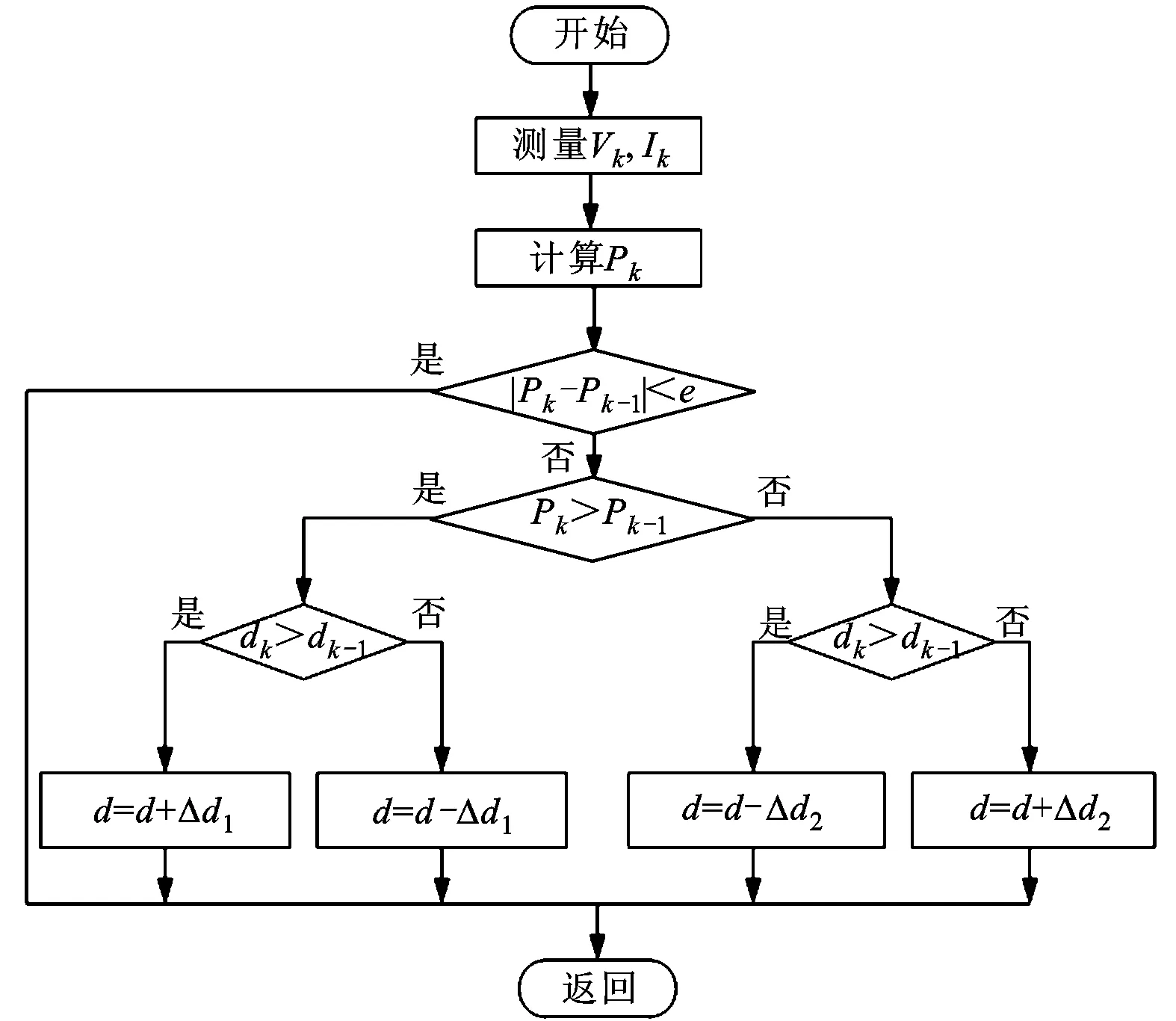
(b)局部搜索模式图4 局部阴影下的光伏MPPT控制流程

在常规情况下,环境变化比较缓慢,比如说太阳辐照正常波动,算法就以局部模式运行,通过给占空比d一个增量Δd,用来调节功率P,因为在附近就存在最大功率点。另一方面,当环境变化比较迅速时,比如说有云团飘过导致光伏阵列上产生了阴影遮挡,全局模式就会被激活,算法进入快速收敛通道,以固定的逼近操作模式搜索潜在的最大功率点位置,通过逐一对比,确定最大功率点的大致位置。一旦全局峰值点的大致位置被成功定位,算法就立即切换回局部模式,应用带变量扰动的爬山法,从而进一步得到最大功率点的精确解。

2.3.1 启动条件 在确定算法何时启动时,首先要定义群体中N颗粒子的占空比向量如下

dg=[d1,d2,d3,…,dN]

(5)

优化模型的目标函数需要满足

(6)

速度向量初始化为0,占空比最小值dmin和最大值dmax的计算式如下

(7)

(8)

式中:η是转换器的效率;RLmax、RLmin是连接端输出负载的最大、最小值。RPVmax、RPVmin是PV阵列的最大、最小阻抗。

自然环境变化的因素众多,为了避免控制算法频繁启动而造成大量的计算开销,需要区别是自然状态改变(如太阳辐射波动),还是由于云团飘过或房屋树木等产生的光伏板上的阴影遮挡,要进行以下判断

(9)

(10)

2.3.2 参数调整 本文对传统的粒子群算法进行了优化处理之后,只有一个参数即惯性权重需要调节,采用线性递减权值(LDW)策略,即随着迭代次数的增加,惯性权重因子不断减小,w满足

(11)

惯性权重的取值可从0.9到0.4线性递减,这样做的好处在于,在刚开始时,搜索粒子可以探索较大的区域,以尽可能快的速度定位最优解的大致位置。随着迭代次数的上升,惯性因子慢慢变小,搜索粒子的收敛速度也相应减小,开始精确定位最优解的位置。

2.3.3 终止策略 由于算法的多次迭代会引起功率振荡,从而降低了光伏输出效率。为了使最大功率搜索过程尽快收敛,本文采取了强制型终止策略。根据算法的特点,起初各个粒子分散在不同的位置,随着迭代次数的上升,各个粒子会逐渐往某一位置靠拢,当达到一定的聚集程度,就可以认为粒子已经到达最优解的附近。当粒子间的电压差最大值不超过0.5%Voc时,停止迭代,即满足结束条件。

3 仿真分析

3.1 仿真模型

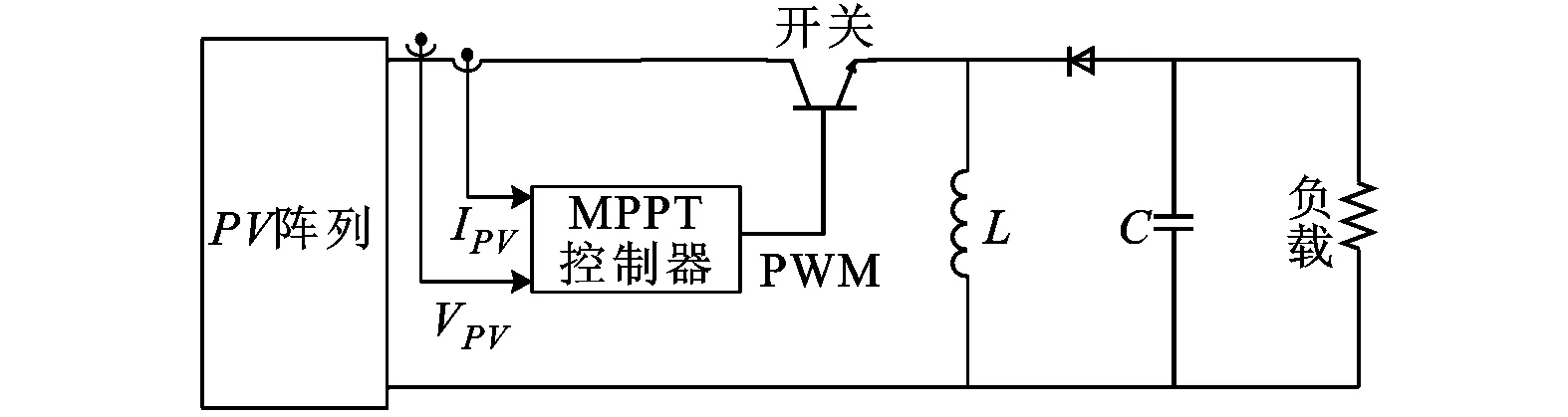
本文采用的是Matlab2011b软件平台进行系统仿真,使用BP Solar公司定制的光伏电池组件Solarex-MSX60数据进行建模,数据手册中标称参数Pmax=60 W,Vmp=17.1 V,Imp=3.5 A,Isc=3.8 A,Voc=21.1 V。参考温度设置为25 ℃,参考光照设置为1 kW/m2。光伏阵列的最大功率点跟踪系统如图5a所示,该buck-boost变换电路参数设置为C=200 μF,L=1.2 mH,f=60 kHz。

MPPT模块使用S-Function函数编写控制程序来实现对光伏阵列的最大功率点跟踪,并通过改变光伏电池的辐照度G和温度T等参数来模拟光伏阵列上发生阴影遮挡的情况,使P-V曲线产生多峰状态,如图5b所示。然后,在MPPT模块中输入传统的粒子群算法和改进型的粒子群算法2种控制策略,在Matlab的XY Graph模块中观察这2种控制策略的跟踪效果。

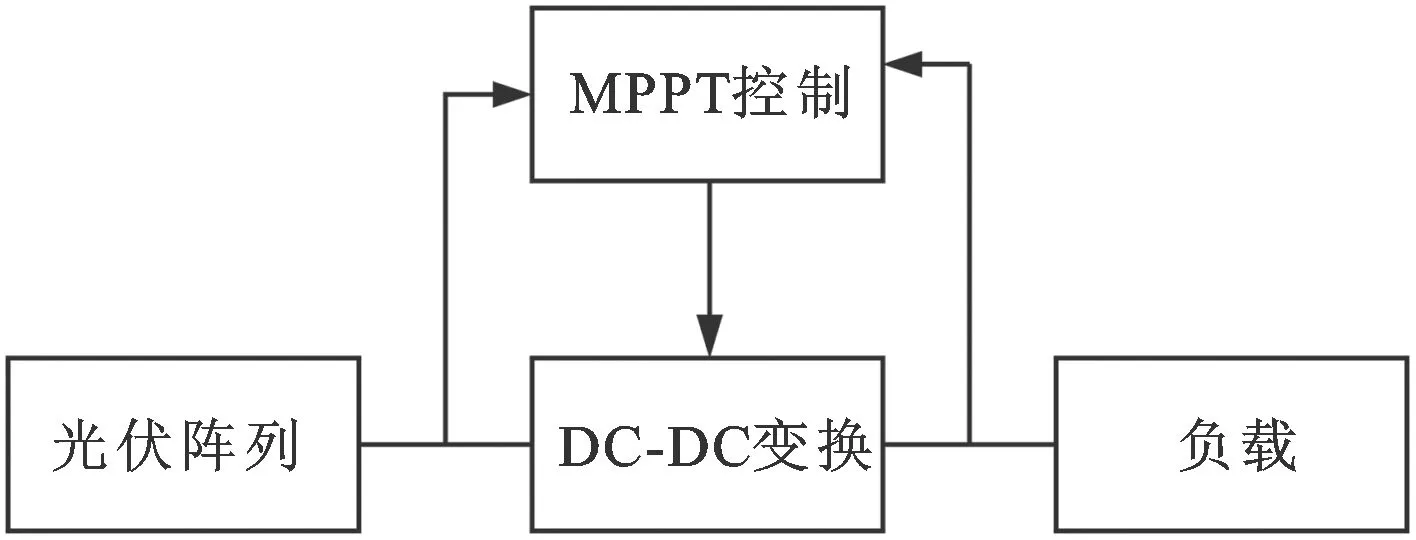
光伏阵列在局部阴影遮挡下的最大功率点跟踪过程的基本原理如图5c所示。DC-DC变换器的输入阻抗的大小可以通过MPPT算法控制开关电源的占空比加以实现,使得光伏阵列端口的等效负载发生变化,从而导致光伏阵列端口输出电压也发生相应变化,达到跟踪最大功率点的目的[23]。

(a)仿真模型

(b)阴影遮挡下的P-V曲线

(c)最大功率点跟踪原理图5 PV阵列的MPPT仿真分析

3.2 仿真结果对比分析

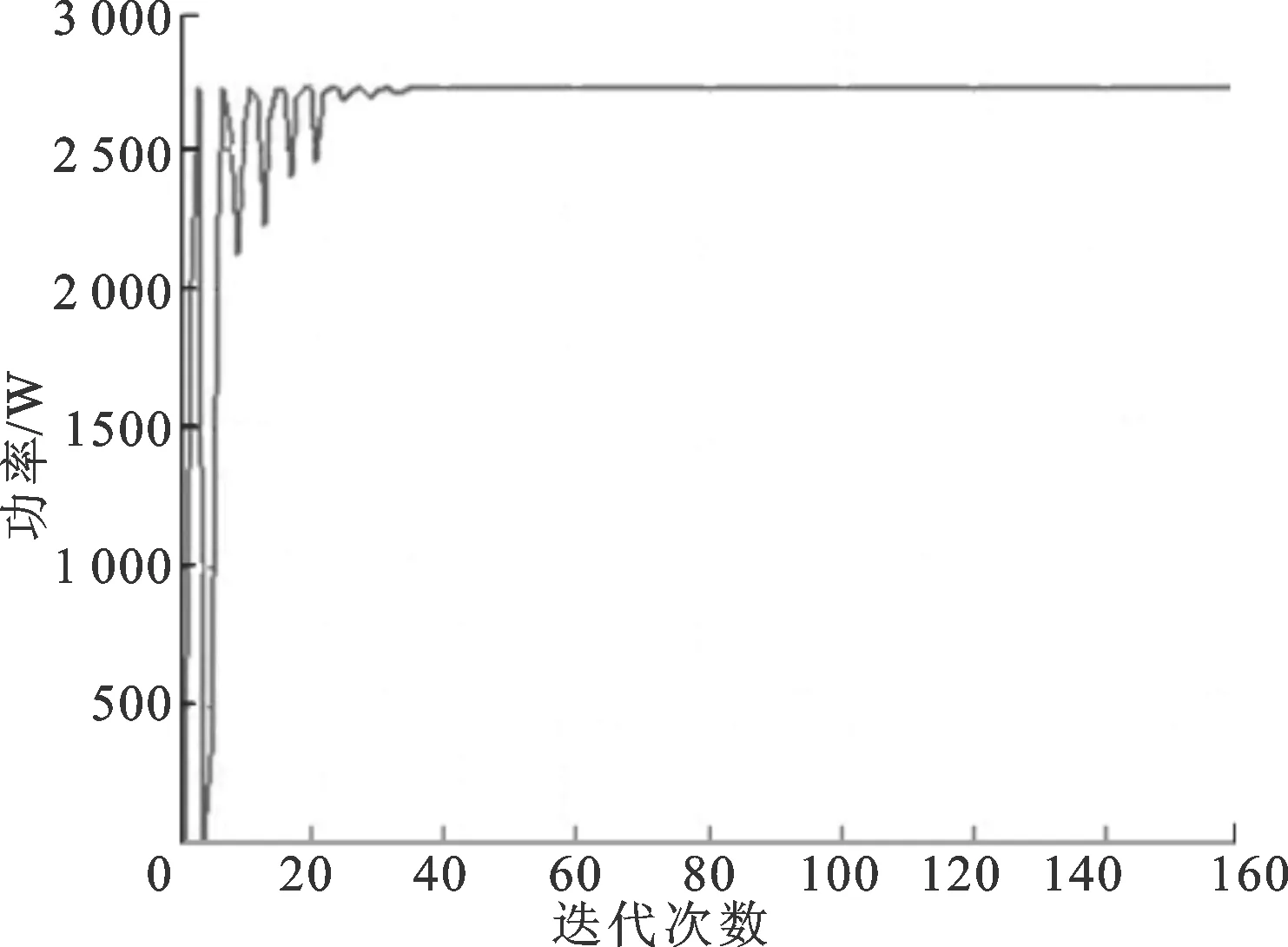
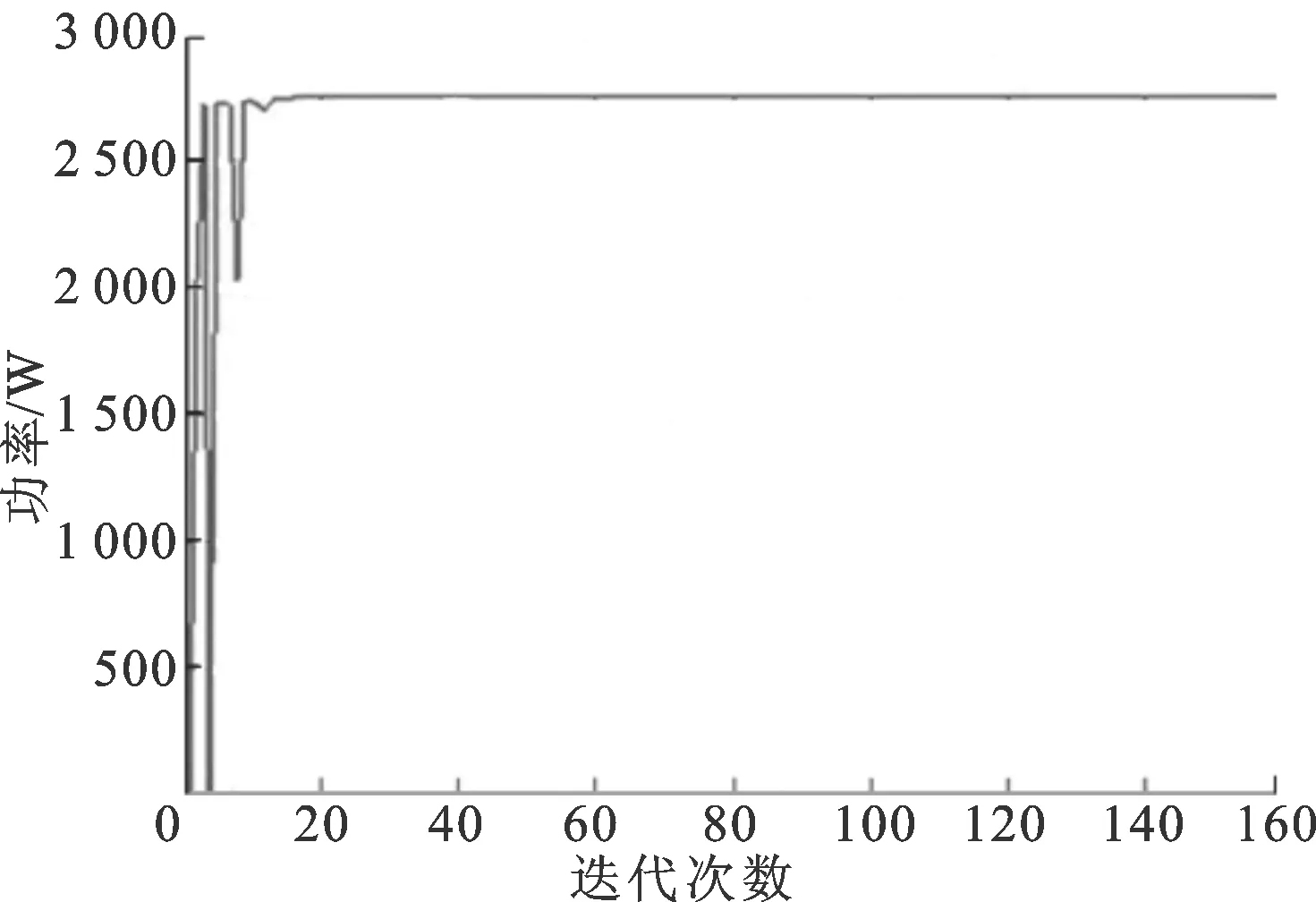
当光伏阵列受到阴影遮挡时,在粒子数分别为4和30的情况下,传统的粒子群算法和改进型的粒子群算法的功率跟踪仿真效果见图6。

从图6a、图6b可以看出,当粒子数为4时,2种算法的迭代次数分别经过35次和15次之后达到收敛。从图6c、图6d可以看出,当粒子数为30时,2种算法的迭代次数分别经过350次和120次之后达到收敛,可见改进型粒子群优化算法在提升收敛速度的效果上非常明显。另外,从图6中还可以发现,当参与算法的粒子数目较多时,收敛速度的提升效果更加显著。

(a)粒子数为4时的传统PSO算法

(b)粒子数为4时的改进型PSO算法

(c)粒子数为30时的传统PSO算法

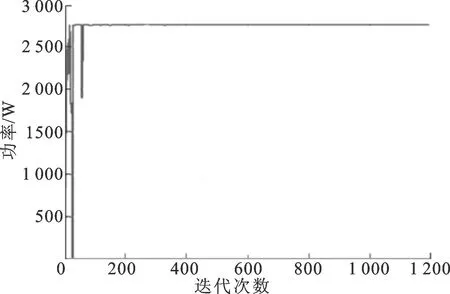
(d)粒子数为30时的改进型PSO算法图6 多峰状态下的功率跟踪效果仿真分析

另一方面,粒子数的增多,也会更加逼近实际的最大功率点。当粒子数为4时,该算法追踪到的最大功率为2 742 W,与实际最大功率2 750 W相差8 W,相对误差为0.3%;当粒子数为30时,该算法追踪到的最大功率为2 746 W,与实际最大功率2 750 W相差4 W,相对误差立即降到0.15%。

通过仿真分析可以看出,在光伏阵列受到阴影遮挡时,改进型粒子群优化算法能够有效准确地跟踪到最大功率点,并极大提升了跟踪速度。当然,虽说粒子数目的增多可以更加准确地逼近实际最大功率值,但是这是以牺牲跟踪速度和计算开销为代价的,因而在实际运用中需要进行折中处理。

4 试验验证

4.1 试验平台

为了对本文改进型算法进行试验验证,保证算法的实际可行性,搭建了一套光伏功率跟踪试验平台。该试验平台的硬件环境是由80 W光伏组件、MPPT控制电路、DSP2812、遮挡物构成;软件环境是由CCS3.3和基于VC++编写的功率监测控件构成,软硬件通信采用RS232串口。搭建的试验平台实物装置如图7所示。

图7 光伏MPPT试验平台

4.2 试验结果对比分析

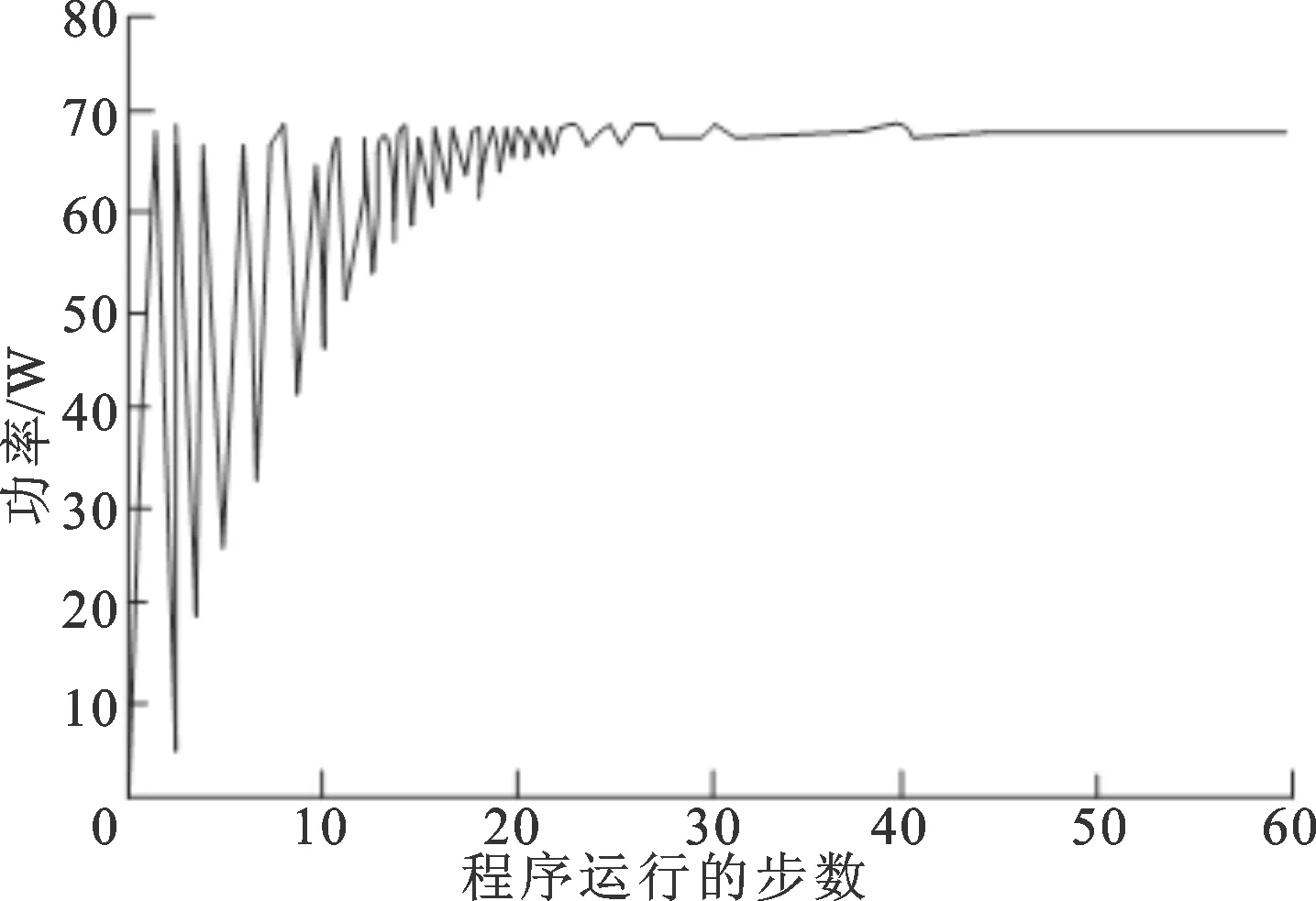
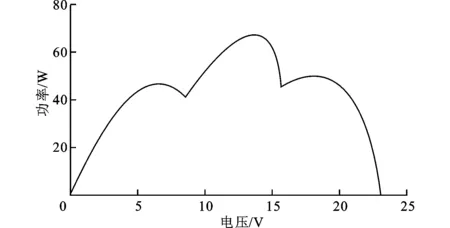
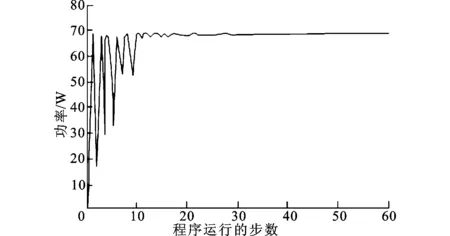
由于光伏组件与一个规模光伏阵列具有类似的结构特性,为了简便起见,本研究中通过手动遮挡光伏组件中的部分单元来模拟光伏阵列被阴影遮挡的情况,使输出功率上具有多峰值的特性。在DSP2812中通过设定PWM1的通用定时器周期值EvaRegs.T1PR为1 000,比较值EvaRegs.CMPR1从0开始每步递增20直至1 000,对光伏电池两端电压进行扫描。接着上位机采集此时的功率和电压变化,绘制出了在无阴影遮挡和有阴影遮挡条件下的P-V曲线,如图8a、图8b所示。然后,分别发送给传统的粒子群算法与改进后的粒子群优化算法,使DSP2812分别采用这2种算法进行最大功率点跟踪,并由RS232串口实时采集输出的功率数据,并经过PC上位机动态绘图,得到受阴影遮挡触发后的2种算法控制下最大功率跟踪曲线,如图8c、图8d所示。

(a)未遮荫下的P-V单峰曲线

(b)传统PSO算法下的功率跟踪曲线

(c)遮荫下的P-V多峰曲线

(d)改进型PSO算法下的功率跟踪曲线图8 多峰状态下的功率跟踪曲线

在同样的试验环境下运行2种算法,可以看出改进后的粒子群优化算法在搜索速度方面明显优于传统的粒子群算法,2种算法下的程序运行步数分别为32步和23步达到收敛,改进后优化算法在搜索效率上提升了28%。

另一方面,为了检验该优化算法运行的稳定性,本研究中分别对2种算法进行了30次重复试验,统计结果如表1所示。

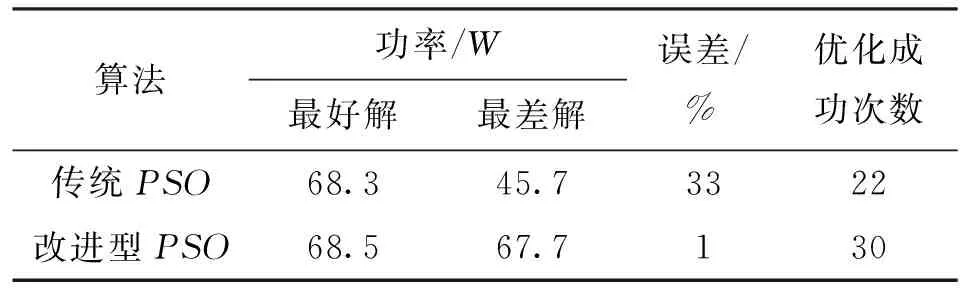
表1 优化结果统计与比较

由于粒子群每次优化前的初始状态都不同,因而尽管外界试验环境相同,跟踪到的功率值也会有小幅变化,所以在表1统计的数据中,设置了一个阈值,规定每次优化的结果与最好解之间的误差若小于5%,则表示优化成功。这样在反复30次的试验中,传统PSO算法下运行优化成功次数为22次,成功率为73%,能搜索到的最好解为68.3 W,最差解为45.7 W(这时陷入了局部峰值点),两者差距为33%。

对改进后粒子群优化算法也同样进行30次试验,优化成功次数达到30次,成功率为100%,能搜索到的最好解为68.5 W,最差解为67.7 W,二者差距仅为1%,搜索结果比较稳定,而且追踪到的最大功率点与光伏电池的最大功率点高度基本吻合,追踪精度高达95%。试验结果表明,采用改进后的粒子群优化算法进行光伏阵列阴影遮挡下的最大功率跟踪,运行效果稳定,而且明显改善了传统粒子群算法中容易陷入局部峰值点的弊端。

5 结 论

本文采用一种改进型的粒子群优化算法来跟踪光伏阵列的最大功率点,在日常的光伏功率跟踪上,使用局部模式进行常规的功率跟踪。当遇到光伏阵列有阴影遮挡等特殊情况时,启动全局模式与局部模式相结合的控制方式,快速定位最大功率点。

(1)通过研究传统粒子群算法,面对光伏面板阴影遮挡下P-V曲线产生的多个峰值,采用全局搜索与局部搜索相结合的功率跟踪策略,并给出了具体的实现方案。

(2)为了提高粒子群的优化速度,在速度更新方式上,去除了大量的随机变量干扰,使结构优化非常明显,从而加快了搜索的收敛速度。

(3)通过仿真分析与试验测试,改进后的粒子群优化算法与传统的粒子群算法对比,在阴影遮挡条件下对光伏最大功率点追踪精度高达95%,在搜索效率上提升了28%,并且不容易陷入局部最优点。

[1]BRITO DE M A G, GALOTTO L, SAMPAIO L P, et al.Evaluation of the main MPPT techniques for photovoltaic applications [J].IEEE Transactions on Industrial Electronics, 2013, 60(3):1156-1167.

[2]YAMADA H, KIMURA K, HANAMOTO T, et al.A novel MPPT control method of thermoelectric power generation with single sensor [J].Applied Sciences, 2013, 3(2):545-558.

[3]李盼, 吴江, 管晓宏, 等.分析光伏电站输出特性的云遮挡太阳辐射模型 [J].西安交通大学学报, 2013, 47(8):61-67.LI Pan, WU Jiang, GUAN Xiaohong, et al.Solar radiation model with cloud influence for stochastic characteristics analysis of large-scale photovoltaic power plant output [J].Journal of Xi’an Jiaotong University, 2013, 47(8):61-67.

[4]张小莲, 李群, 殷明慧, 等.一种引入停止机制的改进爬山算法 [J].中国电机工程学报, 2012, 32(14):128-134.ZHANG Xiaolian, LI Qun, YIN Minghui, et al.An improved hill-climbing searching method based on halt mechanism [J].Proceedings of the CSEE, 2012, 32(14):128-134.

[5]ABDELSALAM A K, MASSOUD A M, AHMED S, et al.High-performance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids [J].IEEE Transactions on Power Electronics, 2011, 26(4):1010-1021.

[6]文韬, 洪添胜, 李震, 等.太阳能硅光电池最大功率点跟踪算法的仿真及试验 [J].农业工程学报, 2012, 28(1):196-201.WEN Tao, HONG Tiansheng, LI Zhen, et al.Test and simulation of solar silicon battery tracking algorithm based on maximum power point [J].Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(1):196-201.

[7]唐磊, 曾成碧, 苗虹, 等.基于切线角的光伏变步长最大功率跟踪控制策略 [J].电力系统自动化, 2013, 37(20):28-33.TANG Lei, ZENG Chengbi, MIAO Hong, et al.A new control strategy for MPP tracking in photovoltaic system based on contingence angle and variable step-size searching method [J].Automation of Electric Power Systems, 2013, 37(20):28-33.

[8]MEI Q, SHAN M, LIU L, et al.A novel improved variable step-size incremental-resistance MPPT method for PV systems [J].IEEE Transactions on Industrial Electronics, 2011, 58(6):2427-2434.

[9]MIRBAGHERI S Z, MEKHILEF S, MIRHASSANI S M.MPPT with inc.cond method using conventional interleaved boost converter [J].Energy Procedia, 2013, 42(1):24-32.

[10]董密, 杨建, 彭可, 等.光伏系统的零均值电导增量最大功率点跟踪控制 [J].中国电机工程学报, 2010, 30(21):48-53.DONG Mi, YANG Jian, PENG Ke, et al.Zero average incremental conductance maximum power point tracking control for photovoltaic system [J].Proceedings of the CSEE, 2010, 30(21):48-53.

[11]刘圣波, 刘贺, 赵燕东.基于离散时间纹波控制的太阳能最大功率点跟踪算法 [J].农业工程学报, 2013(19):130-137.LIU Shengbo, LIU He, ZHAO Yandong.A solar maximum power point tracking algorithm based on discrete-time ripple correlation control [J].Transactions of the Chinese Society of Agricultural Engineering, 2013 (19):130-137.

[12]王丰, 吴新科, 卓放.嵌入式智能光伏模块的最大功率输出统一控制 [J].中国电机工程学报, 2013, 33(21):81-89.WANG Feng, WU Xinke, ZHUO Fang.Application of unified output MPPT control in DMPPT PV systems [J].Proceedings of the CSEE, 2013, 33 (21):81-89.

[13]简献忠, 严军, 范建鹏, 等.基于差分进化算法的光伏阵列MPPT控制方法 [J].控制工程, 2014, 21(4):559-562, 566.JIAN Xianzhong, YAN Jun, FAN Jianpeng, et al.MPPT control method of photovoltaic array based on differential evolution algorithm [J].Control Engineering of China, 2014, 21(4):559-562, 566.

[14]KARATEPE E, HIYAMA T.Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions [J].IET Renewable Power Generation, 2009, 3(2):239-253.

[15]ALAIMI B N, AHMED K H, FINNEY S J, et al.Fuzzy-logic-control approach of a modified hill-climbing method for maximum power point in microgrid standalone photovoltaic system [J].IEEE Transactions on Power Electronics, 2011, 26(4):1022-1030.

[16]EL KHATEB A H, RAHIM N A, SELVARAJ J.Fuzzy logic control approach of a maximum power point employing SEPIC converter for standalone photovoltaic system [J].Procedia Environmental Sciences, 2013, 17(1):529-536.

[17]RAMAPRABHA R, MATHUR B, RAVI A, et al.Modified Fibonacci search based MPPT scheme for SPVA under partial shaded conditions [C]∥2010 3rd International Conference on Emerging Trends in Engineering and Technology.Piscataway, NJ, USA:IEEE, 2010:379-384.

[18]RAMAPRABHA R, BALAJI M, MATHUR B L.Maximum power point tracking of partially shaded solar PV system using modified Fibonacci search method with fuzzy controller [J].International Journal of Electrical Power and Energy Systems, 2012, 43(1):754-765.

[19]TUMBELAKA H H, MIYATAKE M.Simple integration of three-phase shunt active power filter and photovoltaic generation system with Fibonacci-search-based MPPT [C]∥2010 IEEE Symposium on Industrial Electronics and Applications.Piscataway, NJ, USA:IEEE, 2010:94-99.

[20]MIYATAKE M, TORIUMI F, FUJII N, et al.Maxi-mum power point tracking of multiple photovoltaic arrays:a PSO approach [J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1):367-380.

[21]ZHOU T, SUN W.MPPT control method of PV system with PSO algorithm based on minimal particle angles [C]∥Proceedings of the 2012 International Conference on Information Technology and Software Engineering.Berlin, Germany:Springer, 2013:755-763.

[22]ZHAO Yahong, ZHAO Xuecheng, ZHANG Yunhui.MPPT for photovoltaic system using multi-objective improved particle swarm optimization algorithm [J].TELKOMNIKA Indonesian Journal of Electrical Engineering, 2014, 12(1):261-268.

[23]任航, 叶林.模拟分析环境因素对小型太阳能发电系统运行特性的影响 [J].电工技术学报, 2010, 25(10):158-165.REN Hang, YE Lin.Operation characteristics of PV system under the influence of environmental factors [J].Transactions of China Electrotechnical Society, 2010, 25(10):158-165.

(编辑 杜秀杰)

Improved Particle Swarm Optimization for Photovoltaic Multi-Peak Power Tracking

HU Keyong1,2,XU Fang1,AI Qinglin1,OUYANG Jjing1,XU Hongwei1

(1.Key Laboratory of E&M, Ministry of Education & Zhejiang Province, Zhejiang University of Technology, Hangzhou 310014, China; 2.Hangzhou Normal University Qianjiang College, Hangzhou 310036, China)

The partial shade on photovoltaic array appears repeatedly in natural environment to change single peak into multi-peaks inP-Vcurve.An improved algorithm following the traditional particle swarm optimization is proposed, where the global mode and local mode are adopted to locate the maximum power point.To accelerate the speed of particle swarm optimization, a lot of random and interfered variables are removed to realize an obvious structure optimization.The improved particle swarm optimization algorithm prevents power tracking from falling into the local optimum, and finds the true maximum power point.Simulation and test show that for partial shading, the improved algorithm can accurately and quickly search out the maximum power tracking point with 95% tracking accuracy, and searching efficiency is 28% higher than that of the traditional particle swarm algorithm.Especially, the local optimum can be avoided.

partial shade; maximum power point tracking; particle swarm algorithm; photovoltaic array

2014-09-01。 作者简介:胡克用(1978—),男,讲师;胥芳(通信作者),女,教授,博士生导师。 基金项目:国家“863计划”资助项目(2013AA050405);国家自然科学基金资助项目(51275470);教育部高等学校博士学科点专项科研基金资助项目(2013ZA11086)。

时间:2015-02-27

http:∥www.cnki.net/kcms/detail/61.1069.T.20150227.0846.012.html

10.7652/xjtuxb201504023

TK513.4

A

0253-987X(2015)04-0140-09