动理论在预测非阻塞性颗粒阻尼能量耗散中的应用

方江龙,王小鹏,陈天宁,张凯

(西安交通大学机械强度与振动国家重点实验室,710049,西安)



动理论在预测非阻塞性颗粒阻尼能量耗散中的应用

方江龙,王小鹏,陈天宁,张凯

(西安交通大学机械强度与振动国家重点实验室,710049,西安)

为了准确分析颗粒阻尼(NOPD)的能量耗散机理,拓宽颗粒阻尼在工程中的应用范围,根据分子动理论基本原理,建立非阻塞性颗粒阻尼能量耗散的定量模型。在振动流化床颗粒系统研究成果的基础上,认为当阻尼器内部的颗粒充分流化时,颗粒之间的物质输运和能量耗散由颗粒之间的碰撞主导;将阻尼器内部颗粒的运动与气体分子的运动进行类比,建立非阻塞性颗粒阻尼的能量守恒方程;通过求解颗粒系统的广义温度,得到非阻塞性颗粒阻尼能量耗散功率的定量模型。研究结果表明,颗粒阻尼的能量耗散功率随着颗粒直径的增大、颗粒层数的增多、材料密度的增加以及振动强度的提高逐渐提高。与现有模型相比,提出的模型颗粒阻尼的能量耗散功率不依赖颗粒内部速度梯度,因而具有更大的实际应用范围,也为更精确地描述非阻塞性颗粒阻尼的能量耗散机理提供了一种新的思路。

非阻塞性颗粒阻尼;动理论;能量耗散功率

非阻塞性颗粒阻尼(NOPD)又称粉体阻尼,是将金属或者非金属颗粒按一定的填充比填充到振动结构的空腔内,通过颗粒与颗粒之间以及颗粒与腔体壁之间的碰撞和摩擦耗能起到减振的作用。这一阻尼技术最早由文献[1]提出,经过几十年的发展,颗粒阻尼技术已被成功地应用于汽轮机叶片、捆钞机、齿轮机组、加筋板等不同结构中,起到了良好的减振效果。与传统的阻尼技术(如摩擦阻尼、黏弹性阻尼)相比,非阻塞性颗粒阻尼的特性基本不受外界环境的影响,因而在恶劣环境条件下仍具有良好的减振效果[2]。此外,非阻塞性颗粒阻尼具有减振频带宽、噪声小、对原始结构改变较小等优点,因而得到了人们的广泛关注。

对于NOPD,颗粒与颗粒之间以及颗粒与腔体之间的碰撞和摩擦是产生能量耗散的主要机理[3]。大量实验结果表明,颗粒阻尼的减振效果由结构的振动强度、颗粒的填充比、颗粒的大小以及颗粒材料密度等因素决定[4-5]。由于颗粒阻尼的能量耗散机理十分复杂,因而目前对颗粒阻尼减振效果的研究仍以实验分析和简单模型为主,如何确定颗粒的能量耗散功率与振动强度及颗粒参数的定量关系成为研究非阻塞性阻尼的关键和难点问题。

为了得到非阻塞性颗粒阻尼的能量耗散理论模型,常用的方法主要有离散元法、内蕴时间理论、两相流动理论以及湍流理论等。其中,文献[6]首次提出离散元法,经过不断的发展,目前已被广泛应用于采矿工程、岩土工程等。离散元法分析颗粒阻尼的减振机理时计算过程简单,且在颗粒数目较少的情况下有较好的精度,但其计算结果严重依赖颗粒的参数如恢复系数、摩擦系数等的选取[7],而且当颗粒数目较大时,计算效率低。文献[8]提出内蕴时间理论,用于描述耗散材料的黏塑性形变过程。文献[9]以内蕴时间理论为基础,结合NOPD的运动特性,首次得出了塑性应变与能量耗散之间的关系式。由于内蕴时间理论用于分析NOPD振动响应时需要做较多的简化和假设,故导致分析结果与实验结果存在较大的误差。文献[10]基于湍流的耗散统计模型,根据颗粒流类的流体性质,将颗粒的运动形态简化为充分发展的简单剪切流,得到了NOPD能量耗散率以及能谱密度的表达式。此外,吴成军教授首次将两相流理论用于建立非阻塞性颗粒阻尼的能量耗散[11],在充分发展的简单剪切流假设的基础上,得到了非阻塞性颗粒阻尼的等效阻尼系数,并成功预测了非阻塞阻尼悬臂梁结构的振动响应。湍流模型和两相流模型都将阻尼器内部颗粒的运动简化为简单剪切流,这与实际颗粒的运动状态有一定的差异。此外,两个模型所提出的等效阻尼系数和能量耗散率都包含速度梯度项,而颗粒内部的速度梯度一般很难直接获取,因而极大地限制了两个模型的实际应用。

本文在使用动理论对振动激励下的流化床进行研究的基础上[12],尝试将动理论的研究成果用于预测颗粒阻尼的能量耗散功率,得到了颗粒阻尼能量耗散功率与阻尼器相关参数如颗粒直径、颗粒密度、外界激励强度等的定量关系,并将得到的理论模型与现有的研究成果和实验现象进行对比验证,为建立非阻塞性颗粒阻尼能量耗散模型提供了一种新的思路。

1 动理论基本原理

对一个垂直激励的颗粒系统,随着颗粒层数的减少和激励强度的增加,颗粒的输运和能量的传递主要由颗粒之间的碰撞产生[13],文献[14]将碰撞主导的颗粒流系统与气体分子之间的碰撞进行类比。动理论表明,气体分子之间的碰撞可以描述为速度服从麦克斯韦分布的弹性颗粒在近似真空空间的自由运动。因而,如果将非阻塞性颗粒阻尼内部颗粒的运动状态与气体分子的运动进行类比,需满足以下基本条件[15]:颗粒之间的碰撞是颗粒输运和能量传递的主要机理;颗粒单次碰撞产生的能量损失与颗粒的动能相比较小;由摩擦产生的能量耗散与非弹性碰撞产生的能量损失相比较小。文献[15]表明,对于非阻塞性颗粒阻尼,当振动加速度较大时能量耗散主要由颗粒之间的非弹性碰撞产生。对于材料恢复系数接近1的颗粒,由单次碰撞产生的能量与颗粒动能相比自然较小。从而,将动理论用于预测非阻塞性颗粒阻尼能量耗散时应满足以下前提条件:颗粒的填充率较小;振动激励的加速度值较大;颗粒材料的恢复系数接近1。

1.1 颗粒系统的输运方程

对于一个充分流化振动的颗粒系统,类比气体分子动理论,定义颗粒的物理量,如颗粒的动量或者动能的统计平均值为[16]

(1)

式中:n为颗粒的粒子数密度,即单位体积内颗粒的个数;v为颗粒速度;f(1)(r,v,t)为颗粒的速度分布函数。对于单位体积dr内颗粒的物理量ψ的平均〈nψdr〉主要受到3个方面的影响:颗粒速度随时间的变化;颗粒在微元内的流入流出;微元内部颗粒的碰撞。借助流体力学输运方程的概念,可以建立颗粒系统的输入方程[16]如下所示

(2)

式中:Ai为外界作用力引起的ψ的变化;Af表示颗粒流入流出微元引起的ψ的变化;Ac表示微元内部颗粒互相碰撞引起的ψ的变化。Ai、Af、Ac的表达式如下所示[16]

(3)

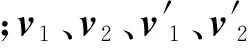
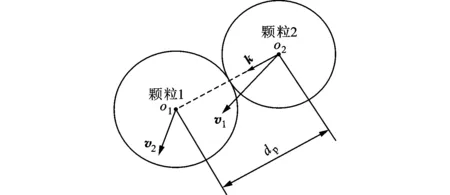
图1 颗粒二碰撞示意图

因而,Ac可以表示为如下形式[15]

Ac=-·θ+χ

(4)

(v12·k)f2(r-dk,v1;r,v2;t)dkdv1dv2

(5)

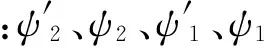
进而颗粒的输运方程可以表示为如下形式

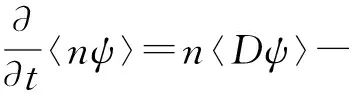
(6)

f2(r-dk,v1;v2;t)dkdv1dv2

(7)

1.2 速度分布函数

当颗粒系统内部的颗粒充分流化后,颗粒之间的能量耗散以及质量输运由颗粒之间的碰撞主导时,认为颗粒的速度分布服从麦克斯韦分布[17],满足如下形式

(8)

(9)

其中

式中:∂p为颗粒的填充率。

对于简单剪切流,如库特流以及颗粒在斜坡上向下流动时,颗粒单位体积的能量耗散功率可表示为[17]

(10)

2 非阻塞性颗粒阻尼的功率耗散模型

对于填充率不高的颗粒阻尼器,当受到的振动激励加速度较大时,颗粒进入类气态,能量耗散主要由颗粒之间的碰撞产生。在将分子动理论应用于剪切颗粒流和振动颗粒流研究的基础上,尝试使用分子动理论建立非阻塞性颗粒阻尼在进入类气态后的功率耗散模型。文献[12]指出,垂直激励下流化的颗粒速度分布满足麦克斯韦-玻尔兹曼分布,满足如下关系式

(11)

依据分子动理论的基本原理,只需要确定广义温度Tc,即可确定由颗粒碰撞产生的功率耗散。当碰撞为主要的能量耗散机理时,就可近似认为碰撞产生的能量耗散功率即为非阻塞性颗粒阻尼的能量耗散功率。

2.1 非阻塞性颗粒阻尼的能量流

当给非阻塞性颗粒阻尼施加一个振动激励时,由腔壁施加给内部颗粒的能量等于颗粒之间的耗散以及颗粒与腔壁之间的耗散[12],即满足如下关系式

Pb=Dpp+Dpw

(12)

式中:Pb为腔壁对颗粒的输入功率;Dpp为颗粒之间的耗散功率;Dpw为颗粒与腔体之间的耗散功率。

对于二维非阻塞性颗粒阻尼,当颗粒的速度分布满足式(11),不计颗粒摩擦时由碰撞产生的能量耗散满足如下关系[13]

Dpp=(π/2)1/2(1-e2)NmgH(Tc/m)1/2

(13)

式中:N为单位长度上颗粒的数目;g为重力加速度;H为颗粒的层数。当颗粒为非光滑颗粒时,考虑到颗粒的旋转引起的颗粒之间的能量交换,单次碰撞产生的能量耗散满足以下关系[18]

(14)

(15)

所以考虑颗粒的旋转动能后,单位长度上颗粒碰撞产生的能量耗散功率可以表示为

(16)

颗粒与腔壁侧面碰撞产生的能量损失为

(17)

式中:L为颗粒阻尼器的长度;Ex/E为颗粒在x方向的动能与颗粒总动能的比值,一般为小于0.2的常数;h、h0分别为颗粒在稳态和静止状态下颗粒等效中心的位置。

由以上分析可以得出,当非阻塞性颗粒阻尼的主要能量耗散机理为颗粒之间以及颗粒与腔壁之间的碰撞产生的能量损失时,单位长度上的能量耗散功率可以表示为

(18)

2.2 非阻塞性颗粒阻尼广义温度的确定

为确定颗粒阻尼的能量耗散功率,需要对其广义温度进行计算。根据2.1节对非阻塞性颗粒阻尼能量流的分析,非阻塞性颗粒阻尼的能量耗散功率等于阻尼器腔壁对颗粒阻尼输入的功率。

定义腔壁底面的振动速度为U,P(U)为表面速度的概率密度函数,则P(U)dU为壁面速度位于U～dU的概率。腔体表面向颗粒传递的功率可以表示为[19]

(19)

当腔体的振动为简谐激励时,经计算可得

(20)

式中:Umax=Aω为简谐振动激励的振动速度幅值。联立式(16)、式(17)、式(20),可得

(21)

进而得到广义温度

(22)

3 非阻塞颗粒阻尼的能量耗散功率及参数分析

得到非阻塞性颗粒阻尼的广义温度后,将式(22)代入式(18),可以得出单位长度上非阻塞性颗粒阻尼的能量耗散功率的表达式为

(23)

为了研究耗散功率随颗粒参数的变化,做出以下近似处理:对于非阻塞性颗粒阻尼,当腔体的尺寸确定,以及腔体内颗粒运动充分发展时,可以近似认为L、μ以及Ex/E均为常数,因而可以认为颗粒阻尼的能量耗散功率仅与颗粒材料的恢复系数e、颗粒直径dp、颗粒的层数H、颗粒的密度ρ,以及腔体的振动速度幅值Aω相关。

(24)

得到颗粒阻尼的能量耗散规律如图2～图5所示,其中图2参数e=0.92,ρ=7 800 kg/m3,A=0.002 m,ω=2π·100 rad/s;图3参数e=0.92,ρ=7 800 kg/m3,A=0.002 m,ω=2π·100 rad/s;图4参数e=0.92,H=15,A=0.002 m,ω=2π·100 rad/s;图5参数e=0.92,H=15,A=0.002 m,ρ=7 800 kg/m3。

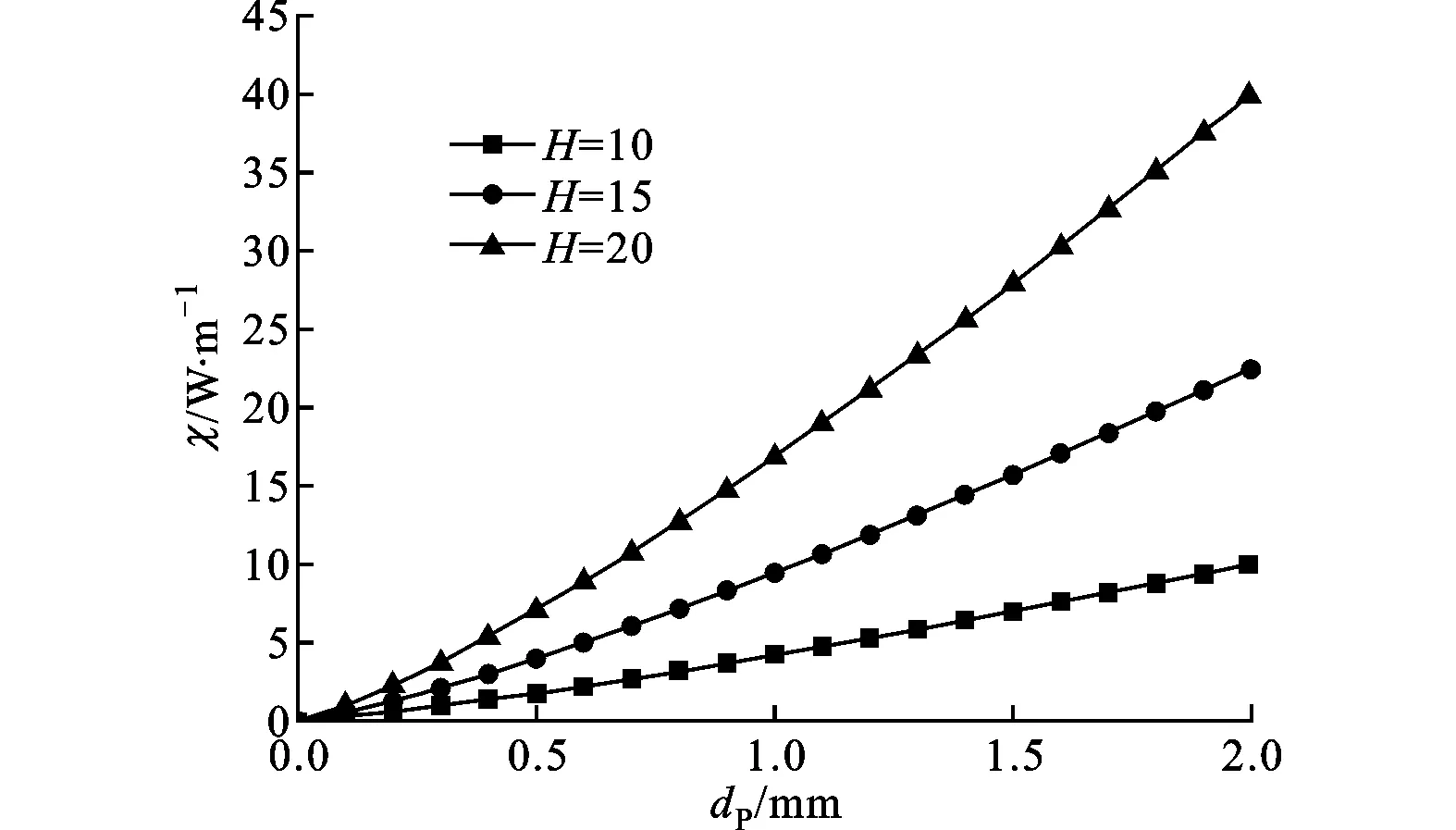
图2 不同颗粒层数时能量耗散功率随颗粒直径的变化

图3显示,随着颗粒层数的增加,非阻塞性颗粒阻尼的能量耗散功率逐渐增大。当非阻塞性颗粒阻尼器的空腔一定时,随着颗粒层数的增加,颗粒的填充率增大。因而,由以上模型可以得出,在一定范围内随着颗粒填充率的增加,非阻塞性颗粒阻尼的能量耗散功率逐渐增大,与文献[10]中的结论一致。

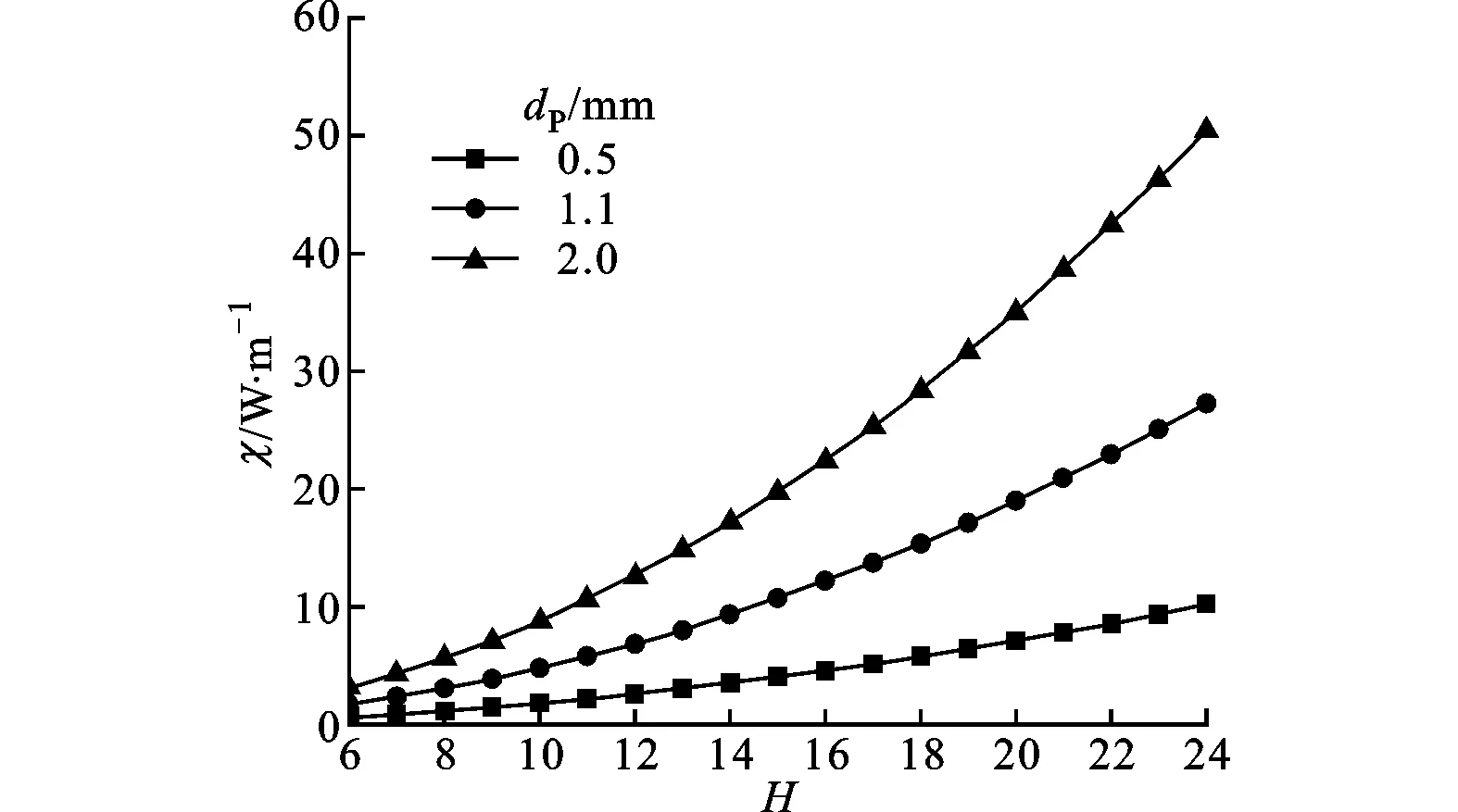
图3 不同颗粒直径时能量耗散功率随颗粒层数的变化

图4显示,由于耗散功率与ρ3/4成正比,因而随着颗粒密度的增加,非阻塞性颗粒阻尼的能量耗散功率逐渐增大。这一结论解释了使用非阻塞性颗粒阻尼时选取密度较大的材料具有更好的减振效果这一实验现象。

图4 不同颗粒直径时能量耗散功率随颗粒密度的变化

图5表明,随着振动速度的增加,颗粒阻尼的能量耗散功率逐渐增大。这是由于随着振动速度的增加,颗粒的广义温度升高,颗粒的运动更加剧烈,进而导致颗粒之间的碰撞次数和单次碰撞产生的能量损失增加。这一结论与结构振动强度较大时,非阻塞性颗粒阻尼有更好的减振效果这一实验现象一致。

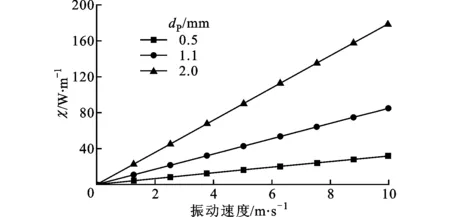
图5 不同颗粒直径时颗粒耗散功率随振动速度的变化

4 结 论

本文使用动理论来描述非阻塞性颗粒阻尼内部颗粒的运动状态,建立了非阻塞颗粒阻尼能量耗散功率的定量模型,得到了颗粒阻尼的能量耗散功率与颗粒参数以及振动强度的定量关系。分析结果表明,非阻塞颗粒阻尼的能量耗散功率随着颗粒直径的增大、颗粒层数的增加、颗粒密度的提高以及外界振动强度的增强而逐渐提高。这一结论与前人的实验和仿真结果有良好的一致性。

与现有模型相比,本文所提出的基于动理论的颗粒阻尼的能量耗散模型,能量耗散功率的大小取决于外界振动的强度而不是颗粒的速度梯度,从而具有更大的实用性。此外,由于本文所建立的模型能够确定外界振动强度及颗粒阻尼参数与能量耗散功率的定量关系,因而使得优化颗粒阻尼参数以实现在最少的颗粒下取得最好的减振效果成为可能。本文的研究结果对进一步研究颗粒阻尼的能量耗散机理以及颗粒阻尼的实际应用有一定的指导意义。

[1]PANOSSIAN H.Non-obstructive impact damping applications for cryogenic environments [C]∥Proceedings of Damping’89.West Palm Beach, Florida, USA:NTIS, 1989:1-9.

[2]BAI X M, SHAH B, KEER L M, et al.Particle dynamics simulations of a piston-based particle damper [J].Powder Technology, 2009, 189(1):115-125.

[3]BAI X M, KEER L M, WANG Q J, et al.Investigation of particle damping mechanism via particle dynamics simulations [J].Granular Matter, 2009, 11(6):417-429.

[4]PANOSSIAN H V.Structural damping enhancement via non-obstructive particle damping technique [J].Journal of Vibration and Acoustics, 1992, 114(1):101-105.

[5]PANOSSIAN H V, EHRGOTT R.Non-obstructive particle damping (NOPD) treatment optimization for composite honeycomb panels [C]∥Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.New York, USA:ASME, 2007:2047-2057.

[6]CUNDALL P A.A computer model for simulating progressive large scale movements in blocky rock systems [C]∥Proc Symp Rock Fracture (ISRM).Wroclaw, Poland:ISRM, 2013:1-8.

[7]张超, 陈天宁, 王小鹏, 等.颗粒阻尼线性离散元模型参数的选取方法 [J].西安交通大学学报, 2014, 48(3):96-101.ZHANG Chao, CHEN Tianning, WANG Xiaopeng, et al.Parameter selection method for linear discrete element modal of particle damper [J].Journal of Xi’an Jiaotong University, 2014, 48(3):96-101.

[8]VALANIS K C, FAN J.A numerical algorithm for endochronic plasticity and comparison with experiment [J].Computers & Structures, 1984, 19 (5):717-724.

[9]王炜, 黄协清, 陈天宁.基于内蕴时间理论极值特性的 NOPD 结构的响应仿真 [J].系统仿真学报, 2003, 15(6):849-851.WANG Wei, HUANG Xieqing, CHEN Tianning.Response simulation of non-obstructive particle damping structure based on extremal properties of endochronic theory [J].Journal of System Simulation, 2003, 15(6):849-851.

[10]崔致远, 吴九汇, 陈花玲, 等.基于统计方法的 NOPD 耗能机理定量分析 [J].振动与冲击, 2012, 31(9):135-139.CUI Zhiyuan, WU Jiuhui, CHEN Hualing, et al.Quantitative analysis on energy dissipation mechanism of non-obstructive particle damping technology [J].Journal of Vibration and Shock, 2012, 31(9):135-139.

[11]WU C J, LIAO W H, WANG M Y.Modeling of granular particle damping using multiphase flow theory of gas-particle [J].Journal of Vibration and Acoustics, 2004, 126(2):196-201.

[12]MCNAMARA S, LUDING S.Energy flows in vibrated granular media [J].Physical Review:E, 1998, 58(1):813-823.

[13]KUNAMARA V.Kinetic theory for a vibro-fluidized bed [J].Journal of Fluid Mechanics, 1998, 364:163-185.

[14]CULICK F E C.Boltzmann equation applied to a problem of two-phase flow [J].Physics of Fluids (1958-1988), 1964, 7(12):1898-1904.

[15]CHEPURNIY N.Kinetic theories for granular flow:inelastic particles in Couette flow and slightly inelastic particles in a general flow field [J].Journal of Fluid Mechanics, 1984, 140(222/223):223-256.

[16]SAVAGE S B, SAYED M.Stresses developed by dry cohesionless granular materials sheared in an annular shear cell [J].Journal of Fluid Mechanics, 1984, 142:391-430.

[17]JENKINS J T, SAVAGE S B.A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles [J].Journal of Fluid Mechanics, 1983, 130:187-202.

[18]MCNAMARA S, LUDING S.Energy nonequipartition in systems of inelastic, rough spheres [J].Physical Review:E, 1998, 58(2):2247-2251.

[19]MCNAMARA S, BARRAT J L.Energy flux into a fluidized granular medium at a vibrating wall [J].Physical Review:E, 1997, 55(6):7767-7771.

(编辑 杜秀杰)

Application of Kinetic Theory to Quantitative Analysis Model of Non-Obstructive Particle Damping

FANG Jianglong,WANG Xiaopeng,CHEN Tianning,ZHANG Kai

(State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

To investigate energy dissipation mechanism of non-obstructive particle damping (NOPD) accurately, the kinetic theory is employed to establish a quantitative analysis model.When the particles of NOPD are uniformly fluidized, the mass transport and energy exchange are dominated by the collisions among the particles.Solving the energy conservation equation of the NOPD, the temperature and the energy dissipation power of NOPD are obtained.The theoretical results show that NOPD energy dissipation power rises with the increasing particle diameter, layer number, material density and vibration amplitude.Compared with the previous analysis models of NOPD, the proposed model does not depend on the velocity gradient of particles, which widens the practical applications, and provides a new way to revealing energy dissipation mechanism of NOPD.

non-obstructive particle damping; kinetic theory; energy dissipation power

2014-08-18。 作者简介:方江龙(1990—),男,硕士生;王小鹏(通信作者),男,副教授。 基金项目:长江学者和创新团队发展计划资助项目(IRT1172)。

时间:2014-10-31

http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.014.html

10.7652/xjtuxb201504003

TH703.62

A

0253-987X(2015)04-0012-06