一种快速3D打印分层方向确定算法

罗楠,王泉,刘红霞

(西安电子科技大学计算机学院,710071,西安)



一种快速3D打印分层方向确定算法

罗楠,王泉,刘红霞

(西安电子科技大学计算机学院,710071,西安)

针对减少3D打印等分层制造应用中成型的模型实体与理论模型之间的体积偏差,提出一种快速精确的分层方向确定算法。通过分析体积偏差的产生原因和理论模型,明确了统一分层厚度下使体积偏差最小的分层方向,是与模型面片面积加权法向量内积绝对值之和最小的单位向量,将最优方向选取问题转化为最小绝对偏差线性回归问题。用最小二乘准则近似最小绝对偏差准则,并用基于该准则的主成分分析方法,对加权法向量的散列矩阵进行特征值分解,从特征向量中快速确定最优的分层方向。针对多个不同复杂程度的模型进行评估实验,结果表明,该算法能在保证精度的前提下将运算量减少80%,适合于复杂精细模型的分层制造应用。

3D打印;体积偏差;分层方向;线性回归;主成分分析

3D打印是快速成型技术[1]的一种,采用分层制造的思想,将三维模型沿分层方向离散为一组二维图形,即一组薄层(也被称为切片或者分层),逐层加工形成三维模型实体,这种技术已被引入到许多实际应用当中[2-3]。STL模型[4]作为为快速成型技术服务的文件格式,被3D打印技术采用,但STL数据无法直接作为3D打印的输入数据,必须通过分层软件转化为打印机可直接处理的数据形式。决定分层结果的因素有分层方向和分层厚度。分层厚度指相邻两个切片之间的纵向距离,分层方向即切片平面的法向量方向,分层厚度越小,构建的模型越细腻,构建时间也就越长。在分层厚度给定时,分层方向唯一决定模型构建的效果。由于分层厚度受打印机硬件条件限制,只能在一定范围内调整,需根据实际情况折中处理,因此本文只关注分层方向的确定。

影响分层方向的因素有多个,如表面精度、支撑体积、构建时间、总消耗等。其中表面精度指的是构建的模型实体与理论模型的接近程度,是衡量成型质量的最重要指标。支撑体积用来支撑模型中倾斜或悬空的部分,保证成型的顺利进行。对于结构简单的部件,用户一般可以根据经验选择与某坐标轴平行的方向作为分层方向,但对于面片众多、结构复杂的模型则难以判断,必须根据一定标准确定最优的分层方向。现有算法一般选取单个或多个因素构造目标函数,然后从候选方向中选择使目标函数值最小的方向作为最优分层方向。单目标算法[5-9]以最主要的单一因素如体积偏差或表面平整度为目标函数,可以得到单一目标下的最优方向。多目标算法[10-13]选取多个因素如表面精度、构建时间、材料消耗等作为优化目标确定折中的分层方向,每个目标所占比重根据经验确定。在候选方向预定义方面,一般由用户根据经验指定若干方向,或对方向空间进行采样获取一定数量候选方向,或使用模型表面面片法向量等几何特征作为候选方向。这些方法基本都是基于遍历枚举思想,需对候选方向逐个计算目标函数,复杂度高,只适用于几何特征简单的规则模型,对于由大量三角面片组成的复杂模型,往往时间效率不能满足要求,并且由于预定义的方向是有限的,总会有一定机率错过最好的方向。因此,寻找一种快速精确的分层方向确定算法尤其必要。

本文以最少体积偏差为目标,提出一种快速分层方向确定算法。通过分析体积偏差的产生原因和数学模型,明确模型面片面积对体积偏差的影响,指出在统一分层厚度下,最优分层方向是与面积加权法向量内积绝对值之和最小的单位向量,并将问题进一步转化为最小绝对偏差线性回归问题;使用最小二乘准则替代最小绝对偏差准则,借助主成分分析和矩阵分解相关理论技术,近似估计线性回归参数,快速确定最优分层方向。算法无需预定义初始候选方向,而是根据模型本身的特征自适应获得最优分层方向,避免了遍历候选方向带来的计算量,很大程度上提高了时间效率,而且保持了很好的模型构建精度。

1 体积偏差

在3D打印或者其他快速成型技术中,模型的体积偏差定义为构建模型使用的材料与理论模型需要的材料之间的差值。体积偏差主要影响模型的构建精度,体积偏差越小,构建的模型表面与理论模型表面越接近,模型实体的表面精度就会越高。分层处理时在模型表面上产生的阶梯效应[14]是引起模型误差体积的直接原因。

1.1 误差分析

3D打印采用的是分层制造的原理,在进行构建时,打印机并不会制造出与理论模型完全相同的面片,而是通过分层切割的方式用一系列阶梯面近似表达每个面片(类似楼梯)。如图1所示,使用统一的分层厚度l对表面Fi进行分层,图中灰色块ΔV代表相邻两个分层在该表面上产生的阶梯效应,称作误差体积。理论上来说,分层厚度越小,制造的表面越接近理论表面,误差体积越小,模型构建就越精确,但由于设备精度的限制,分层厚度只能取有限值,在分层厚度确定的情况下,分层方向唯一决定误差体积的大小。

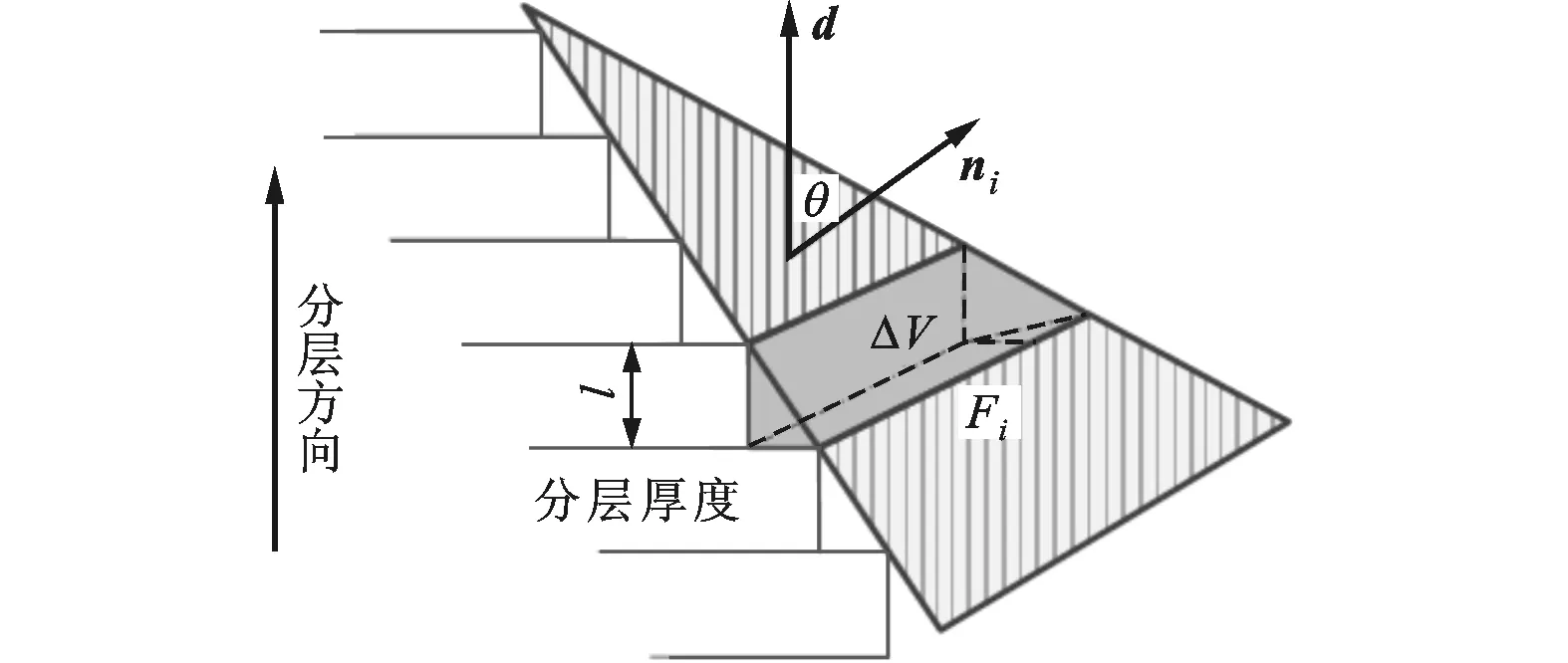
(a)面片Fi分层情况

(b)侧面剖视图图1 分层时的阶梯效应

图1b为面片Fi分层情况的侧面剖视图,图中虚线即表面的理论侧视线,阶梯实线表示实际的分层效果,灰色小三角代表分层时产生的局部体积偏差,右图为放大效果。图中d为分层方向单位向量,ni为三角形面片Fi的单位法向量,l表示分层厚度,θi为ni与d之间的夹角,ΔF表示误差块在面片Fi上所占面积,ci为面ΔF上的高,即

ci=l|cosθi|;cosθi=d·ni

(1)

误差块ΔV的体积

ΔV=(1/2)ciΔF

(2)

面片Fi分层时所产生的体积偏差

Vi=∑ΔV=(1/2)ciFi

(3)

式中Fi也代表该面片的面积。整个模型分层产生的误差体积

(4)

令Ni=Fini为表面Fi的面积加权法向量,此时误差体积表示为

(5)

从式(5)可以看出,体积偏差与分层厚度l成线性关系,l越小,则对应的体积偏差也越小。在l给定的情况下,V取决于分层方向与面片加权法向量Ni内积绝对值之和,而每个面片的面积加权法向量Ni在模型给定时即已确定,所以体积偏差就取决于分层方向。

因此,要获得最小的分层误差体积,只须确定一个分层方向,使得该方向与所有加权法向量的内积绝对值之和最小即可。

1.2 数学模型

由于分层方向为单位向量,其与加权法向量的内积绝对值即为加权法向量到分层方向上的投影长度值,因此上述问题可另述为:已知模型的加权法向量集Nn={N1,N2,…,Nn},求单位向量d,使得Nn中所有向量到d的投影长度之和最小。

图2为加权法量在分层方向的投影示意图,为方便观察理解,只画出了几个向量,其余的向量只标出了终点位置。从图中可看到,法向量Ni到方向d的投影长度为ξi。

图2 加权法向量到分层方向投影

记d=(a,b,c)T,Ni=(xi,yi,zi),Nn到d的投影长度之和为L,则有

(6)

结合式(5)可知,L取最小值时体积偏差V最小。

考虑线性回归模型

yi=xiβ+εi,i=1,…,n

(7)

式中:(xi,yi)为第i个观测数据;β为回归系数向量;εi为未观测到的误差。对于所有观测数据,使得总体拟合误差最小

(8)

可见分层方向的确定只取决于加权法向量的分布情况。已知加权法向量分布,与法向量内积绝对值之和最小的分层方向确定问题,等价于一个最小绝对偏差的线性回归问题。

2 解决方案

2.1 最小二乘近似

在线性回归领域,最小绝对偏差方法(LAD)和最小二乘方法(LS)常被用来进行回归模型的统计分析。两种方法的误差分析准则为

(9)

与LS方法不同,LAD方法只考虑残差的一次方,故其所受异常点的影响小很多,能产生更为稳健的参数估计。然而,LAD方法并无解析最优解,为线性规划问题,使用迭代方法求解,在样本数量较大时,计算量很大,从而限制了该方法的应用和发展。相比LAD,LS方法包含完善的理论推理和方差分析方法,且存在唯一解析最优解,计算简单、高效。

因此,本文使用最小二乘准则替代最小绝对偏差准则,进行线性回归参数的近似估计。借助主成分分析(PCA)[16]和矩阵特征分解的相关理论和技术,可以非常快速地求出线性回归参数,即分层方向。虽然使用最小平方准则会产生一些误差,但算法的效率得到了很大的提升。

2.2 分层方向确定

PCA是统计学中一种通过减少数据集维度来简化分析的技术。PCA的基本思想是从最小平方角度寻找一个最能代表数据的投影。

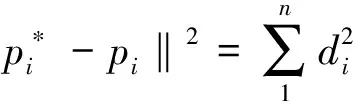
(10)

(11)

通过对矩阵A进行特征分解,可得两个特征值λ1、λ2(λ1>λ2),以及对应的两个特征向量e1、e2。e=e1时J达到最小值;e=e2时J达到最大值。

图3 PCA方法的最小平方解释

由图3可知

(12)

将该结论扩展到三维欧式空间,如图4所示。对于一个封闭三角网格模型来说,其中所有三角形的面积加权法向量之和为0,即加权法向量终点的均值位于坐标系原点o。对加权法向量集Nn应用PCA可求得一条过原点o的直线,使得所有法向量在该直线的投影平方和最小,该直线所在的方向即法向量散列矩阵的最小特征值对应的特征向量e3。

图4 加权法向量集PCA示意图

算法主要步骤如下。

(1)读取STL模型M,计算M每个三角面片法向量;

(2)计算M每个三角面片面积,并根据面积依次更改法向量长度,得到加权法向量集Nn;

(3)依公式(11)计算Nn的散列矩阵A;

(4)对矩阵A进行特征值分解,得到3个特征向量e1、e2、e3;

(5)分别以e1、e2、e3为分层方向计算误差体积,取其中最小误差体积的方向作为最终分层方向。

由于面积加权法向量的均值位于坐标系原点,计算A时,可以使用更简单的公式

(13)

省去计算均值的步骤。对矩阵A进行特征值分解,会得到3个特征值λ1、λ2、λ3(λ1>λ2>λ3)及对应的3个特征向量e1、e2、e3,按照采用的近似准则及PCA理论分析,应取向量e3作为分层方向。然而由于近似时存在的误差,对于某些模型,以e3作为分层方向的结果略逊于e1或e2时的结果。因此,在算法实施时,需通过计算从3个特征向量中选择最优的一个作为最终确定的分层方向,以保证算法的精度。

3 实验结果

将本文的高效自适应分层方向确定算法与两种常用算法进行了比较,分别是法向量遍历算法和方向空间全局搜索算法[5],实验中且称为算法1和算法2。法向量遍历算法使用模型中所有三角面片的法向量作为候选方向,空间采样算法从方向空间中采样一定数量的候选方向(实验中取方向数m=18×18),而后对每个候选方向计算体积偏差,选择最优方向。为了便于理解和比较,效仿空间采样算法借助球坐标系,使用方位角(φ,θ),φ,θ∈[0°,180°)表示分层方向,如图5所示。

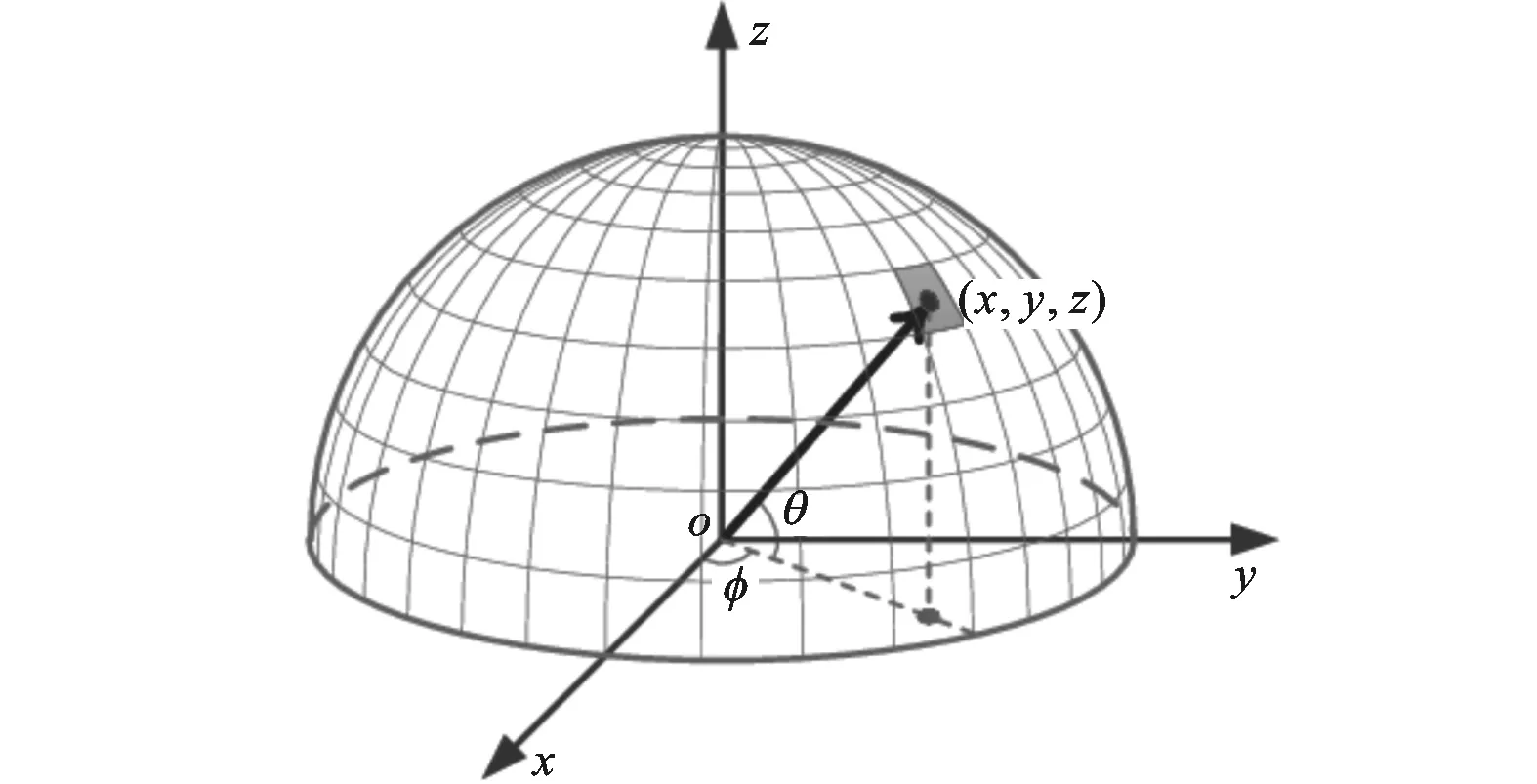
图5 分层方向球坐标表示

实验从效率和精度两个角度评估算法。3种算法应用于10个不同复杂程度的STL模型,比较确定的分层方向、体积偏差和运行时间。STL模型如图6所示,从上到下从左到右依次编号为1～10,其所包含的三角面个数见表1。实验平台为Windows7,运行机器为I3双核CPU,主频为3.3 GHz,内存2 GB,运行环境为VisualStudio2010,算法实现语言为C++。

表1列出了分层厚度为0.01 mm时3种算法针对10个模型得出的分层方向、体积偏差以及运算时间,由于模型尺寸大小不一,不同模型体积偏差的数值相差较大。

算法1 遍历模型中所有三角面的法向量,计算每个法向量对应的体积偏差,每次体积偏差的计算都要对所有加权法向量进行内积运算,计算复杂度为logN2;算法2对每个采样方向都进行一次体积偏差的计算,计算速度取决于采样数m和模型复杂程度,时间复杂度为mlogN;本文算法只需对模型的加权法向量集的散列矩阵进行一次特征值分解,计算效率只取决于模型的三角面片个数,时间复杂度为logN。

图6 10个STL模型

模型编号名称面片数分层方向(ϕ，θ)/(°)算法1算法2本算法体积偏差/mm3算法1算法2本算法计算时间/s算法1算法2本算法1CupCake861(90，0)(50，0)(146，0)65833065156365189510170032Bottle1240(0，96)(0，90)(0，90)39007638642538642720240043Bunny15110(1，73)(0，100)(0，90)0．257740．237740．23968270970174MakeRobot11966(90，90)(90，90)(90，88)1004111004111020241352250425MyScan23826(92，91)(90，10)(114，39)2239822062762149246114570856Bunny269630(1，98)(0，100)(0，90)010243700992821010032556×10313402487Buddha99448(0，43)(80，90)(90，90)071969206571380663926112×10319023548Trya200000(165，9)(70，170)(90，0)0．4675190．4522010．453515439×10337927009Armadillo212539(176，177)(90，110)(90，90)0．7449310．6393430．650632503×103402175410Angel270285(0，90)(0，90)(174，92)340710340818343179768×1035136978

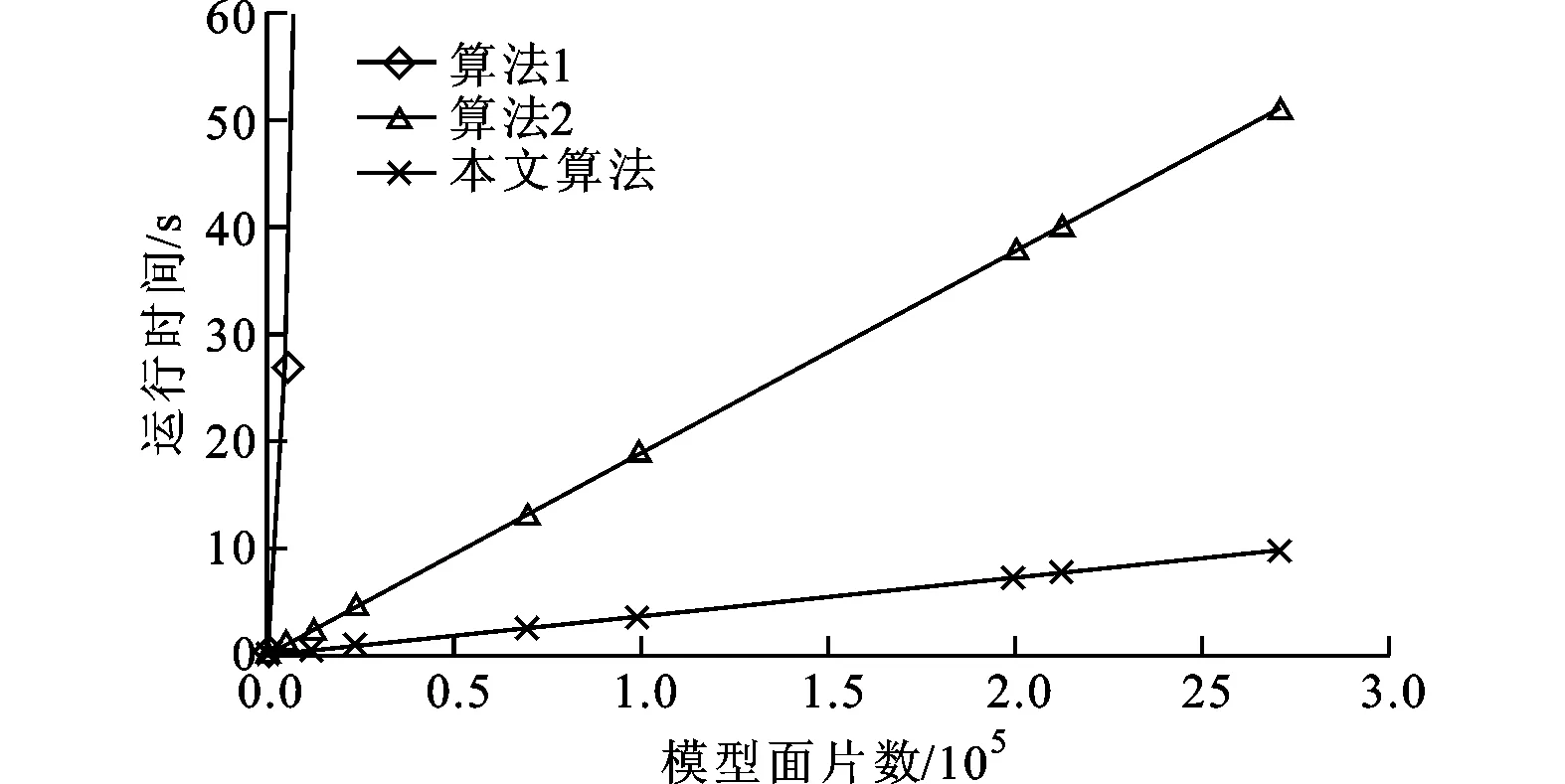
图7 3种算法运行时间

图7为3种算法的时间曲线,符合时间复杂度分析。由于坐标范围的限制,算法1只展示了部分曲线。由图7可以看出,本文算法在运算效率上优势明显,耗时大幅减少,仅不到算法2的20%。对于简单的STL模型,只需几十至几百毫秒,对于面片数在2×105的模型只需7 s左右,对最复杂的模型计算时间也在10 s之内,具有很强的适用性。相比而言,算法1适用于简单模型,对于复杂模型,尤其是面片数在5 000以上的STL模型,时间复杂度急剧增加,难以应用。算法2有效降低了时间复杂度,但是该方法受限于采样数。若采样数目小,速度会更快,却很有可能错失更优方向;若数目太大,计算效率势必受影响。实验中取m=324,对面片数目在5×104以下的模型,可在10 s之内得到最优分层方向,对于更复杂的模型,则需要更长的用户等待时间。

(a)与算法1相比

(b)与算法2相比图8 本算法与算法1、2的精度性能比较

图8给出了本文算法与对比算法在精度提升方面的比较,此处精度指的是算法在减少体积偏差方面的能力。相比法算法1,本文算法平均可减少3.6%的体积偏差,对模型3、7、9甚至超过了7%,但针对模型4、10也出现了微小的反复。与算法2相比,本文算法在精度方面平均降低1.16%,但除了个别模型(模型5),下降的幅度均很小,平均只有0.7%。该结果完全在可接受范围内,也与2.1节中的叙述吻合,虽然精度略微下降,但计算效率大幅提升。综合来看,本文提出的分层方向确定算法高效、可行。

4 结 语

本文以减小3D打印中的体积偏差为目标,提出了一种快速的分层方向确定算法。文中分析了分层时体积偏差的产生原理,指出模型面片面积对体积偏差的重要影响,引入面积加权法向量的概念,提出了一种新的体积偏差计算模型。基于该模型将最优分层方向确定问题转化为最小绝对偏差线性回归问题,并使用最小二乘准则近似最小绝对偏差准则,借助主成分分析方法快速求解分层方向。

该算法摒弃了遍历查找的思想,避免预定义候选方向,而是根据模型特征自适应地确定最佳分层方向。算法能在兼顾分层精度的同时,快速求得最优分层方向,相比已有算法展现出较大优势,使用简单、效率高,适合复杂精细模型的3D打印等分层制造应用。

[1] CHUA C K, LEONG K F, LIM C S. Rapid prototyping: principles and applications [M]. Singapore: World Scientific, 2010: 1-23.

[2] NOVAK J, NOVAKOVA L, BARNA J, et al. Application of FDM rapid prototyping technology in experimental gearbox development process [J]. Tehniki vjesnik-Technical Gazette, 2012, 19(3): 689-694.

[3] 王烨, 贺健康, 刘亚雄, 等. 三维微流道支架直接压印成形方法 [J]. 西安交通大学学报, 2012, 46(10): 116-120. WANG Ye, HE Jiankang, LIU Yaxiong, et al. Direct imprinting of three-dimensional microfluidic scaffolds [J]. Journal of Xi’an Jiaotong University, 2012, 46(10): 116-120.

[4] 3D Systems. Stereolithography interface specification [M]. Rock Hill, South Carolina, USA: 3D Systems, 1988.

[5] AHARI H, KHAJEPOUR A, BEDI S. Optimization of slicing direction in laminated tooling for volume deviation reduction [J]. Assembly Automation, 2013, 33(2): 139-148.

[6] AHN D, KIM H, LEE S. Surface roughness prediction using measured data and interpolation in layered manufacturing [J]. Journal of Materials Processing Technology, 2009, 209(2): 664-671.

[7] PAUL B K, VOORAKARNAM V. Effect of layer thickness and orientation angle on surface roughness in laminated object manufacturing [J]. Journal of Manufacturing Processes, 2001, 3(2): 94-101.

[8] LIN F, SUN W, YAN Y. Optimization with minimum process error for layered manufacturing fabrication [J]. Rapid Prototyping Journal, 2001, 7(2): 73-82.

[9] PHAM D, DIMOV S, GAULT R. Part orientation in stereolithography [J]. The International Journal of Advanced Manufacturing Technology, 1999, 15(9): 674-682.

[10]VIJAY P, DANAIAH P, RAJESH K. Critical parameters effecting the rapid prototyping surface finish [J]. Journal of Mechanical Engineering and Automation, 2011, 1(1): 17-20.

[11]CANELLIDIS V, GIANNATSIS J, DEDOUSSIS V. Genetic-algorithm-based multi-objective optimization of the build orientation in stereolithography [J]. The

International Journal of Advanced Manufacturing Technology, 2009, 45(7/8): 714-730.

[12]BYUN H S, LEE K H. Determination of the optimal build direction for different rapid prototyping processes using multi-criterion decision making [J]. Robotics and Computer-Integrated Manufacturing, 2006, 22(1): 69-80.

[13]THRIMURTHULU K, PANDEY P M, REDDY N V. Optimum part deposition orientation in fused deposition modeling [J]. International Journal of Machine Tools & Manufacture, 2004, 44(6): 585-594.

[14]DOLENC A, KEL M I. Slicing procedures for layered manufacturing techniques [J]. Computer-Aided Design, 1994, 26(2): 119-126.

[15]CHEN K, YING Z L, ZHANG H, et al. Analysis of least absolute deviation [J]. Biometrika, 2008, 95(1): 107-122.

[16]SHLENS J. A tutorial on principal component analysis [EB/OL]. [2014-09-28]. http:∥arxiv.org/pdf/1404.1100.pdf.

(编辑 赵炜)

A Fast Determination Algorithm for Slicing Direction of 3D Printing

LUO Nan, WANG Quan, LIU Hongxia

(School of Computer, Xidian University, Xi’an 710071, China)

An efficient determination algorithm on slicing direction is proposed to reduce the volume deviation between fabrication entity and its theoretical model in layered manufacturing applications such as 3D printing. The cause of volume deviation and its mathematical model are analyzed, and the results show that the optimal slicing direction with the least volume deviation is a unit vector with the minimum value in the sum of absolute inner products of the vector and the area weighted normal vector of model facets. Thus, the problem to determine the optimal direction is converted into a linear regression problem with the least absolute deviation. The least absolute deviation norm is approximated by using the least squares norm and the principal component analysis method is used to process eigenvalue decomposition on the scatter matrix of weighted normal vecter. The optimal direction is then efficiently determined from the eigenvectors. Experiments on several models with different complexity show that the proposed algorithm reduces 80% of the computation load on the premise of guarantee accuracy, and is suitable for layered manufacturing of complex models.

3D printing; volume deviation; slicing direction; linear regression; principal component analysis

2014-11-03。

罗楠(1987—),男,博士生;王泉(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61070045)。

时间:2015-03-03

10.7652/xjtuxb201505022

TP391

A

0253-987X(2015)05-0140-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150303.1110.004.html