众里寻他千百度定位不准难觅处——“物体位置的确定”教学实录及其思考

☉江苏省无锡市雪浪中学 戴倍琪

☉江南大学附属实验中学 庞彦福

·江苏省无锡市庞彦福名师工作室·

众里寻他千百度定位不准难觅处
——“物体位置的确定”教学实录及其思考

☉江苏省无锡市雪浪中学 戴倍琪

☉江南大学附属实验中学 庞彦福

一、对教材理解及教学观点

若给你一张无锡大剧院的入场券，根据入场券的排号和座号，你能够确定应该入场的位置吗？

人们在生活、生产实践中常常需要确定物体的位置，如影剧院里的座位，棋盘上棋子的位置，城市地图上车站、学校、医院、风景区的位置，在海洋中确定船只或舰艇的位置，以及战争中要打击的目标的位置……

在生活中，确定物体的位置有哪些方法呢？怎样描述你在教室里的座位呢？需要几个数据呢？

大千世界的各种变化可以用数量来描述，物体的位置往往可以由数据来刻画，数量的变化与位置的变化有着密切的联系．在现实生活中往往需要确定物体的位置，因此研究物体位置的确定就成了学科及领域需要学习的内容．

从《课标》来看，关于“物体位置的确定”在小学阶段已经有所了解，第一学段（1～3年级）的要求是“会用上、下、左、右、前、后描述物体的相对位置；给定东、南、西、北四个方向中的一个方向，能辨认其余三个方向，知道东北、西北、东南、西南四个方向，会用这些词语描绘物体所在的方向”．第二学段（4～6年级）的要求是“能根据物体相对于参照点的方向和距离确定其位置；会描述简单的路线图；在具体情境中，能在方格纸上用数对（限于正整数）表示位置，知道数对与方格纸上点的对应”．进入初中之后，要求能“结合实例进一步体会用有序数对可以表示物体的位置”．对这一内容的了解和研究是为顺理成章地引入“平面直角坐标系”做铺垫，并且为进一步研究函数的有关内容奠定基础．本节课的教学通过实践、观察、记录、描图等活动，感受现实世界中事物之间的联系．在确定物体位置的过程中，进一步发展空间观念．

通过图形位置变化过程中相关数量的变化的讨论，引导学生经历发现问题、提出问题、分析问题和解决问题的过程．俗话说，良好的开始是成功的一半，初中阶段学习研究一次函数（包括正比例函数）、反比例函数、二次函数的图形与性质等，离不开平面直角坐标系，而“物体位置的确定”的学习则为“平面直角坐标系”的“登场”搭建了支架和平台．

本节课在已有知识及经验的基础上，理解确定位置的重要性和必要性，能够了解、掌握确定位置的方法，这是本节课教学的重点．

用方向角确定物体的位置时容易忽略掉“距离”这一要素，这应是教学的难点，同时确定物体的位置的方法是多种多样的，因此要灵活运用不同的方法确定物体的位置，在经历问题分析和解决的过程中，体悟其中所蕴含的数学思想，既是教学的重点，也是教学的难点．

二、课堂教学实录与说明

1.创设情境，感知确定位置的必要性

师：班主任老师利用星期天要去位于郊区的小明家（小明家住的是独门独户的房子，如图1）进行家访，你能给老师指路吗？

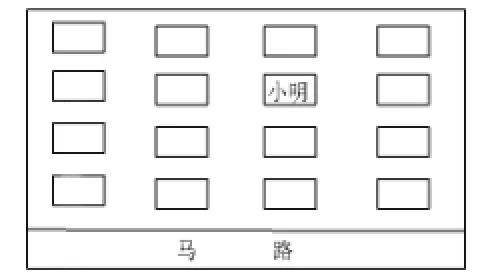
图1

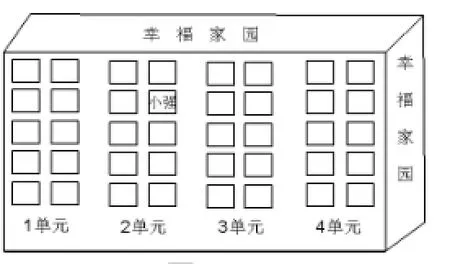
图2

生1：沿马路走，在马路左侧，第三排第三户便是．

师：如图2，住在幸福家园的小强家（城镇的商品房）老师也要去，你能给指路吗？该怎么找到呢？

生2：2单元四楼的一户．

生3：是2单元404室．

师：谢谢同学们热心而清晰的指路．老师一定能找到这两个同学家的位置．今天我们就来探究“物体位置的确定”．

说明：初中阶段认识、研究“定位”比小学里认识“定位”上了一个较大的台阶，小学阶段的第一学段主要是定性描述物体的位置，第二学段则过渡到用有序自然数对定量刻画物体的位置，现阶段是用有序实数对定量刻画点的位置及“定位”的方法和蕴含的坐标思想．生活中处处存在着数学，以实际问题作为引例，比较贴近学生的生活实际和学生的生活经验，显得自然，体现了生活中确定位置的重要性和必要性，本节课是研究物体（点）位置的确定，引入做到了开门见山，提出问题，为课堂探究做好了铺垫．教学是用教材教而不是教教材，创设情境、引入新课，选取素材可以是教科书中的，也可以根据学生情况、根据本地生活实际和学生的生活经验合理选用非教材中的适宜素材来引入新课．接近学生生活的情境能够使他们感受到学习数学的实际意义和实用性．备课要做到理解教材、理解学生、理解教学，并依据学生的认知起点实施教学．教学设计需要进一步优化和提炼，切实做到所选择的引入情境或素材要紧密联系教学内容，结合学生生活实际及认知基础，能够揭示数学本质．

2.探究体验，寻找确定位置的方法

师：如果将班级学生的座位约定从前往后为第一排、第二排、……依此类推，从进门往里为第一列、第二列、……依此类推，并且排在前、列在后，用（排数，列数）表示一个同学的座位位置，譬如小桐的座位可表示为（2，4）．请同学们报出自己当前的位置．

……

师：刚才是用有序数对来确定物体或点的位置．结合图3，你能向别人介绍或描述自己学校所在的位置吗？

生4：在人民医院的东侧．

图3

生5：别人要是不知道人民医院的位置呢？应该说成是在长安路与解放路交叉口的东侧解放路路南．

师：这样指就很清楚了，即使对这里的地形不熟悉，只要找到路标就能找到我们学校了．这种确定位置的方法是……？

生6：和地理课上利用经线纬线是同样的道理．

生7：这种方法也可以看作是找两线的交点．

师：很好的想法，善于知识的迁移与类比，是学习数学的好方法．

师：请同学们看图4，表示的是某次海战中敌我双方舰艇对峙示意图．对我方潜艇来说，北偏东40°的方向上有哪些目标？

图4

生8：有敌方战舰B和小岛．

师：距我方潜艇图上的距离1.5cm处的敌舰有哪几艘？

众生：用刻度尺测量，纷纷举手……

师：根据现有条件，你能确定每艘敌舰的位置吗？

生9：只能确定它们的方向，不能确定每艘敌舰的具体位置．

生10：要确定每艘敌舰的位置，还需要一个数据，就是距离．

师：方向角加上距离，你能说的更明白吗些？比如小岛距离我方舰艇90km，怎样描述小岛的位置？

生10：小岛在我方舰艇北偏东40°的90km处．

师：的确，利用方向角加上距离也能确定出物体或点的位置．

说明：随着学习内容的增加与深入，定位（确定位置）的方式方法丰富多样了，通过师生对话，交流讨论，进一步感受确定物体位置的几种常用方法，体会确定物体或点的位置方法的比较与合理选择．发展学生的数学应用意识．

3.拓展延伸，由确定物体位置到确定点的位置

师：如图5，点A在沿直线l自上而下运动的过程中，∠BAC的大小是如何变化的？

生11：先由小变大，再由大变小．

师：∠BAC变化的过程中，有最大值吗？

生12：∠BAC的最大值是180°，即点A运动到线段BC上时.

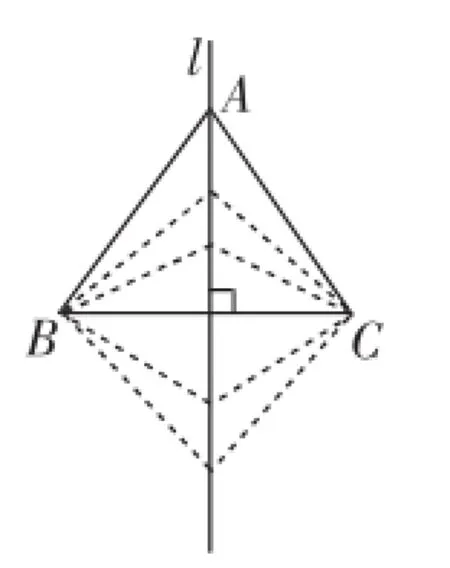
图5

师：∠BAC由小或变大的过程中，有最小值吗？生11：是接近0°，即无穷小的意思．

师：点A在什么位置时，△ABC是等边三角形？

师：你是怎么得出这个结果的？

生14：当△ABC是等边三角形时，可以根据勾股定理求得．

师：点A在什么位置时，△ABC是直角三角形呢？

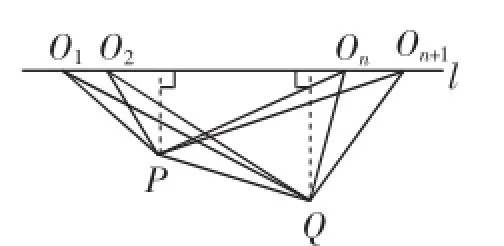
图6

师：如图6，当点O沿直线l从左向右运动时，△On+1PQ的周长是如何变化的呢？

生16：先变小再变大．

生17：点O从O1运动到O2的过程中，相应三角形的周长不断变小，点O从On运动到On+1的过程中，相应三角形的周长不断变大．

生18：△On+1PQ的周长先从无穷大逐渐变小，然后又逐渐变大．

师：在点O变化的过程中，形成的三角形的周长有没有最大值呢？

生18：没有．

师：有没有最小值呢？

生19：有．根据对称，作点P关于直线l的对称点P′，连接P′Q，P′Q与直线l的交点处即是周长最小的三角形顶点O的位置．

说明：学生随着年龄的增长，认知水平在提高，认识“定位”问题自然就上了台阶，从确定物体的位置过渡到确定点的位置，这是研究对象的数学化程度提高的象征．确定物体位置的方法是学习“图形与坐标”、“函数与图像”、“曲线与方程”的理论基础．随着学习的深入，用代数方法研究几何问题的步骤是：确定坐标原点→选择坐标系→用坐标（或方程）表示点（或曲线）→通过坐标（或方程）获得图形（或曲线）的几何信息，其蕴含的数学思想就是笛卡尔的坐标思想．研究思路是根据已有定位经验，概括定位方法，进而解决定位问题．体现了“具体→抽象→具体”的思维方法．通过教学能使学生明确用有序数组表示点的意义，理解掌握确定物体（点）位置的方法能够满足数学地解决生活中的定位问题的需要，体现了数学的育人意义及价值．其蕴含的形象思维及抽象思想、数形结合思想、对应思想等对发展学生智力和数学素养有着积极的影响．教学中，探索的思路让学生寻找，解决问题的方法让学生发现．引导学生观察、思考的过程，是为了让学生体会数与形的内在联系，增强学生“发现问题和提出问题、分析问题和解决问题”的能力．

4.总结回顾，反思提升

师：本节课我们研究的对象是什么？

生20：是物体或点．

师：研究的内容是什么？我们是怎样研究的？

生21：是确定这些物体或点的方法．……

师：常用确定物体位置的方法有哪些？如何简捷地表示物体的位置？

……

师：确定位置的过程中蕴含着哪些数学思想？

……

师：用有序数组表示点有何意义？

……

5.布置作业，巩固提高

必做与选做（略）.

三、教学思考与感悟

教师是课堂活动的设计者、引领者、参与者与合作者．教师的作用是唤醒学生求知、引导学生学习．有效的课堂活动需要老师给学生搭建平台，有了平台学生才便于表演；实现课堂教学有效性需要老师给学生寻找支点，有了合适的支点学生才会跳得更高．教师教学要根据学生已有的学习基础及生活经验，找准教学的逻辑起点，优化设计过程，合理实施课堂教学．教学中，注重对数学本质的认识和理解，提高学生认识数学、理解数学、应用数学的能力．数学教学的核心任务是培养学生的思维．探究性教学要根据学生的实际情况，通过合理的、适宜的问题，让学生经历直观、猜测、推理、发散、归纳、类比、概括、优化、反思等活动过程，感悟数学知识的形成过程及应用，加深理解数学知识与方法，养成良好的数学思维习惯，使学生的思维品质得到进一步提高．知识是能力的基础，能力是知识的升华，思想方法是其灵魂，解决问题是知识的运用，是获得能力的途径．在教学过程中要注重思想方法的渗透与提炼，只有这样，才能挖掘学生发现问题和提出问题的能力，才能发展学生分析问题和解决问题的能力．数学教学不能只让学生记住枯燥的结论，数学学习除了知识本身外，还要关注获得知识的过程，以及呈现数学知识载体的丰富内涵，防止让学生“只见树木不见森林”的现象．建造高楼必须打好基础，夯实楼基，数学学习同样要找准认知的起点，使知识在构建过程中形成体系，使学生在认知过程中理解数学．通过确定物体的位置到探究确定点的位置，进而为学习平面直角坐标系深入研究函数埋下伏笔，使研究内容由浅入深，层层递进．

1．中华人民共和国教育部制定．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

2．余文森，刘冬岩.有效教学的基本策略［M］.福州：福建教育出版社，2013．

3．杨裕前，董林伟．义务教育教科书·数学（七年级下册）［M］.南京：江苏科技出版社，2013．

4．庞彦福．初中数学有效教学［M］．北京：北京师范大学出版社，2015．

5．庞彦福，肖健，黄海涛.建立模型找关系抽丝剥茧现本质［J］．中学数学（下），2014（10）．

6．庞彦福，詹慧，翁寿峰．数学教师的“六研究”［J］．中学数学（下），2014（3）．H