基于微分平坦的滑翔式再入轨迹优化设计*
刘 莉,杨乐平,蔡伟伟,庄传刚
(1 国防科技大学航天科学与工程学院,长沙 410043;2 空间物理重点实验室,北京 100076)
基于微分平坦的滑翔式再入轨迹优化设计*
刘莉1,2,杨乐平1,蔡伟伟1,庄传刚2
(1国防科技大学航天科学与工程学院,长沙410043;2空间物理重点实验室,北京100076)
摘要:为优化设计多约束条件下高超声速再入轨迹,研究了一种基于微分平坦理论的数值方法。引入独立伪控制输入及其始终为零的附加约束,扩展系统的微分平坦属性,将初始优化问题转换到平坦输出空间中,避免积分运算的同时降低了设计维度;采用样条插值参数化平坦输出,将平坦输出优化问题转化为非线性规划问题求解。仿真表明:该方法能够较快的设计出满足约束的再入轨迹,具有一定的工程参考价值。
关键词:高超声速滑翔;轨迹优化;微分平坦;样条插值
0引言
高超声速再入滑翔过程中,飞行器面临严峻的气动热、动压和过载等约束,优化设计满足各类约束的飞行轨迹是其应用的关键技术之一,也是当前研究的热点问题[1-3]。然而,约束复杂、积分运算、决策变量过多等因素极大限制了此类优化问题的求解效率。近年来,一种基于微分平坦理论的轨迹优化方法因其在减少计算量、提高求解效率方面效果显著而引起广泛关注[4-5]。该方法从系统的微分平坦属性着手,构建系统状态和控制变量与平坦输出间的映射关系,将问题转换为平坦输出的优化问题,避免积分运算的同时降低了系统设计的维度。
文中针对高超声速滑翔飞行器轨迹优化问题,引入伪控制输入及其始终为零的附加约束,扩展了再入运动模型的平坦属性,使之适用于基于微分平坦的轨迹优化方法;采用样条插值函数参数化平坦输出,将平坦输出优化问题转换为非线性规划问题,求解得到优化的滑翔式再入轨迹。
1再入轨迹优化问题描述
1.1 运动模型
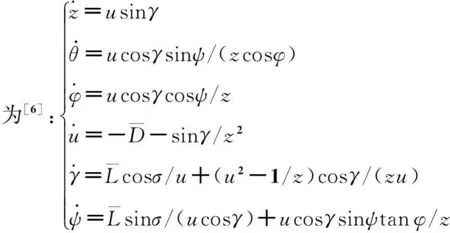
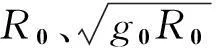

(4)
1.2 约束条件
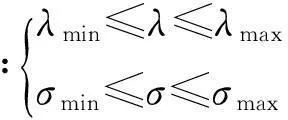
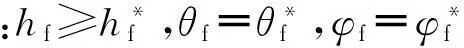
(7)
1.3 性能指标
性能指标可以依据飞行任务及轨迹规划目的的不同合理选择。飞行器再入过程中经历恶劣的气动热环境,为降低防热系统重量,提高有效载荷比重,可选择驻点热流峰值最小或总加热量最小为性能指标。对到达指定目标点类任务,飞行时间也是一类重要的性能指标。
2再入轨迹优化方法
2.1 微分平坦方法
(8)式中:x∈Rn为状态变量;u∈Rm为控制输入,f为连续光滑函数。若存在一组输出y∈Rm满足:
yi=hi(x,u,…,u(ri)),(i=1,…,m)
(9)
且系统状态和输入能够表示为:
(10)
则称该系统是微分平坦的,并记y为平坦输出,ri(i=1,…,m)为yi的相对阶。
平坦系统的状态和输入与平坦输出间存在可逆映射关系,即系统运动行为能够完全由平坦输出决定。因此可以将初始的轨迹优化问题映射到平坦输出空间中,通过优化平坦输出进而设计出系统期望的状态和输入。基于微分平坦的轨迹优化方法具有下列优势:1)利用平坦输出及其有限阶导数表示系统状态和输入,可以消除微分动力学约束;2)由于平坦输出与控制输入维数相等,对于具有高维状态空间的系统,该方法能够减少系统分析设计的维数,降低问题求解难度。
2.2 再入运动模型微分平坦属性
研究表明再入运动三自由度运动模型不具备微分平坦属性[7],无法直接基于微分平坦开展轨迹设计。因此,首先引入伪控制输入及其附加约束,扩展系统的平坦属性。在再入运动模型中引入独立于λ和σ的伪控制输入T:
(11)
以无量纲地心距z、经度θ和纬度φ为平坦输出,分别记为ζ1=z,ζ2=θ,ζ3=φ,则其余状态变量可表示为:
(12)

式(12)对无量纲时间τ求导得:
(13)

将式(2)、式(4)、式(12)和式(13)代入式(1)中得到泛化升力系数关于平坦输出及其导数的表达式:
(14)
将式(12)~式(14)代入式(1)得到倾侧角表达式:
(15)
(16)
综上,伪控制输入T的引进扩展了系统的微分平坦属性,使得再入运动的状态和输入均可表示成平坦输出及其导数的函数,从而将初始优化问题映射到平坦输出空间中求解。为确保伪控制输入引入前后优化问题的等价性,要求T始终为零,即:
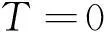
(17)
2.3 平坦输出优化
本节对平坦输出进行离散化处理,将平坦输出优化问题转换为非线性规划问题,应用合适的非线性优化算法求解得到平坦输出解。
将无量纲时间区间τ∈[τ0,τf]转换到κ∈[0,1]上:
(18)
则平坦输出对无量纲时间τ的导数满足:
(19)
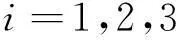
采用区间κ∈[0,1]上均匀分布的N个离散点对平坦输出进行离散,并以这些离散点为节点插值逼近平坦输出。考虑到平坦输出与系统状态和输入间的映射关系涉及到平坦输出的一阶和二阶导数信息,选用分段三次样条插值函数来逼近平坦输出,以确保插值点处平坦输出二次连续可微。通过对插值函数求导近似平坦输出的导数,最终将问题转换为以插值点上的平坦输出值为决策变量的非线性规划问题。采用序列二次规划算法进行求解得到期望的平坦输出轨迹,代入相关表达式中即可得到滑翔式再入最优轨迹及其控制量。
3仿真分析

以在[0,1]上均匀分布的30个点为插值点,利用三次样条插值函数逼近平坦输出,则转换所得的非线性规划问题包含91个决策变量。选取[0,1]上等距分布的40个点为配点,要求优化轨迹在配点处满足所有路径约束。为降低优化求解的难度,设置伪控制输入引起的附加约束容忍度为5×10-3,优化得到的飞行时间为1 693 s。

表1 再入飞行任务描述

图1 平坦输出曲线
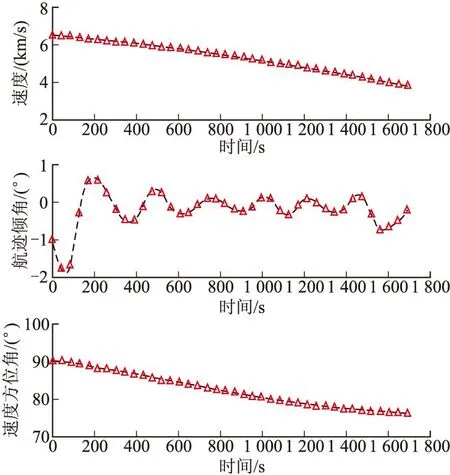
图2 其余状态变量曲线
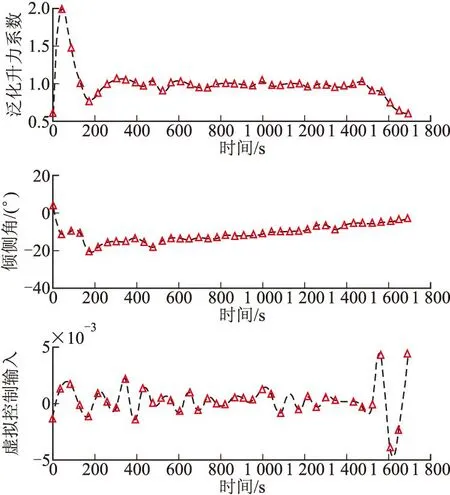
图3 控制输入曲线
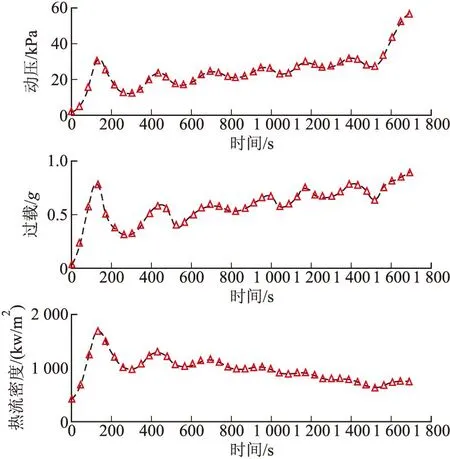
图4 路径约束曲线
4结论
文中基于微分平坦理论研究了高超声速再入滑翔飞行器轨迹优化问题,根据理论分析和数值仿真得到如下结论:
1)伪控制输入及其附加约束的引入使得再入运动模型形式上呈平坦系统,适用于基于微分平坦的轨迹优化方法,扩展了微分平坦方法的应用范围;
2)利用系统状态和控制变量与平坦输出及其导数间的可逆映射关系可以将轨迹优化问题映射到平坦输出空间中,降低系统设计的维度并消除动力学微分约束,提高求解效率;
3)数值仿真表明所研究的方法能够较快的优化得到满足各类约束的一般再入轨迹,其对于大转弯之类的特殊情况的适用性有待进一步研究。
参考文献:
[1]周浩, 周韬, 陈万春, 等. 高超声速滑翔飞行器引入段弹道优化 [J]. 宇航学报, 2006, 27(5): 970-973.
[2]陈小庆, 侯中喜, 刘建霞. 高超声速滑翔式飞行器再入轨迹多目标多约束优化 [J]. 国防科技大学学报, 2009, 31(6): 77-83.
[3]Rahimi A, Kumar K D, Alighanbari H. Particle swarm optimization applied to spacecraft reentry trajectory [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 307-310.
[4]Louembet C, Deaconu G. Collision avoidance in low thrust rendezvous guidance using flatness and positive B-splines [C]∥American Control Conference, San Francisco, USA, June 29-July 01, 2011.
[5]Chamseddine A, Zhang Y M, Rabbath C A, et al. Flatness-based trajectory planning/replanning for a quadrotor unmanned aerial vehicle [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 2832-2848.
[6]赵汉元. 飞行器再入动力学与制导 [M]. 长沙: 国防科技大学出版社, 1997.
[7]Neckel T, Talbot C, Petit N. Collocation and inversion for a reentry optimal control problem [C]∥Proceedings of the 5th International Conference on Launch Technology, 2003.
收稿日期:2014-03-10
作者简介:刘莉(1973-),女,吉林松原人,高级工程师,硕士,研究方向:临近空间飞行器指挥控制及在线任务规划。
中图分类号:V448.2
文献标志码:A
Differential Flatness Based Trajectory Optimization for Glide-reentry
LIU Li1,2,YANG Leping1,CAI Weiwei1,ZHUANG Chuangang2
(1College of Aerospace Science and Engineering, National University of Defence Technology, Changsha 410043, China;
2Science and Technology on Space Physics Laboratory, Beijing 100076, China)
Abstract:Concentrating on trajectory optimization problem of hypersonic reentry under multi-constraints, a differential flatness based numerical approach was studied. By introducing the concept of pseudo input and its additional zero value constraint, flatness of the reentry model was extended. Thus, the original optimization problem was mapped into flat output space, avoiding integral computation and reducing design dimension. The flat output optimization problem was ultimately transformed into a nonlinear programming problem by parameterizing the flat outputs with cubic spline functions. Numerical simulations indicate that the approach presented can generate trajectories that observe multi-constraints rapidly, and have some illumination for engineering application.
Keywords:hypersonic glide; trajectory optimization; differential flatness; spline interpolation

