大长细比飞行器整弹颤振性能分析*

杨亚东,冯　谦,王　栋,许　昌,侯小平

(北京航天微系统研究所,北京　100094)

大长细比飞行器整弹颤振性能分析*

杨亚东,冯谦,王栋,许昌,侯小平

(北京航天微系统研究所,北京100094)

摘要:大长细比飞行器弹体对升力面非定常气动力存在干扰,在超音速阶段,不应忽略该干扰对整弹颤振性能的影响。文中利用核函数法计算升力面的非定常气动力,比较了单升力面、升力面与弹体、整弹情况下的广义气动力,结果表明,存在干扰体时,非定常气动力出现很明显的变化。在此基础上进行的全弹颤振计算表明,弹体干扰在非定常气动力和全弹颤振计算中不可忽略,弹体的干扰提高了整弹颤振临界速度。

关键词:气动弹性;颤振;大长细比;干扰

0引言

颤振是飞行器设计与分析中极为重要的气动弹性动稳定性问题,对非定常气动力的计算是颤振计算的重要工作之一。舵片、弹翼和弹身组合布局型式的飞行器各部件间存在复杂的气动干扰,如升力面之间的气动力干扰、弹身对升力面的影响、气流经过升力面后的阻滞作用、舵片尾涡对弹翼的下洗等[1]。工程中往往对颤振计算模型进行大量简化,更多地关注升力面的颤振,只考虑孤立部件,忽略干扰,这可能带来一些问题。

大长细比导弹弹体本身的弯曲刚度相对较小,低阶模态表现为弹体弯曲振动,故考虑大长细比弹体影响的飞行器整体颤振成了设计中必须考虑的问题。升力面与弹身或是升力面之间的耦合非定常气动力的研究较少,史晓明等、刘超峰等利用当地流活塞理论计算了翼身融合导弹的颤振计算,只研究了超音速或高超音速弹体与升力面的耦合关系,缺少针对亚音速或是低超音速的情况[2-3]。

文中利用核函数法计算升力面的非定常气动力,采用细长体理论计算弹体上的气动力,通过干扰因子法考虑两者之间的干扰[1],研究了弹体对升力面非定常气动力的影响,不同飞行速度下弹体干扰特点,以及升力面之间的影响,考核了整弹的颤振临界速度。

1飞行器整体颤振方程

基于有限元方法[4],广义结构运动方程可以表示为如下的二阶常微分方程:

(1)

(2)

式中:w(x,y,z,t)表示飞行器表面的结构变形;q(t)为广义位移矢量;M、D和K分别是结构的广义质量、阻尼和刚度矩阵;QA为广义气动力矢量。

1.1　升力面气动力计算

升力面的非定常气动力计算基于偶极子网格法[5]。对于亚音速情况下,每个网格的无量纲下洗速度为:

(3)

式中Dij称为下洗影响系数。

超音速偶极子网格法与亚音速偶极子网格法基本相同。超音速下,每个网格的无量纲下洗速度为:

(4)

写成矩阵形式,可统一表达为:

(5)

求解式(5)可得载荷系数P,然后求出非定常气动力。

1.2　弹身气动力计算

采用细长体理论计算弹身的气动力,细长体理论有相当简单的解,计算量小,在弹身的颤振气动力计算中得到广泛的应用[6]。

图1　弹身的柱坐标系

根据图1所示的坐标系,可得单位长度上横向力分布:

Δp(x,t)=

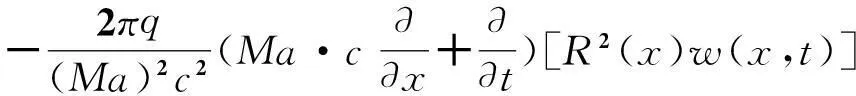
(6)

设弹身轴线振动挠度表示为z=z(x,t),当地来流速度v=Ma·c时,弹身表面x点的下洗为:

(7)

将式(7)代入式(6)可得单位长度振动气动力:

(8)

将式(8)进行广义化处理,可得弹身的广义气动力矢量:

(9)

式中Ab、Bb和Cb分别为广义气动力系数矩阵。

1.3　全弹组合体的非定常气动力干扰

利用干扰因子法进行求解。干扰因子法是以细长体理论为基础,只考虑弹身干扰对整个升力面的平均效应,忽略翼面上各点干扰影响的差异[7],使问题简化。

图2　全弹外形图

将如图2所示的串置翼布局的导弹,包括一对舵片和一对弹翼,考虑弹身干扰的升力面广义气动力矢量为:

(10)

式中,Bs0、BsH、Cs0、CsH分别为弹身对升力面干扰的广义气动力系数。

对于前升力面对后升力面的下洗问题,在非定常的涡系模型处理和定常流一样,将前升力面视为一附着涡面,进行工程简化,忽略附着涡和脱体涡对后升力面的影响,只考虑前升力面向后拖出的自由涡面或由它卷成的大漩涡的作用,可得后升力面的下洗附加气动力矢量:

(11)

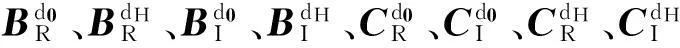
2影响分析

以某型导弹为例,文中分析了仅考虑升力面及考虑升力面和弹体干扰情况下的非定常气动力计算情况。该弹长细比为22,舵片和弹翼为前、后升力面,呈“××”型布局,见图2。由于弹体的长细比很大,一阶和二阶模态振型表现为弹体的弯曲振动。

2.1　弹体对升力面的影响

1)升力面在弹体头部

只考虑舵片所受的非定常气动力与舵片受到弹身干扰的气动力进行比较见图3,选取展长30%处,缩减频率k=0.12时,Ma=0.5和Ma=1.5两个速度进行计算。图3绘出非定常气动力升力系数沿弦向的变化曲线。在亚音速下,考虑弹身干扰的情况下,舵片前缘所受非定常气动力比不受干扰时高114%,而后缘非定常气动力都趋于零。在超音速下,考虑弹身干扰的情况下,在后缘处,弹体是否存在干扰对非定常气动力的影响很大,其压力系数实部绝对值相比为41%,不受弹体干扰时虚部压力系数趋于零,说明在超音速阶段不考虑弹体的气动干扰得到的气动面所受非定常气动力误差会很大。

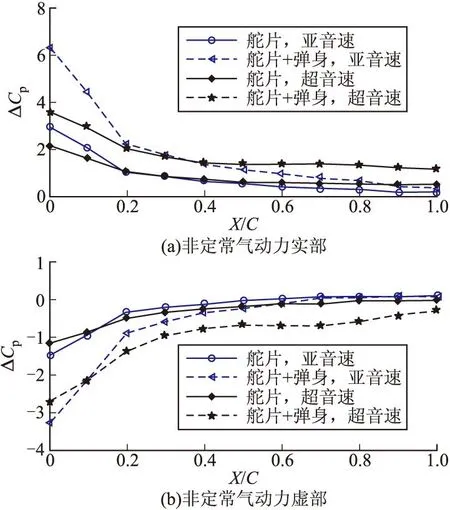
图3　舵片所受非定常气动力

2)升力面在弹体尾部

分析弹翼与分析舵片的过程类似,从图4可以看出亚音速下,翼面前缘所受的非定常气动力的虚部,在弹身干扰下比无弹身干扰高达118%,实部比无弹身干扰时高近126%,而后缘的非定常气动力趋近零,弹身干扰对后缘干扰不明显;在超音速情况下,弹身干扰作用更加明显,弹身干扰对弹翼弦向各位置非定常气动力的影响大致平稳。

图4　弹翼所受非定常气动力

3)升力面分布弹体两端

图5将整个升力面作为考察对象,绘出后升力面的非定常气动系数。亚音速下,弹身干扰对弹翼前缘非定常气动力实部的影响达176%,对前缘非定常气动力虚部的影响达117%,从前缘往后缘,干扰的影响逐渐减小,至趋于零。超音速下,弹身干扰对弹翼弦向各位置非定常气动力实部和虚部的影响大致平稳。可见,弹体干扰明显改变了整个弹翼的非定常气动力的大小和分布。

图5　弹翼所受非定常气动力

2.2　升力面之间的影响

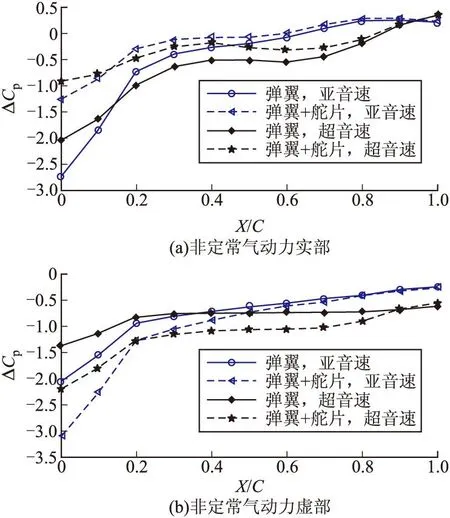
图6　弹翼所受非定常气动力

舵片对弹翼的干扰与弹翼自身气动力的比较见图6,计算非定常气动力时未考虑弹身的影响。图中给出了在舵片干扰下,弹翼沿弦向所受的气动力分布曲线,从图中可以看出弹翼前缘部分受舵片的影响较大,存在干扰比没有舵片干扰下的气动系数实部绝对值在亚音速下小近51%,在超音速下小近54%,而虚部在亚音速下大51%,在超音速下大60%;而在后缘处前升力面对气动力影响较小,都趋于零。

2.3　整弹颤振影响

将一阶广义非定常气动力虚部绘制如图7,可以看出亚音速的广义气动力绝对值比超音速大,弹体干扰时气动力绝对值比无干扰时大。从图8可以看出由于弹体的干扰影响,无论在亚音速或是在超音速下,整弹颤振临界速度有所增加。

图7　不同减缩下一阶广义气动力虚部比较图

图8　整弹颤振曲线

3结论

大长细比导弹发生颤振的机理和单独升力面的情况有所不同,需要区别对待,文中通过实例计算分析得到:

1)在计算细长体导弹舵片和弹翼上的非定常气动力时,有必要考虑弹身对升力面的非定常气动力干扰,这种干扰是不能忽略的。

2)前升力面对后升力面也会产生影响,这种影响改变后升力面非定常气动力的大小,从而改变整弹的颤振临界速度。

3)如果整弹发生颤振,则弹体的干扰将提高整弹颤振临界速度。

参考文献:

[1]管德. 飞机气动弹性力学手册 [M]. 北京: 航空工业出版社, 1994.

[2]刘超峰, 李海东, 杨炳渊, 等. 身-翼-舵组合体高超声速变攻角颤振计算 [J]. 宇航学报, 2011, 21(8): 1663-1668.

[3]史晓明, 杨炳渊, 李海东, 等. 基于当地流活塞理论的翼身组合体飞行器大攻角超声速颤振分析 [J]. 空气动力学学报, 2012, 30(5): 664-667.

[4]陈桂彬, 邹丛青, 杨超. 气动弹性设计基础 [M]. 北京: 北京航空航天大学出版社, 2004.

[5]管德. 非定常空气动力计算 [M]. 北京: 北京航空航天大学出版社, 1991.

[6]赵永辉. 气动弹性力学与控制 [M]. 北京: 科学出版社, 2007.

[7]杨炳渊. 颤振的工程计算方法: 防空导弹结构与强度 [M]. 北京: 宇航出版社, 1993.

收稿日期:2014-01-08

作者简介:杨亚东(1984-),男,河南人,硕士研究生,研究方向:飞行器强度设计,气动弹性。

中图分类号:V215.3

文献标志码:A

Flutter Performance of the Whole Missile with Large Fineness Ratio

YANG Yadong,FENG Qian,WANG Dong,XU Chang,HOU Xiaoping

(Beijing Aerospace Microsystems Institute, Beijing 100094, China)

Abstract:The interfere of body to lift face could not ignored in the influence of the flutter performance of the whole missile with large fineness ratio. The unsteady aerodynamic of lift face was computed using kernel function method, and unsteady lift coefficient was compared between only lift face and lift face with interfere of the body, then the general aerodynamics of whole missile was computed in the modal coordinates; it was found that difference was obvious. The flutter of the whole missile indicates that the interfere of body can not ignored in calculating the unsteady aerodynamics and the flutter of the whole missile, the interfere of body improves the flutter critical velocity of the whole missile.

Keywords:aeroelastic; flutter; large fineness ratio; interfere