基于图谱的交互电网临界点搜索算法

2015-12-25 05:35刘春

上海电力大学学报 2015年4期

基于图谱的交互电网临界点搜索算法

刘春

(上海电力学院电气工程学院, 上海200090)

摘要:构建了符合当前交互电网实际的模型及连锁故障机制,并提出了一种基于图谱的算法来搜索对网络安全影响最大的临界点,对这些临界点加以重点保护可以有效地提高网络鲁棒性.该算法以代数连通性来评估故障后网络连通性,不需要搜索最大连通分量,仿真结果证明其在执行效率和速度方面有较为明显的优势.

关键词：交互电网; 图谱; 代数连通性; 临界点

收稿日期：2014-09-24

作者简介：通讯刘春(1982-),女,硕士,讲师,湖北孝感人.主要研究方向为电力系统信息化处理.E-mail:liuchun@shiep.edu.cn.

中图分类号：TM711;TM715文献标志码： A

收稿日期：2014-09-24

作者简介：通讯高亮(1960-),男,教授,山西太原人.主要研究方向为电力系统继电保护、智能化变电站技术.

ResearchonCriticalPointSearchAlgorithmofInteractiveGridBasedonMapSpectrum

LIUChun

(School of Electrical Engineering,Shanghai University of Electric Power, Shanghai200090, China)

Abstract:The topology of interdependent power grid is modeled,with more real world characters taken into account,as well as the propagating mechanism of cascading failures.An efficient algorithm is also proposed based on Graph Spectrum Theory,for detecting the critical nodes of interdependent power grid,which is the first step of protection.In this approach,the robustness of leftover power grid after cascading failure is evaluated in the metric of algebraic connectivity,instead of giant connected component,whose searching procedure takes much running time.The experimental results highlight the advantage of this approach in speed.

Keywords:interdependentpowergrid;graphspectrum;algebraicconnectivity;criticalnodes

随着信息科学的发展,越来越多的大型人造网络倾向于彼此耦合、信息交互,典型的例子有电力网、社交网络、交通网络与通信网的交互.这种交互固然提高了这些大型人造网络的智能化水平,但也存在一些不可忽视的负面效应.已有的研究结果表明，在面对随机攻击和蓄意攻击时，交互网络比单个网络表现得更加脆弱,因此近年来引起了广泛的关注.文献[1]至文献[7]对交互网络和单个网络的鲁棒性均有涉及,得出的共同结论是交互网络比单个网络更加脆弱.这是因为在发生连锁故障时,故障并不仅仅在单个耦合网络中传播,还通过这两个网络的交互引起反馈效应,使得故障影响的范围更广.文献[3]从渗流的角度分析了交互性对于网络相变的影响,结果表明,在单个网络中发生的是连续的二阶相变,而在交互网络中发生的是不连续的一阶相变,这对网络的保护十分不利.文献[4]进一步指出,要使得交互网络的相变由一阶退化为二阶,应减小两个网络间的耦合程度.文献[1]和文献[5]分别对交互网络在面对随机和蓄意攻击时的鲁棒性进行了分析,认为交互网络在两种攻击下都会比单个网络显得更脆弱.上述文献都是基于通用的网络模型,并无特别针对某种实际的网络,得出的结论也较有一般性；通常采用无标度模型来建模,用于评估脆弱度或者鲁棒性的参数也基本为度、中心度等通用的参数,不带有具体网络的特征，因此应用到具体的网络中时,与实际情况存在一定的差距.文献[6]针对的是电网和通信网组成的交互网络,提出了在交互电网中确定临界节点的两种算法.所谓的临界节点指的是其失效会对整个网络造成最大损失的节点.很显然，在网络的设计阶段就应该对于这些临界节点予以重点保护.文献[7]仍然采用的是无标度网络模型,但是电网和通信网所取的幂律分布指数β分别在2.5~4和2.2~2.6之间,符合实际电网和Internet网络的特性.

确定临界节点是提高网络鲁棒性的第一步,本文的设计目标也在此.但是对于在此过程中如何计算网络的损失,本文采用了不同的角度.一般认为，网络的损失是丢失了最多的连通节点,因此在计算网络损失时必须统计故障后网络剩余最大连通分量的长度，这就需要复杂的搜索算法,在网络规模较大时尤为困难.本文采用了代数连通性来取代最大连通分量长度去衡量剩余网络的鲁棒性，代数连通性已被证明可以直接反应网络的拓扑特性,而且计算复杂度低于搜索最大连通分量.仿真结果表明，该方法可以提高算法的效率.

1代数连通性

设有无向图G(V,E)有N个顶点,顶点集为V,边集为E,邻接矩阵为A.节点i的度表示为deg(i),将所有节点的度写成一个对角阵D,则称D为G的度矩阵.图G的拉普拉斯矩阵L(G)定义为:

(1)

也可写成:

(2)

可见L为半正定对称阵,因此其所有特征值非负.L的所有特征值的集合即称为图G的拉普拉斯谱.将L的所有特征值按从小到大的顺序排列为0=λ1(G)≤λ2(G)≤λ3(G)…≤λN(G),其中λ2(G)称为图G的代数连通性,该特征值对应的特征向量定义为费德勒向量(FieldVector).[9]

代数连通性λ2(G)也称为谱隙(SpectralGap),反应了网络中节点连接的紧密程度.当λ2(G)→0时网络趋于不连通,而当ελ2(G)→1时网络趋于全连通.这里的ε是与网络规模相关的正则化常数.著名的Courant-Fisher定理给出了λ2(G)的解法为:

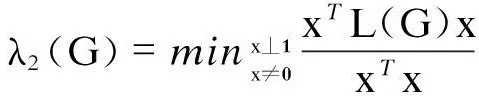
(3)

式(3)中0=(0,0,…,0)T和1=(1,1,…,1)T为λ1(G)=0对应的特征值.[10]

图1给出了两个节点数和度分布完全相同的图,但是直观可以看出图1a比图1b的连接要弱.计算得出这两个图的代数连通性分别为0.438 4和1.000 0,与直观观察的结果相符.这是一个简单的例子,现有文献已经证明代数连通性不仅直接反映系统的鲁棒性,还与一些重要的图变量有关,[10-14]在此不再赘述.此外,代数连通性的计算可归结为特征值求解或二次规划问题,求解相对容易,尤其是在网络规模较大时,其速度优势更为明显.

图1　代数连通性与鲁棒性的关系

(4)

2网络模型

为了更接近实际的电力网与通信网,本文电力网的模型采用IEEE-BUS系统,通信网仍采用Internet网络常用的无标度模型.

根据文献[3]和文献[4]的结论,交互网络的耦合不应太强,但耦合阈值的大小并无定论.此外,遵循两个网络节点的度正相关的策略进行耦合可以提高鲁棒性.因此,本文采用的耦合策略是部分耦合,首先计算两个网络中各节点的度并进行排序,然后取度排序前50%的节点按排序产生一条耦合边.这里的耦合边在物理上对应信息流和供电线路,也就是说,电力网中的节点通过耦合边从通信节点获取信息,同时向通信节点供电,当电力节点失效时,通信节点必然失效,反之则不然.这样的设置符合当前的实际情况.

在上述策略下生成交互网络Γ(Gs,Gc,Esc),其中，Gs为电力网，Gs=(Vs,Es);Gc为通信网，Gc=(Vc,Ec);Esc为二者的耦合边,即Esc={(u,v)|u∈Vs,v∈Vc}(其中u和v分别为Gs和Gc中的节点).

在连锁故障机制方面,大部分文献是假设交互网络中的某一个网络在节点失效时,与之相连的本网节点以及耦合节点均失效.而实际电网及耦合通信网络中的情况与此不同.连锁故障首先是由电网中的节点失效引起的,但电网中节点失效的直接后果是全网的潮流重新分配,并不一定导致其邻居节点失效.参照电网连锁故障的经典CASCADE模型的做法并不失一般性,本文假设Gs中某个节点失效的条件是其邻居节点中失效的比例超过某一个阈值,Gc中节点失效的条件是其邻居节点失效或耦合节点失效.

3GS-AN算法

建立交互网络Γ(Gs,Gc,Esc)后,寻找其临界点的问题可以重新描述为:

(6)

为了提高计算效率,考虑所求得的解u*必然是Gs中的关节节点,[6]而不必在所有节点中搜索.所谓关节节点是指其本身失效会增加网络连通子图数目的节点.根据文献[8],图G的连通子图数目可以由拉普拉斯矩阵L的最小特征值λ1(G)=0的重数Nλ1(G)求得.因此,仅考虑单个网络时,图G的关节节点集合AC可表示为:

(7)

而在交互网络中,由自身或耦合节点失效而引起连通子图数目增加的节点都可以认为是关节节点.由于篇幅所限,具体算法不在本文中讨论.根据式(7)求得的Gs和Gc中关节节点的集合分别为ACs和ACc,其流程如图2所示.

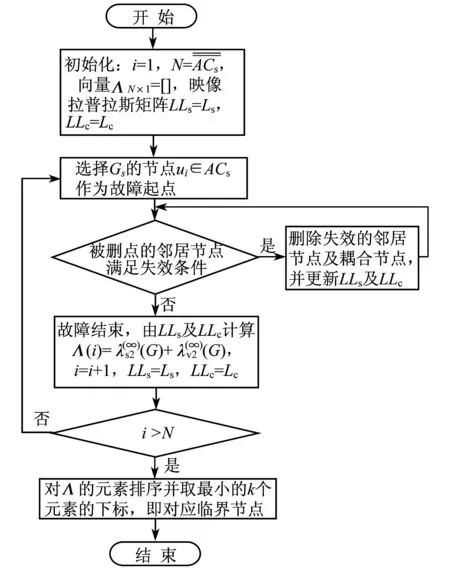
图2　 GS- AN算法流程

需要说明的是,GS-AN算法中用已失效点的邻居节点是否满足其邻居节点失效比例大于阈值1/3作为故障继续传播的判据,但这并非是惟一选择.根据实际情况也可选用其他的判据,而不影响到算法的主体性能.引发故障的初始节点可以有多个,仍可以采用与GS-AN算法中类似的故障传播机制.

4仿真结果

仿真实验中网络模型的Gs分别采用节点数目为30,57,118,300的IEEE BUS系统,Gc采用与Gs点数相同的无标度模型,幂律指数β取2.2,先将两个网络中的节点按度排序,前50%的节点按序产生一条耦合边.表1给出了IEEEBUS系统的代数连通性.[10]

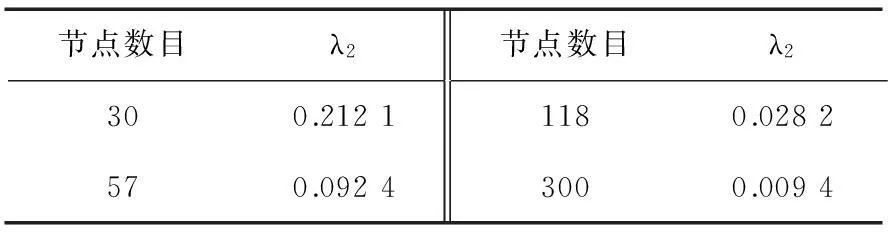
表1　 IEEE BUS系统的代数连通性

图3为不同节点数目下4个系统的性能比较.由图3可知，较少的节点系统其λ2有较快的收敛速度,这是因为300-BUS系统本身的λ2已经很小,而其节点和边的数目又是最多的,因此其故障传播速度最慢,故其λ2下降速度不明显.但最后的收敛点4个系统并无太大差别,这说明同样数目的临界节点失效在300-BUS系统中会引起更严重的后果,由此证明300-BUS系统的鲁棒性最差,这与它具有最小的λ2是一致的.这一结论也提示我们,电网规模并不是越大越好,越大的电网可能越脆弱.

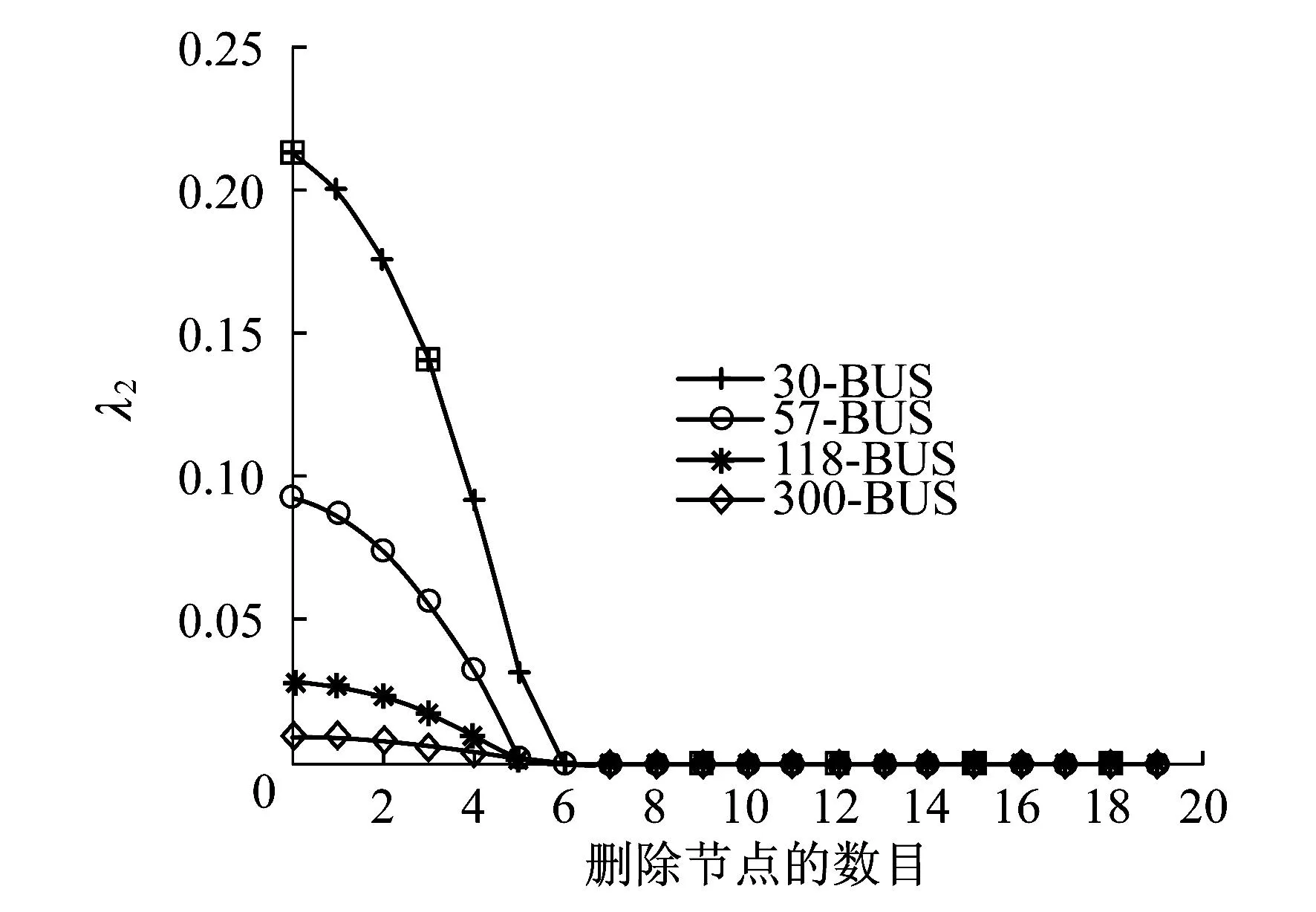
图3　不同节点数目下的算法性能

图4比较了3种算法的执行速度.由图4可以看出，本文提出的GS-AN算法更有优势,与设计算法时的预测相符.此外,3种算法有一个共同的趋势,就是在故障的前半程λ2的下降速度相对较慢,而后半程则相对较快.这是因为前半程比后半程的剩余节点多,邻接矩阵、拉普拉斯矩阵都具有相对较大的维数,因此计算的速度要慢一些.仿真结果表明，GS-AN算法在执行效率和速度上均有优势,因此该算法用于动态规划也成为一种可能.

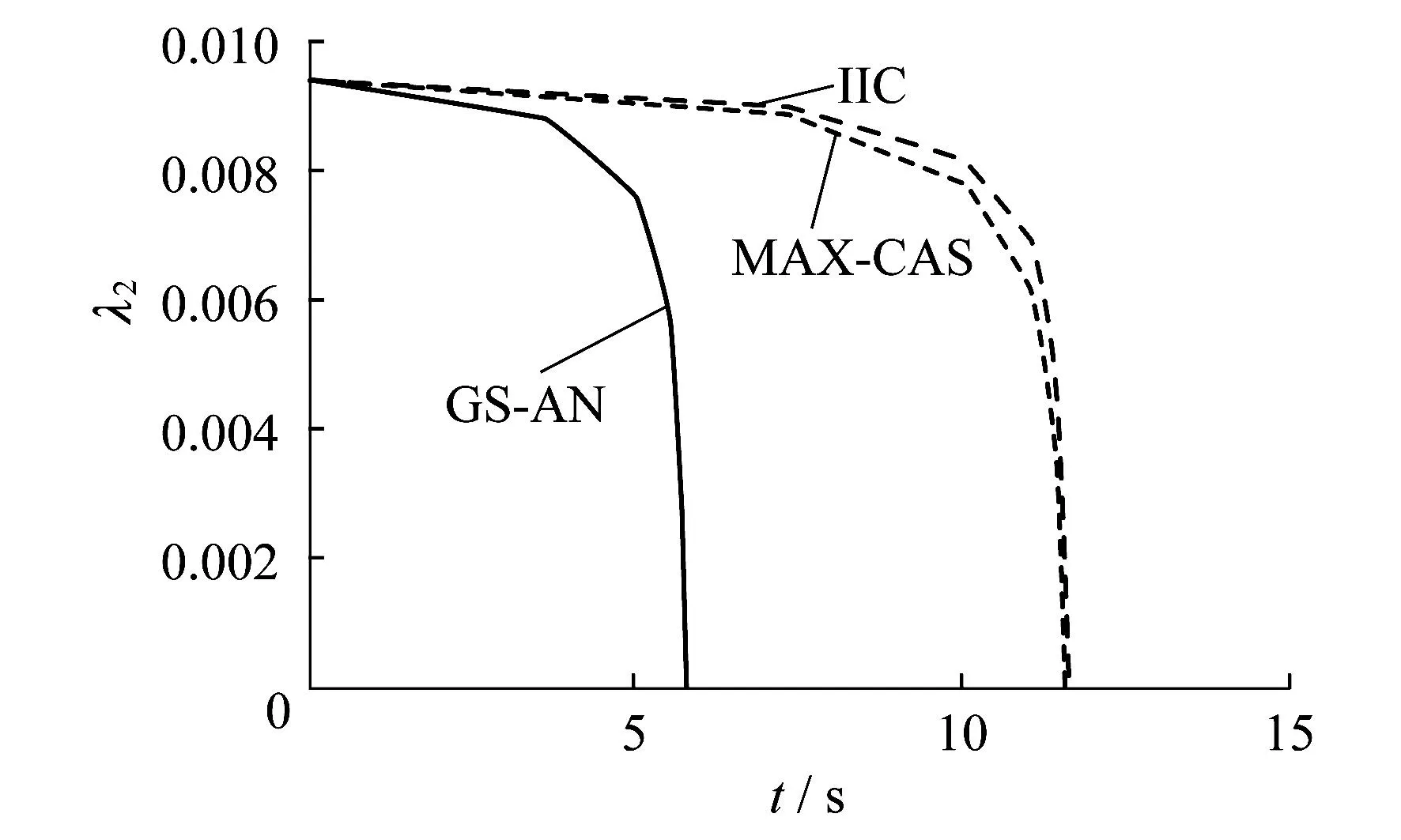
图4　3种算法的执行速度比较

5结语

在现有文献关于无标度交互网络模型研究的基础上,本文构建了与通信网耦合的交互电力网模型,并参照当前电网的实际运行情况设计了连锁故障传播机制,提出了一种基于图谱的算法来寻找交互电力网中的临界节点,为电网的安全保护提供有效的建议.与传统算法中需要复杂的程序来搜索最大连通分量不同,该算法以连锁故障后的代数连通性来评估剩余网络的鲁棒性,而代数连通性的求解可归结为特征值计算或二次规划问题,因此该算法能够以较高的效率和较快的速度寻找到对网络鲁棒性影响最大的前k个临界节点.仿真结果证明了这一优势,由此可见该种算法还有用于动态规划的潜力.

除了代数连通性以外,图谱的特征值可以从更多的角度反映图的动态和静态特征,这将是下一步的研究方向.而对于已找到的临界点,如何对其加强保护来提高鲁棒性同时又能保证其功能性,也是一个很有意义的研究课题.

参考文献：

[1]BU8LDYREVSV,PARSHANIR,PAULG,et al.Catastrophiccascadeoffailuresininterdependentnetworks[J].Nature,2010(7291):1 025-1 028.

[2]GAOJ,BULDYREVSV,STANLEYHE,et al.Networksformedfrominterdependentnetworks[J].NaturePhys.,2011,8(1):40-48.

PARSHANIR,PAULG,et al.Catastrophiccascadeoffailuresininterdependentnetworks[J].Nature,2010(7291):1 025-1 028.

[2]GAOJ,BULDYREVSV,STANLEYHE,et al.Networksformedfrominterdependentnetworks[J].NaturePhys.,2011,8(1):40-48.

[3]PARSHANIR,BULDYREVSV,HAVLINS.Interdependentnetworks:reducingthecouplingstrengthleadstoachangefromafirsttosecondorderpercolationtransition[J].Phys.Rev.Lett.,2010,105(4):048701.

[4]SCHNEIDERCM,ARAUJONAM,HAVLINS,et al.Towardsdesigningrobustcouplednetworks[R].ScientificReports3,2013:1-7.

[5]HUANGX,GaoJ,BULDYREVSV,et al.Robustnessofinterdependentnetworksundertargetedattack[J].Phys.Rev.E,2011,83:065101(R).

[6]DUNGTNguyen,SHENYilin,MYTThai.Detectingcriticalnodesininterdependentpowernetworksforvulnerabilityassessment[J].IEEETrans.OnSmartGrid,2013,4(1):151-159.

[7]CHARLESDBrummitt,RAISSAMD’Souzab,LEICHTEA.Suppressingcascadesofloadininterdependentnetworks[C].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatedofAmerica,2012(12):680-689.

[8]XIELe,CHOIDae-Hyun,KARSoummya,et al.Fullydistributedstateestimationforwide-areamonitoringSystems[J].IEEETrans.OnSmartGrid,2012,3(3):1 154-1 169.

[9]SYDNEYA,SCOGLIOC,GRUENBACHERD.Theimpactofoptimizingalgebraicconnectivityinhierarchicalcommunicationnetworksfortransmissionoperationsinsmartgrids[C]∥InnovativeSmartGridTechnologies(ISGT),IEEEPES,2013,1(6):24-27.

[10]CHOPADEP,BIKDASHM.AnalyzingsmartpowergridandSCADAnetworkrobustnessusingthenodedegreedistributionandalgebraicconnectivityundervulnerabilityandWMDattacks[C]∥HomelandSecurity(HST),IEEEConferenceonTechnologies,2012:13-15.

[11]UniversityofWashington.Powersystemstestcasearchive[EB/OL].[2014-09-15].http:∥www.ee.washington.edu/research/pstca.

[12]FIELDERM.Algebraicconnectivityofgraphs[J].CzechoslovakMath,1973,98(23):298-305.

[13]BIYIKOGLU,TURKER,LEYDOLD,et al.LaplacianEigenvectorsofGraphs[M].Berlin:Springer,2007:15-26.

[14]JAMAKOVICA,UHLIGS.Influenceofthenetworkstructureonrobustness[C]∥15thIEEEInternationalConferenceonNetworking,2007:278-283.

BULDYREVSV,HAVLINS.Interdependentnetworks:reducingthecouplingstrengthleadstoachangefromafirsttosecondorderpercolationtransition[J].Phys.Rev.Lett.,2010,105(4):048701.