应用DFIG-PSS改善电力系统低频振荡
应用DFIG-PSS改善电力系统低频振荡
边晓燕, 耿艳
(上海电力学院 电气工程学院, 上海200090)
摘要:在双馈异步风力发电机组中加装电力系统稳定器(DFIG-PSS)以提高系统阻尼,并分析了DFIG-PSS抑制低频振荡的原理,总结了4种典型的PSS模型和不同DFIG的控制方案下DFIG-PSS的输出接口位置,以及DFIG-PSS的输入信号.通过在含DFIG风电场的3机9节点系统中的仿真分析,表明DFIG-PSS对区域内振荡和区间振荡均有改善效果,且DFIG-PSS安装位置的不同,对低频振荡的改善程度也存在差异.
关键词:电力系统; 稳定器; 低频振荡
收稿日期:2014-09-24
作者简介:通讯耿艳(1989-),女,在读硕士,吉林长春人.主要研究方向为含风电场电力系统小干扰稳定,低频振荡.E-mail:gfx19891025@163.com.
中图分类号:TM712文献标志码: A
ApplicationofDFIG-PSStoImprovingLow-frequencyOscillationinPowerSystem
BIANXiaoyan,GENGYan
(School of Electrical Engineering, Shanghai University of Electric Power, Shanghai200090, China)
Abstract:A power system stabilizer is installed in doubly-fed induction generator for improving power system damping.The principle of suppressing low frequency oscillation of DFIG-PSS is analyzed.Four kinds of typical PSS model as well as output interface location of DFIG-PSS under different control scheme of DFIG and input signals of the DFIG-PSS are summed up.Finally,through the simulation analysis,the intra-area oscillation and inter-area oscillation are improved through DFIG-PSS being verified,and various installation positions of DFIG-PSS have different degrees of improvement for low-frequency oscillation.
Keywords:powersystem;stabilizer;lowfrequencyoscillation
近年来,我国的风电发展迅速,由于风电机组出力具有随机性和波动性等特点,使得电力系统低频振荡成为影响系统安全稳定的重要问题之一.
众所周知,低频振荡问题是由于系统缺乏阻尼造成的,在传统的同步发电机的励磁系统中安装电力系统稳定器(PowerSystemStabilizer,PSS)可以改善系统的阻尼,风电机组的大规模接入,要求风电机组自身为电力系统提供阻尼.
在传统的同步发电机组中,励磁控制系统只能控制转子磁链相量的幅值,不能控制转子磁链相量的位置,而双馈感应电机(DoubleFedInductionGeberator,DFIG)风电机组可以控制转子磁链相量的幅值和位置,因此DFIG风电机组比同步发电机组拥有更大的控制能力.通过在风电机组的合适位置安装电力系统稳定器的控制环,并适当地选取输入信号,然后进行调节,可以大幅增加系统的阻尼.DFIG风电机组采用的控制方案对其提供阻尼的能力具有重大作用.[1]
本文对DFIG风电机组的控制方案进行了总结,指出了在不同的控制方案中DFIG-PSS输出接口的位置,并归纳了DFIG-PSS的输入信号.最后,通过算例分析表明了DFIG-PSS对区内振荡和区间振荡均有明显的改善,并且DFIG-PSS接入位置的不同,其改善效果也有区别.
1DFIG-PSS抑制低频振荡的原理
在DFIG的控制方案中加入辅助的PSS控制环,可以大大加强系统的阻尼.
1.1 DFIG对系统阻尼的影响
为便于分析,对通用测试系统[2]中DFIG采用转子磁链幅值和相角控制方案进行考察,并假定母线电压的模值是恒定的,这样,输电线路的功率变化仅与相角的变化有关.[1]在DFIG中,通过控制转子电压的模值和相位来实现对电压和输出功率的控制.
转子磁链的dq分量分别为(以下均为标么值)
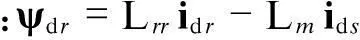
ψqr=Lrriqr-Lmiqs
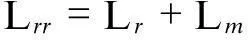
式中:ψdr,ψqr——转子磁链d轴和q轴分量;
idr,iqr——转子电流的d轴和q轴分量;
ids,iqs——发电机定子注入电流的d轴和q轴分量;
Lr——转子的漏感;
Lm——定子和转子之间的互感.
因此,转子电流dq分量的表达式为:

(1)
(2)
转子电压的dq分量分别为:
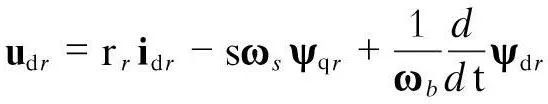
(3)
(4)
式中:udr,uqr——转子电压d轴和q轴分量;
ωs——同步转速;
ωb——转速基准值;
rr——转子电阻;
s——转差.
将式(1)和式(2)代入式(3)和式(4),得到:
(5)
(6)
暂态电抗后电势的dq分量定义为:
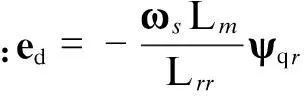
(7)
(8)
式中:ed,eq——暂态电抗后电势的d轴和q轴分量.

(9)
(10)
式中: Ls——定子漏感;
X——开路电抗,X=ωsLss,Lss=Ls+Lm;
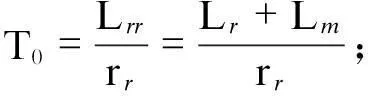
X′——DFIG的暂态电抗.
结合式(9)和式(10),内电势的矢量微分方程可以表示为:
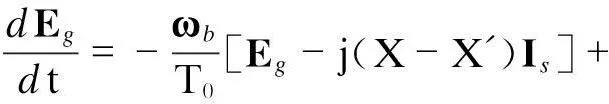

式中:
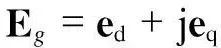
Is=ids+jiqs
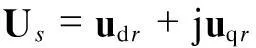
也即:

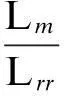
(11)
在式(11)中,Eg为暂态电抗后电势的矢量(发电机内电势),其幅值由转子磁链矢量Ψr的幅值决定.Ψr可以通过调节转子电压矢量Ur进行控制.由式(11)可以看出,Ur的改变会导致暂态电抗后电势Eg的改变,而Eg是在定子中产生的,这样就会影响DFIG的机端电压和输出功率.此外,T0=2.5 s,且由于ωs=2πf,等式的右边起主导作用的是后面两项.
假设Eg对Ur改变的响应非常快速,因此:

假定转子电压Ur的相角δr的改变会瞬时改变暂态电抗后电势Eg的相角δg.由于功率控制环中PI环节的积分项在系统振荡频率下对控制器的输出具有相对较小的影响,因此可以忽略不计.为了阻尼分析,功率环的传递函数可以近似为kpp+(kip/s)≈Kp,kpa+(kia/s)≈K,且ga(s)≈1/(1+sT),暂态电抗后电势的相角δg可以近似为δg≈δr.
由控制器作用而引起的发电机输出功率的变化为:

线性化得到:

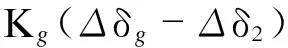
由转差率变化引起的功率变化为:
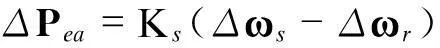
式中:


1.2 DFIG- PSS抑制低频振荡的原理
图1为转子磁链幅值和相角控制方案的功率控制环.
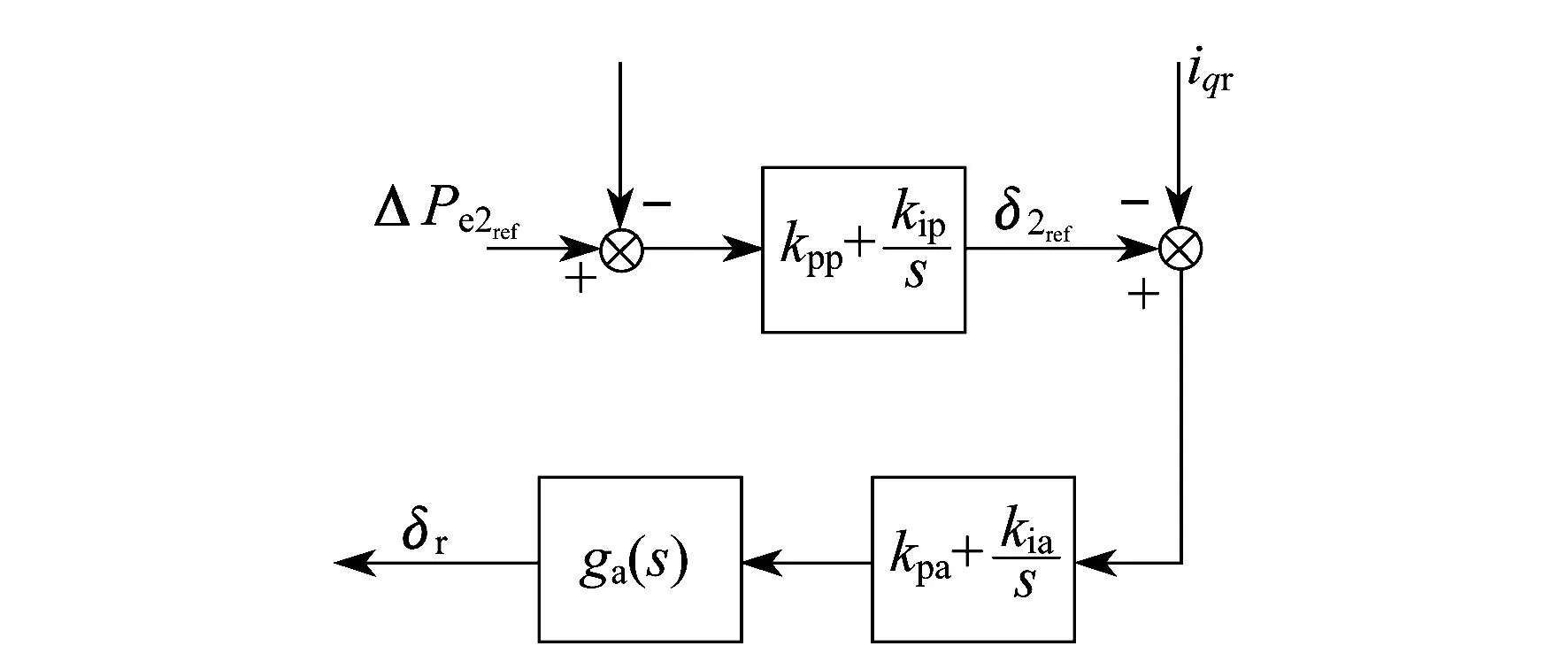
图1 转子磁链幅值和相角控制方案
功率环中所包含的滞后环节保证了DFIG具有小的正阻尼作用.对于通用测试系统,图2所示的矢量图表明,如果PSS的作用是放大功率矢量ΔPe2并将其沿逆时针方向旋转,那么DFIG对系统阻尼的作用就会增大.功率矢量沿负虚轴方向的分量ΔPe2ω增大,从而使得发电机1功率矢量沿正虚轴方向的分量ΔPe1ω也增大.从同步发电机的观点来看,这表示与转子速度振荡同相位的功率分量增大了,因而阻尼功率也增大了.在振荡状态下,DFIG注入系统的功率变化可以激发出同步发电机的附加阻尼.

图2 PSS提高发电机1阻尼时的系统矢量示意
24种典型的PSS模型
到目前为止,共有4种典型的PSS模型,[3]分别为CPSS模型、单神经元PSS模型、自适应PSS模型和多频带PSS模型,其中多频带PSS模型如图3所示.

图3 多频带 PSS模型
由于多频带PSS模型对阻尼比概率分布函数的改善效果较为明显,[3]并具有简单易懂的优点,因此本文在算例分析中采用了多频带PSS模型.
3DFIG的控制方案及DFIG-PSS的安装位置
3.1 电流模式控制
在电流模式控制中,转子电流的q轴分量用于调节转矩,d轴分量用于调节功率因数或机端电压.
3.1.1转矩控制
转矩控制器的目标是根据风速的变化来调节发电机的电磁转矩,使得风电机组运行在期望的参考点上.
3.1.2电压控制
电压控制方案一般采用转子侧变流器来实现机端的电压控制或功率因数控制,也可以通过网侧变流器实现无功功率注入,但更倾向于采用转子侧变流器来实现DFIG的电压控制.主要原因如下.
通过转子的无功功率为:

当Qr归算到定子侧时有:

(12)
由式(12)可以看出,注入转子电路的无功功率被有效地放大了1/s倍.
3.2 转子磁链幅值和相角控制
该控制方法通过调节转子磁链矢量的幅值和相角来对发电机的端电压和输出功率进行控制,其结构如图4所示.从图4可以看出,转子磁链幅值和相角控制器由两个不同的环组成:一个用于控制端电压,而另一个用于控制发电机的输出功率.其优点是功率控制环与电压控制环之间的相互影响较小.
功率控制环中,功率参考值Pe_ref是由风力机的最大功率捕获特性曲线(功率-转速特性)决定的.电压控制环和功率控制环都采用PI控制器,其中电压控制环中还增加了额外的超前-滞后补偿环节,以保证合适的闭环稳定裕度.

图4 转子磁链幅值和相角控制器模块示意
3.3 转子侧变频器控制
转子侧变频器控制包括转子磁链幅值和相角控制以及电流模式控制中的电压控制.转子侧变频器的一般控制框图及PSS的接入位置见图5.

图5 转子侧变频器控制框示意
图5中,idr_ref和iqr_ref分别表示转子电流控制参考值,Pref是有功功率控制参考值,其他为比例和积分系数.在DFIG-PSS的输出接口位置1和位置3时,采用合适的方法调节DFIG-PSS的参数,可以适当增大系统的阻尼,抑制电力系统振荡.文献[4]基于暂态能量函数分析原理,提出双馈风电场模糊附加阻尼控制策略,结果表明,风电机组无功功率环模糊附加阻尼控制在抑制传输线有功功率振荡的同时,会显著改善风电机组轴系扭矩的振荡,使电力系统区间低频振荡与风电机组传动链轴系扭振都受益.
4DFIG-PSS的输入信号
DFIG-PSS的输入信号可以选取双馈感应电机的转差、转子转速、定子电磁功率、系统频率或终端电压.文献[5]采用双馈感应电机转差为输入信号,以调节转子电压相角;文献[6]采用终端电压作为PSS的输入信号;文献[7]采用定子电磁功率作为PSS的输入信号,指出使用定子电磁功率作为PSS的输入信号,相比使用滑差或者网络频率,PSS的相位补偿要求更简单.
5算例分析
图6为3机系统单线结构示意,该系统是在IEEE3机9节点系统[8]的基础上修改而来的,其中风电场由66台1.5MW单机容量的双馈感应风力发电机组成,总容量为99MW,双馈风力发电机组参数见参考文献[9]附录,各节点编号标于图6中.

图6 3机系统单线结构示意
同步发电机组采用3阶模型,其励磁系统和原动机采用文献[10]所示模型,3个负荷的日负荷曲线、同步发电机的有功出力和电压运行曲线、平衡机的电压运行曲线见参考文献[10].风电场的有功和电压运行曲线如图7所示.
为了防止同步发电机组中PSS与DFIG-PSS之间的负相互作用,同步发电机组中均不安装PSS.利用Fortran编程,求得系统的特征根,原系统的部分特征根见表1,模态分析图见图8.
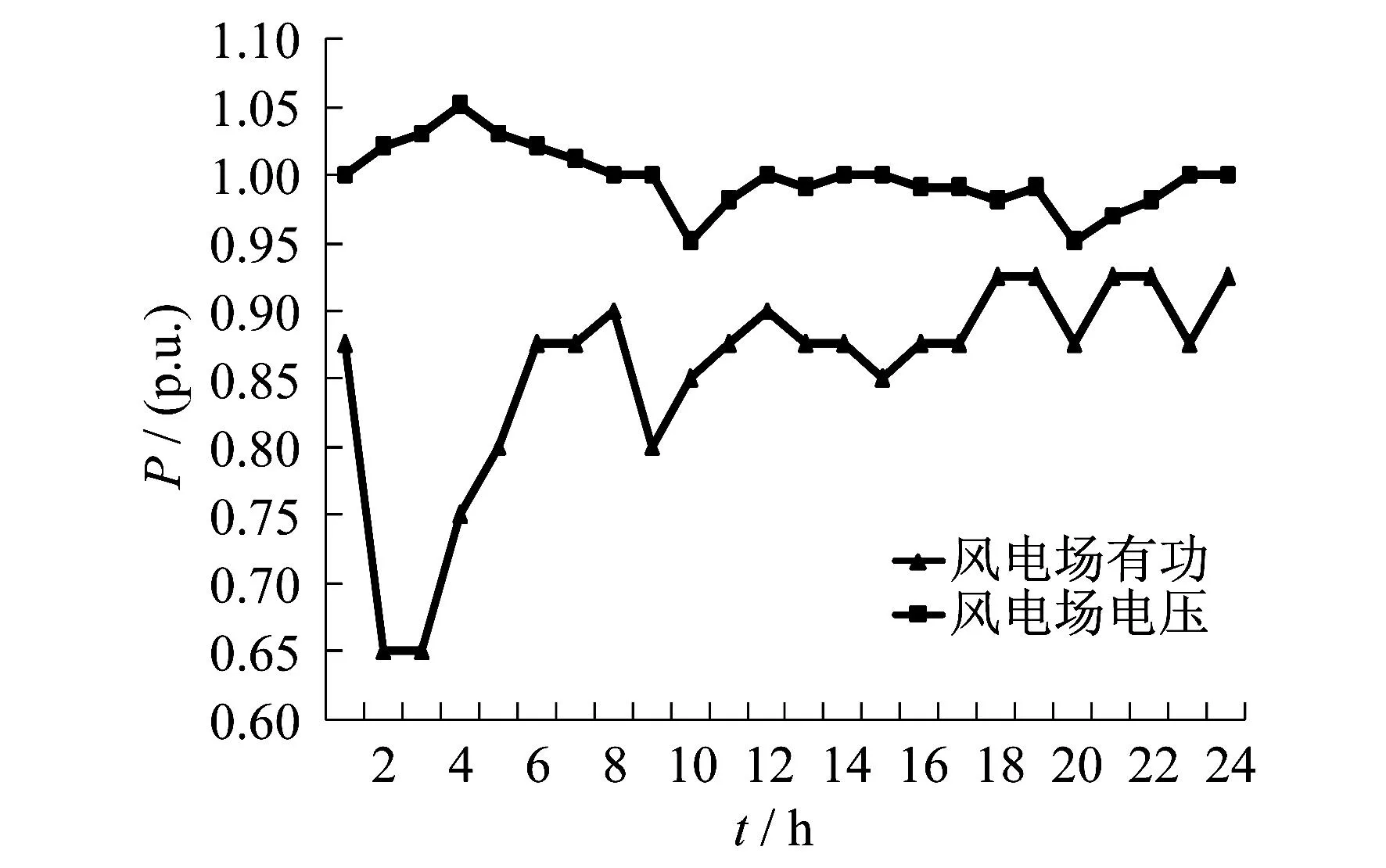
图7 风电场运行曲线
从振荡频率和模态分析图可以看出,模态1和模态2属于区域内振荡模态,模态3属于区间振荡模态.

表1 原系统机电振荡特征值
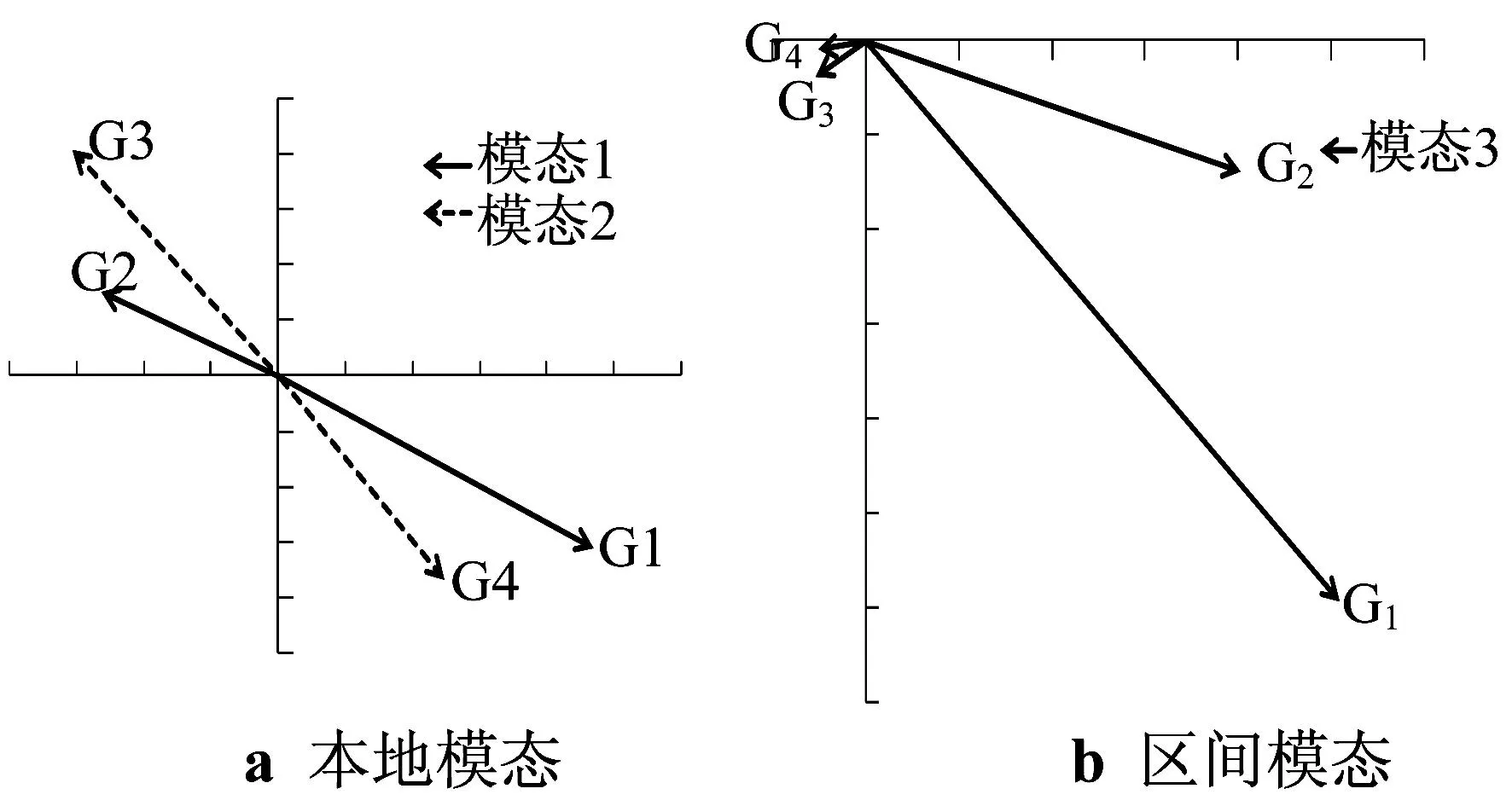
图8 机电振荡模式
将DFIG-PSS的输出端接在图5中的位置1和位置3,模型采用上述的多频带PSS模型,由于需要改善3个频带,因此频带数选为3.选择定子电磁功率作为DFIG-PSS的输入信号.PSS参数的选取按文献[3]中的方法.系统机电振荡特征值分别如表2和表3所示.比较表2和表3可知,DFIG-PSS的输出端接口所在位置不同,模态1、模态2和模态3的阻尼比虽然均有所提高,但改善效果不同;此外,DFIG-PSS对区域内振荡和区间振荡均有改善效果.

表2 DFIG- PSS接入位置1后系统机电振荡特征值

表3 DFIG- PSS接入位置3后系统机电振荡特征值
6结语
本文在分析DFIG-PSS抑制低频振荡原理的基础上,给出了在不同DFIG控制方案中DFIG-PSS的输出接口位置以及DFIG-PSS的输入信号.通过仿真分析验证了DFIG-PSS对抑制低频振荡的作用,以及DFIG-PSS的输出接口位置对改善低频振荡效果的影响.
参考文献:
[1]徐政.风力发电的模拟与控制[M].北京:机械工业出版社,2010:114-118.
[2]ANAYA-LARAO,HUGHESFM,JENKINSN.Genericnetworkmodelforwindfarmcontrolschemedesignandperformanceassessment[C]∥ProceedingsofEWEC2004 (EuropeanWindEnergyConference),London,2004:112-116.
[3]和萍,文福拴,薛禹胜,等.4种电力系统稳定器的性能比较[J].电力系统自动化,2013,37(3):30-37.
[4]李辉,陈洪文,杨超,等.双馈风电场模糊附加阻尼控制策略[J].中国电机工程学报,2013,33(31):51-57.
[5]关宏亮,迟永宁,戴慧珠,等.并网风电场改善系统阻尼的仿真[J].电力系统自动化,2008,32(13):81-85.
[6]NGELOMendonca,PECASLopesJA.SimultaneoustuningofpowersystemstabilizersinstalledinDFIG-basedwindgeneration[C].PowerTech,2007IEEELausanne,2007:219-224.
[7]MICHAELHF,ANAYA-LARAO,JENKINSN,et al.ApowersystemstabilizerforDFIG-basedwindgeneration[J].IEEETransactionsonPowerSystems,2006,21(2):763-772.
[8]TSECT,TSOSK.Algorithmforpowersystemdynamicstabilitystudiestakingaccountthevariationofloadpower[J].ElectricalPowerSystemResearch,1998,46(3):221-227.
[9]WUF,ZHANGXP,GODFREYK,et al.Smallsignalstabilityanalysisandoptimalcontrolofawindturbinewithdoublyfedinductiongenerator[J].IETGenerationTransmission&Distribution,2007,1(5):751-760.
[10]WANGKW,CHUNGCY,TSECT,et al.Improvedprobabilisticmethodforpowersystemdynamicstabilitystudies[J].IEEEGenerationTransmissionandDistribution,2000,147(1):37-43.
(编辑胡小萍)
DOI:10.3969/j.issn.1006-4729.2015.04.009


