基于展开图的安全网控制器设计

基于展开图的安全网控制器设计

方伟波，赵志诚

(太原科技大学电子信息工程学院，太原 030024)

摘要：针对一类特殊Petri网—安全网，将Petri网展开技术应用于控制器设计，研究能实现给定性能指标的最大容许控制器的设计问题。引入了控制变迁集的概念，得到了基于展开图的逻辑型控制器，在此基础上，结合Petri网展开原理，设计出原网上的结构型控制器，方便工程人员理解并能节省在线运行时控制动作的计算时间。

关键词：离散事件系统；Petri网；安全网；展开图；控制器

收稿日期：2015-03-18

作者简介：方伟波(1989-)，男，硕士研究生，主要研究方向为离散事件系统建模与控制。

中图分类号：TP301文献标志码：A

离散事件系统(DES)是一个在离散时间由事件驱动的人造系统。现代社会常见的离散事件系统有网络购物过程、通信网络系统、交通控制系统、制造系统、物流自动化系统等。DES起源于上世纪八十年代初制造系统工程方面的研究。DES系统性能分析常用数学模型有随机过程模型(如马尔科夫链、排队论等)，系统综合的数学模型则有自动机、形式语言和Petri网等[1]。

随着离散系统监控理论[2]的发展，人们发现自动机和形式语言模型很难克服计算复杂性问题，特别是针对大系统时缺点明显。因此，越来越多的学者将目光转向了Petri网。与自动机比，Petri网具有更高的语言复杂性，是正规语言的严格超集，对系统的描述更加紧凑。另外，Petri网还可以进行模块化综合[3]。

DES控制器类型分为逻辑型控制器和结构型控制器。以自动机和形式语言为工具得到的往往是逻辑型控制器，以Petri网为工具既可得到逻辑型控制器，也可得到结构型控制器。与逻辑型控制器相比，结构型控制器具有不需要在线计算、相同的Petri网演化算法可同时运用于被控对象和控制器子网的优点。目前，基于Petri网的DES控制方法比较经典的有Moody和Antsaklis等人提出的基于Petri网关联矩阵的库所不变量法[4]；Li和Wonham提出的向量离散事件系统(VDES)法[5]；Zhou和Li等人提出的信标法[6-8]；Holloway和Krogh等人提出的基于受控Petri网的路径代数法[9]。其它关于离散系统监控理论方面的研究主要有柔性制造系统的死锁避免以及活性研究[10-11]。

以上的几类控制器设计方法对特定Petri网建模的DES且满足特定条件的监控问题是有效的，但存在一些共同问题：较强的适用条件，应用范围受限，计算效率有待提高，且大多得到的控制律不是最大容许能控的，在保证系统活性方面效果不理想。这主要是由于以上几种理论的状态搜索大都基于Petri网的可达图，这是一种穷举法，计算效率低下，易导致状态空间爆炸问题。为了避免这一问题，有学者提出了Petri网展开理论[12]，实现以有限研究无限的目标，特别是对于具有不可控变迁的系统而言，将大大降低计算复杂性。

Giua等人针对普通安全网的禁止状态问题，利用Petri网展开理论，提出了在展开图上直接添加控制库所的方式得到控制策略[13]，但是获得的控制策略还不是结构型控制器，本文在前人研究的基础上，综合出原网上等价的控制结构，方便工程人员理解应用。

1Petri网及其展开理论

1.1Petri网

Petri网可对并发、异步、分布、并行、不确定和随机系统建模，其图形化的表示形式直观易理解。

定义1：Petri网

一个Petri网可以定义为四元组PN=(P，T，F，W)，其中，P={p1，p2，p3…}代表库所的有限集合，T={t1，t2，t3…}代表变迁的有限集合，F(P×T)∪(T×P)是代表流关系的弧的集合，W∶F→{1，2，3…}是弧的权函数，且满足P∩T=Ø，P∪T≠Ø。•t={p/(p,t)∈F}，称为变迁t的输入库所集合，t•相应的称为变迁t的输出库所集合，•p={t/(t,p)∈F}称为库所p的输入变迁集合，p•为库所p的输出变迁集合。

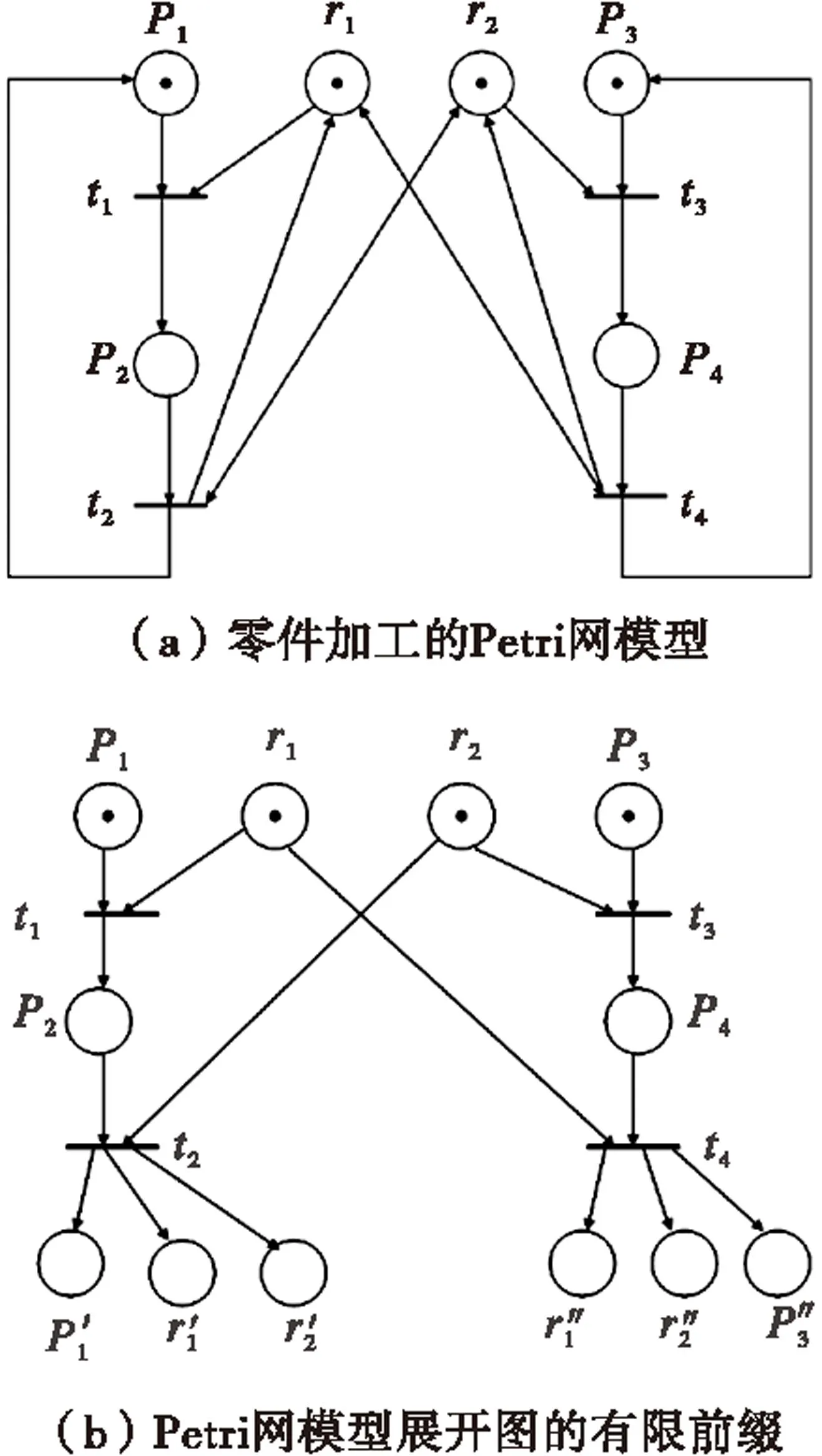
1.2Petri网展开理论

展开图法的关键在于构造Petri网展开图的有限前缀，且该图能完全表达Petri网的所有可达标识。

定义2：事件网[12]

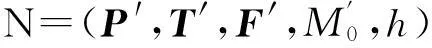
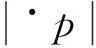
(2)F的传递闭包是非周期的，不存在自我冲突的变迁t∈T；

(3)∀t∈T′∶h(•t)=•h(t)，且h(t•)=h(t)•；

(4)∀t1,t2∈T′，若h(t1)=h(t2)，•t1=•t2则t1=t2；

(5)h(M0′)=M0.

事件网中元素间的三类关系如下：

(1)因果，x1x2)；

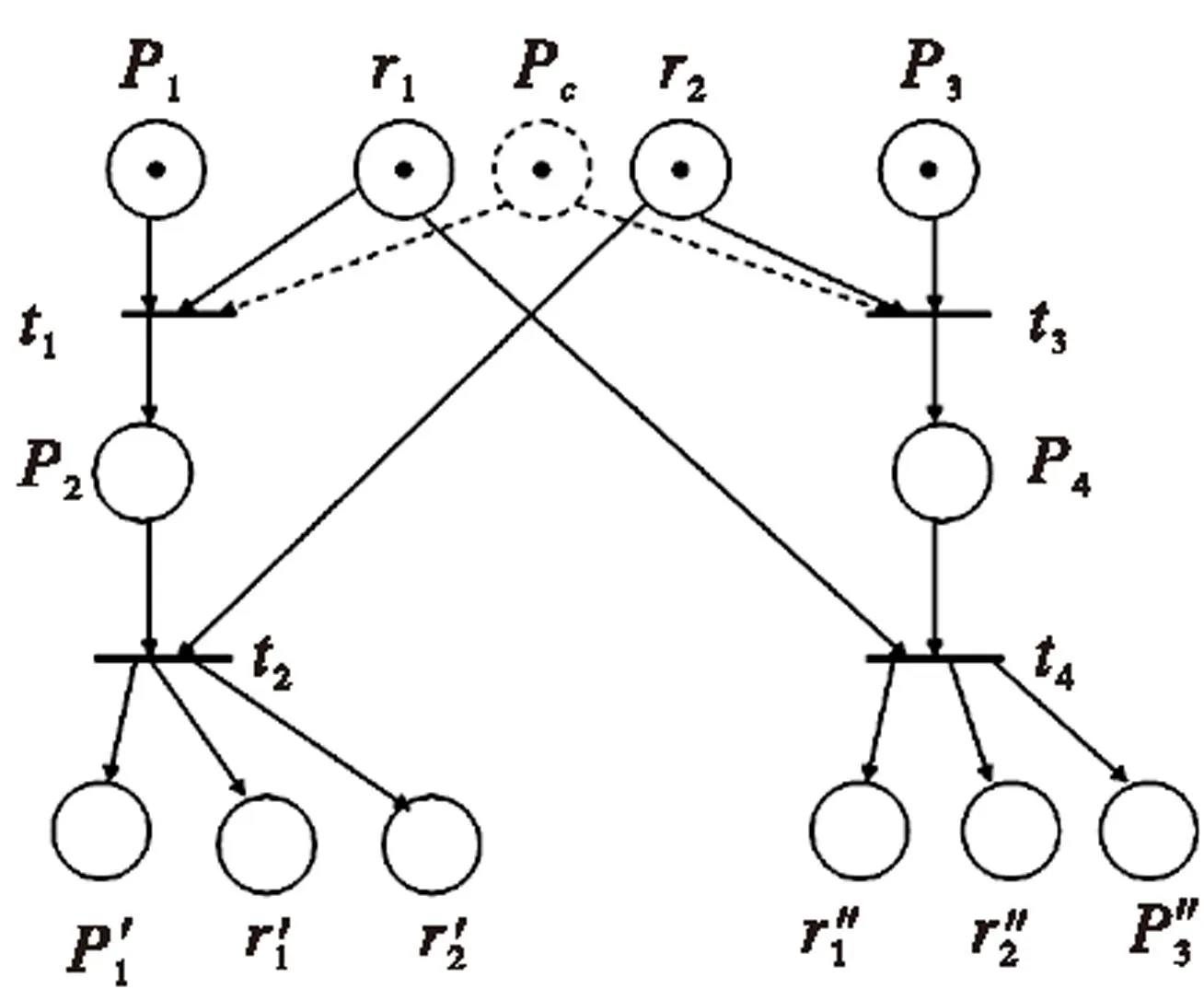
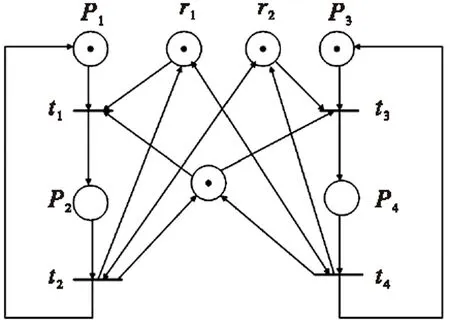
(2)冲突，x1#x2，如果∃t1,t2∈T,•t1∩•t2≠Φ且ti

(3)并发，x1‖x2，如果x1，x2既不是前后关系也不是冲突关系。

定义3：配置

变迁集合C是一个配置，如果:

(1)若t∈C，t′

(2)变迁集合C是无冲突的，即任意t1，t2∈C，不存在t1#t2

令[t]={t′∈T′|t′•C，Cut(C)常代表原Petri网的可达标识。在展开图中，配置代表了所有可能的行为动作。可知，若u代表原Petri网的一个标识，则必有一配置C满足M(h(Cut(C)))=u.

算法1:根据文献[12]的Petri网展开图构造方法。

(1)将PN中的每一个初始标识所在的库所复制到事件网中；

(2)从PN中选取一个变迁t；

(3)对于•t中的每个库所，在事件网中寻找其映射库所，若无法全找到，则返回(2)；若找到的库所不是并发的，也返回(2)；

(4)将t复制到事件网中，记为t′，从(3)中找到的每个库所画一条弧到t′；

(5)对于t•中的每个库所，将其映射到事件网中，并从t′画一条弧到这些库所；

重复步骤(2)-(5).

这一展开过程可以无限的进行下去，其中，定义其有限前缀意义重大。

定义4：截止变迁

变迁t∈T′是一个截止变迁，如果存在t′∈T′，[t′]⊂[t]，h(Cut([t′]))=h(Cut([t]))或h(Cut([t]))=M0.

展开图的有限前缀(用β表示)，通过移去所有截止变迁及其后继库所、变迁而得到。图1所示是一个关于某工厂加工两个零件的Petri网建模及其展开的简单例子。

库所r1，r2分别代表零件加工过程中要使用的两个工具R1，R2，库所p1，p3分别代表零件A、B处于待加工状态，库所p2代表零件A的加工占用了工具R1，库所p4代表零件B的加工占用了工具R2.从展开图中，可以较容易的看出，如果同时开始加工两个零件，系统将到达状态(p2，p4)，无法继续加工。

图1　Petri网展开实例

2基于展开图法的控制器设计

利用展开图法进行状态空间的搜索能有效避免状态空间爆炸问题，但优势是相对的，如果Petri网是低并发的，利用展开图法的效果则不是很明显，如果Petri网是高度并发的，则其展开图的规模要远小于其可达图，优势相对明显。

下面针对禁止状态问题，利用展开图法设计出原网上等价的控制结构。所谓禁止状态，就是为满足给定的系统性能指标，必须禁止系统进入某些状态，这些状态就构成了系统的禁止状态，用集合F表示。

假设禁止状态满足可达性要求，即：如果标识M∈F，若M→M′，即标识M′是从标识M可达的，则M′∈F.

乳糖通透酶是属于主要辅助因子超家族（MFS）的次级活性转运蛋白（SAT）。已经确定了胞质开放的乳糖通透酶结构。乳糖通透酶和β-半乳糖苷酶共同作用下可以加速乳糖分解。乳糖通透酶先将乳糖磷酸化后进入细胞内，并在β-半乳糖苷酶的水解作用下，分解成葡萄糖和半乳糖[33]。其中，一部分葡萄糖优先被乳酸菌代谢掉，通过EMP途径，最终产生乳酸。大肠杆菌的乳糖通透酶利用其中糖和H+结合位点交替进入膜两侧的机制来催化半乳糖苷与H+的化学计量协调[34]。

定义5：控制变迁集

对于展开图有限前缀中的标识M′，h(M′)∈F，且存在对应配置C，有Cut(C)=M′，则定义标识M′的控制变迁集：C′={t∈C|不存在t′∈C，t∈[t′]}.

从控制变迁集的定义知变迁t∈C′是并发的，下面针对展开图有限前缀中禁止状态标识M′，在展开图中直接添加控制库所达到最大容许能控。

算法2：由定义5，对于标识M′及其控制变迁集C′，其中控制变迁集包含k个变迁，则在展开图中直接添加控制库所pc，它的托肯数为k-1，且从pc处各添加一条弧指向控制变迁集C′中的对应变迁。对于多个标识情况，最终的控制库所可能出现冗余，根据Giua等人的方法，可以通过线性规划的方法去除冗余的控制库所。

通过算法2得到的控制策略是最大容许能控的，证明见文献[12].

针对图1(b)所示的Petri网展开图的有限前缀，为了使生产过程连续进行，可得到一个禁止状态为M(p2)+M(p4)=2，即F=(p2，p4)，在展开图中对应的标识为(p2，p4)，则根据算法2，得到图2所示的控制策略。

目前为止得到的只是展开图上的控制策略，考虑到展开图和原Petri网的映射关系，进一步获得原网上的等价控制结构，即原网上的结构型控制器。

算法3：针对算法2得到的控制策略，对展开图中的每一控制库所pc，t∈pc•，在原网中添加对应控制库所pc，托肯数与pc中相同，并分别添加从pc到变迁h(t)的有向弧，若存在变迁t′，t

图2　图1的控制策略

图3　图1中Petri网满足禁止状态要求的结构型控制器

对于图2，利用算法3，可以得到如图3所示的结构控制器，满足禁止状态要求。

可以证明此控制结构与运用库所不变量法得到的结构相同。

控制库所pc的托肯数uc0=1-LM0=1，局部关联矩阵Dc=-LDp=[-11-11]，同样可以得到图3中的控制器结构。

从此例可以看出应用展开法设计控制器的优势，它直接在有限的展开图上添加控制库所，得到满足给定禁止状态问题的控制策略，而不需要一一检索系统的所有状态，也不需要运用系统的关联矩阵，对大系统而言，它的关联矩阵维数是非常大的。这也是基于可达图的控制策略最迫切需要解决的问题。算法3在算法2的基础上进一步综合得到原网上的等价控制结构，相对于算法2的控制策略，算法3实现的结构控制器能节省在线运行时的计算时间，更具意义。当然本文给出的方法目前只适用于普通安全网，对于更复杂的Petri网，例如推广Petri网，由于受Petri网展开算法本身的制约，其实用性有待改进，但可以预见的是，一旦复杂Petri网的展开算法本身取得进步，本文给出的算法也就具备了实用意义。

3结论

针对一类禁止状态问题，研究了安全Petri网的控制器设计问题。利用Petri网展开图法，在前人的研究成果基础上，根据直接添加在展开图上的逻辑型控制器，综合得到原网上等价的结构型控制器，因为结构型控制器具有不需要在线计算、相同的Petri网演化算法可同时运用于被控对象和控制器子网的优点。此方法利用Petri网展开图搜索状态空间以避免状态空间爆炸问题，对于高并发的Petri网效果明显。目前的结论尚只适用于变迁完全可控的安全网，未来可将本文的结论推广至更一般的Petri网，且希望利用展开原理解决存在不可控变迁的情况下控制器的设计问题。进一步，能否在本文的算法基础上，解决基于Petri网的离散事件系统活性控制器[14-15]设计问题。

参考文献：

[1]LIZW，WUNQ，ZHOUMC.DeadlockcontrolofautomatedmanufacturingsystemsbasedonPetrinets-Aliteraturereview[J].IEEETransSyst，Man，Cybern，C，ApplandRev，2012，42(4)：437-462.

[2]WONHAMWM.SupervisorycontrolofDiscrete-EventSystems[EB/OL].http：//www.control.toronto.edu/people/profs/Wonham/Wonham.html，2014-07-01.

[3]GIUAA.PNtechniquesforsupervisorycontrolofdiscreteeventsystems[R].InProcof1stIntWorkshoponManufandPNs，Osaka，Japan，1996：1-21.

[4]IORDACHEMV，ANTSAKLISPJ.Supervisionbasedonplaceinvariants：Asurvey[J].DiscreteEventDynamicSystems：TheoryApply，2006，16(4)：451-492.

[5]LIY，WONHAMWM.ControlofVectorDiscreate-EventSystemsI-thebaseModel[J].IEEETransactionsonAutomaticControl，1993，38(8)：1214-1227.

[6]LIZW，ZHOUMC，JENGMD.AmaximallypermissivedeadlockpreventionpolicyforFMSbasedonPetrinetsiphoncontrolandthetheoryofregions[J].IEEETrans.Autom.Sci.Eng.，2008，5(1)：182-188.

[7]LIZW，ZHOUMC.ControlofelementaryanddependentsiphonsinPetrinetsandtheirapplication[J].IEEETransSyst，Man，Cybern，A：Syst，Humans，2008，38(1)：133-148.

[8]LIZW，ZHOUMC.OnsiphoncomputationfordeadlockcontrolinaclassofPetrinets[J].IEEETransSyst，Man，Cybern，A：Syst，Humans，2008，38(3)：667-679.

[9]HOLLOWAY，KROGHLEBH.Onclosed-looplivenessofdiscrete-eventsystemsundermaximallypermissivecontrol[J].IEEETransactionsonAutomaticControl，1992，37(5)：692-697.

[10]LIZW，LIUGY，HANISCHMH.etal.DeadlockpreventionbasedonstructurereuseofPetrinetsupervisorsforflexiblemanufacturingsystems[J].IEEETrans，Syst，Man，Cybern，A：Syst，Humans，2012，42(1)：178-191.

[11]HUHS，ZHOUMC，LIZW.Livenessandratio-enforcingsupervisionofautomatedmanufacturingsystemsusingPetrinets[J].IEEETransSyst，Man，CybernA，Syst，Humans，2012，42(2)：392-403.

[12]JAVIERESPARZA，KEIJOHELJANKO.Unfoldings——Apartialorderapproachtomodelchecking[M].Springer，Berlin，2008.

[13]GIUAA，XIEXL.ControlofsafeordinaryPetrinetsusingunfolding[J].DiscreteEventDynamicSystems，2005，15(3)：349-373.

[14]CHENYF，LIZW，ZHOUMC.Mostpermissiveliveness-enforcingPetrinetsupervisorsforflexiblemanufacturingsystems[J].IntJProdRes，2012，50(22)：6357-6371.

[15]SREENIVASRS.Ontheexistenceofsupervisorypoliciesthatenforcelivenessinpartiallycontrolledfree-choicePetrinets[J].IEEETransactionsonAutomaticControl，2012，57(2)：435-449.

Controller Design for Safe Nets Based on Unfolding Graph

FANG Wei-bo，ZHAO Zhi-cheng

(School of Electronic Information Engineering，Taiyuan University of Science and Technology，

Taiyuan 030024，China)

Abstract：According to a special class of Petri net (PN)，PN unfolding-a partial-order method was used to deal with the problem about controller design for safe nets.The designed controller is maximally permissive and able to enforce the given specification.The definition about the set of control transitions was given，and an equivalent control structure of the reported controller was proposed，which was added to the unfolding net of the original one.It is easier to understand for engineers and can save the computational time on-line.

Key words：discrete event system，petri nets，safe nets，unfolding，controller