基于Petri网的BPMN工作流分析方法研究
【摘 要】BPMN工作流被广泛应用于各种办公自动化系统,本文通对BPMN工作流的Petri网建模,分析工作流系统的结构特征、运行状态、成功概率等因素,提出了基于随机Petri网的BPMN工作流分析方法。在对由事件、活动和关口组成的工作流的运行状态进行分析之后,根据工作流的运行状态分析工作流的执行过程,以此求得整个工作流系统的成功运行概率。这种方法不是工作流的运行路径分析,而是对工作流的各个运行状态进行数据分析。
【关键词】BPMN;工作流;Petri网;状态集
0 引言
工作流是对业务流程及其各操作步骤之间业务规则的抽象、概括和描述。工作流管理系统的功能是通过计算机技术的支持、定义、执行和管理工作流,协调工作流执行过程中活动之间以及参与成员之间的信息交互[1-2]。工作流管理系统现在被广泛应用于金融、电信、教育、医疗等需要实现办公自动化的领域。BPMN(Business Process Model and
Notation)规范定义了用于描述工作流的符号及模型,目的是让流程的定义具有可移植性,使得满足规范的流程可以移植到遵守BPMN标准的供应商如JPBM或Activiti环境中[3-4]。将Petri网运用于BPMN工作流运行状态的分析中,是Petri网理论在BPMN工作流建模中的应用和扩充[5]。
1 BPMN的Petri网建模
BPMN2.0规范中定义了标准的图形和符号,有5类基础的元素分别是流对象、数据、连接对象、泳道和制品。在对BPMN工作流的Petri网建模过程中,我们主要关注流对象中用于定义行为的三个元素:事件、活动和关口。工作流系统的整体结构和运行状态可以通过我们自定义的工作流Petri网系统(Workflow Ptetri Net System,简记为WPNS)[6]来描述。在WPNS中用S表示活动集,T表示关口变迁集,F表示顺序流集,M表示工作流状态集,TP表示关口的迁移概率,则工作流Petri网系统是一个六元组∑=(S,T;F,M;SA,TP),其中:
1)(S,T;F,M)是一个对BPMN建模的Petri网,S称为活动集(activity set),T称为关口变迁集(gateway set),M?哿S称为∑的一个工作流运行状态。
2)SA是工作流活动的批准概率,SA={A(s1),A(s2),…,A(sn)},A(si)描述的是活动被批准任务可以继续的概率。如果活动被驳回,则其驳回概率为1-A(si)。为了简化分析,若工作流被驳回重新开始视为流程失败。
3)TP是关口的迁移概率。在条件顺序流中,只有表达式结果为真,关口才会沿着这些顺序流执行。设TP={p1,p2,…,pm},pi是某个活动的后续所有关口变迁,则对任意pi∈s·,∑pi=1。如果在BPMN建模时两个活动之间是顺序流不存在关口,那么在Petri网建模时需要一个虚拟关口,此虚拟关口迁移概率pk=1。
4)若工作流在状态M通过关口变迁t,得到新状态M(记作M[t>M),则M′=(M-·t)∪t·。为了简化分析,若工作流被驳回视为流程结束。
工作流中各活动和关口有特定的前后关系。我们在WPNS中为每一个活动赋予一个批准概率系数,运行状态中某个活动的成功概率可表示为其自身批准概率与前置关口的迁移概率相乘。由于执行活动任务只需要经过一个关口即可,所以任意活动的前置关口只有一个,这个特性是由BPMN的标准规范得出的。在对BPMN工作流的Petri网建模完成后,就可以用Petri网对工作流的运行数据进行分析。Petri网模型的运行可达性、有界性和工作流系统运行的可达性、有界性是一致的,其完全状态集个数R(M0)= k<<2n。在此之后,就可以通过工作流各个运行状态的特征来描述整个工作流系统的运行特征[7]。
2 BPMN工作流状态分析
BPMN工作流运行时,因单向关口、并行关口、兼容关口的不同会产生不同的运行状态。设M∈R(M0),M是工作流Petri网系统中的一个运行状态,此状态下流程成功运行概率为A(M)。若第i个活动任务的批准概率为A(si),且其前置关口变迁执行概率为F(·si),则如前所述此状态下该工作流动态成功运行概率为A(si)×F(·si)。若在某状态下,当且仅当等待执行的活动任务全部成功执行时,流程才可以继续,任意一个任务的失败都将导致整个工作流的失败,此时工作流的成功概率为:A(M)=∏n i=1A(si)×F(·si)。若在某状态下,只要某一个处于等待执行的活动任务成功执行流程就可以继续,只有等待执行的活动任务都被驳回流程才失败,此时工作流的成功概率为:A(M)=1-∏n i=1(1-A(si)×F(·si))。如果工作流运行状态是混合状态,此时的成功概率计算可采用递归方法:对运行状态进行逐级分解,再利用前述计算方法逐级回溯,最终计算得出此运行状态的成功概率[8]。
求解整个系统的成功运行概率需要得到工作流的所有运行状态,这可以通过可达标识图解决。可达标识图的每一个结点对应工作流中的一个运行状态,所有的结点就是工作流的全部运行状态。得到工作流系统的成功运行概率还需要知道工作流运行状态的稳定概率P(Mi)。稳定概率P(Mi)可以用对应的同构马尔可夫链来求得[9]。这样,对任意Mi若成功概率为A(Mi),稳定概率为P(Mi),则工作流的整体流程成功概率可以由下面的公式得到:
A(S)=∑k i=0A(Mi)×P(Mi),其中∑i i=0P(Mi)=1
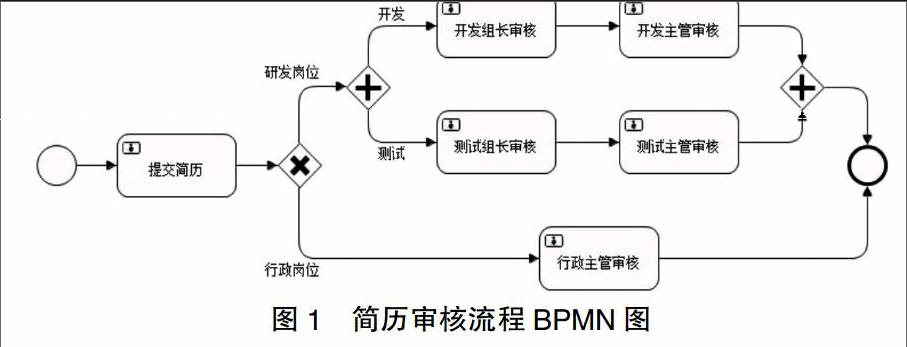
例如,图1是在符合BPMN规范的Activiti Eclipse建模工具中设计的简历审核流程图。其中,提交简历任务之后是一个单向关口,即简历审核分行政岗位和研发岗位。行政人员的简历只需要行政主管审核通过流程即成功结束。研发人员的简历又分开发人员和测试人员,需要两个部门的主管同时审核通过才可以继续。此处(下转第199页)(上接第175页)是一个并行关口,只有当两部门主管都审核成功后流程才成功结束。为简化起见流程图中省略了驳回顺序流,任一活动任务的驳回视为流程失败。
对图1的工作流进行Petri网建模,∑=(S,T;F,M;SA,TP),活动集个数S=6。注意其中的开发组长审核、开发主管审核与测试组长审核、测试主管审核是并行关口,同时有分岔和合并。依据前述的Petri网理论,包括初始状态M0=(1,0,0,0,0,0),还有5个可达状态分别是M1=(0,0,0,0,0,1),M2=(0,1,1,0,0,0),M3=(0,1,0,0,1,0),M4=(0,0,1,1,0,0),M5=(0,0,0,1,1,0)。在已知各活动任务批准概率A(si)及其前置关口迁移概率F(·si),以及假设A(si)×F(·si)=ai的前提下,可计算出工作流各个运行状态的成功概率:R(M0)=a1;R(M1)=a6;R(M2)=1-(1-a2)(1-a3)=a2+a3-a2a3;R(M3)=1-(1-a2)(1-a5)=a2+a5-a2a5;R(M4)=1-(1-a3)(1-a4)=a3+a4-a3a4;R(M5)=1-(1-a4)(1-a5)=a4+a5-a4a5。通过马尔可夫方程已知系统各运行状态的稳定概率P(Mi)=pi,则工作流系统的成功概率为:A(S)=∑k i=0A(Mi)×P(Mi)=a1*p1+(a2+a3-a2a3)*p2+(a2+a5-a2a5)*p3+(a3+a4-a3a4)*p4+(a4+a4-a4a5)*p5+a6*p6。
3 小结
JPBM和Activiti等满足BPMN规范的产品和开发工具的流行使得工作流系统的使用愈发普及,本文通过Petri网对工作流系统进行分析是对BPMN规范的延伸应用。BPMN工作流把业务流程中的任务前后组织在一起,而对BPMN的Petri网建模将其中的逻辑和规则以Petri网的模型进行恰当表示,然后对其实施计算和分析。基于Petri网运行状态的工作流分析方法通过对工作流系统的结构和运行特征进行分析,得到工作流的所有运行状态和运行数据,最后计算出工作流总体的成功概率。与静态执行路径的分析方法不同,该模型关注工作流动态运行过程中的数据分析。本文提出的模型能够简单有效地模拟工作流的运行过程并计算出工作流的相关运行数据,可以在工作流系统设计早期对其进行分析和评估,具有较高的理论价值和实践意义。
【参考文献】
[1]Wong P Y H, Gibbons J. Formalisations and applications of bpmn[J].Sci. Comput. Program.,2011,76(8):633-650.
[2]Chinosi M,Trombetta A.Bpmn:An introduction to the standard[J].Comput. Stand. Interfaces,2012,34(1):124-134.
[3]范会联.基于自定义表单的工作流过程定义分析与设计[J].计算机应用研究,2009,26(9):3372-3374.
[4]刘衍珩,钟呈祥,朱建启.工作流程中的任务委托模型[J].计算机工程,2010,36(13):260-262.
[5]吴哲辉.Petri网导论[M].北京:机械工业出版社,2006.4.
[6]郑晓东,崔志明,陈建明.基于Petri网运行状态的组件化软件可靠性分析方法[J].计算机技术与发展,2008,18(4):5-8.
[7]张友生,李雄.基于Petri网的软件体系结构可靠性分析[J].计算机工程与应用,2006,25:70-73.
[8]李光远,陈咏章.用随机Petri网对构件化软件可靠性进行早期评估[J].计算机工程与应用,2005,41(29):84-87.
[9]林闯.随机Petri网和系统性能评价(第二版)[M].北京:清华大学出版社, 2005.4.
[责任编辑:王楠]

