一种结合微粒群算法的混合MIMIC算法

一种结合微粒群算法的混合MIMIC算法

张文林，夏桂梅

(太原科技大学应用科学学院，太原 030024)

摘要：分布估计算法是基于遗传算法的基础上发展起来的一种新型的优化算法，它采用的是概率图的模型来表示基因中变量之间的关系，从而构建优良解集的概率分布模型进行采样来实现迭代进化。但是分布估计算法在问题求解过程中容易陷入局部最优，针对此缺点，引入微粒群算法，提出了一种结合微粒群算法的分布估计算法。这种算法将分布估计算法与微粒群算法的思想紧密结合起来，不仅保持了种群的多样性，而且具有更全面的学习能力，提高了算法的寻优能力以及避免早熟收敛的能力。通过对测试函数的仿真试验，表明该算法具有良好的性能。

关键词：分布估计算法；微粒群算法；MIMIC算法

收稿日期：2015-03-10

基金项目：山西省自然基金(2014011006-2)

作者简介：张文林(1989-)，男，硕士研究生，主要研究方向为最优化理论与应用；通信作者：夏桂梅，副教授，E-mail：xiaguimeiznn@163.com

中图分类号：0221文献标志码：A

分布估计算法(简称EDA)[1]是在1996年提出的一种基于概率模型的优化算法，当前已成为进化领域研究的重要内容。分布估计算法是通过一个概率模型来描述候选解在空间的分布，然后采用统计学习的手段从群体宏观的角度去建立一个描述解分布的概率模型，最后对概率模型随机采样产生新一代的种群，如此反复进行，最终实现种群的进化。根据变量之间的相关性，可以将分布估计算法分成以下三类：变量相互独立的分布估计算法、双变量相关的分布估计算法和多变量相关的分布估计算法[2]。

然而分布估计算法在进化的过程中对概率模型进行学习时，很容易对问题解空间的分布过于依靠，导致算法构建的概率模型不能够准确的表达解空间的信息，在算法多次迭代后，种群的多样性减少，并且进化的速度非常慢，每一代的改变也很小，这些情况说明分布估计算法的全局搜索能力强，而局部搜索能力弱。鉴于分布估计算法的此弱点，在生成新群体的过程中加入微粒群算法[3]，提出一种结合微粒群算法的分布估计算法(PSO-MIMIC).

1结合微粒群算法的混合MIMIC算法(PSO-MIMIC)

1.1微粒群算法

在标准的微粒群算法中，假设一个由m个粒子组成的群体在D维的空间中以一定的速度飞行，每个粒子在搜索时，考虑到了粒子本身搜索到的历史最优点，以及群体内其他粒子的历史最优点，在此基础上进行位置的更新。如文献[4]和文献[5]都是利用微粒群算法求解约束优化问题。

第i个粒子的位置可以表示为xi=(xi1,xi2，…,xiD)；第i个粒子的速度可以表示为vi=(vi1,vi2,…,viD)，其中1≤i≤m,1≤d≤D；第i个粒子经过的历史最优点可以表示为pi=(pi1,p=i2,…,piD) ；群体内所有粒子经过的最优点可以表示为pg=(pg1,pg2,…,pgD)；

每一个粒子的位置和速度按以下公式进行更新：

(1)

(2)

其中，w称为惯性权重，其表示粒子对当前速度的继承能力，选择合适的w可以使粒子具有全局搜索能力和局部搜索能力；c1和c2称为学习因子，c1表示粒子具有自我总结的能力，c2表示粒子从群体中优秀个体学习的能力，从而使得粒子向自身的历史最优点以及群体内粒子的历史最优点靠近；ξ和η是[0,1]之内的随机数。

1.2MIMIC算法

MIMIC算法[6]是最早提出的一种双变量相关的分布估计算法，它把遗传算法与统计学思想结合起来，对解空间的个体分布，利用统计学的思想来建立概率模型，避免了遗传算法中的交叉和变异等操作，减少了参数的设置，更容易求解。在MIMIC算法模型中，将随机向量中各变量之间考虑成一种链式结构，即只有相邻之间的节点间存在依赖关系，其概率模型图如下：

定义解空间概率分布模型：

(3)

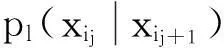
(4)

(5)

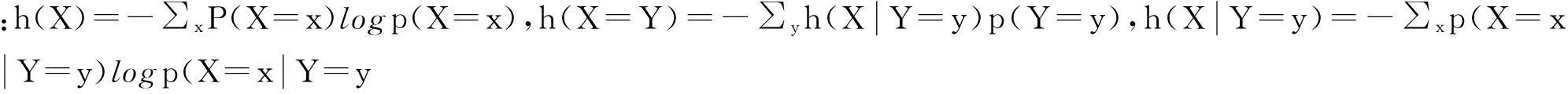
1.3PSO-MIMIC算法

针对非线性多约束优化问题[7]，本文提出了一种结合微粒群算法与MIMIC算法的PSO-MIMIC算法。新算法中每一个粒子的信息一部分来自于所有个体最优值的概率模型，另一部分来自粒子的当前解与全局最优解。这样粒子的当前解，所有个体最优值和全局最优值都参与了新解的生成过程，利用了分布估计算法的思想并且继承了微粒群算法的思想，保持了种群的多样性，同时具有更全面的学习能力，提高了算法的寻优能力以及避免早熟收敛的能力。其中，当我们对有约束条件的优化问题进行研究时，可以采用罚函数法，将约束优化问题转化成为无约束的优化问题进行求解。具体步骤如下：

Step 1对群体初始化，同时设置参数，随机的产生2n个个体作为初始群体pop°，k→0；

Step 2利用罚函数法将约束问题转化为无约束问题；

Step 3计算群体中每一个个体的适应值，若满足终止条件，则算法结束，否则转下一步；

Step 4用轮盘赌法和截断法选择n个个体作为优势群体；

Step 5将Step 4中n个个体根据设置的参数利用微粒群算法进行更新，得到M1个新个体：

Step 6将Step 4中n个个体执行以下操作：

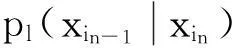
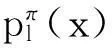
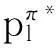
Step 7按逆序从概率模型中采样M2次(其中M2=2n-M1)，与更新后的M1个个体组成新一代群体popk+1，转Step3.

2数值试验

2.1测试函数

为了测试算法的性能，选取文献[9]中6个测试函数，并对所得结果进行比较。

函数1：

minf(x)=(x1-10)3+(x2-20)3

s.t. g1(x)=-(x1-5)2-(x2-5)2+100≤0

g2(x)=(x1-6)2+(x2-5)2-82.81≤0

13≤x1≤100

0≤x2≤100

函数2：

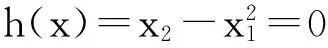
函数3：

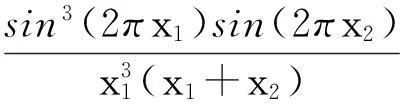
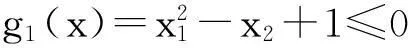
g2(x)=-x1+(x2-4)2+1≤0

0≤xi≤10,i=1,2

函数4：

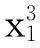
x4-x3+0.55≥0x3-x4+0.55≥0

s.t. 1000sin(-x3-0.25)+1000sin(-x4-0.25)+894.8-x1=0

1000sin(x3-0.25)+1000sin(x3-x4-0.25)+894.8-x2=0

1000sin(x4-0.25)+1000sin(x4-x3-0.25)+1294.8=0

0≤xi≤1200,i=1,2

-0.55≤xi≤0.55,i=3,4

函数5：

40792.141

s.t. 0≤85.334407+0.0056858x2x5+0.00026x1x4-0.0022053x3x5≤92

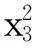
20≤9.300961+0.0047026x3x5+0.0012547x1x3+0.0019085x3x4≤25

78≤x1≤102,33≤x2≤45,27≤xi≤45,

i=3,4,5

函数6：

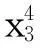
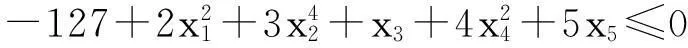
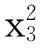
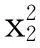
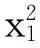
-10≤xi≤10,i=1,2,…,7

2.2参数设置

在试验中，算法的各个参数设置如下：群体规模2 000，最大迭代次数为500，精度10-3，惯性权重w=0.5，加速权重c1=c2=0.494 45，各自独立进行10次试验。

2.3试验结果及分析

表1给出了每个测试函数的最优值f(x*)以及运用本算法独立运行10次试验后的最好值，平均值及偏差。

由表1可知每个测试函数在独立进行10次试验后都能找到最优值，而且测试函数已知的最优值同本文算法求出的最优值的偏差接近于0，说明了本文算法具有有效性和可行性。但是，随着函数维数的增加，其最优值与已知最优值偏差逐渐增大，说明该算法对于维数较低的函数有较好的效果，而对于维数较高的函数还存在一定的欠缺。

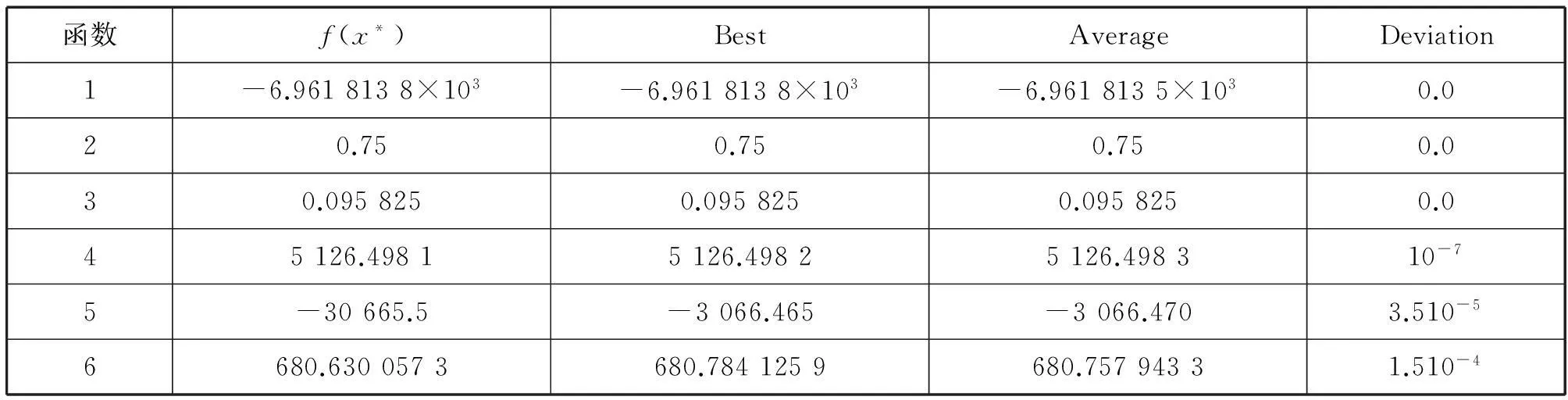
表1　测试函数试验结果

表2给出了本文算法(PSO-MIMIC)与MIMIC算法对测试函数结果与测试函数已知最优值f(x*)的比较。

由表2可以看出本文算法与标准MIMIC算法对测试函数的最好值及平均值与函数本身最优值的比较。尤其对于函数1、2、3，由本文算法得到的平均值明显比MIMIC算法得到的平均值更接近于最优值。而对于维数高的函数5和6，其结果稍次于MIMIC算法，但也能找到接近最优解的值。

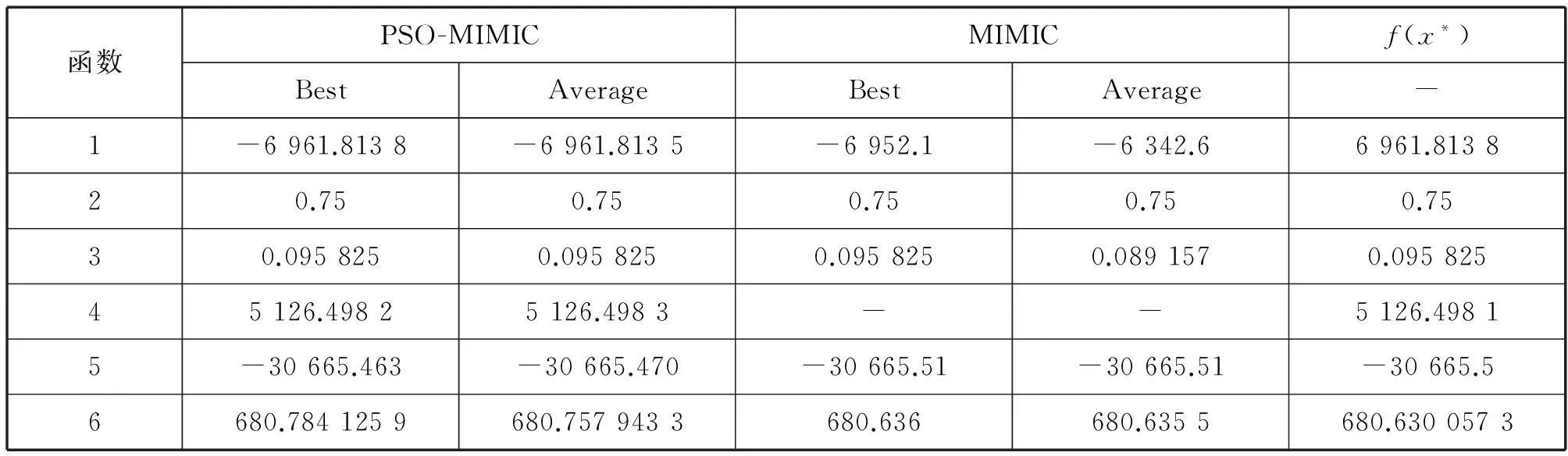
表2　PSO-MIMIC与MIMIC算法对测试函数性能的比较

图1　MIMIC关系图

图2　PSO-MIMIC关系图

图1和图2给出了本文算法与标准MIMIC算法对具有代表性的函数1、3和6从优势群体个数和进化代数的关系方面进行比较的关系图。其中优势群体个数从1 000开始，按100的个数递增，直到2 000为止，分别进行仿真试验所得结果动态图如图1、图2.由图可知，随着优势群体个数的增加，进化代数也呈增加的趋势，尤其对于函数6，其稳定性与进化代数明显优于标准MIMIC算法，试验结果初步验证了本文算法的有效性和合理性，说明本文算法具有一定的优势。

3结论

PSO-MIMIC算法充分结合了微粒群算法结构简单的特点，又克服了分布估计算法在种群进化过程中个体单一的缺点，使得原来的算法在解决优化问题时有了一定的改进。把改进后的算法应用于处理非线性约束优化问题，结果表明，本文提出的PSO-MIMIC算法具有一定的优势，能够找到满足约束条件的最优解，并且最优值与已知最优值非常接近，收敛效率很高，尤其对于维数较低的函数具有非常好的效果，而对于维数较高的函数，其效果稍次于其他算法，究其原因是在对约束条件的处理方法上导致的，如果在本算法的进化过程中能找到其他合适的处理约束条件的方法，其效果可能会更好，其方法有待于进一步研究。

参考文献：

[1]周树德，孙增圻.分布估计算法综述[J].自动化学报，2007，33(2)：115-118.

[2]叶宝林.分布估计算法的一种改进与应用[D].太原：太原科技大学学报，2011：1-81.

[3]屈向红，夏桂梅，王希云.求解约束优化问题的改进微粒群算法[J].太原科技大学学报，2012，33(5)：406-409.

[4]熊鹰，周树民，祁辉.一种新型的求解约束优化问题的微粒群算法[J].广东广播电视大学学报，2006，59(15)：32-35.

[5]李金莱，卢香清.一种求解约束优化问题的信赖域微粒群算法[J].计算机工程与应用，2011，47(10)：198-200.

[6]罗国军，张学良，郭晓东，等.MIMIC算法在非线性多约束机械优化问题中的应用[J].太原科技大学学报，2013，34(6)：440-444.

[7]吴红梅.非线性约束优化问题的信赖域算法[D].兰州：兰州理工大学，2007：1-53.

[8]DE BONET J S，ISBELL C L，VOILA P.MIMIC：Finding Optima by Estimating Probability Densities[C].In：Advances in Neural Information Processing Systems，Cambrige：MIT Press，1997，(9)：424-430.

[9]ZBIGNIEW MICHALEWICZ，MARC SCHOENAUER.Evolutionary Algorithms for Constrained Parameter Optimization Problems[J].Evolutionary Computation，1996，4(1)：1-32.

A Hybrid MIMIC Algorithm Combining With Hybrid Particle Algorithm

ZHANG Wen-Lin，XIA Gui-Mei

(School of Applied Science，Taiyuan University of Science and Technology，Taiyuan 030024，China)

Abstract：The estimation of distribution algorithm is developed on the basis of genetic algorithm；it is a kind of new optimization algorithm which uses probability graph model to express the relationship among variables to construct the gene so as to build excellent solution set of probability distribution model for sampling to realize iterative evolution.But the estimation of distribution algorithm easily falls into local optimum in the problem solving process.Aiming at this disadvantage，the particle swarm algorithm is proposed to estimate algorithm combined with the distribution of particle swarm optimization algorithm.The new algorithm combines the estimation of distribution algorithm with particle swarm algorithm，keeps the diversity of population， has more comprehensive learning ability and improves searching ability to avoid premature convergence.Through simulation test of test function， the algorithm is proved to have good performance.

Key words：estimation of distribution algorithms，hybrid particle algorithm，MIMIC algorithm