微粒群进化估值策略在多目标优化中的应用

微粒群进化估值策略在多目标优化中的应用

刘彤，孙超利，曾建潮

(太原科技大学工业与系统工程研究所，太原 030024)

摘要：作为群智能算法，微粒群算法由于在获得最优解集之前需要大量的适应值评价，从而阻碍了其在复杂的多目标优化优化问题中的应用。为了解决该问题，本文将进化估值策略引入到多目标微粒群算法中，用适应值估计代替适应值实际评价，以减少适应值实际计算次数，从而节省计算花费。实验结果表明引入进化估值策略的多目标微粒群算法可以大大减少适应值的评价次数，而相似度的评价控制机制可提高估值的准确性，从而在减少评价次数的同时提高算法的优化性能。

关键词：多目标微粒群算法；进化估值策略；相似度；适应值评价

收稿日期：2015-03-18

基金项目：国家自然科学基金(61403272)

作者简介：刘彤(1989-)，女，硕士研究生，主要研究方向为计算智能。

中图分类号：TP311文献标志码：A

多目标优化问题(MOP)广泛存在于科学实践、工程系统设计及社会生产的各个领域，其一般形式为：

MinF(X)=[f1(X),f2(X),…,fk(X)]

(1)

其中，X=[x1,x2，…,xn]T为D维决策向量，fi∶RD→R,i=1,2,…,k为第k个目标函数。多目标优化问题的多个目标间往往存在冲突，不同于单目标优化问题的单个最优解，多目标优化问题的最优解不唯一，得到的通常为一组均衡解，称之为Pareto解集。解集中的每个解称为Pareto解或非劣解，没有一个解的所有目标好于另一个解，由所有Pareto解的目标函数值构成的目标空间内的曲面称为Pareto前沿或Pareto面。在实际应用中，Pareto面使得决策者能够权衡不同的目标，从而选择出其所需的最终解。为此，寻找一种有效的方法以找出尽可能多的目标解受到了学者们越来越多的关注。

近年来，进化算法和群智能算法的提出为多目标优化问题提供了一种新的求解方式。由于他们实现简单，具有较好的收敛性，且这些算法基于群体优化，所获的是一组非劣解，从而越来越多的应用于多目标优化问题的求解[1-7]。然而，随着多目标优化问题应用领域的扩大，其目标函数越来越复杂，导致对解的一次评价需要大量的时间花费，大大阻碍了进化算法和群智能算法在多目标优化问题中的应用，这是因为无论是进化算法还是群智能算法，它们都是基于种群的迭代优化算法，任意一代都需要大量的适应值评价。为了进一步扩大进化算法和群智能优化算法的应用范围，学者们提出了使用适应值计算廉价的估值模型来替代适应值计算费事的实际目标函数计算，从而减少算法的运行时间。Lius VSantana-Quintero等[2]提出了将支持向量机(SVM)引入到多目标微粒群算法中；Zenghui Wang和Yanxia Sun[3]将多目标微粒群算法与BP神经网络进行结合；Bryan Glaze[4]等用多个代理模型相结合有效的解决了直升飞机旋翼的叶片减震问题。适应值继承是一类特殊的估值模型，1995年Smith等[5]第一次提出将适应值继承策略引入遗传算法中，其概念简单，实现方便，且保持了结果的较优性。2005年，Margarita Reyes-sierra和 Coello CoelloCarlos A[6]将适应值继承的概念引入到了多目标微粒群算法。2013年，Sun等[7]利用微粒群算法本身进化公式提出了一种进化估值策略，与一般的适应值继承策略不同，该估值策略除使用父代个体信息外，还使用同一代其它个体适应值信息来估计当前个体的适应值，单目标函数中的测试结果表明进化估值策略可以在较少适应值评价次数下获得问题的较好最优解。因此本文将进化估值策略进行扩展，使其能够应用于复杂多目标优化问题的求解中，以减少多目标微粒群算法优化的计算花费。

本文首先对一般进化估值策略辅助的微粒群算法进行了简单介绍。然后对其进行扩展，并引入相似度控制机制以确定估值的个体。随后，通过对多目标测试函数的仿真实验验证本文提出的估值策略在多目标优化问题中的有效性。最后对本文进行总结和展望。

1进化估值策略辅助的微粒群算法

微粒群算法(Particle Swarm Optimization，PSO)是1995年由美国心理学家KennedyJ与电气工程师EberhartRC受鸟类的群智能行为启发，模拟鸟类觅食过程提出的一种典型的群智能优化算法[8-9]。由于其概念简单、控制参数少、易于实现且有一定的并行性等优点，微粒群算法自提出以来就受到广泛关注。

其基本更新公式可表示如下：

vi(t+1)=Vi(t)+c1r1(Pi(t)-Xi(t))+

c2r2(Pg(t)-Xi(t))

(2)

Xi(t+1)=Xi(t)+Vi(t+1)

(3)

其中，c1和c2为两个常量，分别表示认知系数和社会系数。r1和r2是两个由[0,1]均匀分布的随机数组成的对角阵。Pi=(pi1,pi2，…,piD)为粒子i的历史最优位置，Pg=(pi1,pi2，…,piD)为种群历史最优位置。

为解决复杂单目标优化问题，基于式(3)和(4)，Sun等提出了一种新的继承策略，新个体的适应值通过以下公式进行计算：

(4)

其中，

(5)

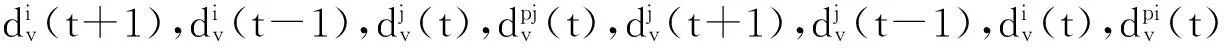
2进化估值策略辅助的多目标微粒群算法

本文拟将进化估值策略辅助的微粒群算法应用于复杂的多目标优化问题中，以进一步扩大微粒群算法的应用范围。

2.1多目标进化估值策略

不同于单目标优化问题，多目标优化问题得到是一组解，所以在个体进化过程中，其学习的群体最优位置往往不一样，因此，本文在引入虚拟位置时保留了群体历史最优位置，表示为：

Xv(t+1)=Xj(t+1)+(1+χ-χφ1-χφ2)Xi(t)+

(1+χ-χφ1′-χφ2′)Xj(t)+χXi(t-1)+

(6)

相应的，目标函数的估值公式修改为：

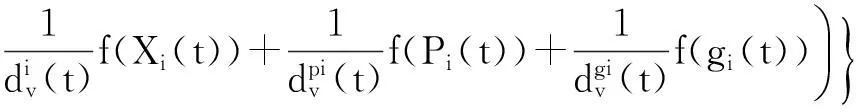
k=1,2,…,m

(7)

其中，

(8)

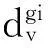
算法1给出了多目标进化估值策略的伪代码：

Begin

For 当前种群中每个粒子i

fitness(Xi(t+1)).evaluation=0;

fitness(Xi(t+1)).estimation=0;

End For

For 当前种群中每个粒子i

If fitness(Xi(t+1)).evaluation=0 and

fitness(Xi(t+1)).estimation=0 then

实际计算粒子i的适应值；

fitness(Xi(t+1)).evaluation=1;

End If

For 除i外的其他粒子k

IfXk(t+1)=Xi(t+1)then

将粒子i的适应值和评价及估计标志信息直接赋值给粒子k；

End If

计算粒子k与粒子i间的欧式距离，搜索粒子i距离最近的粒子j；

If fitness(Xj(t+1)).evaluation=0 then

If 以上10个距离均不为0 then

利用式(7)计算粒子j的适应值

fi(Xj(t+1))；

If fitness(Xi(t+1)).estimation=1 and

新解支配原解then；

f(Xj(t+1))=fi(Xj(t+1));

End If

End If

End If

End For

更新群体中粒子i的个体历史最优解集并排序；

End For

更新种群历史最优解集；

搜索种群历史最优解集中的估计解并实际计算后与其他解重新比较；

End

需要注意的是，在基于进化估值策略的多目标微粒群算法中，粒子第一次迭代所得最优位置对应的适应值需全部计算，以获得粒子在第二代适应值估值时所用的祖代信息。

2.2相似度评价控制机制

为了保证估值尽可能准确的前提下进一步减少目标函数的实际计算次数，与文献[10]中类似，本文引入相似度评价。对于任意粒子i与粒子j的相似度可由下式得出：

(9)

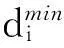
评价控制机制的作用是选择当前种群中可以通过估值公式估计适应值的粒子，加入相似度的评价控制机制即将多目标进化估值策略伪代码步骤“计算粒子k与粒子i间的欧式距离”及“找到与粒子i距离最近的粒子j(距离为0的粒子除外)”进行修改为“计算粒子k与粒子i间的相似度”及“找到满足相似度阈值的粒子j”.

2.3算法实现

算法2给出了本文进化估值策略辅助的多目标微粒群算法的伪代码：

Begin

设置参数，t=0，超立方体初始化种群；

实际计算种群中各粒子适应值；

将个体历史最优解集据小生境拥挤度排序存储到archive1；

将群体历史最优解集据拥挤度距离排序存储到archive2；

While 不满足停止条件 do

For种群中每个粒子i

从archive1和archive2中分别选出pbesti和gbesti引导粒子i的进化；

更新粒子的速度及位置；

将范围外的粒子拉回到搜索空间；

Ift=1

实际计算种群中所有粒子的适应值；

Else

带有相似度的多目标进化估值策略；

End If

End For

End While

选择外部存储空间内非劣解集作为Pareto最优集；

End

可以看出，算法中引入了超立方体初始化以提高算法的搜索性能，并设定了两个外部存储空间分别存储粒子的局部最优解集合种群的全局最优解集。在粒子进行位置更新前，对每个粒子的局部非劣解根据小生境[11]拥挤度排序，全局最优解根据拥挤距离[12]排序，分别选取其中较好解对应位置进行粒子的位置更新操作。若新位置超出粒子的搜索范围则在搜索空间内随机产生一个新位置，以提高种群的多样性。此外，为了减少算法中外部存储空间计算复杂度，本文利用基于拥挤度对存储空间大小进行了限制。

3仿真与分析

为了验证进化估值策略辅助的多目标微粒群算法的有效性，本文在5个2目标标准测试函数(ZDT1，ZDT2，ZDT3，ZDT4和ZDT6)[13]和2个3目标标准测试函数(DTLZ2以及DTLZ6)[14]上进行了测试，并和多目标遗传算法，多目标微粒群算法在趋近度(Generation Distance，GD)[15]，分布性(Spacing，SP)[16]和错误率(Error Rate，ER)[15]上进行了对比和分析。

实验中测试函数的参数设置如表1.

微粒群算法中种群大小为100，认知系数和社会系数c1=c2=2.05，收敛因子χ=0.798，程序独立运行30次，外部存储空间大小设置为100.ZDT1到ZDT6其每次运行最大迭代数为100，DTLZ2和DTLZ6的最大迭代次数为200.

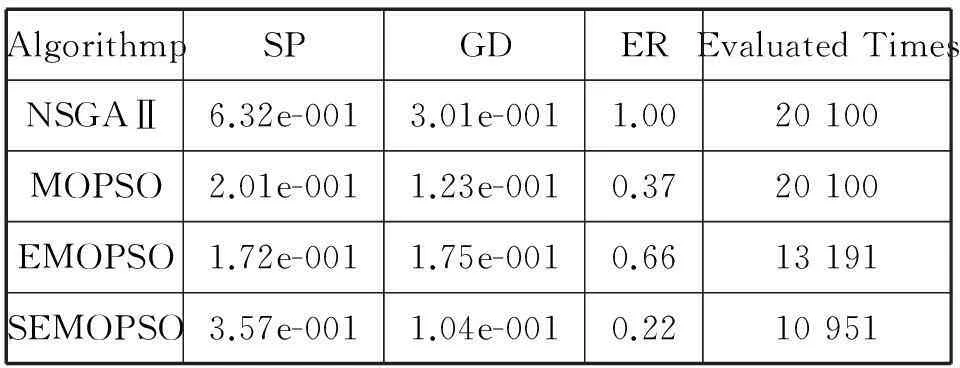
表2给出了不同算法在这些测试函数上的对比结果。其中“Evaluated times”表示算法迭代100次适应值实际计算次数即适应值的评价次数。

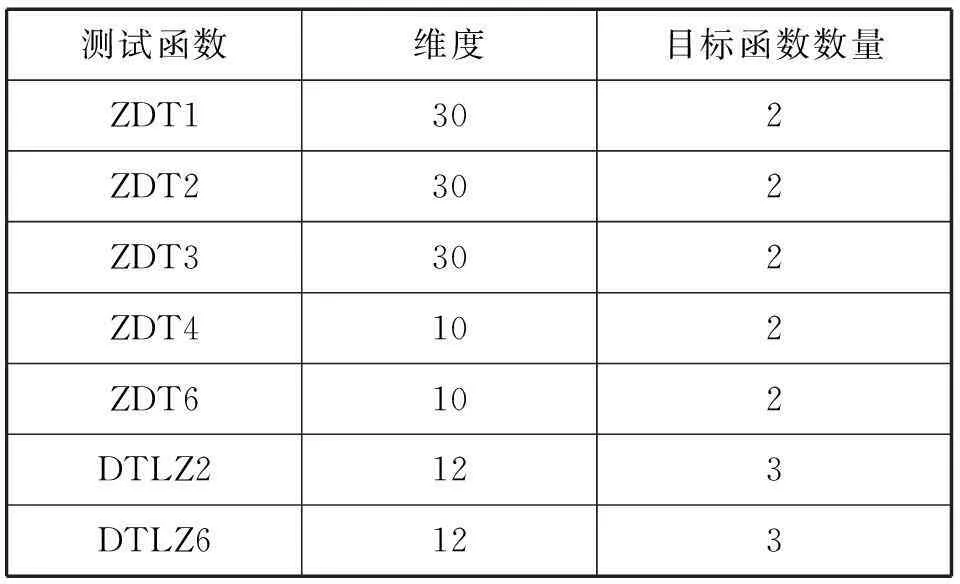
表1　测试函数相应参数

表2　多目标进化估值算法的对比实验结果

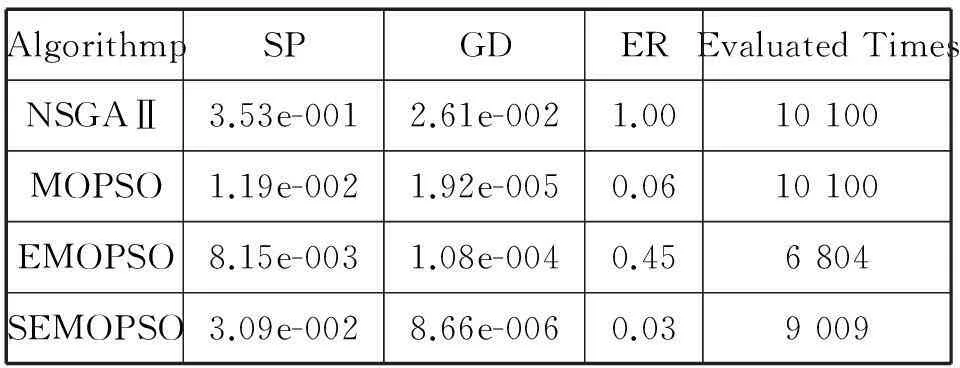
(b)ZDT2结果对比

(c)ZDT3结果对比

(d)ZDT4结果对比

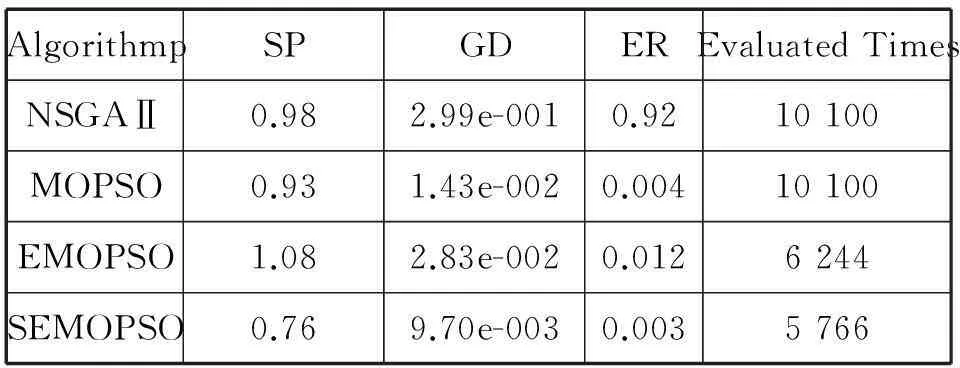
(e)ZDT6结果对比

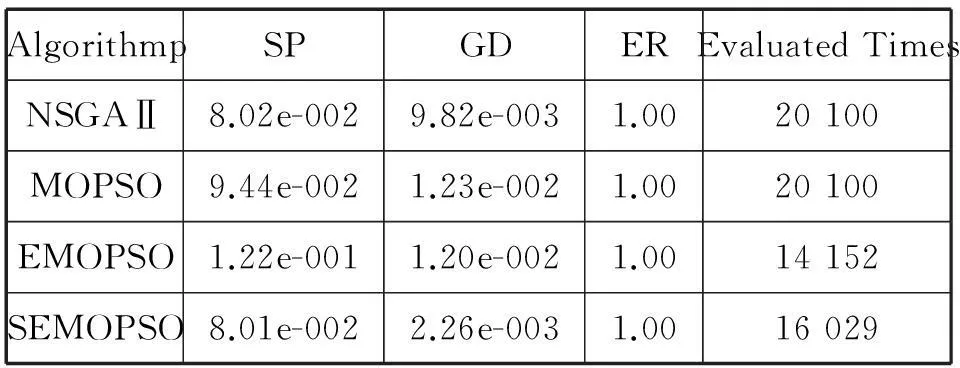
(f)DTLZ2结果对比

(g)DTLZ6结果对比

由表2可以看出，与NSGAⅡ和MOPSO相比，在相同迭代次数下，增加了估值策略的EMOPSO和SEMOPSO的适应值评价次数明显减少。从错误率和趋近度来看，本文的SEMOPSO算法除了ZDT4均获得了比其它算法更好的结果。分析其原因，ZDT4存在219个局部极值，而微粒群算法本身存在易早熟收敛的问题，因此在该问题上微粒群算法所求的解集与真实Pareto解集存在的差异较大。另一方面，具有估值策略的微粒群算法比无估值策略的微粒群算法具有更好的分布性。

为了更详细的查看算法优化过程中非劣解集的变化，图1给出了NSGAⅡ，MOPSO，EMOPSO和SEMOPSO四种算法对ZDT函数和DTLZ函数优化过程中每次迭代所得非劣解集各项评价标准在适应值实际计算次数下的变化曲线，以及评价次数随迭代次数变化曲线。由于各算法对函数ZDT4和DTLZ2函数优化所得最优解集错误率均为1，故图中未给出两函数错误率变化曲线。

由图1可知，进化估值策略的引入在算法的运行初期就有效的影响了非劣解集，尤其是当加入相似度的评价控制机制，函数的收敛曲线均在评价次数为1 000时即超过其他算法迅速收敛，最终趋于平稳。在对搜索空间单一的ZDT1和ZDT2优化时，EMOPSO所得非劣解集的分布性随着适应值评价次数的增加迅速减小，并很快超过其他算法并逐渐趋于平稳，然而其收敛性变化相对平缓且最终比SEMOPSO差。说明了在一些多目标优化问题中，解集分布性的提高通常会减慢算法的收敛速度造成解的质量与收敛速度间的冲突[17]。由图中各函数适应值评价次数随迭代次数变化曲线可知， 在优化初期三种算法的适应值估值次数均随着迭代次数以一定比值线性增加，SEMOPSO和MOPSO及NSGAⅡ的稍小一点，而EMOPSO的比值则远小于其他算法。在随后的优化过程中EMOPSO保持线性增长的趋势，而SEMOPSO的适应值曲线逐渐趋于平缓，甚至如ZDT6的适应值评价次数变化曲线所示，最终超过EMOPSO的变化曲线，得到最少的适应值评价次数。证实了，进化估值策略可以有效减少适应值实际评价次数，相似度可以提高适应值估值准确性的推断。

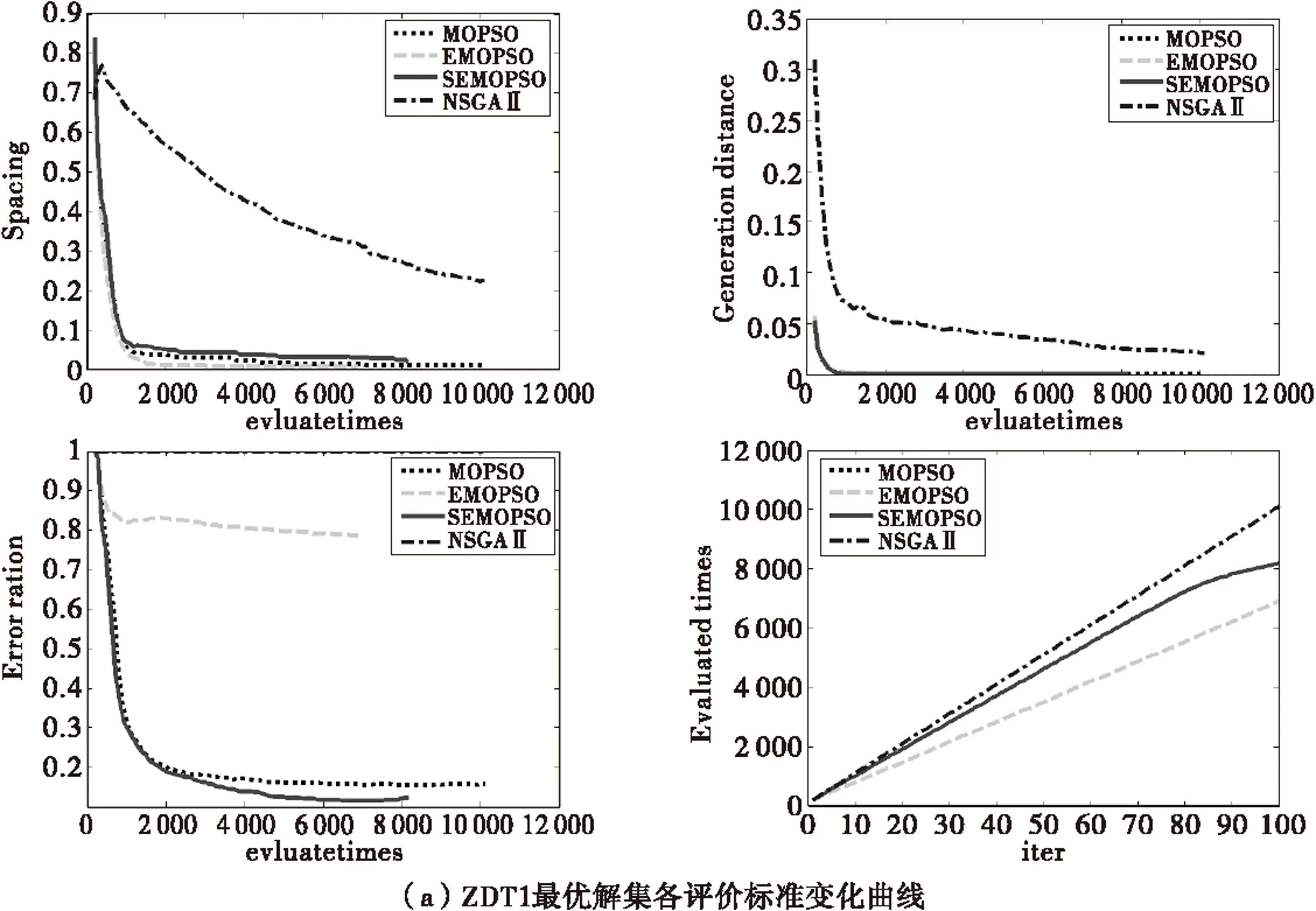
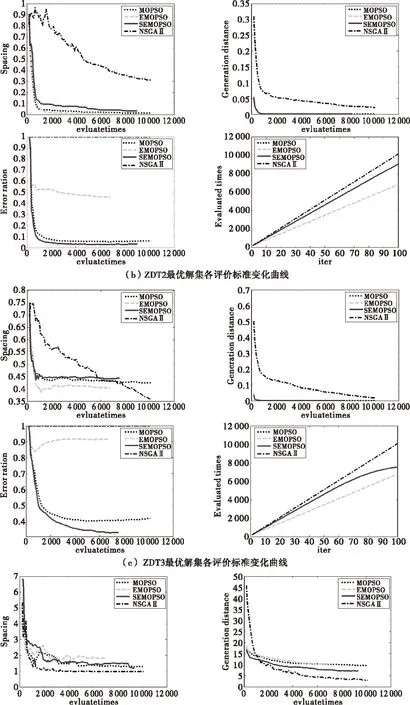
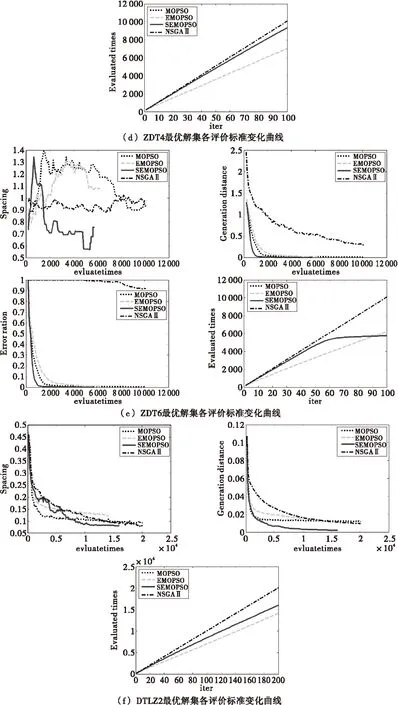
图1　NSGAⅡ，MOPSO，EMOPSO，SEMOPSO对测试函数优化所得最优解集各评价标准变化曲线

本文所选ZDT函数包含了一般两目标优化问题的所有特性，两个三目标DTLZ函数分别有连续的最优解集前沿和离散的最优解集前沿，较全面的测试了本文所提出算法的性能。由以上四种多目标函数所得最优解集的各个性能评价指标的对比实验结果可以得到以下结论：(1)在多目标的微粒群算法中，进化估值策略的引入可以明显减少适应值的评价次数。在用微粒群算法解决多目标的计算费时问题时，引入进化估值策略可以通过估值代替适应值评价，减少适应值评价次数从而减少算法的优化计算总花费。(2)相似度的评价控制机制可以提高估值的准确性，明显的提高算法的优化性能。加入相似度的进化估值策略的引入可以使算法在减少评价次数的同时提高优化性能，避免了估值的不准确性带来的影响。(3)进化估值策略在算法的整个优化过程中都发挥着作用，并且无论对于两目标的优化问题，还是多目标的优化问题，进化估值策略的引入都可以有效提高算法的性能减少算法的适应值评价次数。

4结束语

本文提出了一种多目标微粒群算法的进化估值策略，通过在多目标的微粒群算法中引入进化估值策略，以估值代替适应值的评价从而减少适应值的评价次数。进化估值策略中通过微粒群算法的更新公式推导所得估计公式，利用粒子的祖代父代以及同代已知适应值的粒子估计其适应值，代替目标函数的适应值计算。在进化估值策略中引入相似度的评价控制机制，利用粒子间的相似度选择所要估计的粒子。仿真实验表明进化估值策略的引入明显减少了算法优化过程中的适应值评价次数，而且在一定程度上增加了种群的多样性。相似度的评价控制机制的引入提高了估值的准确性，使进化估值策略在减少算法适应值评价次数的同时提高了算法的性能。多目标微粒群算法中进化估值策略的加入是有效可行的。

参考文献：

[1]苏长慧，夏桂梅.基于改进微粒群算法的单点信控交叉口配时优化[J].太原科技大学学报，2014，35(3)：198-201.

[2]SANTANA-QUINTEROLUIS V，COELLO COELLO CARLOS A，JESUS MOISES OSORIO VELAZQUEZ，et al.Surrogate-based Multi-objective Particle Swarm Optimization[C]∥Swarm Intelligence Symposium，St.LOuis，MO，2008：1-8.

[3]ZENGHUI WANG，YANXIA SUN.Fully Connected Muti-Objective Particle SwarmOptimizer Based on Neural Network[C]∥ICIC 2011，Springer-Verlag Berlin Heidelberg，2011：170-177.

[4]BRYAN GLAZ，TUSHAR GOEL，LI LIU，et al.Friedmann and Raphael T.Haftka.Multiple-Surrogate Approach to Helicopter Rotor Blade Vibration Reduction[J].Aiaa Journal，2009，47(1)：271-282.

[5]SMITH R E，DIKE B A，STEGMANN S A.Fitness inheritance in genetic algorithm[C]∥ACM Symposium on Applied Computing，NY，USA，1995：345-350.

[6]MARGARITA REYES-SIERRA ，COELLO COELLOCARLOS A.Fitness inheritance inmulti-objective particle swarm optimization[C]∥Swarm Intelligence Symposium，SIS 2005，Palathingal，USA，2005：116-123.

[7]SUN C，ZENG J，PAN J，et al.A new fitness estimation strategy for particle swarm optimization[J].Information Sciences，2013，221：355-370.

[8]KENNEDY J，EBERHARD R C.Particle Swarm Optimization[C]∥Proceeding of the IEEE International Conference on Neural Networks，Perth，Australia，1995：1942-1948.

[9]EBERHART R，KENNEDY J.A new optimizer using particle swarm theory[C]∥Proceeding of the Sixth International Symposium on Micro Machine and HumanScience，Nagoya，Japan，1995：39-43.

[10]SUN C，ZENG J，PAN J，et al.Similarity-based evolution control for fitness estimation in particle swarm optimization[C].IEEE Symposium on Computational Intelligence in Dynamic and Uncertain Environment(CIDUE)，2013：1-8.

[11]MARGARITA REYES-SIERRA，COELLO COELLOCARLOS A.Multi-objective Particle SwarmOptimizes：A Survey of the State-of- the-Art [J].International Journal of Computational Intelligence Research，2006，2(3)：287-308.

[12]DEB K，AGRAWAL S，MEYARIVAN T.A Fast Elitist NonDominatedSorting Genetic Algorithm for Multi-Objective Optimization：NSGA-II[C]∥Proceedings of Parallel Problem Solving from Nature - PPSN VI，Paris，England，2000：849-858.

[13]ECKART ZITZLER，KALYANMOY DEB，LOTHAR THIELE.Comparison of MultiobjectiveEvolutionary Algorithms：Empirical Results[C]//Evolutionary Computation，SanDiego，USA，2000，8(2)：173-195.

[14]DEB K，THIELE L，LAUMANNS M，et al.Scalable multi-objective optimization test problems[C]∥Proceedings of the Congress on Evolutionary Computation，Honolulu，USA，2002：825-830.

[15]VAN VELDHUIZEN DA，LAMONT G B.Multiobjective evolutionary algorithm testsuites[C]∥Proceedings of the 1999 ACM Symposium on Applied Computing，Texas，USA，1999：351-357.

[16]TAO ZHANG，TIESONG HU，YUE ZHENG，et al.An Improved Particle Swarm Optimization for Solving Bilevel Multiobjective Programming Problem[J].Journal of Applied Mathematics，2012，30：1-13.

[17]YEN G G，LU H.Dynamic multiobjective evolutionary algorithm：Adaptive cell-based rank and density estimation[J].IEEE Transaction on Evolutionary Computation，2003，7(3)：253-274.

Fitness Estimation Strategy Assisted with Particle Swarm Optimization for

Complicated Multi-objective Optimization Problem

LIU Tong，SUN Chao-li，ZENG Jian-chao

(Complex System and Computational Intelligence Laboratory，Taiyuan University of Science and Technology，

Taiyuan 030024，China)

Abstract：As a swarm intelligence algorithm，particle swarm optimization needs a lot of fitness evaluation before locating near to global optima， which impedes it to be applied in the complex multi-objective problems. In order to

solve the problem，an evolutionary fitness estimation strategy is proposed，in which the real fitness evaluation will be replaced by fitness approximation，so that the number of real computationally expensive fitness evaluation will be reduced and the computation expense will be correspondingly saved.The experimental results showed that evolutionary fitness estimation strategy assisted with multi-objective particle swarm optimization can reduce the times of fitness evaluation，and evolutionary fitness estimation strategy with similarity can improve the correctness of fitness approximation so as to improve the optimization performance and reduce the times of fitness evaluation.

Key words：multi-objective particle swarm optimization，fitness estimation strategy，similarity，fitness evaluation