2012年4月11日M8.6印度洋地震的深远影响：短期全球触发后为更长期全球阴影

Fred F.Pollitz Roland Bürgmann Ross S.Stein Volkan Sevilgen

0 引言

2012年4月11日M8.6地震是大洋岩石层中发生的一次异常大的走滑型事件（McGuire and Beroza，2012）。在这次地震之后的几天中，全球4.5≤M≤7.0的地震活动率增加了（Pollitz et al，2012）。全球地震活动发生率的显著变化分别发生在主震前和主震后的6天内，以及相对于背景发生率的量度（Pollitz et al，2012）。我们将M≥6.5的地震标绘在图1d，图中显示相对于主震前3个100天内的地震发生率（平均约为0.1个地震／天），主震后的地震活动率表现为短暂升高（10天中为0.4个地震／天）。

虽然其他特大地震触发过全球的小地震和颤动，但通常根据地震波的通道（例如，Prejean et al，2004；Velasco et al，2008；Gonzales－Huizar et al，2012），此次印度洋地震所引起的全球地震活动响应则是独一无二的。这种地震活动响应可以达到大震级（最大可达到7.0级），而且主要是延迟触发的地震活动。这可能与高应力降以及与该地震事件相关联的勒夫波激发有关（McGuire and Beroza，2012；Meng et al，2012；Yue et al，2012），但仍有许多有待解释的地方，尤其是延迟触发的机制。

这次地震的特别之处还体现在另一个方面。这次地震发生以后，全球M≥6.5地震活动在经过一个短暂的加速之后，进入了一个近100天的平静期（图1e）。我们将证明如此长时间都没有大地震发生是非常罕见的。这就出现了与2012年4月主震有关的问题，特别是主震所引起的在全球传播的地震波是否不仅能产生短暂的加速期，而且也能产生一个更长期的平静期。

2012年4月地震事件触发力的一条线索是阿拉斯加M3.9动态触发余震之前约20s的前震系列视触发（Tape et al，2013）。这表明在产生一个更大的触发地震之前，接近破裂的震源片区可能会出现逐渐的前兆滑移。这支持一种延迟动态触发的模型，其中慢滑动或小地震会导致更大的触发地震（Peng and Gomberg，2010；Shelly et al，2011）。我们认为这种模型的变化形式为：通过地震波的传播，接近破裂的震源区域处于更接近破裂的状态，使很大的区域应力高出阈值。为了解释随后约100天中M≥6.5地震活动停止出现的原因，这个模型进一步假定了一个动态阴影效应，当许多震源区接近破裂和预期要破裂时，它可抑制地震活动。

在本研究中，我们证明了2012年4月印度洋地震事件之后有短期（10天）的地震活动增加期和更长期（随后的95天）的地震活动平静期。我们应当明确的是：就主震之后长期全球地震活动的缺乏而言，在过去一个世纪的大主震中，2012年发生的主震是非常独特的。这就促使对其物理意义进行讨论。尽管基于任一特定观测的模型都是推测的，但我们将提出全球断层系的简单模型。这个模型将同时作为合理地说明2012年主震后地震活动模式，以及突出是什么使得这次大型主震与之前的许多其他地震不同的参考。

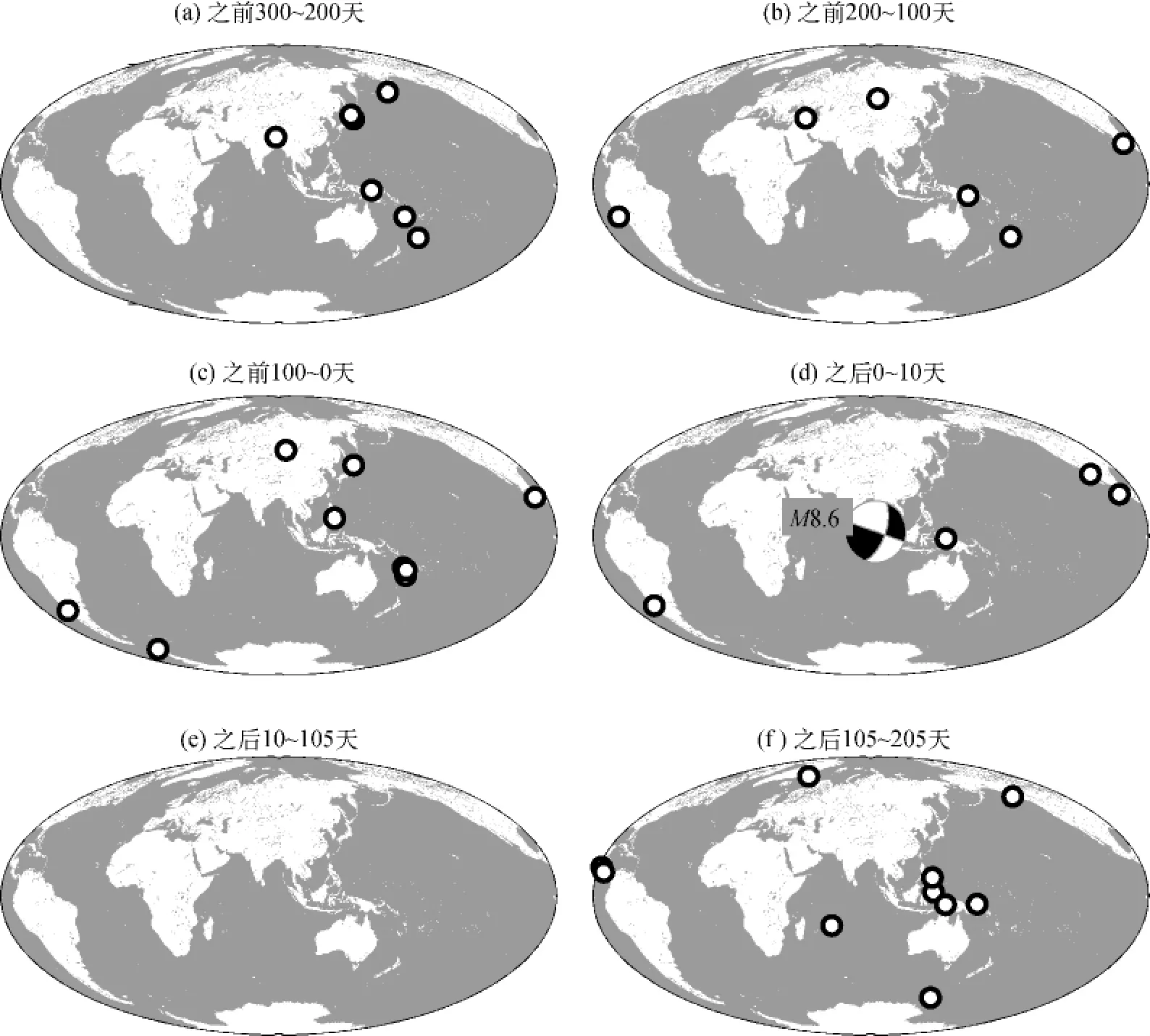
图1 在所示时段遥远的全球M≥6.5地震活动（此图及后续的图中深度为0～100km）。时间以2012年4月11日印度洋地震的发震时刻为准。遥远地震是指距离2012年4月11日印度洋地震震中大于1 500km的地震事件（如图d所示）

1 主震之后的加速

我们使用国家地震信息中心（NEIC）的地震目录来说明2012年4月11日主震前后的全球地震活动模式。我们利用已公布的矩震级MW。Politz等（2012；他们的图S3）发现，从2002年到2012年，这个地震目录的完整震级Mc约为4.8。使用自2009年以后的地震目录事件进行类似分析说明Mc约为4.5。根据对国家地震信息中心地震目录与局部地震目录的比较，这与较小区域估计的Mc一致（例如，Goslin et al，2012；Sevilgen et al，2012）。

图2表示未经编辑的目录中4.2年时段内全球M≥4.5地震的累积数。M≥4.5地震的累积数增加与M≥6.5地震的发生具有很好的相关性（在图2中分别用垂直虚线和空心圆表示，扩展到M≥6.4）。其中在2010年2月28日M8.8马乌莱地震、2011年3月11日M9.0日本东北地震和2012年4月11日M8.6印度洋地震发生时的增长现象特别明显。我们也使用从最大主震去掉局部余震的去丛集目录来评估类似的地震活动。该全球地震目录在编辑时，将发生在M≥8.0地震之后1年之内且距该地震1 500km范围以内的所有M＜8.0地震去掉。我们称此为大主震去丛集。图3显示了全球M≥4.5地震的累积数和M≥6.5地震的发生时间。去丛集去掉了马乌莱大地震、日本东北大地震和印度洋大地震（及所有其他M≥8.0主震）的局部余震。然而，不管该目录如何编辑，可见印度洋地震之后M≥6.5的地震均是增加的（例如，这些图的b图），这是因为这些较大地震都很遥远。

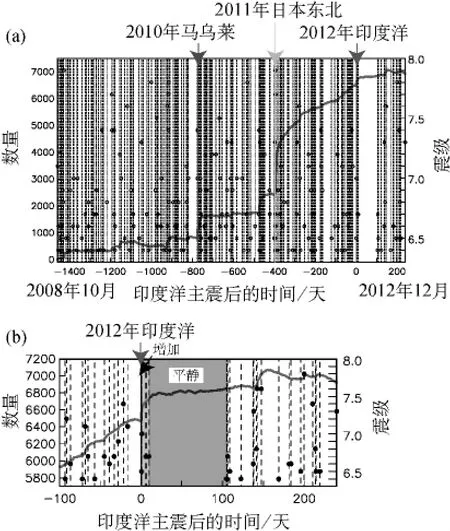
图2 （a）减少13个地震／天的M≥4.5地震的累积数。时间以2012年4月11日印度洋地震的发震时刻为准。垂直虚线表示M≥6.4地震的发生时间，空心圆表示震级。使用的地震目录未经编辑（即没有1 500km禁区）。图（b）是图（a）在主震前100天到主震后240天的特写图。此图的彩色版仅适用于电子版本

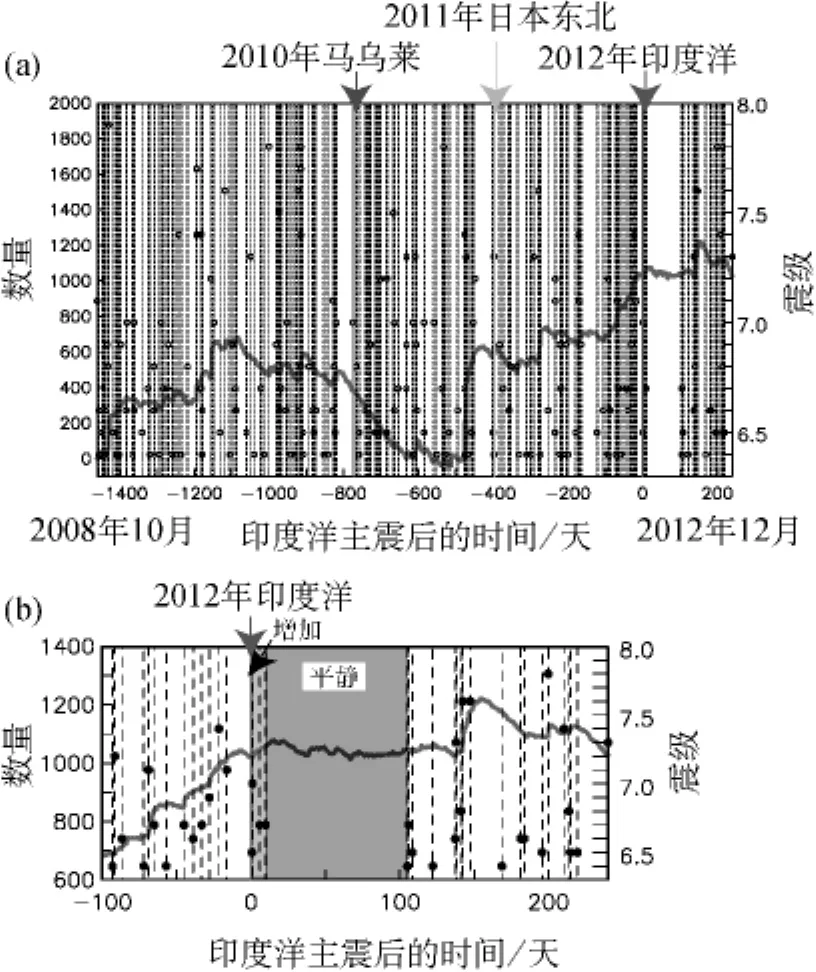
图3 （a）减少13个地震／天的M≥4.5地震累积数。时间以2012年4月11日印度洋地震的发震时刻为准。垂直虚线表示M≥6.4地震的发生时间，空心圆表示震级。地震事件经过大主震去丛集处理后编辑的。图（b）是图（a）在主震前100天到主震后240天的特写图。在2012年4月11日M8.6地震之前475天发生的大主震是2010年12月21日日本近海M7.4地震。由于此次M7.4地震在去丛集处理中没有被去掉，因此其后有剧烈的局部余震活动。此图的彩色版仅适用于电子版本

由Pollitz等（2012）确定的全球触发地震活动的诊断性是走滑地震占主导地位，这大概是因为在全球辐射的最强地震能量都由勒夫波传输，对于动态触发的走滑地震具有较高的潜力（Hill，2010）。图4a，b给出了由全球矩心矩张量目录（全球矩心矩张量项目，见数据与来源；Dziewonski et al，1981；Ekströmet al，2012）得到的累积到时t为止在M≥5.0遥远地震的总数中走滑型震源机制的M≥5.0遥远地震的分数γ（t）。另外，用于构建γ（t）的走滑型地震和所有地震的发生时间分别在图4c和图4d中给出。在2012年4月11日主震之后的几天中，γ（t）值显然高于由震前几年确定的0.24的背景值。图4中还包含从2012年4月11日主震之后的累积走滑型地震数计算出的γ（t）图像。与主震后的γ（t）图像相反，主震前的γ（t）图像在背景值上下波动，与延长期的值没有系统差异。

根据发生率的变化和由震后两天得到的绝对发生率，可以推断出全球M≥5.5的遥远地震活动99%均升高了（Pollitz et al，2012）。这种M≥5.5的异常地震活动发生率在主震之后持续了10天。这是通过将震后10天观测到的地震活动率增加与2012年4月地震之前20年内所有M≥7.0主震后10天的经验概率分布进行比较得到的。图5表明，观测到的地震活动率超过了震级阈值5.5和更大的经验概率分布95%以上。

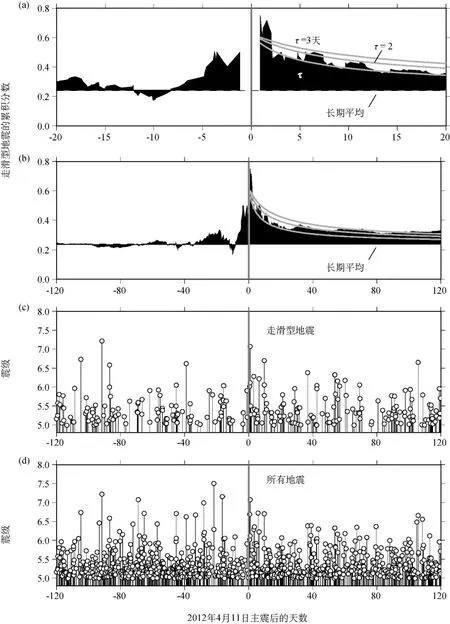
图4 （a，b）在2012年主震前和主震后分离时段计算的M≥5.0走滑型地震（在图上用与中性轴大于60°的线表示）相对于全球地震总数的时间平均累积分数。图（a）是图（b）20天时段的特写图。灰色表示通过公式（4）取值A＝10、τ＝1，2，3天得到的全球走滑型地震的大森衰减模型曲线。主震前的累积曲线是对2012年4月11日地震之前的时间计数得到的（用垂直粗灰线表示）。下面的图给出地震的发生时间和震级，其中（c）为该时段内M≥5.0的地震结果，（d）为所有地震的结果。所有地震都约束在离2012年4月11日地震震中1 500km以外。该图中的所有数据均取自全球矩心矩张量目录

图5 M≥7.0主震之后10天期间给定震级以上遥远地震活动发生率的经验概率密度函数。这是使用Pollitz等（2012）文中方法一节所述的采样程序计算的结果，且使用了2012年4月印度洋地震之前20年发生的243个M≥7.0主震。所有地震活动率在给定M≥7.0主震之后发生的地震均约束在以该主震为中心半径为1 500km的圆形空区之外的意义上都是遥远的。虚线表示分布的5%和95%的尾部，垂直灰线表示2012年4月地震之后10天观测的遥远地震活动率

2 触发到背景地震活动的过渡

2012年主震之后的加速很短暂，我们接下来的目的是对到背景地震活动过渡的量化。在图4中，含时间的γ表现为大森形衰减关系。我们对此用模型进行解释，其中全球走滑型地震的发生率为：

式中，r0是全球M≥5.0走滑型地震的背景活动率，A和τ为常数。发生在主震后的走滑型地震，截止到t时间的累积数为：

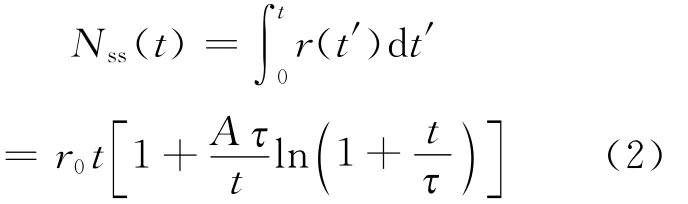
设Ntotal（t）为主震后0到t时间内M≥5.0遥远地震的累积总数。如果我们粗略地假设大部分主震后的加速都是由于走滑型地震优先触发的，则有：

这就得出了γ的表达式：

图4a，b中的灰色曲线是用方程（4）以A＝10、τ＝1，2或3天预测的结果。对观测γ值的拟合说明，增加的全球走滑型地震活动随大森时间常数τ≈1～2天衰减，与2012年主震之后几天内触发地震到背景地震的逐渐过渡相吻合。然而，尽管这告诉了我们触发遥远地震持续了多久，但却未完整描述地震发生率的过渡，这在下两节所述方法中震级是关键。

3 主震后的平静

2012年4月11日主震之后全球地震发生率的初始加速（图1d），包括高达M7.0的大震级的地震活动是很不寻常的。其中，在2012年4月21日到7月26日的随后95天期间，M≥6.5地震活动的平静更是不同寻常（图1e）。通过与主震前3个100天和主震后100天的地震活动进行比较，这种模式更加明显（图1a，b，c，f）。另外，这种模式在图2和图3所示2008～2012年期间的M≥6.5地震事件中也有体现，这里使用的是未经编辑的目录数据或未经大主震去丛集的数据。相对于可能的局部余震，看到的95天的周期是比较可靠的：即使在未经任何目录编辑的情况下对全球地震活动率进行评估，这个周期仍然是可靠的。

全球地震活动停止的类似观点在图6中也有说明，其中给出了使用经大主震去丛集的国家地震信息中心地震目录得到的M≥6.5地震的累积数。斜率为0.089个地震／天的实灰线代表30年的背景地震活动率。如果将这个活动率外推到主震后的105天，那么在这段时间内就应该有9.4个M≥6.5的地震发生；只发生了4个（发生在震后的10天内），留下5.4个地震的明显空缺。这个空缺相当于全球M≥6.5地震60天的活动。

为了探讨全球地震平静期发生的频度，我们使用了国际地震中心全球地震模型（ISC－GEM）的地震目录，它开始于1900年，计划用来取代之前的 《百年地震目录》（Engdahl and Villaseñor，2002）。该ISCGEM全球仪器记录地震目录（Storchàk et al，2012）对1900～2009年期间的19 000个地震进行了重定位，这是为改编、大幅扩充和校正现有文献数据而努力的结果。数以百万计的震相记录都已被数字化，且所有的地震都利用Bondár与Storchak（2011）的方法进行了重定位。近乎完整的记录是自1900年以来M≥7.50的地震，1918年以来M≥6.25的地震，以及1965年以来M≥5.50的地震。

对30年（1982～2012）的国家地震信息中心地震目录和ISC－GEM地震目录的分析表明，遥远的M≥6.5地震的背景发生率为：没有编辑处理的情况下为0.105个地震／天，经大主震去丛集处理的情况下为0.089个地震／天。使用后一个发生率值，并假设地震的发生为泊松分布，这意味着在95天内无M≥6.5地震发生的概率约为exp［－8.45］＝2×10－4。这么低的概率通过使用ISC－GEM地震目录中M≥6.5遥远地震之间的间隔时间ΔT证实了。为了更准确地表示M≥6.5遥远地震的发生，并减少在较短ΔT时间内任何可能的偏差，我们进行了大主震去丛集。图7显示在过去的一个世纪中，仅有3个实例中地震间的间隔长于95天。ΔT超过95天的概率在过去的95年为0.0012（图7a），在过去的59年为0.0011（图7b）。

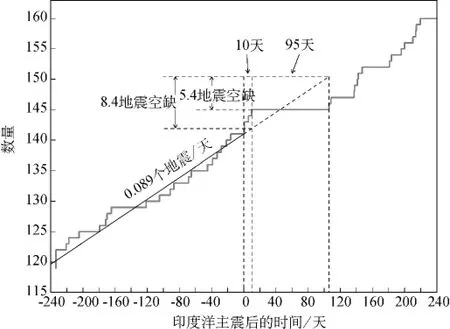
图6 用大主震去丛集后的国家地震信息中心地震目录得到的2012年4月印度洋主震之前240天到之后240天M≥6.5地震的累积数（未去丛集的图形几乎相同，只多3个地震）。尽管检查主震后105天内预期发生M≥6.5地震的预算时可明显见一个5.4地震的空缺，但由于动态触发而在最初10天之内发生的4个地震对这一时段预期M≥6.5地震发生率的预算没有多少贡献。这在95天平静期产生了有效的8.4地震空缺。0.089个地震／天的背景发生率基于的是30年的国家地震信息中心地震目录和ISC－GEM地震目录

上述ΔT＞95天的经验概率是基于对所观测到的地震平静期的回顾性分析得到的。当现实中该现象在足够长的观察时间内势必会出现时，回顾性分析可以使这种现象显著出现（例如shearer and Stark，2011）。在当前的情况下，过去一个世纪中几次观测到ΔT长达100天，的确使得单次观测到的这种间隔不一定显著。但这种观测的重要性在于它发生在一次非常大的地震之后仅几天。为了从整体上来看这些现象，我们检查了自上次大主震之后M≥6.5地震之间间隔时间ΔT的模式（即两个连续M≥6.5地震中第一个之前的主震），这里我们限制主震为M≥8.0的地震。每一对M≥6.5地震都可如图8a，b所示表示在以ΔT为一个轴，以自上次大主震后的消逝时间为另一个轴的图上。这种模式是通过大主震去丛集确定的，在历史地震目录中往往产生更长的ΔT，从而使得印度洋地震之后平静期的异常较少。图8c所示的这种模式揭示了ΔT与大地震后的消逝时间没有系统的关系。自上次大主震后的消逝时间大致服从均匀分布，并且消逝时间与长地震间隔时间之间没有物理联系。在非常大（M≥8.5）的地震事件中，2012年4月主震是非常独特的，因为它有超长的间隔时间ΔT和主震后较短（10天）的消逝时间。2012年4月主震与过去一个世纪中其他主震异常长的间隔时间在6.25的震级阈值也很明显（图8d），尽管它弱于更大的震级阈值，并且其他过去大主震发生后也伴有异常长的间隔时间ΔT（例如1964年阿拉斯加M9.3地震和1952年堪察加M8.9地震）。我们发现，当震级阈值为6.0时没有这种模式，表明观察到的现象仅限于M6.25以上的全球地震事件。

图7 用ISC－GEM地震目录得出的全球M≥6.5地震间隔时间ΔT的直方图：（a）1918年到2012年4月11日期间，（b）1950年到2012年4月11日期间。这里经过了大主震去丛集处理。图中还给出了每种情况下ΔT超过95天的概率

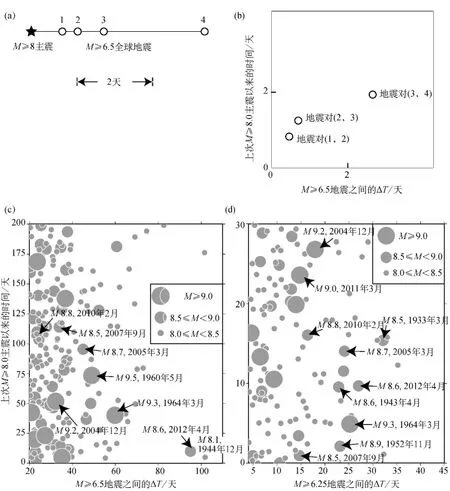
图8 （a）4个连续假想的M≥6.5地震及在它们之前最近的M≥8.0地震以示意性时间线的表示。（b）所得的3对连续M≥6.5地震以其间隔时间ΔT（横坐标）和给定对中从M≥8.0地震到第一个M≥6.5地震的时间（纵坐标）的表示。（c）M≥6.5地震和（d）M≥6.25地震的间隔时间ΔT随两个连续M≥6.5（或6.25）地震的第一个之前最近的M≥8.0主震后时间的变化。地震数据来自1918至2012年7月的ISC－GEM目录。经过了大主震去丛集。图上标出了过去显著大主震的数据；并标出了与特定主震最大ΔT相关的连续M≥6.5（或6.25）的地震对。在图（c）中，没有给出2011年3月日本东北地震的任何数据，这是因为日本东北地震后的ΔT没有超过下个全球M≥8.0主震发生前的20天。全球地震台站的报告在第二次世界大战期间极差，因此1944年发生的M8.1地震的ΔT可能低于图上所示的

具有类似大ΔT和短消逝时间的为1944年12月7日发生于南海海槽的M8.1东南海地震，在图8c中该地震的位置接近于本次2012年地震。在两次连续的M≥6.5地震之间有ΔT＝103天的空区，它们分别为1944年12月12日沿阿留申岛弧的M6.51地震和1945年3月23日沿太平洋南极岭的M6.83地震。尽管在此期间全球有4个M≥6.5的地震，但它们均在1944年12月7日主震1 500km范围以内，因此根据遥远的判据而将其去除了。然而，在这段时间期间，《百年地震目录》（Engdahl and Villaseñor，2002）中还有另外6个距1944年12月7日主震遥远、体波震级mb在6.6～7.2之间的地震。在ISC－GEM地震目录中，这些地震事件要么是标为震级MW小于6.5，要么是没有标出震级。这些另外的地震事件仍然需要进一步检查，因为mb会造成低估MW，尤其是震级较大时（Kanamori，1983）。因此，1944年12月7日地震明显大的ΔT可能是与二战期间地震事件监测误差有关的不确定MW赋值的人为结果。

从使用大主震去丛集的角度来看，我们发现当与其他地震事件进行比较时，应用它可以使得2012年主震的出现不那么显著。至于对未编辑地震目录的模拟，对M8.0的去丛集处理将图7中的地震间隔时间推到右边（即变得更高）。同样它也将图8中所有过去发生的大主震的间隔时间都推到右边。如果阈值较低（例如M7.5），就会使2012年主震更加突出。这是因为去丛集对2012年主震后的间隔时间没有影响。这一点在图2和图3中也已说明：即使使用未编辑的地震目录，地震平静期也会保持很长时间。同样，如果半径减小到1 000km，地震平静期也会保持，而且减小的半径会使图7和图8中的间隔时间往左移，从而使得2012年地震平静期出现得更明显。

4 震级—频度统计

我们希望将2012年4月发生的地震活动短期增长和更长期减少与遥远背景地震活动率进行比较。我们采用的是国家地震信息中心地震目录，遵循的是Pollitz等（2012）的方法，背景地震活动率是根据2012年4月印度洋主震前4年期间M≥8.0地震后所有10天间隔获取的；而每个M≥7地震的震中则为每个地震后10天内半径1 500km区域的中心。大主震的去丛集处理可以看作是附加滤波器的叠加，但是我们给出的背景活动率已经去除了大部分局部余震（这与下面定义的措施一致）。背景活动率在图9f中用实心圆符号表示。

2012年4月地震之后10天内发生的遥远地震，可以用离此次地震1 500km以外来进行约束。它们在图9f中用空心三角符号表示。与背景地震活动率相比，短期（主震后0～10天）的地震活动升高了。

我们评估了印度洋主震之后10～105天的全球地震活动，并去除了距此次主震震中1 500km以内的全部地震事件。对于M≥4.5的地震，印度洋主震后10～105天的地震活动率按照其震级—频度统计与背景活动率类似（图9f）。印度洋主震后10～105天期间，M≥6.0地震与背景不同，且缺乏M≥6.4地震。

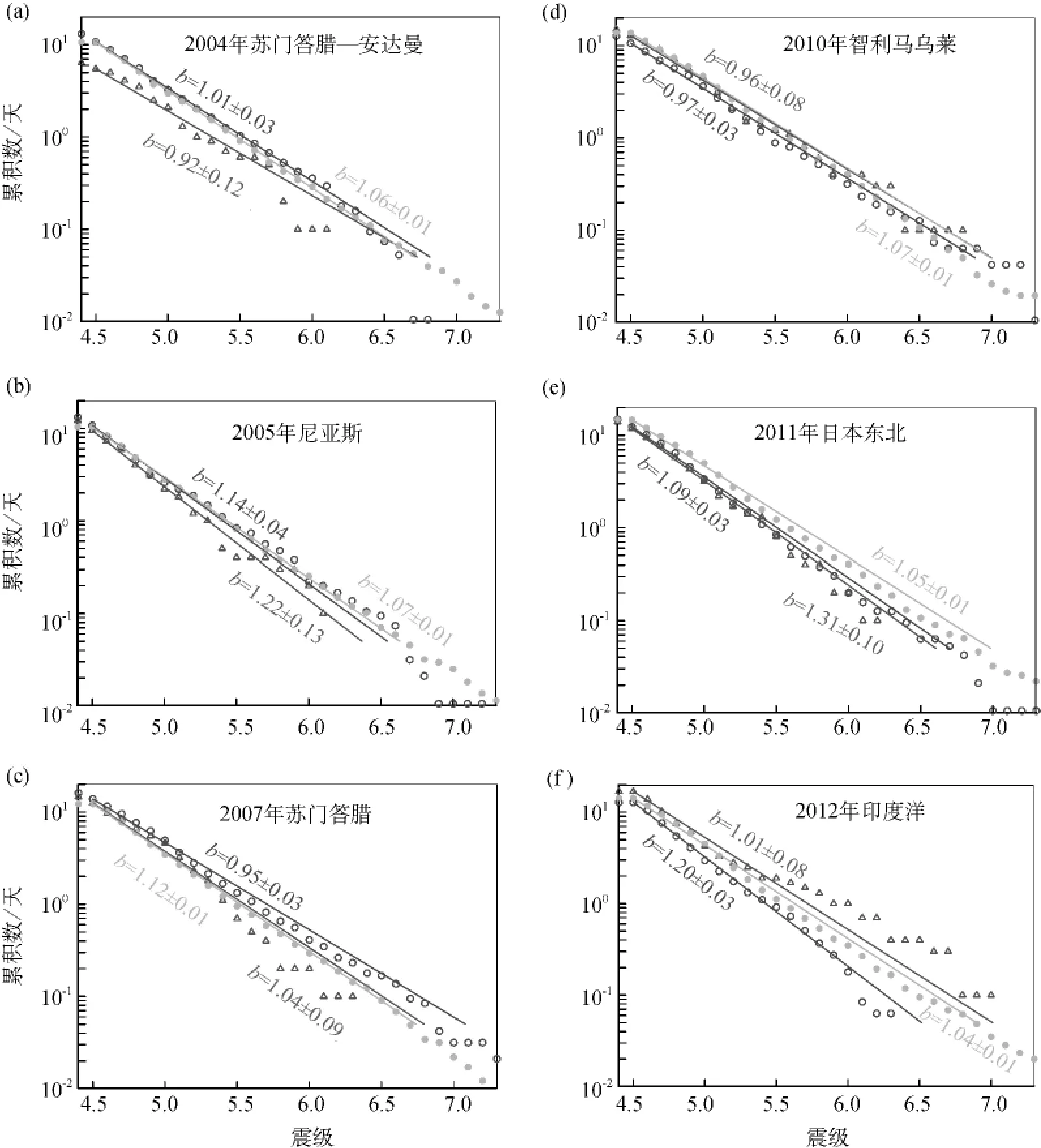
图9 使用国家地震信息中心地震目录归一化为所考虑时间间隔的遥远地震事件的累积数与震级大小的关系。实心圆代表使用给定主震前4年的地震活动计算的遥远背景地震事件。三角形代表给定主震后0～10天内的遥远地震事件。菱形符号代表给定主震后10～105天期间的遥远地震事件。斜直线表示用最大似然估计计算的b值对线性震级—频度关系的拟合。（a）2004年12月26日苏门答腊—安达曼M9.2地震；（b）2005年3月28日尼亚斯M8.7地震；（c）2007年12月12日苏门答腊M8.5地震；（d）2010年2月27日智利马乌莱M8.8地震；（e）2011年3月11日日本东北M9.0地震；（f）2012年4月11日印度洋M8.6地震。去掉了距每个相应主震1 500km以内的震中。此图的彩色版仅适用于电子版本

发生在过去10年的其他大主震（M≥8.5），也获得了类似的频度—震级统计结果：2004年苏门答腊—安达曼M9.2地震、2005年尼亚斯M8.7地震、2007年苏门答腊M8.5地震、2010年智利马乌莱M8.8地震，以及2011年日本东北M9.0地震。对2012年主震，使用了主震之前4年的背景活动率，和主震之后0～10天及10、105天的间隔时间，并去掉了至每个主震震中1 500km之内的地震。图9a－e给出的这些其他主震的结果既没显示出显著的短期活动率增加，也没显示有更长期的下降；更长期的地震活动率（图中用空心圆表示）一般不会在任何震级饱和，也就是说，不会有更长时间段的静止。图9a中显示出了2004年苏门答腊地震后M≥6.9地震的可能静止期。如何将其与2012年地震震后M≥6.5地震的平静期进行比较，也许可以如图7中M≥6.5地震所做的那样由ISC－GEM地震目录生成的M≥6.9遥远地震间隔时间ΔT的直方图来确定。我们发现，间隔时间ΔT＞95天的概率在1918～2012年和1950～2012年期间分别为0.035和0.032。这个概率约是M≥6.5地震间隔时间ΔT＞95天的30倍，因此2004年地震后的平静期远远不如2012年地震后的平静期显著。尽管常用主震后10～105天来检验所有情况下可能的下降，但这种模式相比于其他的选择（例如震后50～200天）更可靠。这也证实了由间隔时间统计（图8）给出的模式，即2012年主震在近期记录完整的大主震中是唯一的。

5 对地震物理学的推断

在附录中，我们研制了2012年地震激发的全球地震活动的统计模型。该模型涉及到几万个能发生M≥6.5地震破裂的震源片区、系统内每个断层的平稳加载，以及对完全应力降和临界应变阈值εcrit的近破裂之间应力状态随机分布的假设。这是为了解释全球M≥6.5地震活动率中10天的增长和随后95天的减少。这个模型得到的两个结果为：

1.由地震波致使瞬时应变大于εcrit的约6%的片区确实破裂了；

2.在没有破裂的片区中，有约88%的片区都会在100天内以某种方式从潜在破裂场地中去除，它们先前已接近破裂也是如此。

这种明显接近破裂的场地从M≥6.5地震就能破裂中去除是非常令人吃惊的，这有两种可能的解释：

1.主震瞬时应力可能改变了接近破裂片区的状态，并延缓正在进行的破裂过程；

2.渗透性的动态改变可能减少沿断层的有效应力，例如通过改变孔隙流体压力的分布和沿片区摩擦的有效系数。

第一种解释先前已经作为延迟触发的机制由Parsons（2005）提出，涉及到通过平均临界滑移距离Dc的增加由动态应力改变断层的状态。我们认为这是一种适用于延迟破裂的可能机制，即使破裂在不存在瞬时动态应力的情况下即将发生也如此。在速率—状态摩擦理论的情况下，Parsons（2005）发现尽管地震活动引起Dc的减少可能会发生（并导致地震活动率增加），但在物理上也合理的是动态应力会使Dc增加（并导致地震活动率降低）。

第二种解释基于的是断层往往具有由高渗透性损伤区包围的低渗透性核（Caine et al，1996）。瞬时应力可能会突然性地降低断层的渗透性，并暂时允许局部孔隙压力改变，这就可能触发地震（如Brodsky et al，2003）。然而初始扰动后的恢复过程将会起到降低断层带渗透性的作用（见Mangaet al，2012中的第4节）。尽管恢复过程被认为回复到了断层带预先存在的状态，但可以想象的是可能通过在初始扰动中排出断层带中的流体，断层带或许会经历有效应力的净减少。

所提出的两个过程的任何一个如果真正适用，就可以用2012年主震的动态应力来模拟，而不是用过去一个世纪中的任何先前大主震。同时它还会影响能产生M≥6.5地震破裂的初始震源区。与2012年主震有关的动态应力与其他任何历史地震事件的相当，其中，具有较大震级的地震，比如2004年苏门答腊M9.2地震，其动态应力更大（如Pollitz et al，2012中的图S－10）。这有可能是因为较之其他类似净地震矩的破裂，它有紧凑的破裂区域，因此破裂持续时间也短且应力降也高（McGuire and Beroza，2012；Meng et al，2012；Yue et al，2012）。另外，作为罕见的走滑型地震，2012年主震激发的主要是勒夫波而不是以很大主震占多数的逆冲地震产生的瑞利波。有人可能会提出，在模拟以上过程时，勒夫波比瑞利波更有效，尽管从小地震事件的动态触发上，这似乎不大可能（见Velasco et al，2008）。在给定周期，勒夫波具有更长的波长，并且这可能与对6.25级以上地震活动图像的影响有关。

6 结论

相比于随后的全球地震活动而言，2011年4月11日发生的M8.6地震是一次独特的地震事件，其特征是M≥6.5的地震活动经过简短的加速期后有一很长的平静期。它的独特之处通过将2012年主震后M≥6.5地震的间隔时间与过去一个世纪发生的所有大主震后的地震间隔时间进行比较，以及对过去10年发生的所有M≥8.5主震之后的震级—频度统计进行比较得到了证实。我们相信早期的加速和随后的平静是相关的，并是主震动态应力作用的结果。使用全球断层系应力作用一维模型简单破裂的判据，我们发现：（1）接近破裂的片区有一小部分产生了破裂，并导致了短期地震活动率增加；（2）在随后95天可能已产生破裂的多数其他片区使得短期无法维持M≥6.5地震的破裂。第一个发现是接近破裂的片区瞬时应力短期高于它们破裂阈值的结果。第二个发现是令人吃惊的，如果属实，将意味着来自遥远距离地震的瞬时动态应力可以改变断层的状态，比如暂时抑制大的破裂。

这导致了对之前概念的质疑，即动态应力仅能增加地震发生率，而不能抑制地震发生率。这也一直被用作区分动态应力机制和静态应力改变的基础（见Gomberg et al，1998；Felzer and Brodsky，2005；Toda et al，2012）。我们对一次M8.6主震的研究结果表明，动态应力导致了短期内全球地震活动率的增加（即动态应力要足够高），因而与该假设一致。动态应力阴影可在更长时间尺度上发展的观点已由我们的研究结果说明，但还需要通过更大区域范围的进一步研究来证实。这可以用最大（M≥8）地震的中间距离通过重复Parsons和Velasco等（2011）的分析来完成。也可以通过再访问明显短期增加可用动态应力解释的例子来完成（见 Kilb et al，2000；Gomberg et al，2003；Brodsky and Prejean，2005；Hill and Prejean，2007）。

数据与来源

地震震源和震级由美国国家地震信息中心（NEIC）地震目录、国际地震中心全球地震模型（ISC－GEM）目录和全球矩心矩张量（CMT）目录提供。全球矩心矩张量项目数据库是在www.globalcmt.org／CMTsearch.html上搜索到的（最后访问时间2013年7月）。国际地震中心全球地震模型（ISC－GEM）目录是全球地震模型工作的一 部 分， 见 http：／／www.globalquake－model.org（最后访问时间2013年4月）。

Bird，P.，Y.Kagan，and D.Jackson（2002）.Plate tectonics and earthquake potential of spreading ridges and oceanic transform faults，in，Plate Boundary Zones，S.Stein and J.Freymueller（Editors），Vol.30.American Geophysical U－nion，Washington，D.C.，203－218.

Bondár，I.，and D.Storchak（2011）.Improved location procedures at the international seismological centre，Geophys.J.Int.186，1220－1244.

Brodsky，E.E.，and S.G.Prejean（2005）.New con－straints on mechanisms of remotely triggered seismicity at Long Valley Caldera，J.Geophys.Res.110，no.B04302，doi：10.1029／2004JB 003211.

Brodsky，E.E.，E.Roeloffs，D.Woodcock，I.Gall，and M.Manga（2003）.A mechanism for sustained groundwater pressure changes induced by distant earthquakes，J.Geophys.Res.108，2390，doi：10.1029／2002JB002321.

Caine，J.S.，J.P.Evans，and C.B.Forster（1996）.Fault zone architecture and permeability structure，Geology24，1025－1028.

Dziewonski，A.M.，T.－A.Chou，and J.H.Woodhouse（1981）.Determination of earthquake source parameters from waveform data for studies of global and regional seismicity，J.Geophys.Res.86，2825－2852.

Ekström，G.，M.Nettles，and A.M.Dziewonski（2012）.The global CMT project 2004－2010：Centroid－moment tensors for 13，017earthquakes，Phys.Earth Planet.Int.200／201，1－9，doi：10.1016／j.pepi.2012.04.002.

Engdahl，E.E.，and A.Villaseñor（2002）.Global seismicity：1900－1999，in International Handbook of Earthquake and Engineering Seismology，W.H.K.Lee（Editor），Academic，Amsterdam，doi：10.1016／S0074－6142（02）80244－3.

Felzer，K.R.，and E.E.Brodsky（2005）.Testing the stress shadow hypothesis，J.Geophys.Res.110，doi：10.1029／2004JB003277.

Gomberg，J.，M.L.Blanpied，and N.M.Beeler（1998）.Earthquake triggering by transient and static deformation，J.Geophys.Res.103，24，411－24，426.

Gomberg，J.，P.Bodin，and P.A.Reasenberg（2003）.Observing earthquakes triggered in the near field by dynamic deformations，Bull.Seismol.Soc.Am.93，118－138.

Gonzales－Huizar，H.，A.A.Velasco，Z.Peng，and R.R.Castro（2012）.Remote triggered seismicity caused by the 2011 M9.0Tohoku－Oki，Japan earthquake，Geophys.Res.Lett.39，L10302，doi：10.1029／2012GL051015.

Goslin，J.，J.Perrot，J.－Y.Royer，and C.Martin（2012）.Spatiotemporal distribution of the seismicity along the Mid－Atlantic Ridge north of the Azores from hydroacoustic data：Insights into seismogenic processes in a ridge－hot spot context，Geochem.Geophys.Geosyst.13，Q02010，doi：10.1029／2011GC003828.

Hill，D.P.（2010）.Surface－wave potential for triggering tectonic（nonvolcanic）tremor，Bull.Seismol.Soc.Am.100，1859－1878.

Hill，D.P.，and S.Prejean（2007）.Dynamic triggering，in Treatise on Geophysics，G.Schubert（Editor），Vol.4，Earthquake Seismology.Elsevier，Amsterdam，258－288.

Kanamori，H.（1983）.Magnitude scale and quantification of earthquakes，Tectonophysics 93，185－199.

Kilb，D.，J.Gomberg，and P.Bodin（2000）.Triggering of earthquake aftershocks by dynamic stresses，Nature 408，570－574.

Manga，M.，I.Beresnev，E.E.Brodsky，J.E.Elkhury，D.Elsworth，S.E.Ingebritsen，D.C.Mays，and C.－Y.Wang（2012）.Changes in permeability caused by transient stresses：Field observations，experiments，and mechanisms，Rev.Geophys.50，doi：10.1029／2011RG000382.

McGuire，J.，and G.Beroza（2012）.A rogue earthquake off Sumatra，Sci.Express 336，doi：10.1126／science.1223－983.

Meng，L.，J.－P.Ampuero，J.Stock，Z.Duputel，Y.Luo，and V.C.Tsai（2012）.Earthquake in a maze：Compressional rupture branching during the 2012 MW8.6Sumatra earthquake，Science 337，724－726，doi：10.1126／science.1224030.

Parsons，T.（2005）.A hypothesis for delayed dynamic earthquake triggering，Geophys.Res.Lett.32，L04302，doi：10.1029／2004GL021811.

Parsons，T.，and A.A.Velasco（2011）.Absence of remotely triggered large earthquakes beyond the mainshock region，Nature Geosci.4，312－316.

Peng，Z.，and J.Gomberg（2010）.An integrated perspective of the continuum between earthquakes and slow－slip phenomena，Nature Geosci.3，599－607.

Pollitz，F.，R.S.Stein，V.Sevilgen，and R.Bürgmann（2012）.The 11April 2012east Indian Ocean earthquake triggered large aftershocks worldwide，Nature 490，250－253.

Prejean，K.，D.P.Hill，E.E.Brodsky，S.E.Hough，M.J.S.Johnston，S.D.Malone，D.H.Oppenheimer，A.M.Pitt，and K.B.Richards－Dinger（2004）.Remotely triggered seismicity on the United States west coast following the MW7.9 Denali fault earthquake，Bull.Seismol.Soc.Am.94，S348－S359.

Sevilgen，V.，R.Stein，and F.Pollitz（2012）.Stress imparted by the great 2004Sumatra earthquake shut down transforms and activated rifts up to 400km away in the Andaman Sea，Proc.Natl.Acad.Sci.Unit.States Am.109，doi：10.1073／pnas.1208799109.

Shearer，P.，and P.Stark（2011）.Global risk of big earthquakes has not recently increased，Proc.Natl.Acad.Sci.Unit.States Am.109，717－721.

Shelly，D.R.，Z.Peng，D.P.Hill，and C.Aiken（2011）.Triggered creep as a possible mechanism for delayed dynamic triggering of tremor and earthquakes，Nature Geosci.4，384－388.

Storchak，D.A.，D.Di Giacomo，I.Bondár，and J.Harris（2012）.The ISCGEM Global Instrumental Reference Earthquake Catalogue （1900－2009），AGU Fall Meeting，San Francisco，California.

Tape，C.，M.West，V.Silwal，and N.Ruppert（2013）.Earthquake nucleation and triggering on an optimally oriented fault，Earth Planet.Sci.Lett.363，231－241.

Toda，S.，R.S.Stein，G.C.Beroza，and D.Marsan（2012）.Aftershocks halted by static stress shadows，Nature Geosci.5，410－413，doi：10.1038／ngeo1465.

van der Elst，N.，and E.Brodsky（2010）.Connecting near－field and far－field earthquake triggering to dynamic strain，J.Geophys.Res.115，doi：10.1029／2009JB006681.

Velasco，A.A.，S.Hernandez，T.Parsons，and K.Pankow（2008）.Global ubiquity of dynamic earthquake triggering，Nature Geosci.1，375－379.

von Huene，R.，and D.W.Scholl（2012）.Observations at convergent margins concerning sediment subduction，subduction erosion，and the growth of continental crust，Rev.Geophys.29，279－316.

Wells，D.L.，and K.J.Coppersmith（1994）.New empirical relationships among magnitude，rupture length，rupture width，rupture area，and surface displacement，Bull.Seismol.Soc.Am.84，974－1002.

Yue，H.，T.Lay，and K.D.Koper（2012）.En echelon and orthogonal fault ruptures of the 11April 2012great interplate earthquake，Nature 490，245－249.

附录 全球地震活动性统计模型

概念模型

Pollitz等（2012）提出由印度洋地震产生的全球传播的地震波使足够数量接近破裂的片区承受了压力，致使其中许多在主震后几天内的一些M≥5.5地震中产生了破裂。他们将全球地震响应比作结满苹果的树木的晃动，其中一些已经成熟，并不可避免地由地震波震落下来。尽管这个想法是由2012年4月11日之前10天内地震活动率非常低而产生的，但对于多少潜在的片区会由于短暂的应力扰动，即传播的地震波而开始接近破裂，这可以用作有用的概念模型。我们设想潜在的起始位置处于应力张弛（可能在它们最后显著破裂之后）和应力增加到临界之间的随机分布状态。而且这些位置以恒定速率（假设为恒定的背景构造应力）成熟。这些简单假设的结果是，如果接近破裂位置的储集层在短时间内（即动态应力扰动后不久）因许多位置开始破裂而受扰动，那么在随后的时段可发生破裂的位置就会更少。

为了量化这个模型，我们假设对于任一M≥6.5地震，全球分布有N个可能破裂的片区。这些片区上我们假设平均应变积累率为˙ε，应变释放为Δε，平均破裂组合速率为λ。令片区应变为 ｛εi，i＝1，…，N｝。根据组合破裂速率，这些应变呈随机分布，因此在时间间隔ΔT内，片区群中发生破裂的概率为：

式中，εcrit（对所有i都＞εi）代表临界应变阈值，当应变积累到这个值时，给定片区上就会发生破裂。公式（A1）表示在断层群上地震发生的泊松模型中，在间隔时间ΔT内没有地震事件发生的概率为e－λΔT，其中1／λ为平均间隔时间。假设 ｛εi｝为均值分布，那么对于一个片区，则有：

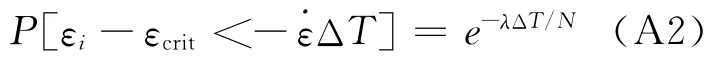
短期 触发

我们假设2012年4月地震的瞬时应变导致在破裂εd中所有片区的一部分f1均发生短期破裂；这些可相当于在震后最初10天内实际发生4个M≥6.5地震（图1d，3b）。根据全球传送的瞬时应变幅值的大小（Pollitz et al，2012），我们选择εd＝0.1μ应变。定义L为2012年4月地震发生时预期在破裂的εd内产生M≥6.5地震的片区数，因此短期内破裂的片区数为Lf1。如果应变状态在εcrit－Δε和εcrit之间随机分布，则有：

公式（A3）与经验结果一致，即远场触发的地震数往往与动态峰值应变的幅值呈线性关系（van der Elst and Brodsky，2010）。由于片区破裂时会经历应变降Δε，所以公式（A2）的左边为exp（－˙εΔT／Δε）。将它与公式（A2）右边等同，则有：

该式与公式（A3）组合则有：

更长 期平静

全球系统产生了Lf1的短期触发地震。这些地震本身不足以解释印度洋地震之后105天内预期M≥6.5地震的预算。正如主震后的平静一节中所述，图6意味着在震后10～105天内预期地震数与实际发生的4个之间有5.4个地震的明显空缺。如果这个算法正确，那么静止期的长度大致是预期的短期（触发）M≥6.5地震的2倍。然而，如果将这4个地震事件认为是独立现象，也就是说动态触发地震不是预期M≥6.5地震预算的部分，那么预计发生在震后105天内的M≥6.5地震数空缺会更大——图6所示8.4个地震。

由于我们处理的是小数统计，因此任何观察到的空缺都可能是随机的，尽管罕见，但统计偏差没有任何物理基础。另一种方式是在2012年4月主震之后，剩下的L×（1－f1）接近破裂片区中的一部分f2对破裂没有作用，尽管它们的应变状态与主震的动态应力相关。我们可将无M≥6.5地震发生的间隔时间Tquiet＝95天解释为复位系统产生一个地震事件所需要的概率为1－exp（－1）的时间。具体来说就是：

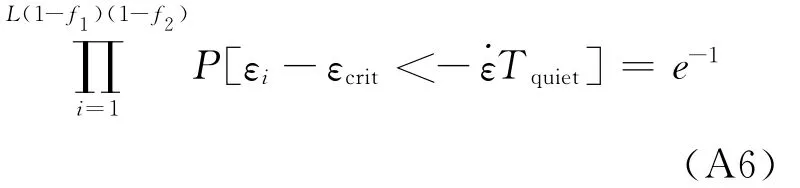
注意，公式（A6）考虑到了初始短期活动期间的Lf1地震事件。假设这些合格的L（1－f1）（1－f2）接近破裂的片区呈等同分布，那么对于一个片区我们有：

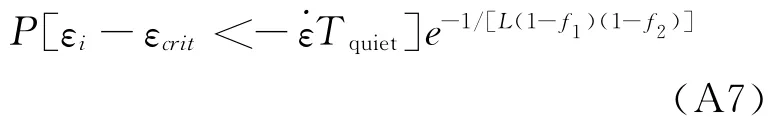
如果这些εi在 （εcrit－εd，εcrit）之间均匀分布，则公式（A7）的左边为exp［－˙εTquiet／εd］。将其与公式（A7）的右边等同，可得：

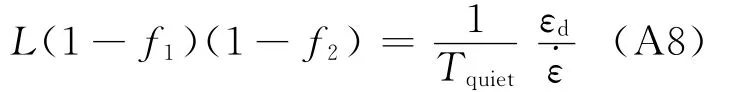
将公式（A5）中L的表达式代入公式（A8）中可得：

用约束条件Lf1＝4（短期触发地震的数，如图1d和3b所示）将公式（A5）和（A9）组合，我们就可求解L，f1和f2。通过使用参数˙ε＝0.05μ应变／年和εd＝0.1μ应变，可得到L＝66，f1＝0.061，f2＝0.88。对L的估计是合理的，因为它代表了在0.1μ破裂应变内荷载速率为0.05μ应变／年的片区数，即在两年时间间隔内成熟起始场地的数。假定发生率λ＝0.089／天，我们预计平均两年时间跨度内会发生66个M≥6.5地震。

讨论

M≥6.5地震震源片区的总数N通过合适选择Δε由公式（A4）给出。3MPa的典型应力降对应于Δε＝50μ应变，并且导致N＝32 800的全部震源片区。对应于M＝6.5地震的断层面积为164km2（Wells and Coppersmith，1994），因此我们理想的最小面积为5.4×106km2（最小，因为M≥6.5地震的断层面积更大）。这可与沿全球俯冲带和转换断层的孕震部分的总面积相比。全球俯冲带43 500km的总长度（von Huene and Scholl，2012）乘150km的下倾距离得到6.5×106km2。44 433km的转换断层总长度乘3km的平均耦合岩石层厚度（Bird et al，2002）得到面积为0.1×106km2，总面积为6.6×106km2。由我们简单的统计模型计算出的断层面积与受到高瞬态应变的活动断层的面积近似。

公式（A9）说明，当乘积λTquiet变大时，抑制片区中的部分f2也会变大。后者仅仅是图6中所示的8.4个地震空缺。该公式还说明，（1－f2）与（1－f1）成反比，因此如果现有成熟起始片区的较大部分在短期内破裂了，则f1将更大，而f2将相应地变小。因为推断的f1小，所以在短期内发生的4个地震事件仅仅是接近破裂的起始场地的一小部分。换句话说，这4个地震事件的发生从接近破裂场地的组合中去除了微不足道数量的场地。

如果接近破裂的场地的数L小于由公式（A5）规定的数，则抑制破裂的比例将变小，比如在2012年4月11日地震之前长时间段内M≥6.5地震发生率非常高的情况就如此。然而，主震前的发生率看来与30年的背景地震活动水平（图6）没有不同。如果认为2012年4月11日地震发生时短期触发的地震代表最接近破裂的片区，则抑制破裂的比例也会变小，也就是说，接近破裂的片区不会使2012年4月11日地震发生。在这种情况下，我们的分析仍然需要抑制其中f2＝1－1（5.4个地震）＝81%的破裂，这正好与图6中5.4个地震空缺一致。我们的结论是，不管其有效大小，2012年4月11日主震之后105天累计的5到9个地震空缺不是统计不确定性，就是需要通过抑制在这期间预期成熟的起始场地的破裂来考虑。