伊朗中东部地区的地震动衰减关系

Hosseyn Hamzehloo Majid Mahood

0 引言

涉及地震危险性分析评估的研究需要强地震动的预测。众所周知，地震危险性分析中的一些较大的不确定性由地震动衰减的不确定性造成。强地震动参数通常由（1）基于观测地震动峰值加速度（PGA）或反应谱（PSA）的经验衰减关系、（2）理论衰减关系和（3）模拟方法估算。

由于所使用的数据库不同，发表的地震动峰值加速度和反应谱的不同经验衰减关系给出的结果差异很大。此外，在一个包含不同地质、构造、地震学特征的区域使用单一的衰减关系可能会导致所得结果与实际值差异很大（Gupta et al，1997）。

近年来，大量学者基于随机模型建立了衰减关系（例如，Atkinson，1984；Boore and Atkinson，1987；Toro and McGuire，1987；Atkinson and Boore，1990，1995；Tavakoli and Pezeshk，2005）。这个模型起源于Hanks和 McGuire（1981）的工作，他们指出，观测到的高频地震动可以表征为有限持时、有限带宽的高斯噪声，具有震源和传播过程简单地震学模型规定的基本振幅谱（Atkinson and Boore，1995）。

最近，太平洋地震工程研究中心下一代地震动衰减项目（简称为PEER NGA项目）建立了一种新的衰减关系。根据Power等（2008）的文章，PEER NGA项目的目标是通过综合与高度互动的研究计划更新地震动经验模型。5个原已存在且被广泛使用的经验地震动模型的建立者参与了下一代衰减模型 的 建 立 （Boore and Atkinson，2008；Campbell and Bozorgnia，2008；Chiou and Youngs，2008；Idriss，2008）。PEER NGA项目的其中一部分是基岩地震动、土层场地效应和盆地效应的理论模拟，目的是为评价函数形式和确定地震动模型约束条件提供更科学的基础。

不同的研究者已经引入了基于地震学模型的理论衰减关系。Atkinson和Silva（2000）使用随机模拟方法建立了加利福尼亚地区的地震动衰减关系。该地震动衰减关系与加利福尼亚地区的经验强震数据库具有很好的一致性。在0.2～12Hz的频率上观测与模拟振幅平均比基本一致。由于使用了基于区域地震数据的衰减参数，该随机衰减关系与经验回归方程（例如，Abrahamson and Silva，1997；Boore et al，1997；Sadigh et al，1997）在震级—震中距范围，特别是大震中距时，吻合得很好。

强震动模拟可以为资料稀少的地区提供合成数据，用于建立衰减关系时补充或代替地震记录。不同的研究者已经使用模拟数据帮助建立了强地震动记录稀少的北美中东部地区的谱加速度衰减关系（Atkinson and Boore，1995；Toro et al，1997；Tavakoli and Pezeshk，2005）。

为克服波多黎各数据集的不完整性，Atkinson和 Motazedian（2003）使用了随机有限断层方法进行了地震动模拟。他们引入了动力学拐角频率的概念，并使用基于中等地震所得的参数作为模拟的输入参数，比较了该地区基于随机有限断层模型的地震动衰减关系与其他地区的地震动衰减关系。

伊朗中东部地区的地震活动具有震级高、复发周期长、分布散和沿几个第四纪断层存在地震空区的特点。该地区地震的震源通常很浅并与地表断层作用有关（Berberian，1976）。比如1978年的塔巴斯和2003年的巴姆破坏性地震就发生在这个地区。本文的目标是通过综合使用观测数据和基于地震学模型的模拟记录来建立伊朗中东部地区的地震动衰减关系。

1 岩石运动的随机有限断层模型

我们使用了Motazedian和Atkinson（2005）基于动力学拐角频率修正的随机有限断层模型。在该方法中，一条大断层被分成N个子断层。每个子断层被认为是一个小点源。按下式（Motazedian and Atkinson，2005）用适当的延时在时域内对子断层的地震动求和估计整个断层的加速度时程a（t）：

式中nl和nw分别是沿断层走向和下倾方向的子断层数目，Δtij是第ij个子断层辐射波到达观测点的相对时间延迟。根据Motazedian和Atkinson（2005）的文章，拐角频率是时间的函数（动力学拐角频率），破裂时程控制了每个子断层模拟时间序列的频率成分。下面是第ij个子断层的加速度谱Aij（f）（Motazedian and Atkinson，2005）：

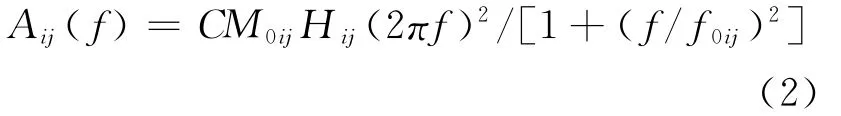
式中M0ij和f0ij是第ij个子断层的地震矩和动力学拐角频率Hij，由Motazedian和Atkinson（2005）给出如下：

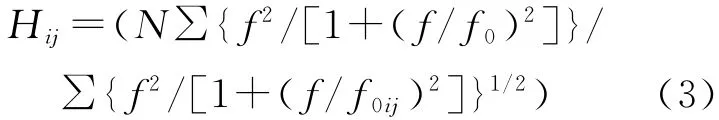
式中N是nl×nw。公式（2）中的常数C是：

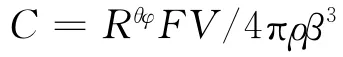
式中Rθφ是均值为0.55的辐射图案，F是等于2.0的自由表面放大系数，V是分配的两个水平分量（0.71），ρ是密度，β是剪切波速。我们分别在5.0～7.4震级范围和1～100km震中距范围生成了一大套伊朗中东部（ECI）地区的加速度时程。表1给出了使用随机有限断层模型合成所有模拟记录的输入参数。

表1 合成记录的建模参数

2 数据

本研究所用数据包括伊朗中东部地区的强地面运动观测记录和基于随机有限断层模拟方法的合成记录。其中，强地面观测记录由伊朗建筑与住宅研究中心（BHRC）观测和提供。

图1 1978年至2008年的地震（圆形）分布和伊朗建筑与住宅研究中心强震台站（三角形）的分布

图2 关于震级和震中距的观测数据分布

伊朗建筑和住宅研究中心观测数据集包括1978～2008年期间137个地震的497条记录。数据由SMA－1和SSA－2仪器记录。台站分布如图1所示。多数数据由SSA－2型仪器记录，阀值为10伽。我们从数据集中去除了震源参数、场地条件未知和信噪比低的数据。在5.0～7.4的震级范围内，观测数据最终被减少至106个地震的258条记录。基于Ghasemi等（2009）的研究，分析中考虑了硬岩石场地。在衰减模型中考虑了矩震级和Joyner－Boore震中距（Rjb）。观测记录的震级—震中距分布如图2所示。

我们使用随机有限断层模拟生成了一大套伊朗中东部地区5.0～7.5震级范围和1～100km震中距范围的加速度时程。这些模拟数据将弥补建立衰减关系时实测数据的不完整。

3 结果

我们对伊朗中东部地区考虑的衰减关系的表达式与Joyner与Boore（1993）给出的相同，如下所示：

式中Y是地震动峰值加速度或反应谱的水平分量平均值，以g（g＝981cm／s2）为单位；MW是矩震级；rjb是到断层破裂地表投影的最近距离，以km为单位；h是伊朗中东部地区平均震源深度；a，b，c和d是由回归分析确定的系数；第i个事件第k个记录的残差分别由εe和εr描述，n是每个事件的记录数（Joyner and Boore，1993）。模型中的这两个随机项εr和εe被认为符合零均值的正态分布。

回归分析是以Joyner和Boore（1993）的两步模型为基础。预测地震动的系数由非线性回归估计，也是基于Joyner和Boore（1993）的模型。

首先我们建立了基于109个地震258条强地面运动观测数据的衰减模型。这些地震的基本参数在本文的电子补充材料表S1（译文从略——译注）中给出。表2给出了回归系数。基于观测数据的衰减模型如图3所示。为估计5.0～7.4震级范围震中距直到100km的衰减关系，我们使用随机有限断层模型生成了一套该震级和震中距范围的加速度时程。

由图2可见，观测数据在震级5.6～

6.3区间、震中距100km范围内存在空区。此外，震级6.3～7.4区间、震中距70km范围内也存在空区。对于震中距＜10km，5.0～7.4的震级范围空区显得尤其明显。

表2 基于观测数据的衰减关系的系数1）

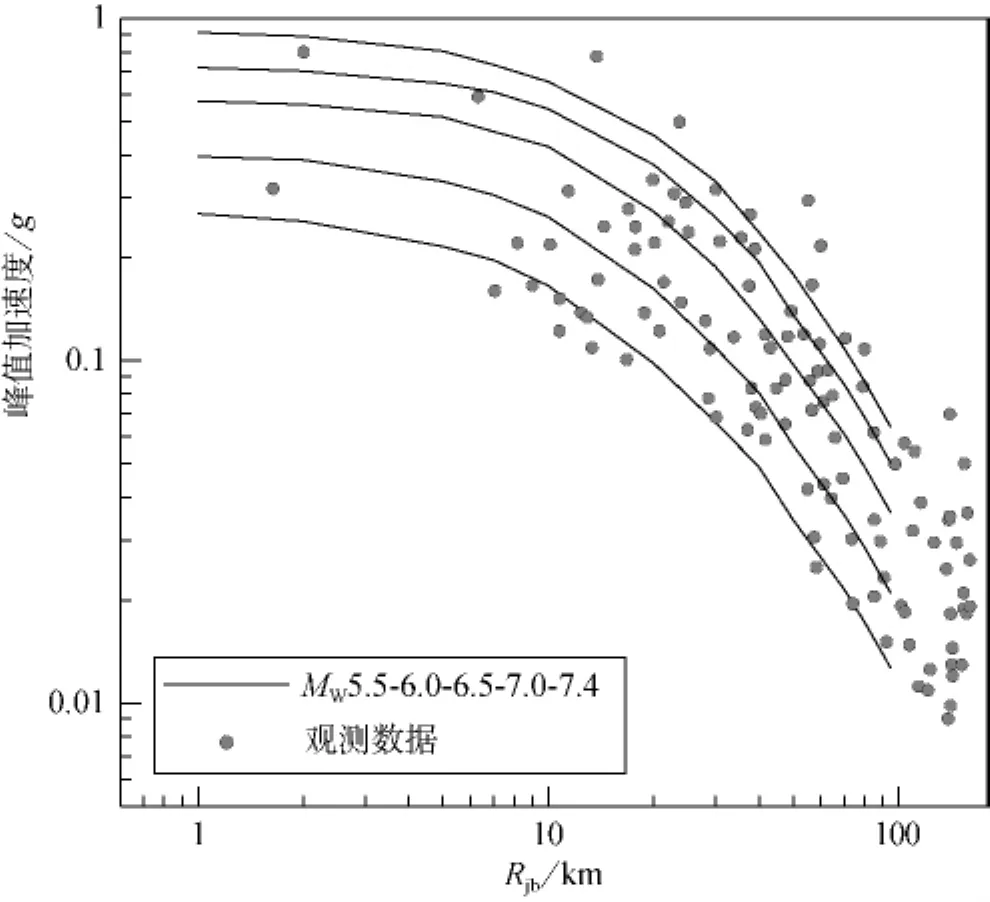
图3 中值衰减关系与观测数据的对比

根据表1中给出的模型参数，我们首先模拟了2003年巴姆地震。这对于验证用于生成该地区一套震级—震中距的加速度时程记录的地震学参数很重要。图4和图5给出了观测的和模拟的加速度时程与傅里叶振幅谱。Sarkar（2005）和 Mahood与 Hamzehloo（2009）根据伊朗中东部地区的记录数据分析获得了这些地震学参数。这些参数用于伊朗中东部地区的加速度时程模拟。

根据观测和模拟数据估计了衰减关系的系数，列于表3。

图6给出了基岩场地地震动峰值加速度与反应谱衰减关系曲线，其中反应谱的周期分别为0.2，0.3，0.5，1.0和2.0s。

图4 巴姆台观测的和模拟的加速度时程

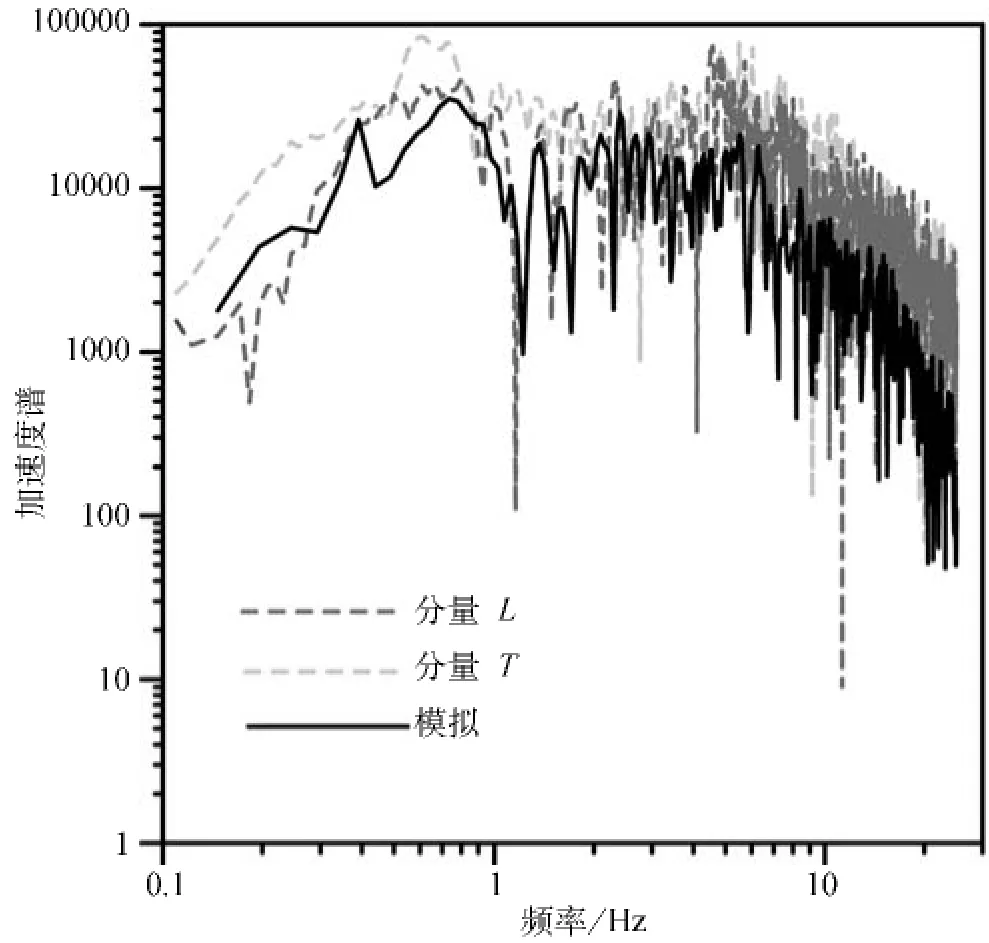
图5 巴姆台观测的和模拟的傅氏振幅谱

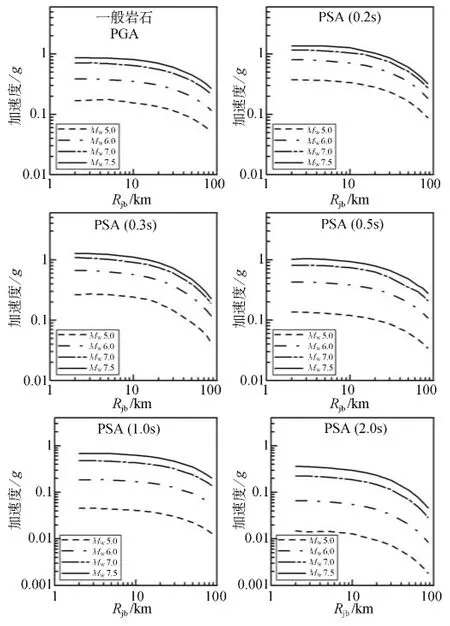
图6 岩石场地的地震动峰值加速度（PGA）和反应谱（PSA）地震动衰减关系

4 讨论

把未来地震的地震动估计为震级和震中距的函数是地震工程的一个重要问题。表3列出的衰减关系被认为适用于估计伊朗中东部地区基岩场地条件下5.0～7.4震级范围的地震动。用于建立衰减关系的数据主要是观测和模拟记录。模拟记录基于伊朗中东部地区的地震学参数合成。因为伊朗中东部地区强地面运动观测资料太缺乏，不能由观测数据直接建立地震动衰减关系，所以合成了该地区地震动记录。

残差标准差表达了地震动的随机变化性，它是地震危险性分析的重要参数。仅使用观测数据，残差标准差变化范围为0.37～0.41（表2）。同时采用了观测数据和模拟数据，残差标准差的变化范围减少为0.29～0.37（表3）。观测数据的标准差较大是由于观测数据不完整，特别是在震中距＜10km时（图2）。

图7显示了回归残差分别随矩震级和震中距Rjb的变化。对全部震中距和震级范围，在所有频率上，观测数据的残差在－2～＋2的范围变化，而模拟数据的残差变化范围是－1～＋1（图7）。

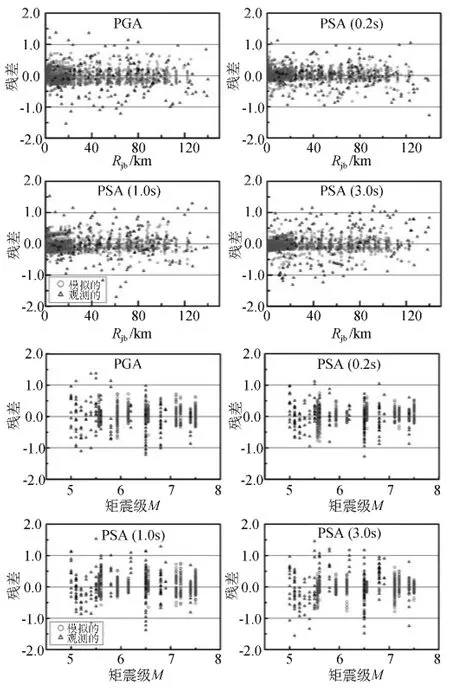
图7 由观测（三角形）和模拟（圆形）数据推导衰减模型预测的地震动峰值加速度（PGA）和加速度反应谱（PSA）对矩震级和Rjb的回归残差的比较

图8 绘出了衰减模型的残差直方图。地震动峰值加速度和加速度反应谱的每组残差由正态分布拟合，这呈现了预期的基于计算标准差的正态概率分布函数。可以观察到，对于方程（4）提出的模型预期和估计的概率分布函数匹配得很好。

图9给出了塔巴斯地区两个地震（1978年9月16日MW7.4地震和1998年3月14日MW6.9地震）记录的频谱值。

我们将获得的伊朗中东部地区衰减关系和最近发表的衰减关系进行了对比。图10给出了震中距为10km时，选取的地震动衰减关系和我们的地震动衰减关系预测的加速度反应谱中值的对比结果。

为了验证本研究建立的地震动衰减关系，在图11中我们把对MW7.0事件的地震动峰值加速度估计值和周期为0.2，1.0和2.0s的加速度估计值与世界范围的地震动衰减关系的相应估计值做了对比。结果表明，我们的预测加速度反应谱和最近的衰减模型的估计值具有可比性。

表3 由PGA和PSA回归分析得到的系数和统计参数1）

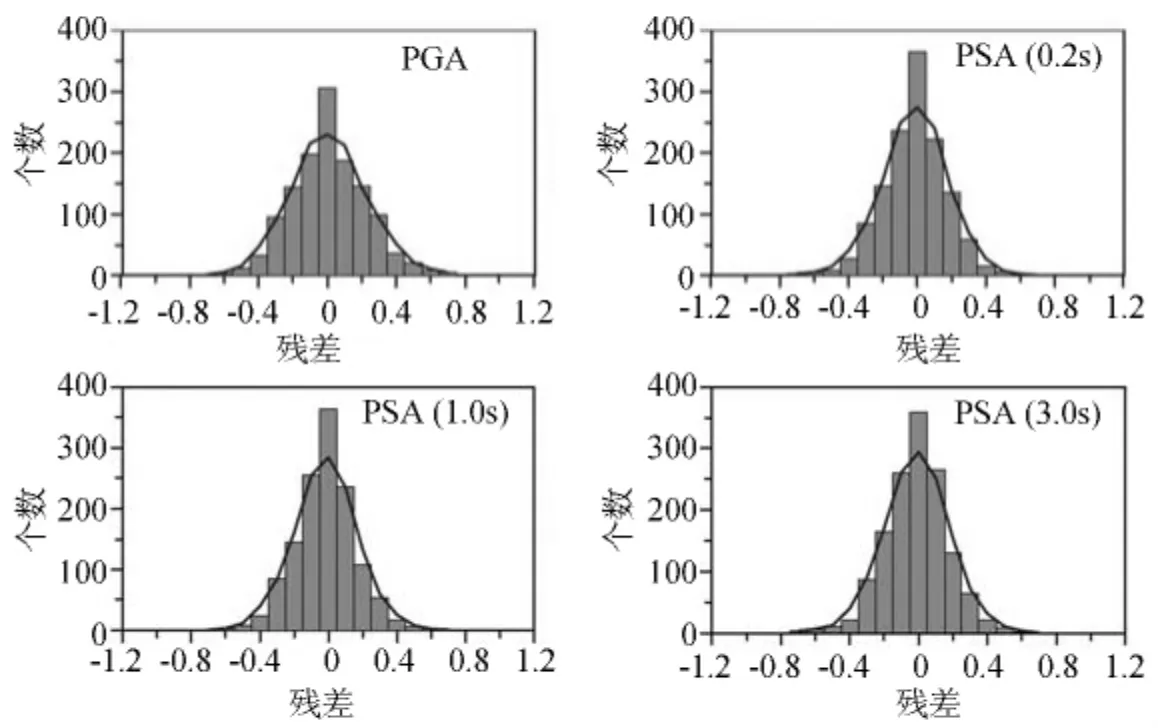
图8 所提出模型的残差直方图

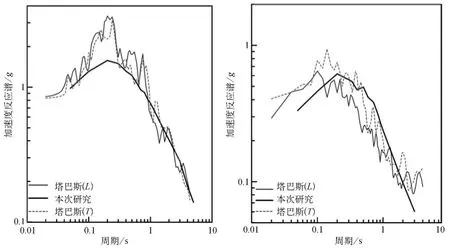
图9 1978年9月16日塔巴斯MW7.4地震（左）和1998年3月14日MW6.9地震（右）两个记录的频谱值

图10 由8个地震学和工程一般岩土场地条件广泛使用的经验地震动关系预测的5%阻尼加速度反应谱的比较。用于比较的震级是MW7.0，震中距是10km

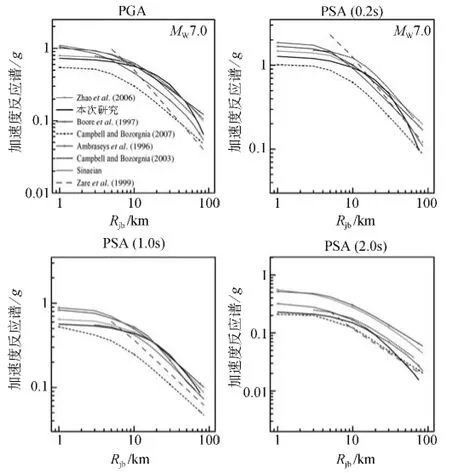
图11 几个被广泛应用的硬岩石场地条件衰减关系与本研究建立的混合经验地震动衰减关系计算的MW7.5地震动峰值加速度和5%阻尼在周期点0.2，1.0和2.0s上加速度反应谱的比较

5 结论

我们认为提出的衰减关系适用于估计伊朗中东部地区基岩场地条件的地震动加速度峰值水平分量和阻尼为5%的反应谱。本研究首次联合使用观测记录和基于随机有限断层法的模拟记录，建立了伊朗中东部地区的理论—经验衰减关系。本研究所得水平向地震动峰值加速度和反应谱理论—经验衰减关系适用于震中距100km以内、震级MW5.0～7.4间的地震动估计。

数据与来源

地震动记录由伊朗建筑与住宅研究中心提供（http：／／www.bhrc.ac.ir／portal／，最后访问时间2011年5月）。一些仪器的位置和震级（电子补充材料的表 S1）取自国际地震中心 （http：／／www.isc.ac.uk／ehbbulletin／search／catalogue／， 最后访问时间2012年6月）。

Abrahamson，N.，and W.Silva（1997）.Empirical response spectral attenuation relations for shallow crustal earthquakes，Seismol.Res.Lett.68，94－127.

Abrahamson，N.A.，and W.J.Silva（2008）.Summary of the Abrahamson ＆Silva NGA ground motion relations，Earthquake Spectra 24，no.1，67－97.

Ambraseys，N.N.，A.Simpson，and J.J.Bommer（1996）.Prediction of horizontal response spectra in Europe，Earthquake Eng.Struct.Dynam.25，371－400.

Atkinson，G.（1984）.Attenuation of strong ground motion in Canada from a random vibrations approach，Bull.Seismol.Soc.Am.74，2629－2653.

Atkinson，G.，and D.Boore（1990）.Recent trends in ground motion and spectral response relations for North America，Earthquake Spectra 6，15－36.

Atkinson，G.，and D.Boore（1995）.New ground motion relations for eastern North America，Bull.Seismol.Soc.Am.85，17－30.

Atkinson，G.，and D.Motazedian（2003）.Earthquake magnitude measurements for Puerto Rico，USGS Award No.02HQGR0054.

Atkinson，G.，andW.Silva（2000）.Stochastic modeling of California ground motions，Bull.Seismol.Soc.Am.90，255－274.

Berberian，M.（1976）.Contribution to the seismotectonics of Iran（Part II），Geological Survey of Iran，Rept.No.39，141pp.

Boore，D.M.，and G.M.Atkinson（1987）.Stochastic prediction of ground motion and spectral response parameters at hard－rock sites in eastern North America，Bull.Seismol.Soc.Am.77，440－467.

Boore，D.M.，and G.M.Atkinson（2008）.Groundmotion prediction equations for the average horizontal component of PGA，PGV，and 5%－damped PSA at spectral periods between 0.01s and 10.0s，Earthquake Spectra 24，99－138.

Boore，D.，W.Joyner，and T.Fumal（1997）.Equations for estimating horizontal response spectra and peak acceleration from western North American earthquakes：A summary of recent work，Seismol.Res.Lett.68，128－153.

Campbell，K.W.，and Y.Bozorgnia（2003）.Updated near－source groundmotion（attenuation）relations for the horizontal and vertical components of peak ground acceleration and acceleration response spectra，Bull.Seismol.Soc.Am.93，no.1，314－331.

Campbell，K.W.，and Y.Bozorgnia（2007）.NGA Ground Motion Relations for the Geometric Mean Horizontal Component of Peak and Spectral Ground Motion Parameters，Pacific Earthquake Engineering Research Center，University of California，Berkeley，PEER 2007／2.

Campbell，K.W.，and Y.Bozorgnia（2008）.NGA ground motion model for the geometric mean horizontal component of PGA，PGV，PGD and 5%damped linear elastic response spectra for periods ranging from 0.01to 10s，Earthquake Spectra 24，139－171.

Chiou，B.S.J.，and R.R.Youngs（2008）.Chiou－Youngs NGA ground motion relations for the geometric mean horizontal component of peak and spectral ground motion parameters，Earthquake Spectra 24，173－215.

Ghasemi，H.，M.Zare，Y.Fukushima，and K.Koketsu（2009）.An empirical spectral ground－motion model for Iran，J.Seismol.13，no.4，499－515，doi：10.1007／s10950－008－9143－x.

Gupta，I.D.，V.Rambabu，and B.M.Rame Gowda（1997）.An integrated PGA attenuation relationship，Bull.ISET，Paper No.368，34，no.3，137－158.

Hanks，T.C.，and R.K.McGuire（1981）.The character of high frequency strong ground motion，Bull.Seismol.Soc.Am.，71，no.6，2071－2095.

Idriss，I.M.（2008）.An NGA empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes，Earthquake Spectra 24，217－242.

Joyner，W.B.，and D.M.Boore（1993）.Methods for regression analysis of strong－motion data，Bull.Seismol.Soc.Am.，83，no.2，469－487.

Mahood，M.，and H.Hamzehloo（2009）.Estimation of coda wave attenuation in East Central Iran，J.Seismol.13，125－139.

Mahood，M.，H.Hamzehloo，and G.J.Doloei（2009）.Attenuation of high frequency P and S waves in the crust of the East－Central Iran，Geophys.J.Int.179，1669－1678.

Motazedian，D.，and G.Atkinson（2005）.Stochastic finite fault modeling based on a dynamic corner frequency，Bull.Seismol.Soc.Am.95，no.3，995－1010.

Ohno，S.，K.Takahashi，and M.Motosaka（2001）.Empirical estimation of horizontal and vertical motions based on California earthquake records and its application to Japan inland earthquakes，J.Struct.Construct.Eng.（Trans.AIJ）544，39－46（in Japanese）.

Power，M.，B.Chiou，N.Abrahamson，Y.Bozorgnia，T.Shantz，and C.Roblee（2008）.An overview of the NGA Project，Earthquake Spectra 24，no.1，3－21.

Sadigh，K.C.，Y.Chang，J.A.Egan，F.Makdisi，and R.R.Youngs（1997）.Attenuation relationships for shallow crustal earthquakes based on California strong motion data，Seismol.Res.Lett.68，180－189.

Sarkar，I.，V.SriRam，H.Hamzehloo，and K.N.Khattri（2005）.Subevent analysis for the Tabas earthquake of September 16，1978，using near field accelerograms，Phys.Earth Planet.Int.151，53－76.

Tavakoli，B.，and S.Pezeshk（2005）.Empirical－stochastic ground－motion prediction for North America，Bull.Seismol.Soc.Am.95，no.6，2283－2296.

Toro，G.，and R.McGuire（1987）.An investigation into earthquake ground motion characteristics in eastern North America，Bull.Seismol.Soc.Am.77，468－489.

Toro，G.，N.Abrahamson，and J.Schneider（1997）.Model of strong ground motion in eastern and central North America：best estimates and uncertainties，Seismol.Res.Lett.68，41－57.

Zare，M.，M.Ghafory－Ashtiany，and P.Y.Bared（1999）.Attenuation law for the strong motions in Iran，in Proceedings of Third International Conference on Seismology and Earthquake Engineering，May 17－19，Tehran，I.R.Iran.

Zhao，J.X.，J.Zhang，A.Asano，Y.Ohno，T.Oouchi，T.Takahashi，H.Ogawa，K.Irikura，H.K.Thio，P.G.Somerville，Yasuhiro Fukushima，and Yoshimitsu Fukushima（2006）.Attenuation relations of strong ground motion in Japan using site classification based on predominant period，Bull.Seismol.Soc.Am.96，no.3，898－913.