北美地区地震烈度预测方程

Gail M.Atkinson C.Bruce Worden David J.Wald

0 引言

作为震级和距离函数的预测有感烈度和破坏效应的方程是评估地震危险与风险及解释当代与历史地震信息的有用工具。美国地质调查局执行的 “你感觉到了吗？”（DYFI）（Wald et al，1999）项目一直在收集追溯到过去几十年的庞大地震感觉效应数据库。民众使用互联网网站（见 “数据与来源”一节）通过回答简单的多选调查问卷报告他们的经历。通过应用一个简单算法（Wald et al，1999；Dewey et al，2000），这些问题成为对观测者所处位置修正的麦加利烈度（MMI；Wood and Neumann，1931；Dewey et al，1995）的特征量。MMI在从1（无感）到10（严重破坏）的定性标度上测量地震动烈度。虽然目前一般不给出大于10的MMI值，但它起初的标度最大值可达到12（完全破坏，Dewey et al，1995）。本文的其余部分标识I（而不是 MMI）的烈度值是根据像 “户内有感”（I＝3）到 “所有人有感，窗户、餐具、玻璃器皿破碎、薄涂层破裂”（I＝6）到 “一些结构完全毁坏”（I＝9）的描述来赋值的。注意，该标度起初使用罗马数字定义，它可与本文中相应的其他数字互换使用。DYFI项目平均邮政编码区域或其他地理编码区域内很多人的烈度响应，提供烈度的平均测量值及其跨越影响区域的变化。

自从1999年实施以来，DYFI项目发展迅速，响应者数目增长很快。图1汇编了到目前为止的美国响应，提供了过去15年全国地震活动和有感地震影响的令人感兴趣的快照。单个地震的烈度图一般是根据数百个邮政编码区域收集的成千上万个响应绘制的。在中等地震有感范围很大的美国东部（EUS）地区，通常有数以万计的响应。比如，2011年弗吉尼亚米纳勒尔5.8级地震导致了超过144 000人的响应。如Atkinson与Wald（2007）示出的一样，地震烈度与仪器地震动测量结果相关性好得惊人，因此可以说，丰富的烈度数据库是仅次于丰富的仪器地震动数据库的好数据库。对于2011年米纳勒尔地震，收集的大量烈度数据使得能够获得关于震源、衰减和场地过程的一些令人感兴趣的结论（例如，Hough，2012），不是所有这些结论都可以通过仪器数据得到。总之，烈度资料往往在数量上弥补了质量上的不足。

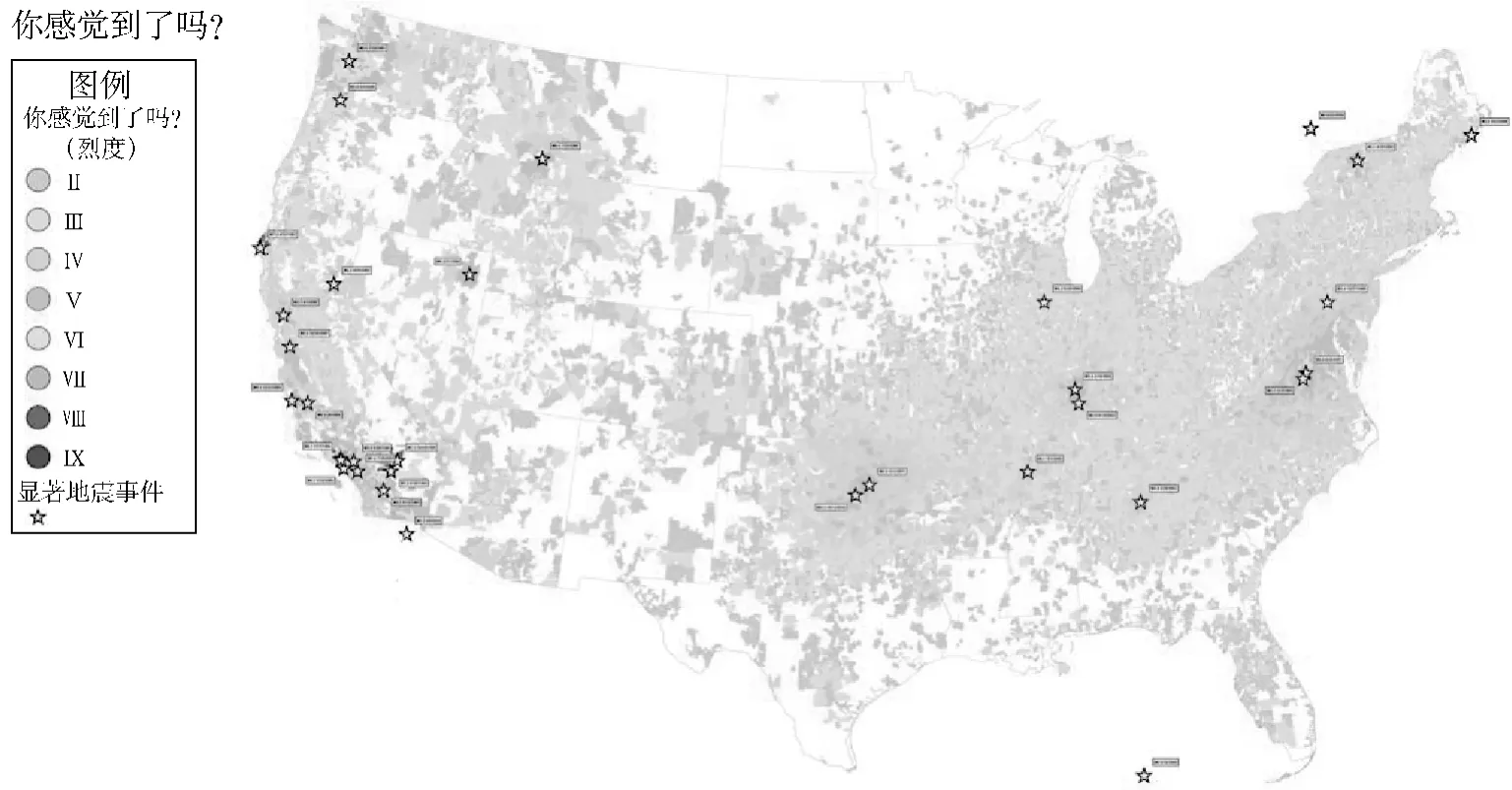
图1 “你感觉到了吗？”项目报告的1991～2013年美国连续地区累积最大报告烈度 （DYFI：或等效程序）。星号表示显著地震事件 （DYFI广泛报告的事件）

Atkinson与 Wald（2007）使用DYFI数据库（到2006年），结合稀少的历史烈度数据对北美东、西部地区（ENA，WNA）导出了作为矩震级（M）和到断层最短距离（Df）函数的平均地震烈度预测方程（IPE）。对每个地震事件，他们把由邮政编码和距离报告的平均烈度值分了段，这些数据被用于回归分析，在回归分析中，I是应变量，M 和Df是自变量。因为由邮政编码报告的烈度在很大区域上被空间平均，且通过距离分段实现进一步的空间平均，所以烈度预测方程隐含平均场地条件。

图2提供了分段烈度观测结果及得到它们的DYFI邮政编码数据的例子。在图2上没有画出少于3个响应者的邮政编码区域；仅当距离段含有4个或更多响应时才计算I的均值。本图画出了美国东部和加州约M5.5地震事件观测结果与Atkinson和Wald（2007；AW07）烈度预测方程的对比。直到预测烈度低于约2.5的距离（这个距离在加州约200km，在美国东部约600km），AW07烈度预测方程一般良好地表达了烈度。对于低烈度的远距离，存在一些众所周知的获取烈度值的困难。其中一个困难是人们更喜欢报告有感而不报告无感引起的报告偏差。更重要的是，烈度本质上在标度的低端是有界的，当我们靠近地震的震动感觉极限时，它导致了远距离的烈度偏差，这类似于强地面运动地震学中的触发偏差（例如，Joyner and Boore，1981）。因此，我们认为在地震事件被感觉的最远距离上，DYFI烈度不是可靠的平均烈度量度。

总的说来，AW07的烈度预测方程已经成功地描述了在DYFI项目下报告的地震动水平和烈度。比如，图3示出了2000年至2013年年中加州和美国东部具有1 000个以上响应的M＞3.5且其预测烈度Ipred≥2.5（为消除弱烈度偏差影响）的所有地震事件相对于AW07烈度预测方程的残差。以（Iobs－Ipred）作为残差，其中Iobs是基于逐个事件编辑的分段烈度数据（以0.2个对数距离段为单位），Ipred是对事件震级由AW07预测的I值（AW07的烈度预测方程使用Df作为预测变量，它在DYFI数据库中实际上被计算为地震事件的震源距，但如果对所有数据制表，可以对任何距离度量方式画出残差曲线；为了方便，这里使用了震中距）。基于这些接近于0的平均残差，不存在修正这些方程的统计依据（虽然美国东部的地震烈度被高估的可能性在残差中有所显现）。然而，AW07方程的一个问题是对大地震事件（M＞6）预测了近距离处的不切实际的中值烈度。比如，AW07烈度预测方程对加州M8地震在20km内、美国东部M7.5地震在35km内会预测I＞9的烈度，对东部M8地震预测的最大烈度会超过10。

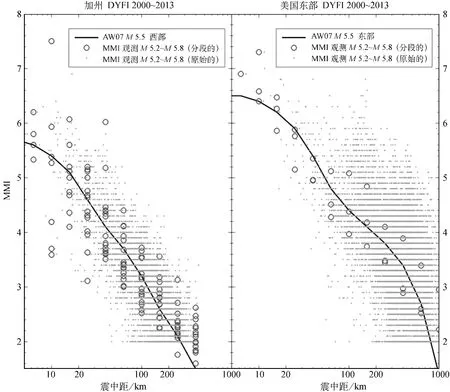
图2 2000～2003年M5.2～5.8地震分段烈度数据（圆圈）与Atkinson和 Wald（2007）对M5.5地震的烈度预测方程（曲线）的对比。圆点表示分段前各邮政编码区域的DYFI值。该图的彩色版仅适用于电子版本

AW07中近源的中值烈度偏高是由于缺少足够的高震级近距离烈度数据来约束烈度预测方程造成的。相比之下，像下一代衰减关系－西1（NGA－West 1）与下一代衰减关系－西2（NGA－West 2）计划（例如，Power et al，2008；Bozorgnia et al，2014，及其内的参考文献）这样的地震动预测方程（GMPE）在近距离具有相对较好的约束，蕴含着地震动幅值随震级和距离的显著饱和。尚不清楚地震烈度中的饱和效应是否在仪器观测数据中也有隐含反应。然而，假定仪器观测数据和感觉烈度相关良好（Atkinson and Wald，2007；Worden et al，2012），我们就可以合理地想到对大地震和近距离，其烈度曲线会有一定程度的收缩。

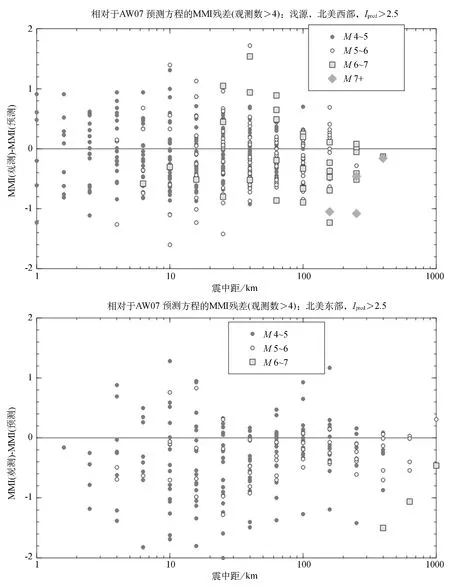
图3 2000～2013年加州（上图）和东部（下图）M≥4且Ipred≥2.5的地震事件的烈度残差

通过烈度预测方程与地震动预测方程之间 “闭合环路”，可以实现AW07预测方程的改进，进而更好地约束大震近距离的烈度标度。最近的统计研究（Worden et al，2012；下文中称W12）给出了标绘加州地震烈度I与地震动量度相互间的稳健相关；这些稳健相关被称为地震动烈度相关方程（GMICE）。在本项研究中，我们使用 W12的地震动烈度相关方程比较了地震动预测方程和烈度预测方程（使用Boore et al，2014，NGA－West 2地震动预测方程），先对加州地震进行了比较。最近的地震动预测方程在很宽的震级和距离范围上受到约束，使地震动预测方程预测的烈度I（通过W12地震动烈度相关方程）在宽的叠加数据范围上（M3.5～6.5，距离到100km）稳健地校准到DYFI观测数据上。根据烈度与地震动预测结果的这种协调，我们对加州地震提出了修正的烈度预测方程。基于加州地震的烈度预测方程对北美西部（WNA）的浅源地震事件（典型深度5～15km）一般应该是适用的，但对板内深源地震或西北太平洋俯冲地震事件未必适用。这一预期根据的是全球地震动预测方程证实的全球活动构造区中浅源地震事件地震动的相似性。在北美东部，由于滞弹衰减较小，我们预期烈度随距离的衰减比北美西部更慢；由于应力降较高，我们也预期较高的近源值。为了模拟这些趋势，我们用 “参考经验方法”（Atkinson，2008）推导了匹配美国东部烈度观测结果的北美西部烈度预测方程的校正因子。这个过程产生了相应的北美东部的烈度预测方程。我们对北美修正的烈度预测方程遵从非常类似于AW07的函数形式，但在大震级近距离的表现更符合实际。

1 北美西部烈度预测方程的修正

我们通过对由AW07预测的烈度与用Boore等（2014）地震动预测方程（对走滑地震）和Worden等（2012）地震动烈度相关方程预测的仪器烈度进行比较开始，来确定它们在由数据约束的震级距离范围内覆盖的程度。具体地说，Boore等（2014）预测了包括作为震级、距离和场地条件函数的地震动峰值加速度（PGA）、地震动峰值速度（PGV）和响应谱的水平分量地震动参数的与取向无关的均值。假定地壳上部30m内的平均剪切波速（VS30）为450m／s，相应于国家地震减灾计划C类（NEHRP C）场地放大率，我们使用Boore等（2014）的方法在震级距离空间上建立了预测的地震动峰值加速度和地震动峰值速度值的网格。我们判断国家地震减灾计划C代表了我们国家的平均场地条件，这个判断得到了Boore等（2014）数据库中VS30的均值也约为450m／s的观测结果的支持。而且，一些灵敏性检查揭示出，我们的结果总体上对平均场地条件的选择并不敏感。我们承认，场地条件差异很大，在后面我们将说明较软和较硬场地条件的影响。使用Atkinson与Adams（2013）给出的基于给定矩震级的平均长度垂直断层的简单几何校正，我们把Boore等（2014）中使用的Joyner－Boore距离标度转换成包括等效震中距和震源距的其他距离标度。

联合使用由Boore等（2014）给出的震级－距离空间中VS30＝450m／s的地震动峰值加速度和地震动峰值速度值网格和W12的方程（6），根据地震动峰值加速度和地震动峰值速度预测烈度 ［我们忽略了因W12使用最大水平分量而Boore等（2014）使用平均水平分量量度产生的微小差异，我们认为这种差异在本研究的背景下不重要］。我们把由地震动峰值加速度和地震动峰值速度预测值的平均值作为仪器烈度的最佳估计值。这样做是合理的，因为它提供了对烈度的带宽影响，这可能是Worden等（2012）发现同时使用地震动峰值加速度和地震动峰值速度略优于单独使用其中一个参数的原因。而且，除地震动峰值速度外还使用地震动峰值加速度解释了对同样的震级在东部通常观测到甚至是在近距离观测到的较高烈度的事实（Atkinson and Wald，2007）。我们推测，北美东部较高的地震烈度可能起因于北美东部地震动额外的高频成分，地震动峰值加速度比地震动峰值速度可在更大程度上捕获这种高频成分。注意，根据地震动峰值加速度或地震动峰值速度获得烈度的W12方程含有距离项。因为在很近或很远处的距离校正项不受数据的约束，我们在方程（6）的应用中使用了最小10km和最大300km来约束W12中的距离校正项。

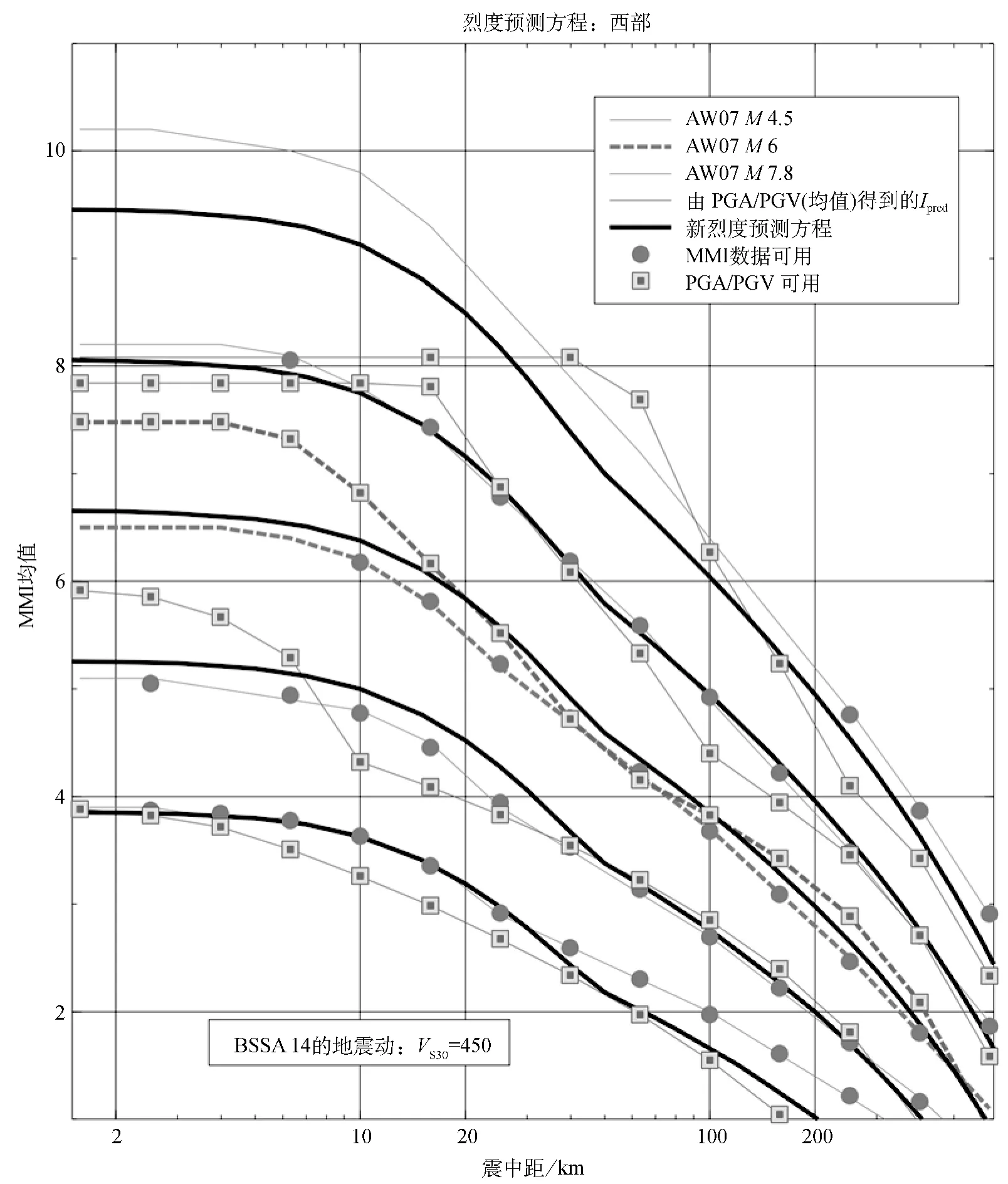
图4 对北美西部（WNA）M4，5，6，7，8地震事件使用峰值地震动加速度（PGA）和峰值地震动速度（PGV），由BSSA14地震动预测方程（GMPE）和 W12地震动烈度相关方程（GMICE）预测的烈度与AW07烈度预测方程（IPE）的对比。圆圈表示受修正麦加利烈度数据约束的AW07的震级—距离段，而方块表示受PGA和PGV约束的BSSA14的震级—距离段。粗黑线表示新IPE（由这两种估计值的均值回归得到）。该图的彩色版仅适应于电子版本

图4对加州事件比较了如上述基于由地震动峰值加速度或地震动峰值速度推断的均值烈度和由AW07根据DYFI数据直接预测的烈度；为了使比较清楚明了，我们把基于Boore等（2014）和基于AW07的估计值都转换成了随震中距的变化。用符号示出了由可应用基础方程 ［AW07和Boore等（2014）］中数据约束的震级—距离范围。通过以0.5震级单位分段和0.2个震中距（km）对数单位进行数据分段，评价了方程是否受到数据的约束；图4上画出的符号表明数据在参考方程中那个震级—距离段是可用的。我们观察到这些烈度预测结果在二者同被数据约束的震级—距离范围内非常一致。对震级很高的大震事件（M～8），在近距离上由于地震动预测方程中的强饱和影响，基于地震动预测方程的烈度估计值显著低于AW07的烈度估计值。对于M5和6地震事件，观察到了相反的趋势。对于M4和7地震事件，基于地震动预测方程与AW07的烈度预测方程估计值在整个感兴趣的距离范围上惊人地一致。

基于地震动预测方程和AW07的烈度具有良好的烈度一致性，我们建议修正的烈度预测方程应该以这两种烈度估计值的均值为基础。这将给出一个在烈度预测方程受到良好约束的震级—距离范围内与AW07非常相似的烈度预测方程，但它会更好地反映地震动数据中隐含的近源较低烈度。我们要指出的是，烈度会否达到与地震动相同的饱和程度尚不清楚。

为了对北美西部获得修正的烈度预测方程，我们在震级—距离空间内创建了一个基于地震动预测方程和AW07烈度（等权重）的平均烈度值的目标网格（使用AW07的震源距量度，这里对加州我们假设震源深度平均为8km，把震中距映射成震源距）。我们从M3.5到8以0.5个震级单位间隔和等对数间隔震中距（1.6，2.5，4.0，6.3，10，16，25，40，63，100，160，250，400和630）定义目标网格。我们发现，使用类似于Atkinson与 Wald（2007）所用的函数形式，

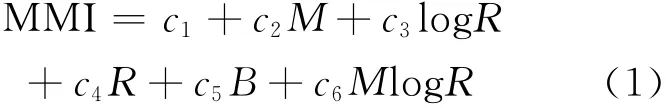
能够密切拟合这些目标值的网格（达到0.15个单位之内的平均绝对误差）。式中R＝

是震源距，B＝max（0，log（R／50））。表1列出了由烈度值目标网格回归得到的方程（1）的系数。图4画出了导出的方程。在我们的函数形式中，R是在震源近处加入近距离饱和的有效距离量度。通过附加项（＋14

2

）达到了饱和，虽然该附加项不严格等于震源深度，但它提供了典型震源深度地震事件的适当饱和。

方程（1）与 Atkinson和 Wald（2007）方程之间函数形式的重要差异是方程（1）中没有M2项，所以在固定的距离上震级值变化时震级标度不变化。换句话说，大震近距离曲线不收缩；仅有的震级依赖形状特征是，由于MlogR中该项的存在，不同震级衰减曲线之间烈度的差异随距离增加而变化。在最初的回归中，我们包含了M2项。然而，我们发现M2项在统计上不显著，把它去除后重复了回归。这意味着，不像地震动幅值那样，我们用方程拟合的目标烈度值不具有可分辨的近距离饱和效应；这可能反映了缺少饱和效应或求解它们的数据不足。

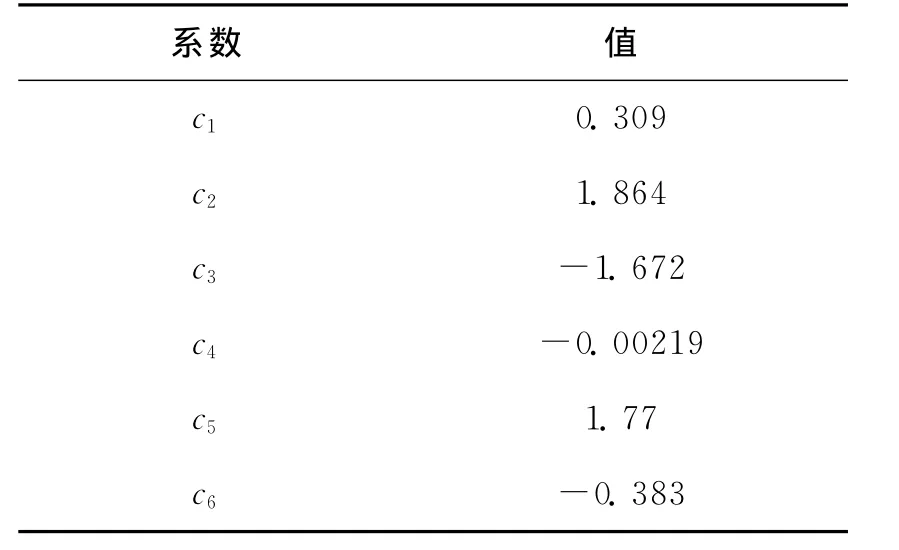
表1 方程（1）（修正的北美西部烈度预测方程）的系数

在图5中，我们进行了检查，以确保方程（1）（表1的系数）的新烈度预测方程对加州地区的实测DYFI烈度数据有良好拟合。仅对于Ipred≥2.5的那些段，我们画出了分段烈度数据的残差。如果我们考虑所有M≥3.5的地震事件，在距离上平均残差趋势就会小。如果仅考虑M≥4的地震事件，在所有的距离上平均残差一般在0的标准误差之内；例外是在10到30km和超过100km的距离上，烈度被略微高估了0.2个单位。我们可以得出这样的结论：北美西部修正的烈度预测方程和加州地震的实测烈度数据达到了令人满意的一致。注意，对于M＞4、Ipred＞2.5的地震事件，预测方程残差的标准偏差是0.5个单位。

这就出现了简单等权重方法是否在大震近距离产生切合实际烈度的问题。为核实这个问题，我们检查了从DYFI网站获得的M≥5.5地震事件（1971年以后可用）的加州地震最大烈度。我们删除了近海事件和墨西哥的事件（这些事件的近距离MMI不可靠），剩下了20个地震事件。根据Boatwright和Bundock（2005）的文章，我们增加了1906年旧金山M7.8地震的最大烈度。图6示出了这些较大地震DYFI的最大烈度与根据提出的新烈度预测方程预测值的比较。重要的是要知道描绘的点代表最大观测烈度，而预测线是平均场地条件的中值烈度（0震中距处）。因此我们不预期该烈度预测方程能拟合最大观测烈度，只期盼定性的一致性。特别是我们注意到，0距离处烈度预测方程增加的趋势匹配了最大历史烈度指示的总趋势。而且，正如我们预期的那样，最大观测烈度往往平均大于烈度预测方程预测的中值。归结起来，我们可以得出这样的结论：对于大震事件，烈度预测方程的最大值与历史烈度数据比较一致。从图6得出的一个令人感兴趣的推论是烈度似乎和地震动幅值的饱和程度不同。

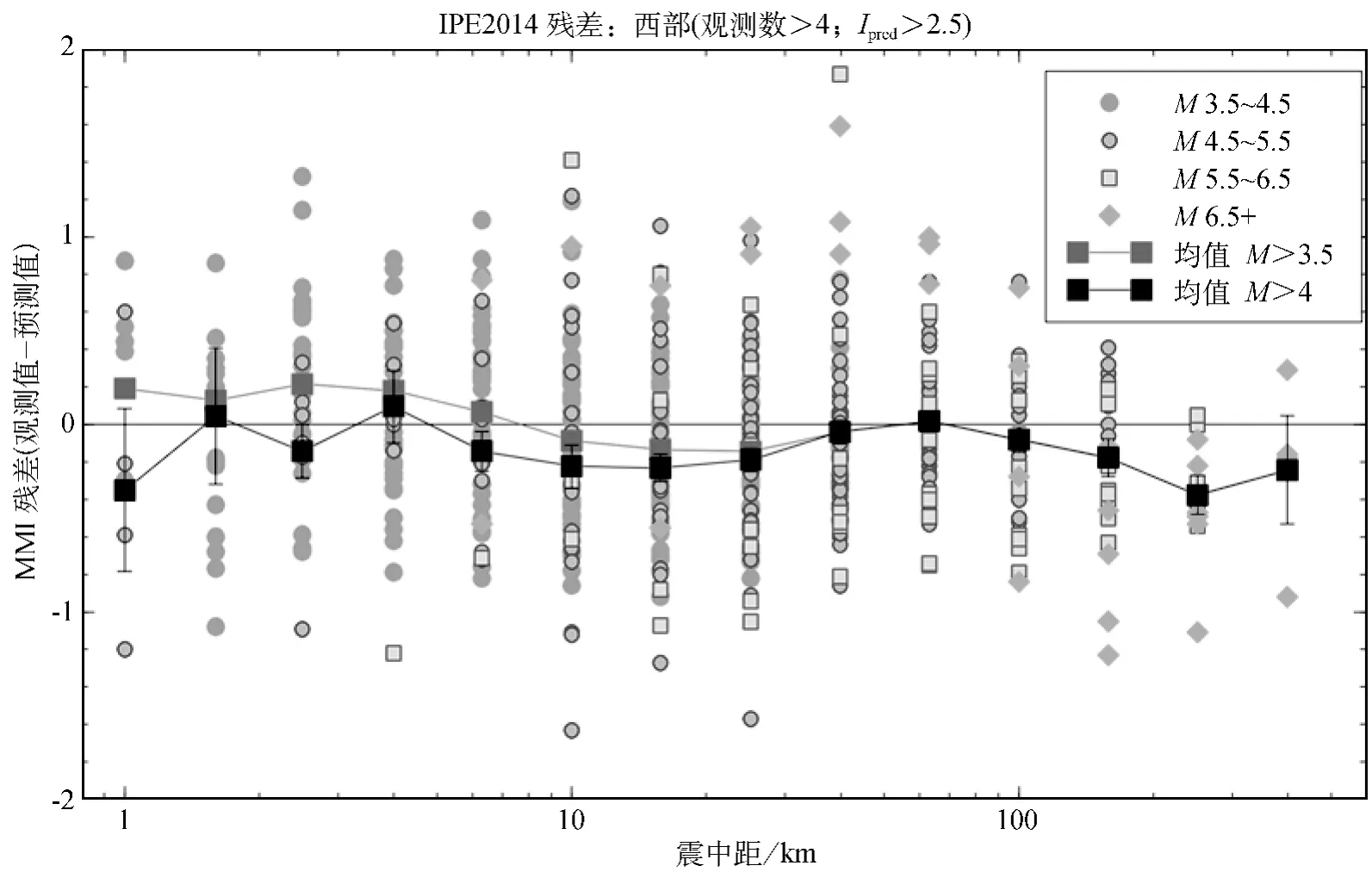
图5 北美西部的新烈度预测方程（IPE）的残差（观测值－预测值）。符号表示由震级范围标识的事件的分段残差，方块表示M≥3.5的所有事件的平均误差。带有误差棒的方块表示M≥4的所有分段烈度数据的均值和标准误差。该图的彩色版仅适应于电子版本

图6 表明，尽管最大观测烈度很分散，但我们还是可以看出新地震动预测方程没有高估大震事件的最大烈度，更可能的是或许低估了最大烈度。

回想一下，我们导出的北美西部烈度预测方程代表了国家地震减灾计划C类平均场地条件（VS30≈450m／s）。假定不同的VS30值，我们可以协同W12地震动烈度相关方程使用Boore等（2014）地震动预测方程计算其他场地条件的烈度值的预期变化。一般来说，因为较软的土层对地震动有更大的放大作用，我们能想到在较软的土层上会有较高的烈度。比如，如果我们假定Boore等（2014）中的VS30＝200m／s，对于产生线性场地响应足够远的地震事件（如在100km为M5.5到7.5），我们能够推断出（通过W12）其烈度比我们用450m／s参考场地条件计算的烈度高约0.5个单位。类似地，对于弱震动，岩石类场地上（700到800m／s）的预测烈度会比VS30＝450m／s的场地约小0.5个单位。然而对于强震动，非线性减弱了软土层区域产生更高幅值的趋势。这样，对于近距离（1.5km）的M5.5到7.5的事件，我们在很宽的VS30（180到550m／s）范围预测了很小的烈度差异（＜0.2个单位）；坚硬场地（700到800m／s）会有约低0.5个单位的烈度。这些估计值仅考虑了场地刚度对震动幅值的影响，而烈度或许还受其他因素的影响，比如较软土层趋于产生较大的不均匀沉降，这可能增加破坏。这样我们有理由推测，软土层上的烈度或许高于我们的烈度预测方程给出值0.5～1个单位，岩石类场地上的烈度或许低于我们的烈度预测方程给出值0.5～1个单位。

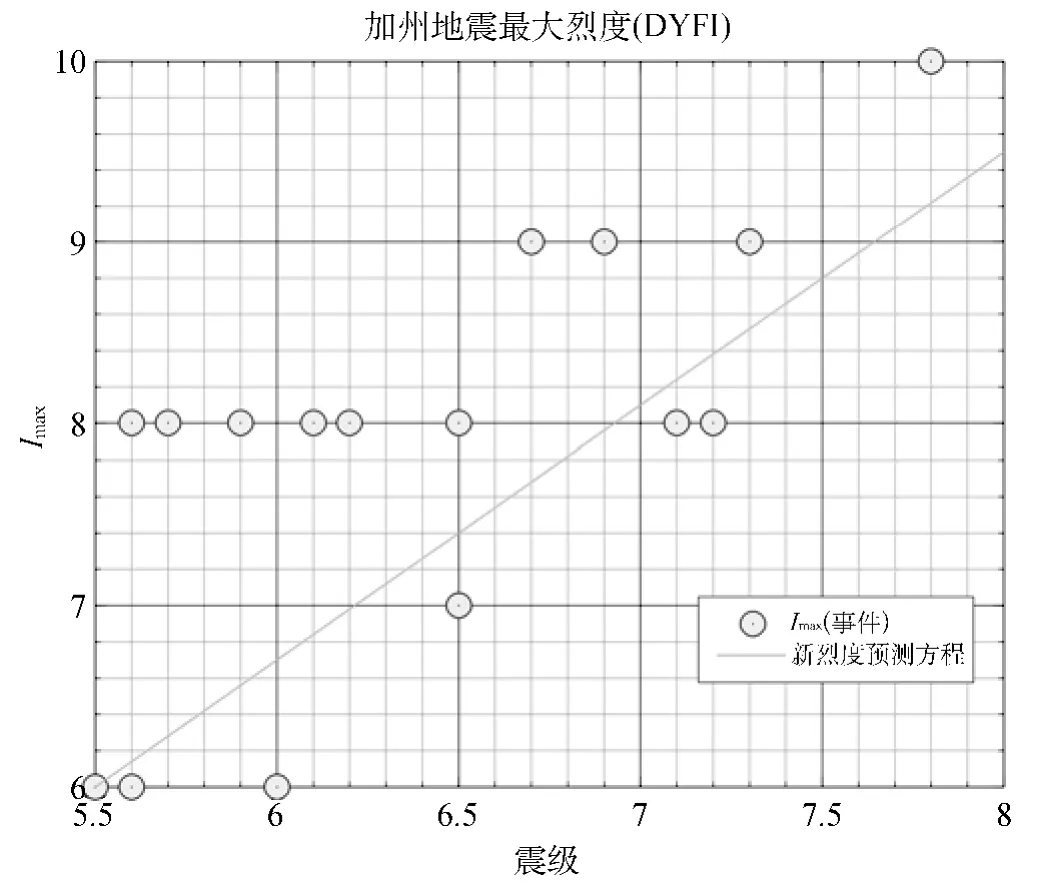
图6 从DYFI网站获得的加州地区M≥5.5地震事件（符号）的最大观测烈度和由北美西部新烈度预测方程预测的震中烈度值（线）的比较（由于烈度预测方程试图代表中值水平，最大观测烈度值一般应该超过烈度预测方程的值）。该图的彩色版仅适应于电子版本

2 北美东部烈度预测方程的导出

我们遵从参考经验方法（Atkinson，2008）的概念，通过检查美国东部地震相对于上节导出的北美西部烈度预测方程的烈度残差获得了东部地区的烈度预测方程。我们这么做的原因是，在美国东部地区地震动预测方程和地震动烈度相关方程在人们最感兴趣的震级－距离范围都没有受到数据的良好约束。总的说来，根据烈度观测结果（例如，Atkinson and Wald，2007）和地震动预测方程 概 念 （例 如，Atkinson and Hanks，1995），我们可以预期美国东部的地震比震级相同的北美西部地震会具有更高的近源烈度，其部分原因是由于应力降较高。而且，在区域距离上，由于地壳衰减较低，美国东部的烈度衰减会更慢；由于直达波和来自莫霍间断面的超临界反射和绕射波的联合作用（Burger et al，1987），在中远距离处可能会出现显著的 “莫霍面反弹”效应。因此当我们检查美国东部地震相对于由加州地震事件导出的烈度预测方程的烈度残差时，我们预期可能看到偏移和距离趋势。我们可使用这种偏移和趋势计算校正因子，使我们能够导出基于西部烈度预测方程的东部烈度预测方程调整量。

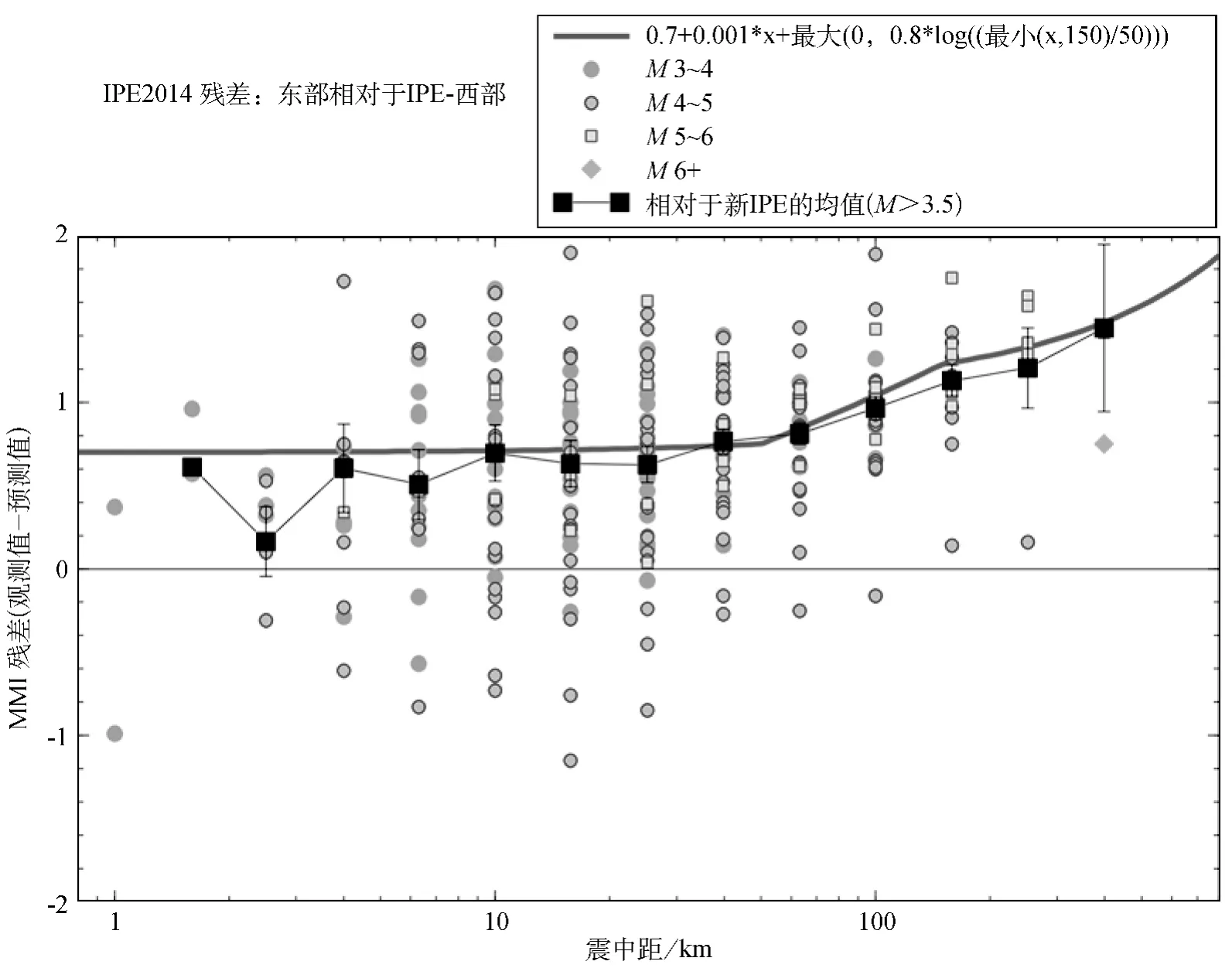
图7 相对北美西部烈度预测方程的美国东部M≥3地震事件分段烈度的地震烈度残差（观测值－预测值）（每段最少4个观测值），符号表示不同的震级范围。带有误差棒的方块表示M≥3.5事件所有分段值的均值和标准误差。粗线表示由0.7＋0.001 Depi＋max（0，0.8log（min（Depi，150）／50））给出的平均烈度残差。该图的彩色版仅适应于电子版本

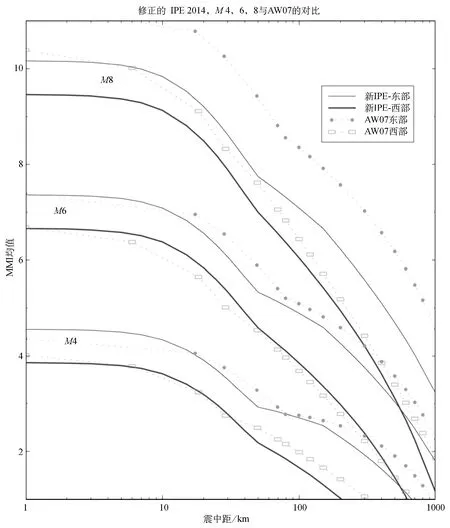
图8 对M4，6和8地震事件绘出的东部新烈度预测方程（IPE）（细线）和西部新烈度预测方程（IPE）（粗线）与AW07预测值（东部为圆圈，西部为方块）的对比。该图的彩色版仅适应于电子版本

在图7中，我们画出了东部地区的烈度残差（＝Iobs－IpredW），这里，对于M≥3.5地震事件，观测烈度是针对分段烈度数据给出的，每段至少有4个观测值，IpredW是使用北美西部烈度预测方程 ［由方程（1），使用表1的系数］预测的烈度。为了消除弱、远观测引起的偏差，我们在IpredW≥1.5的震级－距离段考虑了美国东部的数据。通过下面的推理，这等同于对加州数据使用了Ipred≥2.5的弱烈度截断。在加州，我们检查了绘制的烈度图，从而确定Ipred≥2.5的观测结果是无偏的（相对于方程）。在东部地区，通过检查绘制的烈度（或由AW07），可以观察到在东部地区I＝2.5达到的距离大约是西部相应距离的3倍 ［比如，一个M4地震事件在西部的有感（I＝2.5）距离约为40km，而在东部的有感距离是120km］。考虑到中等地震事件北美西部烈度预测方程的斜率，我们能够通过限定包含东部数据到IpredW≥1.5的震级－距离段实现适当的烈度截断。

如图7所示，用简单的函数很好模拟了东部的烈度残差，这个简单函数含有近距离偏移项、模拟莫霍反弹效应从50到150km的渐升项和解释东部地区较高区域品质因子的滞弹性衰减校正项。几乎对所有点，平均分段残差都在这个函数的标准误差之内。所以我们可使用下式估计美国东部地震事件的预测烈度：

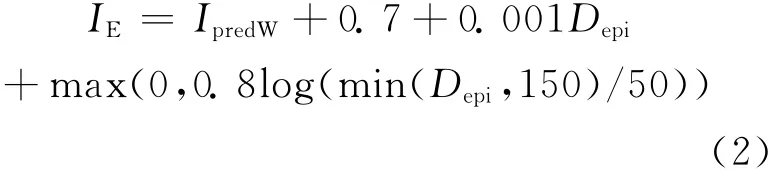
式中IpredW是使用方程（1）（表1的系数）得到的北美西部的预测烈度，Depi是震中距。需要说明的是，尽管为了方便起见，我们这里使用了震中距，但距离项只在远距离处（＞100km）变得显著，对于距离项，其他替代的距离量度大致也是等效的。因此，调整因子也可以用Dh代替Depi。在应用该校正因子后，美国东部地区的预测烈度平均残差接近于0，对于M＞3、IpredE＞2.5的地震事件，标准偏差为0.5。

3 讨论与结论

在图8上做了新烈度预测方程与AW07之间的对比。和预期的一样，总体上对中小地震事件，新烈度预测方程与AW07具有良好的一致性，但对高震级事件，特别是在近距离，预测的中值烈度较低。北美东部与北美西部之间衰减曲线形状的差异包括近距离偏移和莫霍面反弹效应引起的肩型抬升，这些反映了在DYFI数据中许多美国东部较大事件中看到的效应。我们得到的结论是：新烈度预测方程 ［方程（1）和（2）］在大的震级和距离范围上提供了北美东部和西部地震在平均场地条件下稳健且受到良好约束的中值烈度预测结果。

正如在引言中所述，最大可赋予的烈度值一般限制到10。因此，在实践中这些烈度预测方程的输出值应该被约束到不大于10。如果希望与DYFI一致，烈度实际上应该被限制到9.6，这是DYFI项目可获得的最大值。同样，最小可赋予的MMI是1.0；小于1.0的输出值应该被设为1.0。DYFI不赋予1.0和2.0之间的烈度值；因此如果希望一致，1.0和2.0之间的值应该四舍五入到最接近的整数（但是，由于前面讨论的低烈度偏差效应，对这些低烈度值应该谨慎）。这些烈度预测方程是使用加州和美国东部地区具有5～15km典型震源深度的地震数据导出的。要把它们用到其他地区，就需要适度谨慎，特别是对震源深度范围不同于本研究的地区。

数据与来源

本研究使用的 “你感觉到了吗”的数据可从美国地质调查局网站下载，网址为http：／／earthquake.usgs.gov／earthquakes／dyfi／（最 近 访 问 时 间2014年4月）。

Atkinson，G.（2008）.Alternative ground－motion prediction equations for eastern North America from a referenced empirical approach：Implications for epistemic uncertainty，Bull.Seismol.Soc.Am.98，1304－1318.

Atkinson，G.，and J.Adams（2013）.Ground motion prediction equations for application to the 2015 national seismic hazard maps of Canada，Can.J.Civil Eng.40988－998.

Atkinson，G.，and T.Hanks（1995）.A high－frequency magnitude scale，Bull.Seismol.Soc.Am.85，825－833.

Atkinson，G.，and D.Wald（2007）.Modified Mercalli intensity：A surprisingly good measure of ground motion，Seismol.Res.Lett.78，362－368.

Boatwright，J.，and H.Bundock（2005）.Modified Mercalli Intensity maps for the 1906San Francisco earthquake，U.S.Geol.Surv.Open－File Rept.2005－1135，11pp.，11electronic maps（http：／／pubs.usgs.gov／of／2005／1135／；last accessed September 2014）.

Boore，D.，J.Stewart，E.Seyhan，and G.Atkinson（2014）.NGA－West2equations for predicting response spectral accelerations for shallow crustal earthquakes，Earthq.Spectra doi：10.1193／070113EQS184M.

Bozorgnia，Y.，N.Abrahamson，L.Al Atik，T.Ancheta，G.Atkinson，J.Baker，A.Baltay，D.Boore，K.Campbell，B.Chiou，R.Darragh，S.Day，J.Donahue，R.Graves，N.Gregor，T.Hanks，I.Idriss，R.Kamai，T.Kishida，A.Kottke，S.Mahin，S.Rezaeian，B.Rowshandel，E.Seyhan，S.Shahi，T.Shantz，W.Silva，P.Spudich，J.Stewart，J.Watson－Lamprey，K.Wooddell，and R.Youngs（2014）.NGA－West2research project，Earthq.Spectra doi：10.1193／072113EQS209M.

Burger，R.，P.Somerville，J.Barker，R.Herrmann，and D.Helmberger（1987）.The effect of crustal structure on strong ground motion attenuation relations in eastern North America，Bull.Seismol.Soc.Am.77，420－439.

Dewey，J.，B.Reagor，L.Dengler，and K.Moley（1995）.Intensity and isoseismal maps for the Northridge，California，earthquake of January 17，1994，U.S.Geol.Surv.Open－File Rept.95－92，35pp.

Dewey，J.，D.Wald，and L.Dengler（2000）.Relating conventional USGS modified Mercalli intensities to intensities assigned with data collected via the InternetSeismol.Res.Lett.71264.

Hough，S.（2012）.Initial assessment of the intensity distribution of the 2011 Mw5.8Mineral Virginia earthquake，Seismol.Res.Lett.83，649－657.

Joyner，W.，and D.Boore（1981）.Peak horizontal acceleration and velocity from strong motion records including records from the 1979Imperial Valley，California，earthquake，Bull.Seismol.Soc.Am.71，2011－2038.

Power，M.，B.Chiou，N.Abrahamson，Y.Bozorgnia，T.Shantz，and C.Roblee（2008）.An overview of the NGA project，Earthq.Spectra24，3－21.

Wald，D.，V.Quitoriano，L.Dengler，and J.Dewey（1999）.Utilization of the Internet for rapid community intensity maps，Seismol.Res.Lett.70，680－697.

Wood，H.，and F.Neumann（1931）.Modified Mercalli intensity scale of 1931，Bull.Seismol.Soc.Am.21，277－283.

Worden，B.，M.Gerstenberger，D.Rhoades，and D.Wald（2012）.Probabilistic relationships between ground motion parameters and modified Mercalli intensity in California，Bull.Seismol.Soc.Am.102，204－221.