采用不同摩擦定律动态模拟断层阶跃

Kenny J.Ryan David D.Oglesby

0 引言

就几何形态和介质属性而言，整个地球的地震断层都相当不均匀，确定这些属性如何影响地震破裂是地震学正面临的挑战。这种几何复杂性之一便是断层阶跃：地球表面彼此断错的一组不连续的、平行的断层段。在这些断层段之间的走向上也可部分重叠、不重叠或间断。具体说，走滑断层阶跃是两个或多个走滑断层段组成的这种系统。断层段走向之间的水平断错量称为阶跃宽度。自然界中观测到的断层阶跃宽度从厘米级到千米级（Vedder and Wallace，1970；Bartlett et al，1981）。由于地震矩正比于破裂面积，因此地震破裂是终止于断层阶跃还是跨越断层阶跃就成为确定这种地震事件最终震级的关键。各个断层段的强度及其动态应力降可能依赖于断层段的构造成熟度（例如，Scholz et al，1986；Manighetti et al，2007）。Manighetti等（2007）特意观察了一系列大的多段破裂的地震（MW≥6）并证实了沿各个断层段应力降的变化，观测到不成熟的断层段有较大的应力降。断层段间应力降的变化可影响阶跃的动态破裂模型。地震动的分布也强烈依赖于所破裂断层的类型。1992年加利福尼亚兰德斯MW7.2地震是这种情形的极好例子——至少破裂了5条向北呈右阶几何形态的主断层，并且是美国本土40年以来的最大地震（Sieh et al，1993）。过去30年对断层阶跃已有很多基准研究，包括数值研究（例如，Segall and Pollard，1980；Harris and Day，1993；Kase and Kuge，1998；Duan and Oglesby，2006）和观测研究（例如，Wesnousky，1988；Sieh et al，1993；Lettis et al，2002； Wesnousky，2006）。这些研究表明地震很容易被较大的阶跃宽度（阶跃系统中断层段的断错距离）所阻止。特别是，野外观测表明地震破裂可能不会跨过阶跃宽度大于5km的压性阶跃或阶跃宽度大于8km 的张性阶跃（Wesnousky，1988；Knuepfer，1989）。很多断层阶跃的数值研究检验了走滑阶跃的两种基本类型：压性和张性阶跃（Segall and Pollard，1980；Harris et al，1991；Harris and Day，1993；Kase and Kuge，1998；Harris and Day，1999；Duan and Oglesby，2006；Oglesby，2008）。压性阶跃的断层滑动导致断层段间的区域受挤压，而张性阶跃的断层滑动则导致断层段间的区域受拉张。两种类型均显示了地震破裂期间断错断层段之间产生动态应力强扰动。此外，阶跃系统中次断层段上破裂再起始的位置随该系统为压性还是张性而变化。起始一般发生在主断层段破裂终止之后（例如，Harris and Day，1993；Kase and Kuge，1998）。而且，无论数值研究还是观测研究，均显示停止相（由主断层的突然终止而引起的地震辐射）控制断层破裂能否跨越阶跃（Bernard and Madariaga，1984；Spudich and Frazer，1984；Oglesby，2008；Elliot et al，2009）。

因为地震涉及两个彼此相互滑动的断层面，因此摩擦是地震过程的固有部分。众所周知，地震由断层摩擦而储存的弹性能所引起。并且，摩擦系数一定程度上决定了破裂的动力学过程。前面引述的所有断层阶跃数值研究均采用了线性滑动弱化（SW）摩擦（Ida，1972；Palmer and Rice，1973；Andrews，1976）。然而，尚未利用诸如速率—状态依从摩擦的实验室导出的摩擦定律对断层阶跃的破裂属性作深入研究（Dieterich，1978，1979；Ruina，1983），该摩擦定律能对破裂起始和动力学提供更实际的表示。速率—状态依从（RS）摩擦定律受滑动速率和一个或多个状态变量的时间演化所控制，但一般正如同 Okubo（1989）、Dieterich和Kilgore（1994）及Bizzarri等（2001）所指出的在滑动初始时表现出有效滑动弱化行为。假设接触随成熟而变强，速率—状态依从摩擦定律公式中的状态变量可被认为与凹凸体（断层不断滑动的小接触面）的强度和滑动速度过程有关。因为速率—状态依从的摩擦参数已在实验室实验中给出，它们为模拟地震破裂动力学提供了合理的依据。对一给定参数，摩擦定律可用地震破裂初始时的有效滑动弱化曲线来描述。与具有相同应力降的低缓滑动弱化曲线相比，陡峭滑动弱化曲线表示破裂开始和传播需要相对少的破裂能。很多实验研究，包括高速实验，均显示出非线性滑动弱化曲线（Dieterich，1979；Tsutsumi and Shimamoto，1997；Prakash，1998；Prakash and Yuan，2004；Goldsby and Tullis，2002；Tullis and Goldsby，2003a，2003b；Hirose and Shimamoto，2005）。

有些动态破裂模拟研究包括强速率弱化摩擦（例如，Zheng and Rice，1998；Rojas et al，2009），根据的是速率—状态依从的摩擦构架（例如，Okubo，1989），其中，断层面某点的剪应力随滑动速率大幅下降。众所周知，断层附近发现较少的假玻璃熔岩，很可能是由于低摩擦的原因（Sibson，1973）。强速率弱化摩擦可随滑动速度增加，摩擦系数大幅下降，因而可模拟急骤加热或微小凹凸体的熔融（Rice，1999，2006；Beeler and Tullis，2003；Beeler et al，2008）。强速率弱化摩擦行为已在Tsutsumi与 Shimamoto（1997）、Prakash（1998）、Prakash与Yuan（2004）、Goldsby与Tullis（2002）、Tullis与 Goldsby（2003a，2003b）和Hirose与Shimamoto（2005）的高滑动速率（≈1m／s）实验室实验中观测到。上述实验研究结果与大幅弱化发生时的速度为0.2m／s的量级水平一致，而静、动摩擦系数的范围分别为0.6～0.9和0.2～0.3。在地震模拟中采用这些数值有助于我们约束沿断层（Nielsen and Olsen，2000）和阶跃地区这种弱化机制的影响。

摩擦弱化的函数形式与地震破裂能量收支直接相关（例如，Andrews，1976；Kanamori and Rivera，2006）。地震的总能量可分成三类：破裂能量、抵抗摩擦而消耗的能量和地震辐射能（见图2）。有效滑动弱化距离d0是破裂过程中应力下降的滑动距离（Rabinowicz，1951）。因为应力－滑动曲线的形状随摩擦定律不同而不同，所以模拟地震的能量收支与摩擦参数直接相关。

地震破裂速度已被证实为地震学中极其重要的一个方面，它与地震的关键方面诸如滑动、应力降和地震动等直接相关。以超剪切破裂速度传播的破裂能力尤为重要，因为这种破裂可产生相对较大的平行断层的质点运动，并且所产生的马赫锥携有远离断层的大应力和质点速度（例如，Dunham and Ar－chuleta，2004；Bernard and Baumont，2005）。根据对1979年英皮里尔谷地震、1992年兰德斯地震、1999年伊兹米特地震、2001年昆仑山地震和2002年迪纳利断层地震的多个观测推断出了超剪切破裂速度（例如，Archuleta，1984；Olson and Apsel，1982；Spudich and Cranswick，1984；Olsen et al，1997；Bouchon and Vallée，2003；Ellsworth et al，2004）。岩石实验显示了沿均匀界面（Rosakis et al，1999；Rosakis，2002；Xia et al，2004）和双材料界面（Xia et al，2005）的II型裂纹的超剪切转换。超剪切破裂传播也在很多计算和理论研究中有预测和探讨（例如，Andrews，1976；Day，1982；Harris and Day，1997；Cochard and Rice，2000；Madariaga and Olsen，2000；Fukuyama and Olsen，2002；Dunhamet al，2003）。Burridge（1973）和Andrews（1976）证实在破裂前缘前面传播的剪切波能使裂纹尖部的应力增加到屈服水平，形成沿断层界面以超剪切速度扩展的“子”裂纹。对于II型断裂，在能量方面有利的条件下，破裂速度限制为Vrupt≤VRayleigh或者Vrupt≥Vshear（即介于瑞利波与剪切波速之间的破裂速度是不允许的）。Liu和Lapusta（2008）研究表明 “有利的非均匀性”，如先前存在的亚临界裂纹或高预应力的小片区，可促进II型裂纹从低于瑞利波速变化到超剪切速度（就像被主裂纹驱动为超剪切速度的次裂纹）。Dunham（2007）表明，沿断层走向的断裂能量和应力降的变化可导致超剪切转换。此外，Dunham（2007）认为超剪切转换的长度对有效滑动弱化距离曲线敏感，具体到采用的摩擦公式就是，由于临界起始长度较小，随着滑动应力减小越快，转换长度就越小。

图1 用动态有限元程序FaultMod得到的二维断层几何模型图（Barall，2008，2009）。箭头表示区域应力场。注意次断层段的位置意味系统是压性（上）还是张性（下）。星号表示起始区。断层段的长度和重叠部分均固定。阶跃宽度可变。对任何给定的模拟，只存在一条次断层（蓝色）（原图为彩色图——译注）

表1 低应力模型1）

之前探讨摩擦参数对破裂动力学影响的研究重点关注平面断层，对非平面断层动力学的研究几乎全部采用简单的滑动弱化摩擦。很少有模拟研究看到由复杂断层几何形态（如断层阶跃）引起的超剪切转换（例如，Oglesby et al，2008）。在这种研究中采用多种类型的摩擦公式可对有关断层阶跃的跨越能力和破裂速度的结果提供一般性表述，或至少提供不同摩擦参数中这些参数的相对值。解析几个不同的摩擦公式有助于说明结果的稳健可靠性。

表2 高应力模型1）

1 方法

我们采用二维有限元法（FEM）程序FaultMod（Barall，2008）模拟了压性与张性环境下沿断层阶跃的摩擦界面的II型动态破裂（图1）。二维地震破裂模型可对几何参数提供合理的检验，并可很好地扩展为三维情 况 （例 如，Harris and Day，1993，1999）。所有模拟均约束为只允许平行于平面的运动（平面应变）。破裂约束为发生在两个平行断层段的一个或两个上。我们假设介质为均匀线弹性材料。每个断层段长为50km，两段之间的重叠部分长7km。无论压性还是张性环境，该重叠长度足以使破裂在次断层上再起始。阶跃宽度，或称断错距离，是可变的，可使我们确定在我们的参数设置下沿断层阶跃破裂可跨越（垂直于断层走向）的最大距离。FaultMod程序自动生成网格，在不损失计算精度的前提下采用随远离断层系统网格尺寸加倍的网格来减少计算资源，并在南加利福尼亚地震中心与美国地质调查局的破裂基准问题中得到有效应用（Barall，2009；Harris et al，2009）。该程序包含人工黏性阻尼（Dalguer and Day，2007）和算法阻尼以帮助沿网格边界的阻尼振荡和能量吸收边界条件避免模型边界的人为效应。我们分别考虑了相对小和大绝对应力场及小和大应力降对系统摩擦的影响（表1和表2）。大绝对应力场约为小绝对应力场的5倍。

我们比较了4种摩擦公式，包括线性滑动弱化（SW）摩擦和3种速率—状态依从摩擦：衰变定律（RS－AL）、滑动定律（RS－SL）和强速率弱化滑动定律（RS－SRW）。线性滑动弱化摩擦的判据如下（Ida，1972）：

式中，μ为摩擦系数，δ为累积滑动，d0为摩擦系数从静态值降为动态值的滑动距离，被称为是有效滑动弱化距离。对于滑动弱化摩擦，摩擦系数随滑动线性下降。

速率—状态依从摩擦的一般形式如下（Ruina，1980，1983；Linker and Dieterich，1992）：

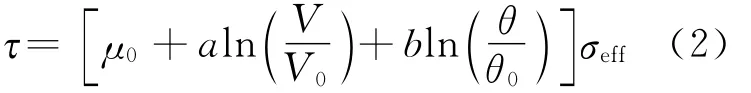
式中，μ0代表摩擦系数的恒定参考值，a和b是由实验室实验估计得到的本构参数；V0和θ0分别是滑动速率和滑动面状态的参考值，因此当V＝V0和θ＝θ0时，摩擦系数为μ0；θ是时间单位，理论上代表某一滑动速度下接触的强度；σeff为有效正应力。括号内的项是摩擦系数。注意，滑动速度V增加，相应的摩擦也增加，并随着滑动速度增加，凹凸体处于接触状态的时间更短，使得θ变小，最终摩擦力降低。

遵循Barall（2009）的做法，我们采用公式（2）括号内的项变换后的形式，对于很小的滑动速度，它也不会变为奇异：

对于地震学方面的滑动速度，这种速率—状态依从摩擦定律形式非常接近于公式（2）。注意公式（3）的右边当ψ＝bln（θ／θ0）时具有公式（2）中的有效摩擦系数形式。概念上，ψ可代表接触强度。

对于衰变定律，状态变量根据方程（4）演变：

速率—状态相依从的衰变定律的摩擦也随滑动相对线性下降（相对于滑动定律）。在衰变定律中，状态变量根据方程（5）演变：

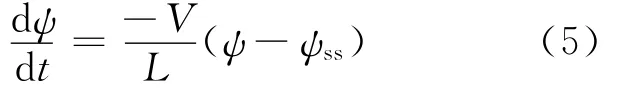
速率—状态依从的滑动定律随滑动具有初始陡峭上凹的函数形式（Ruina，1980，1983）。衰变定律（公式4）和滑动定律（公式5）均可归纳为稳态滑动的标准公式：

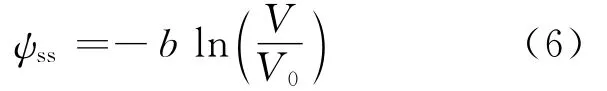
强速率弱化滑动定律，显著不同于滑动定律，包括下列稳态方程（例如，Rice，1999，2006；Beeler and Tullis，2003；Rojas et al，2009）：

式中μs为强摩擦系数，μw为弱摩擦系数，Vw为弱化（摩擦强度）发生的速度。

由Palmer和 Rice（1973）及 Andrews（1976）定义的沿破裂特定位置的有效破裂面能量（EFSE）为：

式中，τ为剪应力，δ为累积滑动。许多数值研究将有效破裂面能量限制为在破裂面上相对恒定；然而，这一假设是不现实的。比如，Andrews（2005）指出，有效破裂面能量（因而还有d0）沿破裂面并不恒定，并可由于地震动力学过程而增加。断层损伤区的非弹性变形也对地震的能量收支有贡献（为数值简化，它通常与破裂能量混在一起）。应该指出的是，由于非线性摩擦关系中d0选择的主观性，对有效破裂面能量的估计可能也有些主观（例如，Bizzarri and Cocco，2003；Rojas et al，2009）。众所周知，动力学模拟呈现出滑动应力的下冲或过冲（例如，Mai et al，2006），并可导致有效破裂面能量的不确定性。对于滑动弱化摩擦，d0更易数值定义和实现。但是，速率—状态依从的摩擦参数的d0变量却不容易定义。在速率—状态依从的公式中，本构参数L代表特征滑动距离，与d0密切相关。Cocco和Bizzarri（2002）研究显示，L与d0为线性比例关系，对于速率—状态依从的衰变定律，典型参数d0／L比大约为15。

图2 地震能量划分简化示意图。实黑线表示断层上某点随滑移的剪应力。辐射能量密度中的灰三角表示破裂能量密度的全减法。注意该图表示普遍的非线性弱化曲线。不同的摩擦定律产生了不同的弱化曲线几何形状（原图为彩色图——译注）

为了将线性滑动弱化摩擦和速率—状态依从的摩擦公式进行比较，我们必须定义速率—状态依从公式中的d0。这样，我们就可以使用通用的d0值，从而剥离公式本身的影响。对于速率—状态依从的定律，我们估计d0为大约98%的总应力降发生的距离。因为对每一定律，d0依赖于速率—状态依从公式中的本构参数（对给定的应力状态），即L，我们对每个与速率和状态相关的公式采用特定的L值以形成一个通用的有效滑动弱化距离。我们通过用速率—状态依从的摩擦公式处理模型，匹配了线性滑动弱化、衰变定律和滑动定律公式的最大和滑动剪应力，然后在线性滑动弱化摩擦框架下选出合适的静态和动态摩擦系数。对于速率—状态依从的参数，最大和滑动剪应力事先未知；但是，Bizzarri和Cocco（2003）表明，这些值可用确定动态滑动速度的剪切阻抗关系和状态变量的初始值来近似估算。因而，在本研究范围内，通过参数化速率—状态依从的关系就能模拟线性滑动弱化关系（尽管并未在此尝试）。图2显示简化的地震能量收支示意图以及它如何与摩擦定律的函数形式相关。我们肯定地指出，辐射的能量密度应被认为是整个断层的平均；单点的辐射能量密度不容易由应力—滑动弱化曲线确定，因为大部分断层是同时滑动的，并且有复杂的应力波相互作用。然而，破裂能量沿断层单点耗散，使其容易从模型中测量。注意，在均匀的初始条件下，我们所有模型的破裂能量在所有破裂点均大致为常数（即所有点的d0大致相同），但是除非另有说明，不同摩擦参数的破裂能量不必相同（即使有相同的d0）。图3中通过将低应力和高应力模型中所有摩擦公式中的应力绘制为滑动的函数，我们阐明了有效滑动弱化距离均等化的方法。注意在d0相同时，这些参数的破裂能量相当不同。而图4显示了破裂能量相等时的相同摩擦公式。因此，最大到d0的弱化曲线下的面积近似相等（＜3%的差异）。动力学模拟参数研究显示地震S比率：

式中，τy为屈服强度，τ0为初始加载应力，τf为最终滑动应力，控制平面断层上向超剪切速度转换的破裂能力（Andrews，1976；Das and Aki，1977；Day，1982）。地震S比率不仅对预示超剪切转换很重要，同时也有助于确定沿断层阶跃的最大跨越破裂长度（Harris and Day，1993）。对于二维模拟，S＝1.77是阈值，大于该值，破裂就不能形成向超剪切速度的转换（Andrews，1976）。对于介于0与1.77之间的值，有一个相关的转换长度Ltrans（例如，Xia et al，2004）：

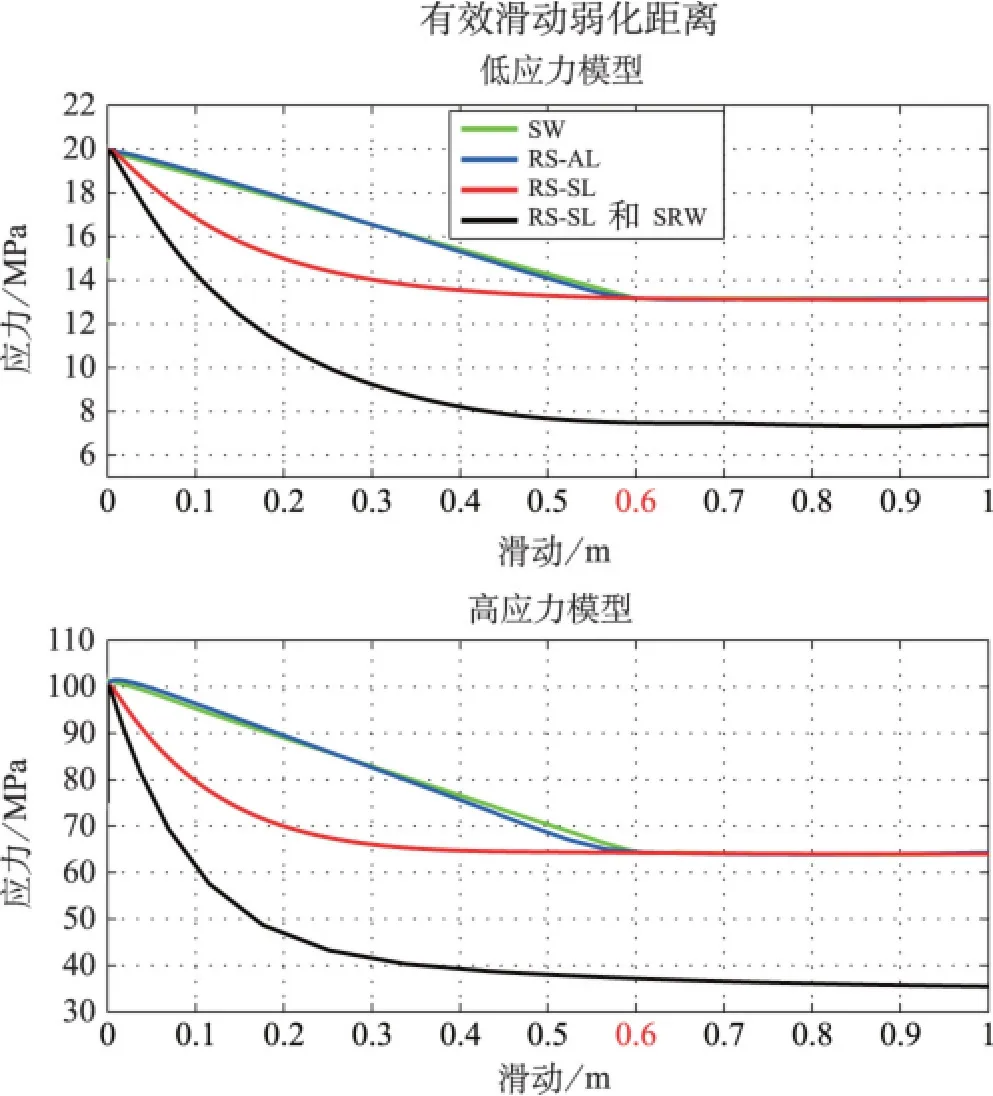
图3 低应力模型（上）和高应力模型（下）的有效滑动弱化距离曲线。为了对本研究中所有摩擦参数作有效对比，我们将每个摩擦公式调整为具有相同的有效滑动弱化距离。对于衰变定律和滑动定律的公式，我们将有效滑动弱化距离测量为断层段上某点完成98%的应力降的距离。强速率弱化滑动定律与滑动定律具有相同的L（速率和状态框架的长度参数）值。我们将所有模型的d0近似为0.6m。尽管这一判据具有主观性，但它为所有模型提供了共同的基础。注意相关破裂能量密度在不同摩擦参数间相应变化（即弱化曲线下的面积）（原图为彩色图——译注）

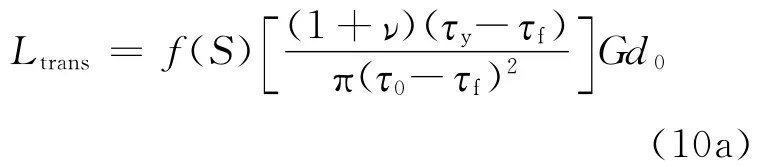
式中，

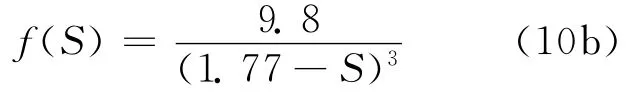
ν为泊松比，G为剪切模量。次瑞利波速破裂必须在达到超剪切速度前传播Ltrans的距离。

在我们的二维研究中，断层长度控制滑动持续时间，因此从沿走向边缘向内渗透的停止相控制破裂持续时间。因而，我们的模型代表大体为25km长的孕震区（Harris and Day，1993）。我们选取泊松比为0.25，因此α＝，其中α为P波速度，β为S波速度。为了准确求解破裂过程，有限元法的离散化必须能求解如下方面：（1）P波横穿最小单元尺寸的时间；（2）状态变量演化（对速率—状态依从的模拟）；（3）黏结区域的离散化（Palmer and Rice，1973）。为了检查，我们改写了Bizzarri和Cocco（2003）的方程（A3b）：

和一般条件（例如，Andrews，1985）

式中Δx为最小单元尺寸，Vrupt为破裂速度，Vave为节点从其达到屈服应力到滑动应力的时间段内的平均速度，α为P波速度，Δt为一个时间步长。此外，我们检查每个模型黏结区内的单元数量要为4个或以上，这是我们认为的求解过程的最小值。注意黏结区中单元数量最低的情形包含强速率弱化滑动定律模型。为了满足方程（11）和（12），我们的高应力模型沿断层有50m的网格增量，而低应力模型沿断层则有100m的网格增量。为具有可比性，我们在每个应力系统中的所有摩擦定律均采用相同的网格增量。此外，确定我们的模拟正确求解的可靠方法是比较不同时间的破裂前沿（Harris et al，2009）。因此，我们试算了低应力状态下50m单元和高应力状况下25m单元的强速率弱化滑动定律测试模型。我们发现距离起始中心20km远处较大增量与较小增量之间的破裂速度的百分比差异小于3%。

图4 具有可比破裂能量密度的低应力（上）和高应力（下）模型的有效滑动弱化距离曲线。为了使本研究所用的不同摩擦参数的破裂能量密度等同，相关的有效滑动弱化距离不可能总是相等。注意线性滑动弱化摩擦和速率—状态衰变定律的函数形式相似，因此可有相似的有效滑动弱化距离和破裂能量密度（原图为彩色图——译注）

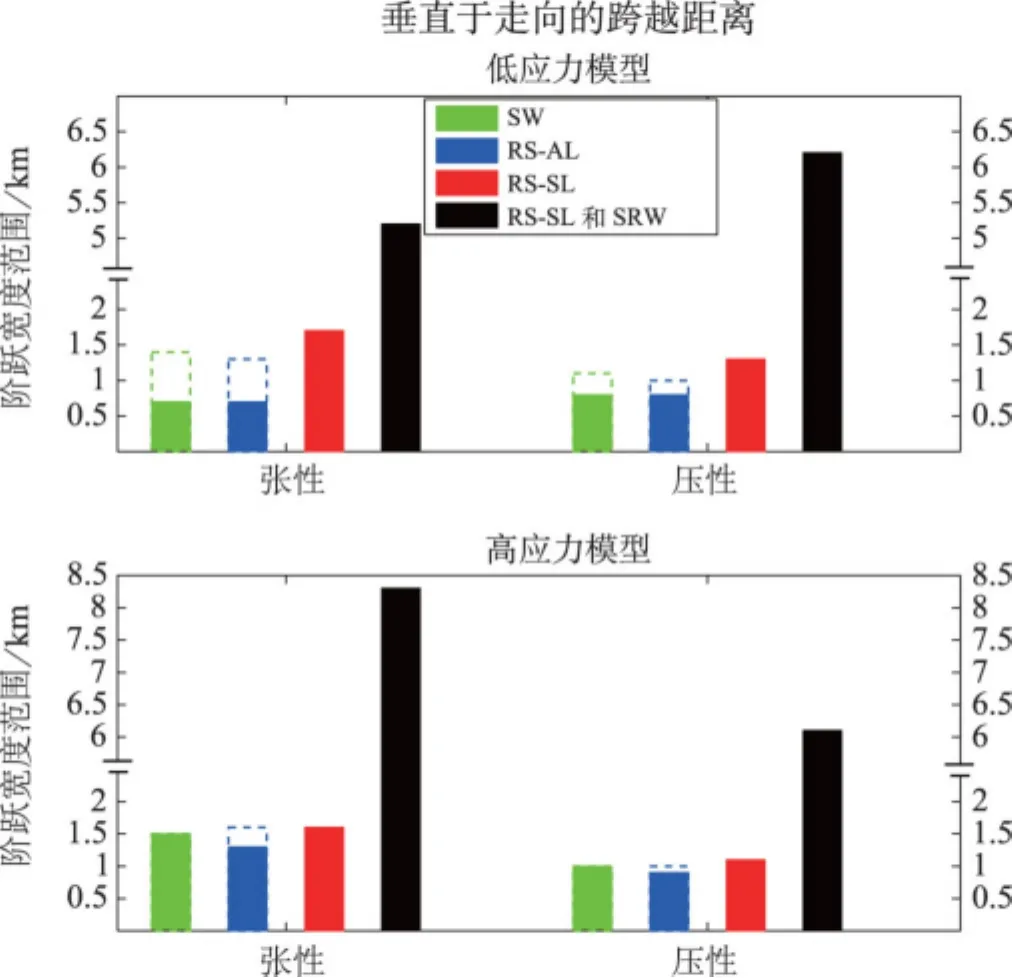
图5 低应力（上）和高应力（下）模型的最大跨越距离。图中显示了每一摩擦公式的垂直于走向的最大跨越破裂距离。实线区域表明具有等价滑动弱化距离的模型跨越距离最大（除了强速率弱化模型）。具有等价破裂能量密度的模型跨越距离最大，用虚线区表示。虚线区从不低于实线区。注意，y轴因为含强速率弱化摩擦的滑动定律模型跨跃距离很大而断开了（原图为彩色图——译注）

破裂在起始半宽度rn内通过主断层段中间的剪应力增强扩展区人工起始（见图1），低应力模型为3km，高应力模型为0.6km；随后允许破裂根据摩擦公式自发传播。低应力和高应力模型中的起始区均很大，足以限制离散化的影响，并且成比于（μd0）／（τy－τ0）， 其 中 μ 为 剪 切 模 量。 因此，低应力模型的rn是高应力模型的5倍。尽管本研究未关注起始过程的细节，但我们仍尽量限制起始区的大小以限制人工起始对破裂过程的影响。起始区大小如何影响沿断层阶跃的破裂属性尚需进一步的研究。

2 结果

本节中，我们首先基于具有等价有效滑动弱化距离d0的各种摩擦参数讨论最大破裂跨越距离。在第二小节中，我们重点讨论3个具有等价破裂能量的摩擦参数（不保证具有等价的有效滑动弱化距离）下的最大跨越距离。最后，我们报道之前未曾见到的超剪切破裂转换模式，它在断层阶跃系统中破裂从主断层跨跃至次断层时发生。

2.1 用等价d0比较不同摩擦参数

图6 当有效滑动弱化距离和摩擦系数保持恒定时，应力扩大后的线性滑动弱化曲线导致地震辐射密度与破裂能量密度之比变大（原图为彩色图——译注）

本研究的主要目的是直接对比断层阶跃地震破裂采用的多种不同摩擦参数。对比其他等效模型的一个方法是将上述各个摩擦公式中的有效滑动弱化距离d0设为相同。在d0相同的假设下，我们发现在断层阶跃区内不同摩擦定律之间破裂特性有显著差异。我们发现对于相同d0，无论压性还是张性阶跃系统，与等效衰变定律模型或线性滑动弱化模型相比，滑动定律模型使破裂跨越的阶跃宽度更大（图5）。滑动定律和线性滑动弱化模型就最大跨越距离来说十分相似，因为它们具有非常相似的弱化曲线函数形式。但是，滑动定律与衰变定律和线性滑动弱化模型相比，弱化曲线更为上凹，破裂能量更小。因此，它使主断层段释放更多的地震波能量，且沿次断层段起始破裂所需的临界片区尺度较小。因此，根据我们的判据，采用滑动定律时次断层段的二次起始更容易发生。由于应力降更大，以及相应的地震波能量也更大，强速率弱化（RS－SRW）模型能够跨越很大的阶跃宽度（大于7km）。总的来说，与低应力模型相比，高应力模型采用滑动弱化、衰变定律、滑动定律不同摩擦定律间的最大跨越距离的差别较小（图5）。我们将这一效果归因于随滑动增加地震的破裂能量与总势能之比的缩小。图6说明了这种效果。假设屈服剪应力接近于初始剪应力，上述所有模型采用了相同的d0，破裂能量与地震波能量之比和d0与总滑移量之比近似成比例。然而，高应力模型的总滑动量远大于低应力模型。换言之，虽然它们具有不同的函数形式，但高应力模型中地震辐射能量与破裂能量之比却增加，导致对破裂动力学（即最大跨越距离）产生相似效果的不同摩擦公式。我们承认，低应力状态的衰变定律、滑动弱化和强速率弱化滑动定律模型，压性阶跃的最大跨越距离比张性阶跃大，这与之前的一些研究（例如，Harris and Day，1993）不同，可能是由于应力状态不同所致。

2.2 用等价破裂能量比较不同摩擦参数

我们发现还有其他方法来比较不同摩擦定律（如用相等的有效滑动弱化距离）。d0相等时，我们将最大破裂跨越距离的不同归因于摩擦定律的函数形式和相关的能量收支。为测试分离破裂能量后函数形式的单独影响，我们采用衰变定律、滑动定律及滑动弱化摩擦模拟了破裂能量相等的地震破裂（图4）。注意，我们在这里未考虑强速率弱化公式，因为它是滑动定律的一种特殊形式，且有完全不同的能量收支。将所有破裂能量缩放为先前滑动定律模型的破裂能量［方程（8）中取d0为0.6m计算滑动定律模型的破裂能量］，滑动弱化与衰变定律的最大破裂跨越距离的不同相对于滑动定律模型是十分小的（图5）。因此，与每一摩擦定律相关的破裂能量对最大跨越距离具有一阶影响，特别是低应力的情况。由于我们的网格分辨率，无论高应力模型还是低应力模型，50m与100m网格尺寸的最大跨越宽度的差异并不显著。高应力模型表明，除强速率弱化滑动定律模型外，无论使用哪种摩擦定律，最大破裂跨越距离都可以非常相似。虽然对最大跨越距离的主要影响来自于破裂能量，但每个摩擦定律的函数形式仍然影响最大跨越距离，尽管这一影响并不强。这一结果与数值模拟研究一致（Dunham，2007），后者研究显示滑动弱化曲线的初始斜率可确定临界起始尺度（即，像滑动定律的陡峭初始斜率仅需要较小的起始区使破裂传播到起始区以外）。全面了解不同摩擦定律间的变化还需要进一步深入的研究，尤其是包含断层外损伤区域或沿断层可变破裂能量的更为复杂的能量收支。

2.3 作为超剪切转换机制的断层阶跃

对本研究中的高应力模型，我们发现对于特定参数，在次断层段的阶跃范围内存在超剪切转换。无论是张性还是压性环境，超剪切转换发生于等于或大于某一最小断层阶跃宽度。破裂向超剪切速度的转换似乎有些不可思议，因为根据标准的Burridge－Andrews机制，我们的初始条件原则上阻碍模型超剪切转换。这些模型的地震S比率设为2.6，大于1.77（该值时单断层二维模型不能发生超剪切转换）。因此，超剪切转换机制是之前未曾观测到的，它与断层几何形态和破裂跨越过程有关。主断层段破裂产生的动态波在次断层段破裂前改变了其应力场，使剪应力增加，正应力减小，从而引发了次断层段的超剪切破裂。对于衰变定律、滑动定律、线性滑动弱化摩擦公式，在断层阶跃的破裂延迟之后，超剪切转换优先沿压性和张性环境发生。强速率弱化的滑动定律模型之所以产生超剪切破裂，是由于较大的应力降导致了较低的地震S比率。显示出从主断层段到次断层段的超剪切破裂的模型比没有显示超剪切破裂的模型表现出从主破裂结束到次破裂开始间的更长的时间延迟。时间延迟越长的模型阶跃宽度越大。因此，为使超剪切转换发生，需要一个相应的最小阶跃宽度。对于压性环境，当d0相同时，维持次断层段上超剪切破裂所需的最小阶跃宽度分别是线性滑动弱化摩擦为0.6km，速率—状态依从的衰变定律为0.6km，速率—状态依从的滑动定律为0.7km。所有最小值以上的阶跃宽度均能维持整个次断层段长度的超剪切破裂（除非破裂不能跨越至次断层段）。然而，张性环境下超剪切破裂的出现似乎不太系统，尽管它们也存在超剪切转换所需的最小阶跃宽度，却没有可辨别的模式（如并非所有最小值以上的阶跃宽度必然维持超剪切破裂速度）。最终，这一效应很可能取决于起始区附近的地震S比率和沿走向的Ltrans的变化。我们强调的是，如图7所示，无论是压性环境还是张性环境，再起始均发生于正应力减小的区域。

我们发现，使次断层上产生超剪切速度转换的破裂能力与再起始区域内地震S值的空间分布有关。图7为次断层段破裂前的地震S比率图。图7a为压性环境下采用衰变定律摩擦的阶跃宽度为0.4km的例子；在此情况下，破裂不能维持超剪切速度。图7b为压性环境下阶跃宽度为1km的另一实例——次断层再起始后快速转换（并保持）为超剪切速度。为了运行Burridge－Andrew超剪切转换机制，破裂必须在裂纹尖端前沿的S波应力能激起超剪切破裂之前传播Ltrans的距离。次断层上每点的Ltrans值在图中给出。对于次断层段上保持超剪切破裂的情形（图7b），再起始区域附近的S值和Ltrans值小。因此我们看到，为使超剪切破裂覆盖整个次断层，超剪切S值（小于1.77）只需在包含再起始点的小区域（但比临界裂纹长度大）内发生。换句话说，如果减小的Ltrans值小于等于沿走向减小的Ltrans区域的宽度时，超剪切转换发生。例如，如果在宽度大于1km的区域Ltrans为1，那么当自维持滑动发生时超剪切转换便发生。这是图7b的情形。相反，图7a中（无超剪切转换），当成核区域周围的S小于1.77时，Ltrans值仍然很大，阻止了超剪切转换覆盖整个次断层长度。一旦破裂开始以超剪切速度沿次断层段扩展时，它满足■2β＜Vrupt＜α，这与 Andrews（1976）预测的一样。

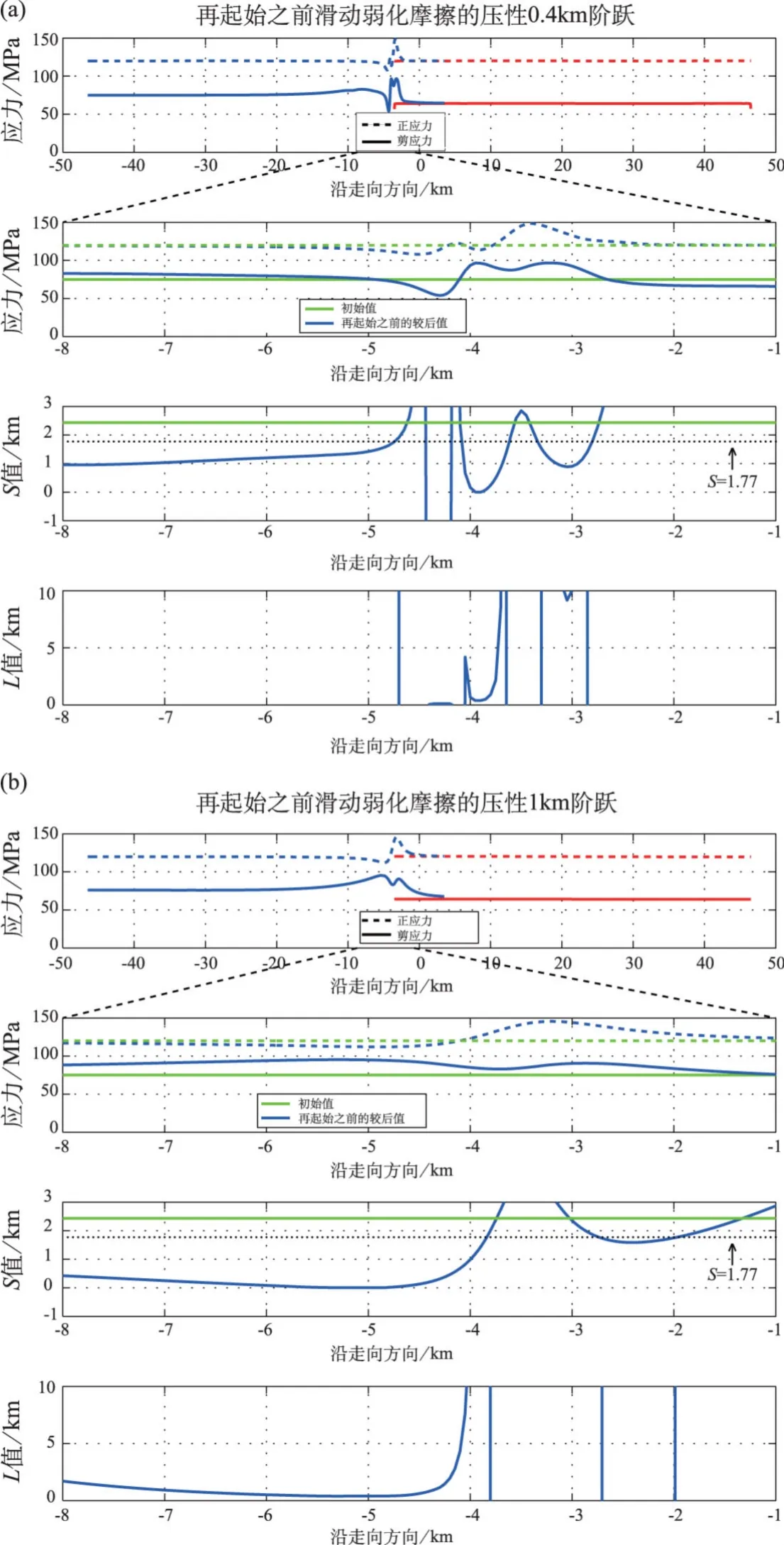
图7 （a）滑动弱化摩擦下0.4km压性阶跃的次断层段再起始前的应力快照（第一和第二行）。－8km至－1km的S比率和Ltrans值。再起始发生在沿走向的－3.9km处（第三和第四行）。沿断层延长段的S值和Ltrans值不够低，不能产生次断层段持续的超剪切破裂。（b）滑动弱化摩擦下1km压性阶跃次断层段再起始之前的应力快照（第一和第二行）。－8km至－1km的S比率和Ltrans值。再起始／超剪切扩展开始于沿走向的－5km处（第三和第四行）。沿断层延长段的S比率和Ltrans值足够低，产生了次断层段的持续超剪切破裂。（c）衰变定律下0.7km压性阶跃的特征超剪切转换的平行断层走向的速度。起始区用黑色星号表示。次断层段速度大幅增加。第一段破裂结束与第二段破裂开始间有约为15s的延迟。此外，在38.8s处标出了超剪切（S－S）马赫锥、P波前沿和紧随超剪切破裂的次瑞利（S－R）滑动脉冲（原图为彩色图——译注）

图7 c为压性环境下0.7km阶跃宽度的典型超剪切转换。一旦破裂达到超剪切速度，我们看到平行于断层有更大的速度。值得注意的是，从主断层段破裂结束到次断层段破裂开始有相当大的延迟（≈15s）。一旦发生再起始，超剪切破裂立即扩展。我们标出了38.8s处的P波前沿、超剪切（S－S）马赫锥和次瑞利（S－R）滑动脉冲。在高应力环境下，长度为100km（近似为断层阶跃模型中主、次断层段的总长度）的单个走滑断层模型并未显示出超剪切破裂转换，证明转换并非方向性的结果。

3 讨论

本研究重点研究不同摩擦定律对沿走滑断层阶跃的破裂扩展的影响。采用较为实际的实验室导出的摩擦定律来模拟破裂过程是地震学永恒的追求。速率—状态依从的摩擦公式不仅包括如时间、滑动速度过程和正应力过程等的直观变量，而且展现出如黏滑错动、蠕动、愈合等的合理特性（Dieterich，1978，1979；Linker and Dieterich，1992）。在我们的摩擦框架中，我们采用大约0.6m的有效滑动弱化距离d0来对所有摩擦关系建立统一性。这与近来研究得出的有效滑动弱化距离为1m量级的结果一致（Ide and Takeo，1997；Olsen et al，1997）。我们的研究结果显示，摩擦的函数形式对断层阶跃的破裂动力学过程有显著影响。当假定所有摩擦参数的d0恒定时，我们发现能量收支的差异与最大跨越距离的差异相关联（特别是与总能量释放相关的表面能量）。在这些情况下，速率—状态滑动定律的破裂能量密度比速率—状态衰变定律或滑动弱化定律的小，且产生更多的地震辐射从而使破裂可以跨越更远的距离。当将各个摩擦定律的破裂能量密度设为相等时，最大跨越距离的差异大幅下降，但是滑动定律的较大初始应力—滑移斜率仍使其产生稍大的最大跨越距离。进一步减小差异的一个方法可能是增加采用经典滑动弱化摩擦和衰变定律的模型的初始剪切应力以使它们如滑动定律一样具有相同的平均地震辐射量。当d0相等或破裂能量相等时，不同摩擦公式的最大跨越距离，高应力模型比低应力模型更为相似。这意味着用高绝对应力模拟跨越破裂时摩擦定律的类型可变得不太重要。我们还指出，衰变定律与滑动弱化摩擦相似，产生了近似线性的弱化曲线，使得模拟衰变定律时比模拟滑动定律更容易调整滑动弱化摩擦。然而，速率—状态依从的摩擦一个非常重要的方面，特别是衰变定律，是滑动弱化摩擦不能模拟的直观的愈合过程（例如，摩擦强度随接触时间增加）。因而，尽管滑动弱化和速率－状态衰变定律的断层阶跃短期跨越行为非常相似，但这些不同摩擦假设下的断层长期行为可能非常不同。

我们的研究结果显示，破裂能跨越某一特定断层阶跃的可能性取决所使用的摩擦参数。观察跨越的破裂可使我们进一步了解哪个摩擦定律更有效。例如，对于已知的应力降、跨越距离、断层几何形态和滑动时间分布，人们就可用优选的摩擦定律提供简单的模型。采用的演化定律可影响破裂跨越断层阶跃的可能性，并影响模拟地震的预测震级。这一效应对于小的阶跃宽度可能至关重要，特别是当部分断层经受强速率弱化时。高滑动速率的地震会特别易受非线性弱化曲线和摩擦系数中大动态应力降的影响，进而跨越阶跃的可能性更大。显示这种非线性弱化曲线的高速实验室研究，无疑是探索真实断层的动力学模拟中强速率弱化特性的很好理由。根据我们的一般结果，基于真实断层阶跃的动力学模拟可随所用摩擦定律（以及应力状态和材料属性）的不同而产生不同的结果。我们还看到在高应力状态下，3种不同的摩擦定律（除了强速率弱化滑动定律）的最大跨越距离往往收敛到最大跨越值，表明在高应力降、高地震辐射的均匀模型中考虑不同摩擦定律的影响也许并非决定因素。然而，摩擦定律的影响在哪种环境下更突出并不明显（如非均匀预应力）。

对于高应力状态我们证明，尽管沿断层的初始地震S比率（2.6）太大以至于不能在平面走滑断层上发生转换，但断层阶跃仍可作为之前未被证实的超剪切转换模式的触发因素。来自主断层段的地震波改变了次断层段再起始区域破裂前的应力场，使该区域的地震S比率达到允许发生超剪切破裂速度的值。一旦破裂达到超剪切速度，它甚至可在有利应力区域外保持超剪切。其他数值模拟表明了沿走滑断层的超剪切转换机制，包括高摩擦阻力区域（Dunhamet al，2003）和有利的预应力（Fukuyama and Olsen，2002；Liu and Lapusta，2008）和断层走向变化（Oglesby et al，2008；Oglesby and Mai，2012）区域。对具有摩擦界面的光弹板材料的实验室试验显示了次瑞利到超剪切的转换。然而，它们的初始应力状态允许Burridge－Andrews机制下的超剪切速度。与次瑞利破裂相比，超剪切破裂速度的观测证据表明了很强的平行断层的地面运动（例如，Archuleta，1984；Dunham and Archuleta，2004），而且在我们的超剪切模型中沿S波马赫锥我们也看到了这样的运动。我们发现本研究中的超剪切转换可能是高预应力状态下特有的，因为未在低预应力模型中看到它。此外，我们的研究局限于相对较大的地震事件。由于超剪切转换并未在自然界沿断层阶跃的各种大小地震中大量观测到，它可能需要特定的预应力状态和断层几何形态。约束诸如材料属性、预应力和摩擦状态以及断层几何形态等能导致断层阶跃超剪切破裂转换的变量还需进一步深入的研究。目前的工作为自然界一系列断层属性中那些可能提供了指示，但也许没有什么是最有可能。

我们承认本研究存在一些局限性，因此未来的研究可在现有结果上进行扩展。所有模型都是二维的，表明破裂能量集中在平面上，因此产生了比类似的三维模型更大的平均滑动、滑动速率和应力降。本研究产生的模型主要是裂纹型的（即，滑动脉冲为空间上大且渐近下降），可能是大载荷应力（初始剪应力）的原因（Zheng and Rice，1998）。尽管实验推导是在低滑动速率，但我们采用了空间均匀的摩擦属性并假定速率—状态依从的摩擦以高滑动速率进行，表明我们的模型并未完全考虑大尺度的凹凸体和滑移速率。此外，次断层的应力状态被停止相（由主断层的破裂快速终止产生的地震辐射，它可使破裂在次断层段上再次起始）所改变（Madariaga，1976）。我们模型中的停止相由于各断层段端部以高摩擦系数嵌于一个单元而产生。Oglesby（2008）研究显示，滑移梯度和破裂加速度可通过调整停止相振幅而强烈地影响最大跨越距离。尤其是，随着主断层边缘处应力和滑移梯度的下降，破裂跨越的能力也随之降低。然而，在断层阶跃中都观察到高滑动和低滑动两种梯度（Elliot et al，2009）。未来的研究将结合与正应力相关的状态变量，以产生更符合实际的破裂（Linker and Dieterich，1992）。在速率—状态依从的框架内包含与正应力相关的状态变量可以突出或削弱压性与张性阶跃间的正应力不对称。这一摩擦参数可能会改变正应力扰动较大区域的能量收支。

另外，我们模拟的断层几何形态是对真实不相连断层阶跃的简化，断层段很可能被具有走向和滑动方向略有不同的小断层和裂纹的区域所分离。对于为模拟地震大小和地面运动估计的特定地质特征而设计的模拟工作，研究断层阶跃更实际更复杂断层结构的影响可能是至关重要的。例如，Lozos等（2012）研究了断层阶跃小的中间断层对破裂扩展的影响，发现它们的存在是促进还是阻碍破裂扩展依赖于几何细节和断层段的滑动方向。然而，目前研究的重点是约束不同摩擦参数的影响，因此，我们限制了那些可能由复杂断层几何形态引起的复杂情况以避免额外的困难。与断层阶跃的经典研究（例如，Harris and Day，1993）的对比，同样借助了简化的断层几何模型。然而，在本研究框架下，研究两个断层段之间及其周边区域从能量损耗到非弹性运动的影响是有意义的。Andrews（2005）研究表明，损伤区域（远离主滑动面）的能量损耗使破裂能量随着破裂扩展而增加。相对于无损伤区域的主滑移面的破裂，这一效应反过来降低了破裂扩展速度。在本研究中将非弹性能量损耗考虑进去可影响停止相的强度及它们对跨越破裂的影响，必定会改变断层阶跃区及周边区域的能量收支。Andrews（2005）进一步指出，人为限制动态破裂速度是模拟非弹性响应的一种方法。

Andrews，D.J.（1976），Rupture velocity of plane strain shear cracks，J.Geophys.Res.，81，5679－5687，doi：10.1029／JB081i032p05679.

Andrews，D.J.（1985），Dynamic plane－strain shear rupture with a slip－weakening friction law calculated by a boundary integral method，Bull.Seismol.Soc.Am.，75（1），1－21.

Andrews，D.J.（2005），Rupture dynamics with energy loss outside the slip zone，J.Geophys.Res.，110，B01307，doi：10.1029／2004JB003191.

Archuleta，R.J.（1984），A faulting model for the 1979Imperial Valley earthquake，J.Geophys.Res.，89，4559－4585，doi：10.1029／JB089iB06 p04559.

Barall，M.（2008），FaultMod finite element code.［A－vailable at http：／／scecdata.usc.edu／cvws／download／codedesc／Barall＿FaultMod＿Desc.pdf.］

Barall，M.（2009），A grid－doubling finite－element technique for calculating dynamic three－dimensional spontaneous rupture on an earthquake fault，Geophys.J.Int.，178，845－859.

Bartlett，W.L.，M.Friedman，and J.M.Logan（1981），Experimental folding and faulting of rocks under confining pressure，Tectonophysics，79，255－277.

Beeler，N.M.，and T.E.Tullis（2003），Constitutive relationships for fault strength due to flashheating，Southern California Earthquake Center Annual Meeting Proceedings and Abstracts，Los Angeles，Calif.

Beeler，N.M.，T.E.Tullis，and D.L.Goldsby 2008Constitutive relationships and physical basis of fault strength due to flash heating，J.Geophys.Res.， 113， B01401， doi：10.1029／2007JB004988.

Bernard，P.，and D.Baumont（2005），Shear Mach wave characterization for kinematic fault rupture models with constant supershear rupture velocity，Geophys.J.Int.，162，431－447.

Bernard，P.，and R.Madariaga（1984），High－frequency seismic radiation from a buried circular fault，Geophys.J.R.Astron.Soc.，78，1－17.

Bizzarri，A.，and M.Cocco（2003），Slip－weakening behavior during the propagation of dynamic ruptures obeying rate－and state－dependent friction laws，J.Geophys.Res.，108（B8），2373，doi：10.1029／2002JB002198.

Bizzarri，A.，M.Cocco，D.J.Andrews，and E.Boschi（2001），Solving the dynamic rupture problem with different numerical approaches and constitutive laws，Geophys.J.Int.，144，656－678.

Bouchon，M.，and M.Vallée（2003），Observation of long supershear rupture during the magnitude 8.1Kunlunshan earthquake，Science，301，824－826.Burridge，R.（1973），Admissible speeds for planestrain self－similar shear cracks with friction but lacking cohesion，Geophys.J.R.Astron.Soc.，35，439－455.

Cocco，M.，and A.Bizzarri（2002），On the slip－weakening behavior of rate－and state－dependent constitutive laws，Geophys.Res.Lett.，29 （11），1516doi：10.1029／2001GL013999.

Cochard，A.，and J.R.Rice（2000），Fault rupture between dissimilar materials：Ill－posedness，regularization，and slip－pulse response，J.Geophys.Res.，105 （B11），25，891－25，907，doi：10.1029／2000JB900230.

Dalguer，L.A.，and S.M.Day（2007），Staggered－grid split－node method for spontaneous rupture simulation，J.Geophys.Res.，112，B02302，doi：10.1029／2006JB004467.

Das，S.，and K.Aki（1977），Fault plane with barriers：A versatile earthquake model，J.Geophys.Res.，82（36），5658－5670，doi：10.1029／JB082 i036p05658.

Day，S.M.（1982），Three－dimensional Simulation of Spontaneous Rupture：The effect of nonuniform prestress，Bull.Seismol.Soc.Am.，72，1881－1902.

Dieterich，J.H.（1978），Time－dependent friction and the mechanics of stick－slip，Pure Appl.Geophys.，116，790－806.

Dieterich，J.H.（1979），Modeling of rock friction 1.Experimental results and constitutive equations，J.Geophys.Res.，84（B5），2161－2168，doi：10.1029／JB084iB05p02161.

Dieterich，J.H.，and B.D.Kilgore（1994），Direct observation of frictional contacts：New insights for state－dependent properties，PAGEOPH，143，283－302.

Duan，B.，and D.D.Oglesby（2006），Heterogeneous fault stresses from previous earthquakes and the effect on dynamics of parallel strike－slip faults，J.Geophys.Res.，111，B05309，doi：10.1029／2005JB004138.

Dunham，E.M.（2007），Conditions governing the occurrence of supershear ruptures under slipweakening friction，J.Geophys.Res.，112，B07302，doi：10.1029／2006JB004717.

Dunham，E.M.，and R.J.Archuleta（2004），Evidence for a supershear transient during the 2002Denali Fault earthquake，Bull.Seismol.Soc.Am.，94，S256－S268.

Dunham，E.M.，P.Favreau，and J.M.Carlson（2003），A supershear transition mechanism for cracks，Science，299，1557－1559.

Elliot，A.J.，J.F.Dolan，and D.D.Oglesby（2009），Evidence from coseismic slip gradients for dynamic control on rupture propagation and arrest through stepovers，J.Geophys.Res.，114，B02312，doi：10.1029／2008JB005969.

Ellsworth，W.L.，M.Celebi，J.R.Evans，E.G.Jensen，R.Kayen，M.C.Metz，D.J.Nyman，J.W.Roddick，P.Spudich，and C.D.Stephens（2004），Near－field ground motion of the 2002Denali Fault，Alaska，earthquake recorded at pump station 10，Earthquake Spectra，20，597－615.

FukuyamaE.and K.B.Olsen2002A condition for super－shear rupture propagation in a heterogeneous stress field，Pure Appl.Geophys.，159，2047－2056.

Goldsby，D.L.，and T.E.Tullis（2002），Low frictional strength of quartz rocks at subseismic slip rates，Geophys.Res.Lett.，29（17），1844，doi：10.1029／2002GL015240.

Harris，R.A.，and S.M.Day（1993），Dynamics of fault interaction：Parallel strike－slip faults，J.Geophys.Res.，98 （B3），4461－4472，doi：10.1029／92JB02272.

Harris，R.A.，and S.M.Day（1997），Effects of a low－velocity zone on a dynamic rupture，Bull.Seismol.Soc.Am.，87，1267－1280.

Harris，R.A.，and S.M.Day（1999），Dynamic 3D simulations of earthquakes on en echelon faults，Geophys.Res.Lett.，26 （14），2089－2092，doi：10.1029／1999GL900377.

Harris，R.A.，R.J.Archuleta，and S.M.Day（1991），Fault steps and the dynamic rupture process：2－D numerical simulations of a spontaneously propagating shear fracture，Geophys.Res.Lett.，18（5），893－896，doi：10.1029／91GL 01061.

Harris，R.A.，et al.（2009），The SCEC／USGS dynamic earthquake rupture code verification exercise，Seismol.Res.Lett.，80，119－126.

Hirose，T.，and T.Shimamoto（2005），Growth of the molten zone as a mechanism of slip weakening of simulated faults in gabbro during frictional melting，J.Geophys.Res.，110B05202，doi：10.1029／2004JB003207.

Ida，Y.（1972），Cohesive force across the tip of a longitudinal－shear crack and Griffith's specific surface energy，J.Geophys.Res.，77（20），3796－3805，doi：10.1029／JB077i020p03796.

Ide，S.，and M.Takeo（1997），Determination of constitutive relations of fault slip based on seismic wave analysis，J.Geophys.Res.，102（B12），27，379－27，391，doi：10.1029／97JB02675.

Kanamori，H.，and L.Rivera（2006），Energy Partitioning During an Earthquake，Earthquakes：Radiated Energy and the Physics of Faulting.Geophys.Monogr.Ser.，vol.170，AGU，Washington，D.C.，doi：10.1029／170GM03.

Kase，Y.，and K.Kuge（1998），Numerical simulation of spontaneous rupture processes on two noncoplanar faults：The effect of geometry on fault interaction，Geophys.J.Int.，135，911－922.

Knuepfer，P.L.K.（1989），Implications of the characteristics of endpoints of historical surface fault ruptures for the nature of fault segmentation，U.S.Geol.Surv.Open－file Rep.，193－228.

Lettis，W.，J.Bachhuber，R.Witter，C.Brankman，C.E.Randolph，A.Barka，W.D.Page，and A.Kaya（2002），Influence of releasing step－overs on surface fault rupture and fault segmentation：Examples from the 17August 1999Izmit earthquake on the North Anatolian Fault，Turkey，Bull.Seismol.Soc.Am.，92，19－42.

Linker，M.F.，and J.H.Dieterich（1992），Effects of variable normal stress on rock friction：Observations and constitutive equations，J.Geophys.Res.，97 （B4），4923－4940，doi：10.1029／92JB00017.

Liu，Y.，and N.Lapusta（2008），Transition of mode II cracks from sub－Rayleigh to intersonic speeds in the presence of favorable heterogeneity，J.Mech.Phys.Solids，56，25－50.

Lozos，J.C.，D.D.Oglesby，J.N.Brune，and K.B.Olsen（2012），Small intermediate fault segments can either aid or hinder rupture propagation at stepovers，Geophys.Res.Lett.，39L18305，doi：10.1029／2012GL053005.

Madariaga，R.（1976），Dynamics of an expanding circular fault，Bull.Seismol.Soc.Am.，66，639－666.

Madariaga，R.，and K.B.Olsen（2000），Criticality of rupture dynamics in 3－D，Pure Appl.Geophys.，157，1981－2001.

Mai，P.M.，P.Somerville，A.Pitarka，L.Dalguer，S.Song，G.Beroza，H.Miyake，and K.Irikura（2006），On scaling of fracture energy and stres drop in Dynamic Rupture Models：Consequences for Near－Source Ground Motions，Earth－quakesRadiated Energy and the Physics of Faulting，Geophys.Monogr.Ser.，vol.170，pp.283－293，AGU，Washington，D.C.

Manighetti，I.，M.Campillo，S.Bouley，and F.Cotton（2007），Earthquake scaling，fault segmentation，and structural maturity，Earth Planet.Sci.Lett.，253，429－438.

Nielsen，S.B.，and K.B.Olsen（2000），Constraints on stress and friction from dynamic rupture models of the 1994Northridge，California，Earthquake，Pure Appl.Geophys.，157，2029－2046.

Oglesby，D.D.（2008），Rupture termination and jump on parallel offset faults，Bull.Seismol.Soc.Am.，98，440－447.

Oglesby，D.D.，and P.M.Mai（2012），Fault geometry，rupture dynamics and ground motion from potential earthquakes on the North Anatolian Fault under the Sea of Marmara，Geophys.J.Int.，188，1071－1087.

Oglesby，D.D.，P.M.Mai，K.Atakan，and S.Pucci（2008），Dynamic models of earthquakes on the North Anatolian fault zone under the Sea of Marmara：Effect of hypocenter location，Geophys.Res.Lett.，35，L18302，doi：10.1029／2008 GL035037.

Okubo，P.G.（1989），Dynamic rupture modeling with laboratory－derived constitutive relations，J.Geophys.Res.，94（B9），12，321－12，335，doi：10.1029／JB094iB09p12321.

Olsen，K.B.，R.Madariaga，and R.J.Archuleta（1997），Three－dimensional dynamic simulation of the 1992Landers earthquake，Science，278，834－838.

Olson，A.H.，and R.J.Apsel（1982），Finite faults and inverse theory with applications to the 1979 Imperial Valley earthquake，Bull.Seismol.Soc.Am.，72，1969－2001.

Palmer，A.C.，and J.R.Rice（1973），The growth of slip surfaces in the progressive failure of overconsolidated clay，Proc.R.Soc.London，Ser.A，332，527－548.

Prakash，V.（1998），Frictional response of sliding in－terfaces subjected to time varying normal pressures，J.Tribol.，120，97－102.

Prakash，V.，and F.Yuan（2004），Results of a pilot study to investigate the feasibility of using new experimental techniques to measure sliding resistance at seismic slip rates，Abstract JHJT21D－02presented at 2004Fall Meeting，AGU.

Rabinowicz，E.（1951），The nature of the static and kinetic coefficients of friction，J.Appl.Phys.，22，1373－1379.

Rice，J.R.（1999），Flash heating at asperity contacts and rate－dependent friction，Eos Trans.AGU，77，Fall Meet.Suppl.，Abstract F6811.

Rice，J.R.（2006），Heating and weakening of faults during earthquake slip，J.Geophys.Res.，111，B05311，doi：10.1029／2005JB004006.

Rojas，O.，E.M.Dunham，S.M.Day，L.A.Dalguer，and J.E.Castillo（2009），Finite difference modeling of rupture propagation with strong velocity－weakening friction，Geophys.J.Int.，doi：10.1111／j.1365－246X.2009.04387.x.

Rosakis，A.J.（2002），Intersonic shear cracks and fault ruptures，Adv.Phys.，51，1189－1257.

Rosakis，A.J.，O.Samudrala，and D.Coker（1999），Cracks faster than the shear wave speed，Science，284，1337－1340.

Ruina，A.（1980），Friction laws and instabilities：A quasistatic analysis of some dry friction behavior，PhD thesis，Dep.Of Mech.Eng.，Brown Univ.，Providence，R.I.

Ruina，A.（1983），Slip instability and state variable friction laws，J.Geophys.Res.，88（B12），10，359－10，370，doi：10.1029／JB088iB12p10359.

Scholz，C.H.，C.A.Aviles，and S.G.Wesnousky（1986），Scaling differences between large interplate and intraplate earthquakes，Bull.Seismol.Soc.Am.，76，65－70.

Segall，P.，and D.D.Pollard（1980），Mechanics of discontinuous faults，J.Geophys.Res.，85（B8），4337－4350，doi：10.1029／JB085iB08p04337.

Sibson，R.H.（1973），Interactions between temperature and pore－fluid pressure during earthquake faulting and a mechanism for partial or total stress reliefNat.Phys.Sci.24366－68.

Sieh，K.，et al.（1993），Near－field investigations of the Landers earthquake sequence，April to July 1992，Sci.New Ser.，260，171－176.

Spudich，P.，and E.Cranswick（1984），Direct observation of rupture propagation during the 1979 Imperial Valley earthquake using a short baseline accelerometer array，Bull.Seismol.Soc.Am.，74，2083－2114.

Spudich，P.，and L.N.Frazer（1984），Use ray theory to calculate high－frequency radiation from earthquake sources having spatially variable rupture velocity and stress drop，Bull.Seismol.Soc.Am.，74，2061－2082.

Tsutsumi，A.，and T.Shimamoto（1997），High－velocity frictional properties of gabbro，Geophys.Res.Lett.，24（6），699－702，doi：10.1029／97 GL00503.

Tullis，T.E.，and D.L.Goldsby（2003a），Laboratory experiments on fault shear resistance relevant to coseismic earthquake slip，Southern California Earthquake Center Annual Progress Report，Los Angeles，Calif.

Tullis，T.E.，and D.L.Goldsby（2003b），Flash melting of crustal rocks at almost seismic slip rates，Abstract JHJS51B－05presented at 2003 Fall Meeting，AGU.

Vedder，J.G.，and R.E.Wallace（1970），Map showing recently active breaks along the San Andreas and related faults between Cholame Valley and Tejon Pass，California，U.S.Geol.Surv.Misc.Field Invest.Map，I－574，scale 1：24000.

Wesnousky，S.G.（1988），Seismological and structural evolution of strike－slip faults，Nature，335，340－343.

Wesnousky，S.G.（2006），Predicting the endpoints of earthquake ruptures，Nature，444，358－360.

Xia，K.，A.J.Rosakis，and H.Kanamori（2004），Laboratory earthquakes：The sub－Rayleigh－to－supershear rupture transition，Science，303，1859－1861.

Xia，K.，A.J.Rosakis，H.Kanamori，and J.R.Rice（2005），Laboratory earthquakes along inhomo－geneous faultsDirectionality and supershear Science，308，681－684.

Zheng，G.，and J.R.Rice（1998），Conditions under which velocity－weakening friction allows a selfhealing versus a cracklike mode of rupture，Bull.Seismol.Soc.Am.，88，1466－1483.