初等数论在历史年代学中的应用

罗见今

（内蒙古师范大学科学技术史研究院，呼和浩特010022）

初等数论在历史年代学中的应用

罗见今

（内蒙古师范大学科学技术史研究院，呼和浩特010022）

应用初等数论中的同余式、连分数、渐近分数、不定方程等工具，分析考古年代学提出的若干问题，以敦煌汉简、居延汉简、《史记》等出土文物和史料为证据，将《二十史朔闰表》、《三千五百年历日天象》的记录视为大时段日月运行的数据库，证明或论述中国历法的五个周期性质，从而阐明应用数学进行年代考释的基本原理和方法。

初等数论；汉代简牍；朔闰表；历法的周期性质；考古年代学

一、研究的背景和问题的提出

当人们研究一个历史问题或遇到一件出土文物的时候，首先须回答：它是什么朝代、什么时期的？有时还须进而了解：它是哪一年、哪一月的？这就是史学中的断代问题，在整个历史科学、特别是考古学中占有重要的地位。历史、考古、文物工作者在长期的实践和研究工作中具有丰富的经验，形成了年代学的基本理论，对大量年代学实际问题作出了科学而准确的判断。人们现在所知关于历史上的一切，几乎都建立在年代学的框架之中。这个基本框架经历了千千万万史实的验证，是不可动摇的。

然而人们也不能忘记，史学家们所面对的是五千年悠久的历史。由于自然和人的作用，关于古代纪年的信息所存无几；随着时间的流逝，“过去”离我们愈加遥远、变得模糊不清。大量的问题不是“拂去尘封”就可以探知其真的。历史是复杂的，它充满了矛盾。人们有理由怀疑史书中个别年月日的记录，因它是否后来所修，或有改写的动机；也可以指谪历谱中的错误，认为它主要靠推算而得，不见得是当时的应用历谱；或者把希望寄托在出土的文物之上：它的年号、月朔记录应当是真实的。然而，出土文物的记录也可能出现牴牾，例如：1930年在今内蒙古西部出土的“居延汉简”中有一枝（编号137·3，224·18）为：［1］

建平五年（前2）十二月丙寅朔乙亥诚北候长□充□言之官下诒诣（符号“□”表示原来木简上的字难以辨认，“”表示以下部分断缺。下略）。

但是另有一枝（编号495·12A，506·20A）却是：［2］

两简同是同年十二月，但朔日（初一日）的干支却相差25天！究竟哪一枝记录可信呢？如果查一查史学界通用的、陈垣先生编《二十史朔闰表》，［3］得知建平五年（即元寿元年）十二月乙未朔，与两简所记又不相同！如果你继续去查宋人刘羲叟的《长历》、清人汪曰桢的《历代长木辑要》［4］以及《汉书》［5］（第3册848页记，该年十二月有庚子日），你会得出互相矛盾的结论而莫知所从。

当然，这个例子较典型但并不普遍。由于分治、战乱、改历等因素的影响，有些历史阶段会出现各地使用历谱不完全一致的情况；而竹木简的记载也可能有笔误、释文错误等问题。绝大多数历史记载、历谱、文物的时间记录基本是真实的，但又不是绝对正确的，需要进行具体的分析。

另一方面，史学家对同一历史事件年代的判断可以出现重大分歧。最著名的一例是武王伐纣之年代，从西汉末的刘歆开始，到1997年为止，至少发表了106种论著，提出了多达44种不同的伐纣之年，其上下限为前1130年到前1018年。［6］如果史学家都争论不已，一般人更是莫所适从了。所以国家拨巨款，从事“断代工程”的年代学研究，以确定夏、商、周的年代。其成果当然对于中国历史具有重要意义。

事实上，除了这类重大的课题之外，应用传统的史学方法对于判定某些文物的年代、推算某些年代的历谱等也可能出现错误。虽然无关重大历史事件，但有悖于历史的真实，也应当予以纠正。在下文中将举出具体例子说明。更多的情况是传统的方法无法对文物精确断代，只好划出一个大致的时代上下限，使之处于模糊的状态。

随着现代科学技术的进步，天文、数学、物理、化学等方法开始在年代学领域中取得巨大成果，成为断代的有力工具。用天文学方法进行考古卓有成效，备受中外科学家的重视，已形成了“考古天文学”的分支。利用测定文物放射性的方法确定年代日臻完善，例如1947年利比创放射性同位素C14法测定年代已被大量使用。还有利用红外线、电脑图象识别等方法。其中，根据历史、考古知识，利用历法、数学方法，建立合适的数学模型，推导出一系列周期定理和判定定理，用来做考证年代的工具，简便、适用、精确，与传统方法结合紧密，值得系统讨论。

众所周知，中国传统历法又称为“干支历”。相传黄帝之臣大挠创甲子，乙丑，……癸亥，干支相配纪日、六十周而复始，是我国先人的伟大创造，其意义可与数字的发明相媲美。学术界一般认为传统历法自鲁隐公元年（前722）以来，干支纪日至今未间断，将近一百万天的连续记录，在世界历法史上绝无仅有，并相信这一天的到来，更多的人们会体会到它的价值。我们把干支纪日的既不重复、又不间断的性质称为“连续原理”，它是进行一切历法、数学的计算、推理的基础。

干支纪日具有独特之处。现有一例：20世纪初出土的“敦煌汉简”中有一枝历谱简（编号97），背面记有“闰（十二）月丙申朔大”［7］。因它是散简，并不知是哪一年的。根据简正面十二个月朔的记载，确认此闰月应是闰十二月；经考证知此历谱简属西汉宣帝神爵三年（前59）。考证有许多根据；但是，仅根据“闰（十二）月丙申朔大”这一信息，就可以完全确定它为神爵三年简，因为它是非常独特的：在从公元前206年西汉始，至2000年的两千二百多年中，仅有公元前59年是“闰十二月丙申朔大”。这种唯一性受到闰十二月周期性、丙申朔的周期性、大月的周期性的限定，往往被人忽视。同样，大量无年号的朔闰干支记录也都包含着各自的周期性和独特性秘密，期待着人们去破解。相比之下，西历如果记有“12月1日”，它可能属于两千多年中的任意一年，对于断代则无所助益。由此凸显出干支历的特殊性，对于考释年代，不啻为解决问题的一把钥匙。

中国历法原被称为“皇历”，因制历权为朝廷特有，并以皇帝名义颁行天下；后来又叫“农历”。在民间流行称为“阴历”（月亮历），其实是不对的，应是阴阳合历（月亮—太阳历），因它既含月象盈亏，又合寒暑时令。它的一年有354日（也有355日），闰年384日（也有383、385日）；它的一个月大月有30日，小月29日。但实际上1回归年有365.242 198 78日，而1朔望月有29.530 588 67日。中国历代天文历法家经过千百年持续不断的努力，精确地观测天象，编制优秀的历法，使之与日月星辰的运行尽量相合。几千年过去了，中国历法作为一个整体，平均每年的日数、平均每月的日数分别与回归年、朔望月逐渐相合，本文称其为“趋同原理”。历法中的许多周期性质是由日、月的周期，干支周期共同决定的，它们建立在趋同原理的基础之上。

二、应用初等数论的方法解决历法问题

为研究干支的周期性，须了解初等数论中的同余理论。对于整数a，b及正整数m有下列关系：

a=mq1+r1（0≤r1≤m），b=mq2+r2，（0≤r2≤m）

而r1=r2；则说：a，b对于模数的m为同余，也可以说：对于模数m，a，b同余，记作a≡b(mod m)上式叫做同余式。例如，42、50被8除，得到的余数都是2，于是说：42、50对于模数8为同余，记作42≡50（mod 8）；又如-11、16被3除，得到的余数都是1，于是说-11、16对于模数3同余，记作-11≡16（mod 3）。由定义可证明a-b可被m整除。

同余有诸多性质，包含深刻的内容。用它研究干支，可以得到一些计数的结果。为此，先将甲子，乙丑，……，癸亥依次用01，02，…，60表示，记作A（或B，N等）每个A都由天干a（a=1，2，…，10）和地支b（b=1，2，…，12）构成，于是有

A=a（mod 10），A=b（mod 12），A=6a-5b（mod 60）

如果从干支A（a1,b1）计数到B（a2,b2），得到N（≤60），那么N表示两干支之间的距离，有

任意两干支日之间有多少天？这是一个复杂的问题，计算往往出错。但实际问题非常之多。例如：

建武六年七月戊戌朔乙卯甲渠障候敢言府书曰吏民毋得伐树木……（EPT22.53A）［8］

要问：乙卯是几号？这是公元30年7月1日戊戌（5，11）到乙卯（2，4）日，上式表明可用两种方法计算：乙卯B=52，戊戌A=35，据式可求出N=18；在不记得A，B的干支序号时，据式亦可求出N=18。

通常这种求日期算法均用历谱或60干支表，一个个口数心计；列出算式可制程序交给计算机去完成的。

干支纪日具有顺序意义、循环意义、数字意义。60甲子周期同回归年和朔望月的日数（可以看作是无理数）不可公度，也就是不能找出三者之间都恰好合适的公倍数。在初等数论中便借助于连分数、渐近分数的方法来解决。

这种方法可以继续进行下去，得到一个层层迭迭的分数，叫做连分数。任何一个实数都可以表示成连分数的形式。上例用一种简单的写法可记作x=［1，1，1，1，…］。

应用迭代法，将试值x=1代入原式，得出x=1/2；将它再代入原式右边，得出x=2/3；循此继进，可求出一系列分数：这同将试值x=1代入连分数的第1，2，…各层后展开的结果是相同的。其实，原式本来就是方程，求出的一个根是，即黄金分割，x=0.618 033 988 7。上列分数值逐渐向这个极限靠近，所以把它称为渐近分数。

我国西汉时已知求连分数，计算历法问题卓有成效。以下引用华罗庚［9］先生的一个例子：怎样算农历的闰月？将回归年和朔望月的日数相除：

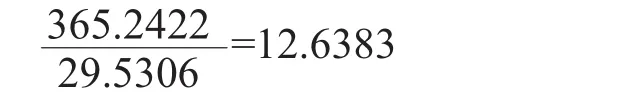
说明一年应有12个朔望月，另外还余0.3683个月。应用辗转相除法将它展开成连分数，得

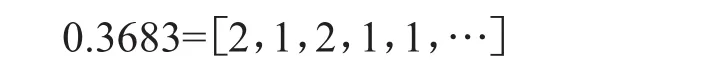
它的渐近分数为（用更精确的数据获得）

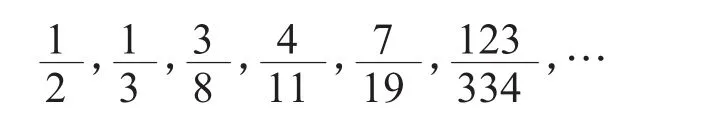
这表明：两年一闰太多，三年一闰太少；八年三闰较多，十一年四闰较少；十九年七闰较多，334年123闰略少……古人常用十九年七闰；，积17个7闰之后，在下个11年中只作4闰，就更合于日、月的运行。以上对初等数论的同余和连分数作了简介，对于了解以下内容是必要的。

三、两列渐近分数

我国古代天文历法可分为观象授时时期（上古至春秋中）、历法准备时期（春秋中至战国中）、历法制定时期（战国中至汉太初元年）。到《三统历》臻于完备，载于《汉书·律历志》。简言之，汉代以来历法、史书、文物的证据较先秦为多，在年代学中应用数字方法可以找到历史记录作为证据。

几千年来中国传统历法是一个整体、一个系统，虽然各个时期、每种历法都有它的特点，但可作为分段演绎系统来考察。因此，有必要将陈垣《二十史朔闰表》等看作一个数据库、把它作为数字研究的对象，认为历谱中的记录包含了日月运行的周期性、干支纪日的周期性等多方面的信息。本文将应用天文年历中精确的回归年和朔望月数值，并以出土文物（主要是简牍中的纪年）和《史记》、《汉书》等史书中的有关记载作为根据。

今记回归年α=365.24219878，朔望月β=29. 53058867，设γ=α/β－12=0.36826678。问题是，若经过S年使得每年所余γ月尽可能的凑足整月数t，即Sγ≈t，则称t为闰月数（也就是闰年数）。即在S年内应有t个闰年。γ≈t/S，可将γ写成连分数，再展开为渐近分数ti/Si。承上，利用精确的α，β值，所得结果为：

将这些理论计算的数值与朔闰表的实际结果相对照，人们会吃惊地发现，两者几乎完全吻合！翻开陈垣《二十史朔闰表》，任取相差1021年或1708年的两年，其间的闰年数恰为376年或629年！如果不合，往往是由于数错造成。对于上列渐近分数中的最后一个，问题在于2729年中是否真的有1005闰？须查张培瑜的《三千五百年历日天象》［10］，如果从公元前721年（鲁隐公元年）起算，1995年是第一个“千闰年”，2009年将迎来第1005闰，也可以看作是第六个千闰年。这充分说明我国历代的天文历法学家，以他们坚持不懈的共同努力，使历法的精度渐次密合于天象；千闰年的出现，是趋同原理的典型事件，具有深刻的天文—历法意义和丰富的数学内涵。［11］

当然，不同历法如何置闰可以小有区别，但目的都是使所制定的历法与太阳运行相调，称为调日法。同时，不同历法又必须安排好大小月的顺序和两者间的数量比，以使历法与月亮圆缺相谐，这里称为谐月法。因β-29.5=0.03058867，说明大月的总数应当比小月多，设一个阶段（比如q年）中大月数减小月数的差为谐月数φ（整数），那么谐月法就是要解决在q年中应加入多少个谐月的问题。

设m=30日为1谐月（它是1大月，也可能是蝉联大月的后一个月），n=29.5日为1平月（大小月均值），ε=β－n=0.03058867日为1平月不足1朔望月之日数，δ=m－β=0.46941133日为1谐月多于1朔望月之日数。显然ε+δ=m－n=0.5。设比值μ为每过qi年应增添的pi个谐（大）月，可以证明（此略）：

表示成渐近分数，即有

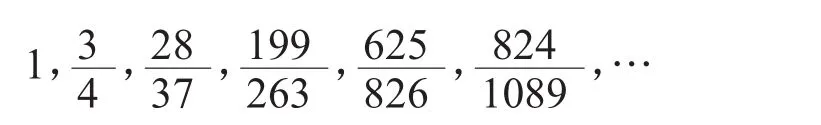
μ的意义不太直观，最后一个分数表示1089年中应有824个谐月，从月朔表中我们同样获得了有力的证据（关键是按定义计算谐月数要准确）。应用这列分数，可求出任一时段q内谐大月数p，q大则精确。以《三统历》（前104到公元85）行用的189年为例。从上列分数中选出28/37和3/4，存在以下等式表明在5个37年中增添5次28个谐大月之后，所余4年应加入3个谐月（此时与的相对误差约十万分之六）。因此p=143对q=189是最佳的选择。而《三统历》的实际情况p值偏小，我们统计（从公元前104年的正月起算）为142谐月。这样，就可以从一个方面对历法精度作出估计。

类似地，可将此法应用到历法研究的更多方面，还可用以分析木星（岁星）、金、火、水、土五星的运行，对于深入认识天文历法，不失为一种有效的工具。历法中常见的周期性质也可以用连分数、渐近分数的方法来证明。

人们有理由关注历谱中不同性质的干支出现的周期性，这些问题有：1.任一朔干支重现周期，2.任一月朔干支重现周期，3.任一闰月朔重现周期，4.某一年朔序（定义见下）重现周期，5.任一八节（定义见下）干支重现周期，等。以往的研究已经提到“农历的年、月也有周期性。……把日干支的周期和农历年月联系起来看，却找不到一个整数的公共周期。我们从实践中，找到了大体上五年和三十一年的两个周期。”［13］这个结论不够清晰、准确，也需要进行论证，但它指出了周期性的存在。

以下列出上述五个周期的性质定理，有的给出简要论证，有的列举它在考古年代学中的应用。

四、干支历特有的与月朔、闰月朔相关的三个周期性质

性质一、任一朔干支会在61、63或65个月后重现。

设A为某月朔干支，在经历了p个大月和q个小月后重现（p，q＞0）。30p+29q一定能被60整除，即p，q的最小值应当满足同余式30p≡-29q（mod 60）因29为素数，必有q=30；此时p为奇数，且q≠2k·30（k=1，2，…），故只取q=30。因大月数p＞q，故可取p=31，33，35，…由历法知在连续60多个月中如果小月仅有30个，则大月不会有37个。否则误差就太大了。故p=31，33，35。由此性质一得证。

31×30+30×29=1800日=30甲子周；33× 30+30×29=1860日=31甲子；35×30+30× 29=1920日=32甲子。

例如：公元前105年12月甲午朔历61个月后到前100年12月甲午朔共经1800日；从1991年正月丙辰朔到1995年12月丙辰朔共历61个月。常见的是中间经过63或65个月。上文所说“大体上五年”的周期应被性质一取代，它是进一步推理的基础。

性质二、任一同月同朔干支可能在26、31或36年后重现。可简记为31n或31n±5年（n=1，2，…）。

设a年u月（这里暂不考虑闰月）w朔，经s年后为b年u月w朔，求最小s之值。显然s=b－a为正整数。如果s年中含d个月，则据性质一，当x, y,z为非负整数时，应有65x+63y+61z=d；另一方面，设s年中闰t个月，则共有的月数d=12s+t，同时满足d=平月数+谐月数。可将不定方程简化，利用历法中的条件淘汰不合用的解（过程较繁，从略），得出三个d值：

d1=321月=12×26+9闰=300平月+21谐月=9480日=158甲子周

d2=384月=12×31+12闰=360平月+24谐月=11340日=189甲子周

d3=445月=12×36+13闰=420平月+25谐月=13140日=219甲子周

统观几千年历谱s1=26年和s3=36年很少出现。例如汉宣帝神爵二年（前60）正月丁未朔，经26年后到汉元帝建昭五年（前34）正月丁未朔；又如汉章帝建初五年（80）正月辛亥朔，经36年到汉安帝元初三年（116）正月辛亥朔等。较多出现的是31n年（n=1，2，…）的周期，对31年=384月而言，实际上由一组解确定，由性质一来看，由4次65个月、1次63个月和1次61个月堆叠而成；这31年同时满足闰12次、包含24个谐大月，用前文所述两列渐近分数可解释为：

性质二对于考证年代十分有用。在许多出土文物例如简牍中，大部分未记年号，有一类仅记有月份和该月朔干支（或其月朔干支可以推算出来），叫做“月朔简”［14］，例如居延汉简“六月癸巳朔”（148.37号），“五月廿八日戊戌”等，它们的年代大部分可以准确推出［15］。这是因为对居延发掘地各探方伴出纪年简上下时限进行统计，其平均值约为18年；而性质二能够保证在31年（2，36年）内同月同朔纪录只有一个，这对考古工作实在太有用了，结合出土信息和简上内容。所定年代能经得起多种考验。在敦煌发掘地的情况也类似。事实上性质二对干支历都是适用的，因此对各历史时期的文物年代鉴定能发挥它的作用。

性质三、闰月同朔干支经常在51、52或57年后重现。

设A年闰u月w朔，经s年后为B年闰v月w朔，求常见的最小s之值。如果s年中含d个月，则据性质一，当x，y，z为非负整数时，应有65x+ 63y+61z=d另外，设s年中闰t个月，则共有的月数d=12s+t－u+v，同时满足d=平月数+谐月数。

这些都是必要条件。闰月朔的条件较复杂，用演绎的方法去求s会遇到很大困难，所以可用归纳的方法，对朔闰表中作为闰月朔的60干支分别进行统计。我们选取从公元前206年（西汉高祖元年）到公元815年（唐宪宗十年）共1021年，其间恰有376闰（与前列渐近分数376/1021相合，说明满足趋同原理）。性质三是统计的结果，它满足已列出的必要条件，讨论如下。

d1=638月，表现为51或52年。在不定方程中x=7，y=0，z=3。51或52年中必有19闰，因

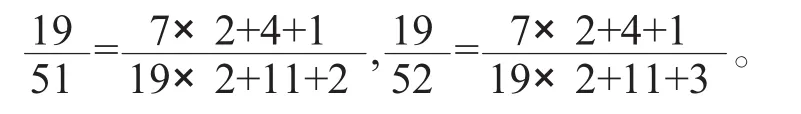
故对51年，d1=638=51×12+19－u+v，即vu=7。说明凡过51年出现同朔之闰月，相差月数为7。对52年，d2=638=52×12+19－u+v，即v－u=5。说明凡过52年出现同朔之闰月，相差月数为5。

在51或52年中应有38个谐月，这时d1=638月=600平月+38谐月=18840日=314甲子周。

另一结果是d2=705月=57年。在不定方程中x=8，y=1，z=2。因19×3=57故必有7×3=21闰，有

d2=57×12+21－u+v=705，即v=u。说明凡过57年出现同朔之闰月，其闰月数应相等。因此这是同月同朔干支的周期问题，它同时满足性质一和性质二。事实上57年=26年+31年=321月+384月 =705月，是将两者堆叠而成的。

在57年中应有45谐月，这时d2=705月=660平月+45谐月=20820日=347甲子周。

以下举出3例：

晋武帝末年太熙元年（290）闰五月己丑朔，经51年至晋成帝咸康七年（341）闰十二月己丑朔，历638月，两闰月份相差为7个月；

唐玄宗天宝十三年（754）闰十一月壬戌朔，经52年至唐宪宗元和元年（806）闰六月壬戌朔，历638月，两闰月份相差为5个月；

汉宣帝地节元年（前69）闰正月己巳朔，经57年至汉成帝延元年（前12）闰正月己巳朔，历705月，两闰月月份相同。

当然，对于历法系统而言，由于几千年中存在的非历法因素的影响，使得有些性质会有例外。例如王莽建新朝（公元8），下令将当年十二月改为正月，第二年正月改为二月，等，直到莽亡（公元23）。所以在此期间的闰月数要比正常的多1。如莽历闰五月实际是闰四月。

在所考察的1021年中包括性质三在内全部闰月同朔干支相距的年代d均满足57x+52y+51z=d，其中x，y，z为整数，意即d是57，52和51的线性组合，我们已找出考察区间内的全部d值，并求出每个d的（x，y，z）值。这里省略。

例如前文所提到的汉宣帝神爵三年（前59）闰十二月丙申朔，要经过d=533年后，在元徽三年（475）闰三月才出现第二次丙申朔，整个102年中闰月丙申朔才有三次，是闰十二月的只有一次。所以在2200多年中“闰十二月丙申朔”具有唯一性是不奇怪的了。d=533可分解为x=3，y=5，z=2。这种情况并非个别，例如汉成帝永始二年（前15）闰五月甲寅朔，要经过d=635年后，在唐高祖武德四年（621）闰十月才出现第二次甲寅朔，整个1021年中闰月甲寅朔共有两次。可见中国历法朔闰干支纪日法具有相当的特殊性，以前没有被揭示过。这里d=635年可分解为x=3，y=5，z=4。

比57，52和51年小的d值有46年和47年，46年可分解为x=-1，y=1，z=1；47年为x=-1，y=2，z=0。它们出现的次数仅占全部d值出现总数的2.2％。

对公元前后的年数相加时，因无公元零年，故须将公元前年数绝对值减1后再与公元年数相加。

置闰在制历中占有重要地位。太初元年（前104）之前，汉承秦制，以十月为一年之始，而将所有闰月排在岁尾，称之谓“后九月”。以后历法进步，按“无中（气）置闰法”（不详论），要据当时观测、计算的结果来确定哪个月为闰月，后人所推出的历谱就出现了不同的结果，如陈垣《二十史朔闰表》与刘曦叟的《长历》就有诸多闰月记载不合；另外出土文物的记录又出现于历谱不合的情况，成为年代学研究中较突出的一个问题。所以有必要对闰月朔干支的周期性花费较多篇幅进行研究。上述必要条件还不是充分的，要作出置闰确否的判断需要用综合的方法，特别是要注重出土文物和史书的记载。

例如诸历表均记神爵元年（前61）闰四月壬午（19）朔。但以下证据证明此年应闰三月壬子49朔：

①“神爵元年四月壬午朔己酉46佐解事敢言□”（居延汉简109.7号）。按照当时记录闰月的习惯，只写“闰月”，不写“闰几月”。故此简壬午决非闰月朔，它表明应是闰三月壬子朔。

②陈梦家先生说：“居延汉简10.27，5.10，332.26，10.33，10.30，10.32，10.29，10.31等八简是相联的一册，记神爵元年二月至五月诏书之下达，其闰月丁巳54、庚申57皆属于闰三月壬子49朔”。［18］

③“四月廿九日庚戌47寝兵五月大辛亥48一日壬子49夏至”（下略，居延汉简179.10号）。此简可据“五月大辛亥一日（朔）”按性质二参照伴出纪年简的上下时限考为神爵元年，也可据“壬子夏至”周期性得出相同的结论。它表明非闰四月。

④《汉书·王子候表第三》载：“新利候偃胶东戴王子神爵元年四月癸巳30封”（《汉书》2册493页），表明该年非闰四月。

⑤应用数字方法，从集合论的角度看，用“相连两历法月同属奇（或偶）集其间必有闰月”的判定法则（不详论），可确知是年闰三月。综上，前61年当闰三而非闰四，诸表皆误。

作此修改之后，经过108年，到东汉光武帝廿四年（公元48）闰十月才出现壬子朔，d=108分解为x=1，y=0，z=1，说明这样的修改满足上述必要条件，从一方面证明它的可信度。

史学中立论与驳论有严格要求，证“无三不立，无五不驳”，要驳倒成论须有大量可靠证据。

五、干支历特有的年朔序与分至八节的周期性质

性质四、如果某两年的年朔序相同，则这两年相隔31n（n=3，4，6，7，10，13，14，17，20，21，24，27，…）年。其中n=4，7，10，14，较多，n=7最常见。

所谓年朔序，指一年中朔日干支序列。例如据陈垣表汉高祖元年（前206）的年朔序为：乙卯乙酉甲寅甲申甲寅癸未癸丑壬午壬子辛巳辛亥庚辰，依次是前206年正月到十二月（此处暂不考虑十月岁首的规定）的朔日干支，将它译为字符串，则成52 22 51 21 51 20 50 19 49 18 48 17。将全部历谱的年朔序都译为这样的数串，要问哪一年将和它重复？

我们回答：过961年（=31×31，这里n=31）后，在唐玄宗末年天宝十五年（756）的年朔序和它完全相同。初看起来令人难以置信：时隔近千年，其间出现各种历法30余种，而且756年是著名天文学家一行改用《大衍历》的末年。

其实年朔序周期出现是较普遍的现象，它一直没有引起重视。每次改历，都要变更朔序，显然对周期性有影响；但这种性质突破各历的差别，总会顽强地表现出来。不以大时段历法的共同规律为研究对象则不能对它作出合理的解释。本文是首次论述这些周期性质。

根据性质二，同月同朔干支可能会在31n或31n5年后（n=1，2，…）重现。年朔序相同就是要求一年各月朔干支皆同，条件更严，31n年成了必要但非充分的条件，进而须对n作限定。其周期性十分复杂，可用对历谱进行统计分析的方法。我们选取从公元前206年到公元805年的1010年作为考察区间，从三方面进行研究：①找出所有重复的年朔序；②对不同的再现周期进行分类统计；③建立一个模型解释统计现象。

结论是：在1010年中年朔序重复者有264例，涉及36年，占35.74％；同时，共有649个年号在千年之内保持年朔序的独特性、唯一性，占64.26％。将年朔序相同的公元年数写在括号内，将重现周期（年数）写在括号前，按n值从小到大排到，每个n值只举1例，有

这个表并没有写完；还有个别特例。限于篇幅，不赘。

把这些n值不同的年朔序作分类统计，可知它们出现的频数各不相同，最常见的是n=7即相隔217年，可举出98例，占264例的37.1％，其他依次为n=4（占12.1％），n=17（占9.85％），n=10（占9.47％）和n=14（占8.71％）。如果x，y为整数，则值一般满足3x+4y=n,|x－y|≤2。

事实上除n为几个常见值外，其他值都是据此推算出来。例如对x=5，y=3，有n=27；带着“可能在837年（=31×27）后年朔序重现”的正确信息，才能发现从西汉惠帝二年（前193）过837年后到唐太宗贞观十九年（645）年朔序重复出现。其他如当x=1，y=2时n=11；x=2，y=3时n=18等因出现频数较小，或有其他个别例外。

中国历史上有多少不同的年朔序？这个问题还是未知的。当修改了某年某月朔干支，可能出现新的年朔序，但是独特的年朔序占60％多，重现的年朔序占30％多，大体是不会改变的。了解这一基本知识可以使我们避免年代考证中的错误。包括一些著名的国学大师如罗振玉（1866-1940）、王国维（1877-1927）在内，因为忽略了年朔序的周期性，对敦煌汉简中两枚历谱简年代的确定，均推迟了217年（=31×7），这在年代学中当然是不能允许发生的。

第1枚简：疏勒298号［7］（斯坦因编号）释文为：“三日戊寅戊申戊寅丁未丁丑丙午丙子乙巳乙亥甲辰甲戌癸卯”。法国汉学家沙畹（E. Chavannes，1865-1918）和罗振玉［19］均考为永兴元年（153），但实际上应是元康元年（前65）；这两年的年朔序是相同的，相差217年。

第2枚简：疏勒697号［7］（斯坦因编号）释文为：“九月辛丑朔大（中略）辛巳立冬十月十一日乙未”，王国维、张凤认为它是“建安十年（公元205）历”，但应当是永始四年（前13）。［20］

在我们看来，当n=7时31×7（-65，153），（-13，205）只是周期为217年的两例。其实从298号“三日”简不难向前推两天而求出“一日”简的干支序列，即年朔序。它当然与公元153年朔序相同，但这仅是判断年代的必要条件，其充分性并未证明，罗振玉在数学上犯了一个简单的基本错误。我们学习高等数学，重要目的便是提交数学素养和逻辑思维能力。

性质五、分至八节干支的任一个都会在23年，80年或103年重现。

中国传统历法是阴阳合历。“分至”指春分、秋分、夏至、冬至，再加上立春、立夏、立秋、立冬，谓之“八节”，这是“阳历”即太阳历的内容。重现24节气，努力使它平均分布在一个回归年（日）中，即节气的确定应符合太阳的运动，这样耕种收获就不误农时。

《分至八节表》［10］（前1500—公元2050年）载有3550年的2.84万个干支数据，平均每节的每个干支出现59.167次。由于规律性很明显，不必去研究480种不同八节干支的全部，只须追踪其中的几个，就可以归纳出性质五来；也不必列出所有（平均）59个年代，只须选择其中一段，例如：

壬戌春分：-190（23）-167（80）-87（23）-64（80）17（23）40（80）120（23）143（80）223…

甲子秋分：-145（103）-42（103）62（103）62（103）165（103）268（103）371（23）394（80）474（23）497（80）577…

癸巳冬至：-145（23）-122（80）-42（23）-19（80）62（23）85（80）165（23）188（80）268…

其中负号表示公元前，括号内的数字表示括号前后两个年代的差。其规律性一目了然。

很自然要问：为什么会出现性质五的周期呢？23α=8400.5706日=140甲子周+0.5706日，8α=29219.3759日=487甲子周-0.6241日，103α=37619.9465日=627甲子周-0.0535日。

在103年中只有1小时17分4.6秒的误差，历法当然要尽可能与之相合。不同历法、出土文物等对某年八节干支的记录也可能出现差别，但这不会影响性质五的周期性。偶尔有57年的周期，因57α是347甲子周少1.1947日，误差稍大，这就是它在历法中较少出现的原因。

事实上推算出上述几万个八节干支并不难，难的是一旦与文物、史书记载相忤时该如何解释。由于规律性强，可将历史年代划分成若干时段（如秦汉440年可划成三段），选定正确的初值（如前221年的八节干支），代入统一的八节干支算法公式，注意每段的修正值，则可推算出其间任一年的八节干支来。

将性质五应用于简牍等文物的年代考释，以上述居延汉简179.10号“壬子夏至”为例，据《分至八节表》：-164（103）-61（103）43（23）66（80）146…，只有公元前61年（神爵元年）符合此简的年代。据《史记·匈奴传》：太初三年（前102）“使强弩都尉路博德筑居延泽上”；［21］而建武八年（公元32）之后该地屯戍活动急剧减少，只出土了零星分散的纪年简，所以神爵元年前后各103年皆不可能成为此简的年代。

又如上述敦煌汉简697号“辛巳立冬”，有：-196（80）-116（23）-93（80）-13（23）11（80）91（23）114…，其中只有前13年（永始四年）符合此简的年代，较近的公元11年（始建国三年）是王莽时代，与697号其他信息不符。

六、结语

中国传统历法用干支纪年月日时，形成几千年的历谱，包含了每个历法阶段的丰富信息，有的属于天文、观测，有的属于数学、计算，有的属于社会、人事，成为人类珍贵的科学遗产；同时它又是历史研究中必不可少的时间坐标，熟练而正确使用历表是最基本的要求。因此要走进这座宝库需要天文、历法、数学的一些知识。

顾炎武说：“三代之上人人皆知天文”。现代分工和教学的内容使大多数人缺乏起码的天文知识，干支历对青年人也日渐陌生。然而，中国历法已有几千年历史，凡有华人的地方，年复一年隆重庆祝传统的春节、元宵、端午、中秋等节日，将世代相传。

每当提到天文、历法、数学时，学文科的学生不免立即联想到非常复杂的公式、微积分方法等，从而产生畏惧心理。当然现代科学的确有许多领域不受专门训练便不能得其门径而入；但是古人也同样不懂这些，他们却靠坚持不懈观测天象、不断改进算法和进行主要是四则运算而制定了精密的历法，沿用几千年，这是发人深省的。

本文所用的方法属于初等数论的范畴，所提出的渐近分数和性质定理具有实际应用的价值。历法研究一般是根据史书天文律历志对天文常数、观测数据和算法的记载去推算历法，起止时间以某部历法行用为始终，有一定局限性。本文则力图以历法系统为目标，去寻求适合于各种历法的共同规律；［22］由于传统历法不是一个完整的演绎系统，所以将归纳和演绎法相结合，研究统计的规律，推敲建立数学的模型，从而获得一批周期性的结果。我们已据此研究了几百枝简牍的年代学问题，在史学和汉学的专业刊物如《文史》、《敦煌研究》、台湾《汉学研究》上发表，将此性质应用于年代考释初见成效。在人文社会科学中应用数学方法所见多有，体现了数学向文科领域渗透的趋势；而应用初等数论研究历史年代学，也将逐步完善，成为一种可以接受的辅助考释方法。

［1］谢桂华,等编.居延汉简释文合校上册［M］.北京：文物出版社,1987：228.

［2］谢桂华,等编.居延汉简释文合校下册［M］.北京：文物出版社,1987：594.

［3］陈垣.二十史朔闰表［M］.北京：中华书局,1978.

［4］汪曰桢.历代长术辑要［M］//四部备要·子部.北京：中华书局,1936.

［5］班固.汉书第3册［M］.北京：中华书局,1975：848.

［6］北京师范大学国学研究所.武王克商之年研究［M］.北京：北京师范大学出版社,1997.

［7］林梅村,李均明.疏勒河流域出土汉简［M］.北京：文物出版社,1984.

［8］甘肃省文物考古研究所等编.居延新简——甲渠候官［M］.北京：中华书局,1994.

［9］华罗庚.高等数学引论.一卷一分册［M］.北京：科学出版社,1963：63.

［10］张培瑜.三千五百年历日天象［M］.郑州：河南教育出版社,1990.

［11］罗见今.中国历法中的“千闰年”［M］//黄留珠编.周秦汉唐文化研究.第四辑.西安：三秦出版社,2006：1-5.

［12］吕子方.中国科学技术史论文集.上册［M］.成都：四川人民出版社,1983：35-57.

［13］葛真.用日食、月相来研究西周的年代学［M］.贵州工学院学报,1980（2）：81-100.

［14］罗见今.《居延新简——甲渠候官》中月朔简年代考释［J］.中国科技史料,1997（3）：72-83.

［15］罗见今.《居延汉简》中月朔简年代考释［J］.台北：汉学研究，17,1999（2）：169-185.

［16］罗见今,关守义.敦煌汉简中月朔简年代考释［J］.敦煌研究,1998（1）：158-165.

［17］罗见今,关守义.敦煌、居延汉简中与朔闰表不合诸简考释［M］.文史,2000（1）：57-72.

［18］陈梦家.汉简缀述［M］.北京：中华书局,1980：233.

［19］罗振玉,王国维.流沙墜简［M］.京都：京都东山学社, 1914：9.

［20］罗见今,关守义.敦煌、居延若干历简年代考释与质疑［J］.台北：汉学研究,15,1997（2）：37-50.

［21］司马迁.史记·匈奴列传［M］.北京：中华书局,1959：第9册2916.

［22］罗见今.中国历法的五个周期性质及其在考古年代学中的应用［M］//黄留珠主编.周秦汉唐文化研究：第三辑.西安：三秦出版社,2004：6-18.

（责任编辑：戢斗勇jidouyong@qq.com）

The Application of Elementary Number Theory in the Historical Chronology

LUOJian-jin
（Institute for the HistoryofScience＆amp;Technology,Inner Mongolia Normal University,Huhhot 010022,China）

Based on some tools in elementary number theory,such as congruence,asymptotic fraction,the continued fraction Diophantine equation,etc.,this paper analyzes some questions presented in archaeological chronology.Taking Dunhuang bamboo slips,Ju Yan bamboo slips of Han Dynasty,the book“Historical Records”,unearthed relics and historical data as evidence,and the records of“Calendar of Twenty Dynasties in China”and“Calendar in Three Thousand Five Hundred Years”as a database of sun and moon movements, this paper proves and discusses five cycles properties in Chinese calendar so as to clarify the basic principles and methods of the archaeological chronology of mathematics.

Elementary number theory;bamboo slips in Han Dynasty;Chinese Historical Calendar;the cyclical theorems of Chinese calendar;archaeological chronology

K04

A

1008-018X（2015）06-0028-10

2015-09-20

罗见今（1942-），男，河南新野人，内蒙古师范大学教授。