快速定位的QR 码校正方法

王雄华，张 昕＋，朱同林

（1.华南农业大学 理学院，广东 广州510642；2.华南农业大学 图像图形研究中心，广东 广州510642）

0 引 言

在实际应用中，通过手机、摄像机等设备采集快速响应码 （QR code）［1，2］图像信息时，往往会存在光照不均匀、几何形变等情况，给快速响应码的识别带来不便。因此，如何快速有效地提取和识别QR 码成为人们研究的热点。目前已有很多针对QR 码图像不同特性的校正方法，如张名等［3］、陈威兵等［4］利用位置探测图形特性进行顶点定位及校正，熊用等［5］提出的基于相关匹配的QR 码校正方法，以及文献 ［6－8］给出的条码校正识别方法等。通过实验发现，在条码识别应用中，这些校正方法要么在对顶点定位时存在明显的局限性，要么校正所需时间过长，无法满足其实时性的需求。针对条码识读对识别成功率和解码时间等的特殊要求，本文提出一种低复杂度的顶点寻址算法，

1 QR 码图像特征及应用

1.1 QR 码特征

QR 码符号是由正方形模块堆叠而成的正方形阵列码，它由编码区域以及包括位置探测图形、分隔符、定位图形和校正图形的功能图形组成，条码四周有分隔空白区，如图1所示。

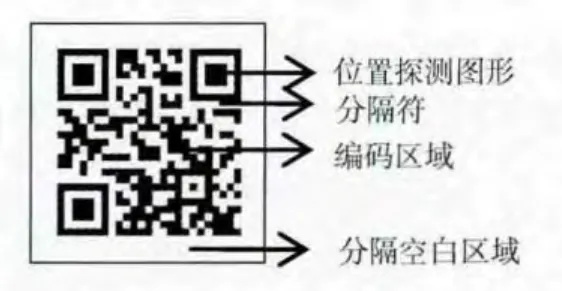
图1 QR 码结构

1.2 图像特征的应用

（1）在实际应用中，QR 码图像四周为一定间距的分隔空白区域。从空白区域自外向内进行行扫描，能快速寻找到QR 码边界的黑色像素点；

（2）3个 “回”字型位置探测图形分别位于QR 码图像的左上、右上和左下位置，通过手机、摄像机等采集QR码图像时，发生一定的几何形变，3 个位置探测图形在图像中的相对位置不发生变化；

（3）位置探测图形与编码区域之间存在一定间距的分隔符，即位置探测图形与编码区域之间没有相邻拼接的黑色像素点。

2 图像二值化

在QR 码识读应用中，能否通过对图像二值化来获取正确的条码黑白模块序列信息是译码正确与否的重要组成部分，因此图像的二值化效果将直接影响到其能否成功识读解码。对图像的二值化首先需要确定阈值的大小，最为常见且有效的全局阈值处理方法是Otsu算法。但手机、摄像机等设备在采集QR 码图像时，容易受外界环境影响而发生光照不均匀现象。这时该方法在背景照明不均匀时有可能失效［10］。本文采用灰度图像形态学法和Otsu算法相结合，从而完成QR 码图像的二值化。

二值化具体步骤如下：①首先对图像进行灰度转换，得到灰度图像；②对灰度图像进行闭运算操作；③将闭运算后的图像减去原灰度图，即做底帽变换；④采用Otsu算法对底帽变换后的图像二值化。

二值化效果如图2所示。图2 （a）为原图，图2 （b）为直接采用Otsu算法处理后的二值化图，图2 （c）为采用灰度图像形态学法和Otsu算法处理后的二值化图。从图2可知，采用灰度图像形态学法和Otsu算法相结合，其二值化效果更好。

图2 二值化对比效果

3 QR 码顶点获取

对条码进行几何校正，首先需要获取失真QR 码图像的4个顶点坐标。实际应用中，在采集QR 码图像时，一般情况下，条码的水平倾斜角不会过大，即发生几何形变时，3个位置探测图形在图像中的相对位置不发生变化。在行扫描进行顶点寻址过程中引入冗余点剔除，能有效地降低冗余点对顶点定位造成的影响，从而准确获取QR 码左上、右上和左下顶点。另外，由于位置探测图形与编码区域之间没有相邻拼接的黑色像素点，通过对边界黑色像素点的等间隔抽样，构造像素点斜率偏离度容错处理判断，可以快速找到第4个顶点坐标。

3.1 快速获取3个顶点

按先后顺序分别从QR 码分隔空白区域的正上，正左，正下，正右，左上，左下，右上7 个方向出发，由外向内进行直线扫描。当直线与QR 码出现至少一个交点时，扫描结束，依次可得到第1，2，…，7 条扫描直线。基于点线相交关系，在7 个方向上，扫描直线与几何失真的QR码有3种出现交点的相交情况，如图3所示。

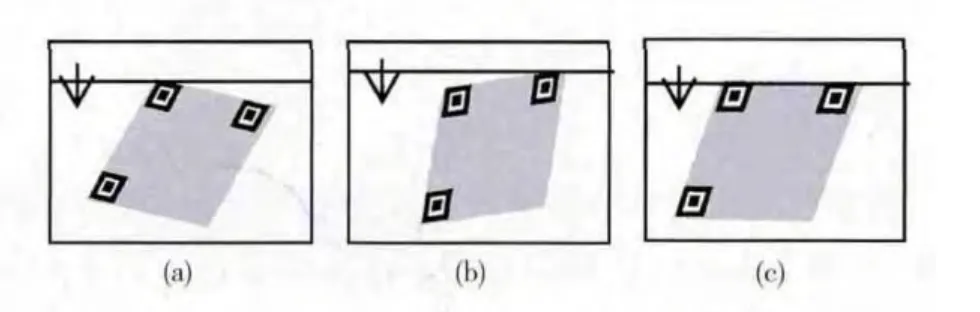
图3 扫描直线与QR 码相交

3种相交情况分别为：图 （a）情况代表QR 码发生顺时针偏转；图 （b）情况代表发生逆时针偏转；图 （c）情况代表QR 码无明显偏转。

当扫描直线与几何失真的QR 码相交属于第 （a）种或第 （b）种情况时，有且仅有一个交点；当相交属于第 （c）种情况时，保留第一个交点和最后一个交点。7 个方向扫描结束后，最多可以得到14个交点。

在实际图像应用中，当扫描直线与失真QR 码边界的斜率较接近或发生像素偏移时，扫描时图3第 （a）种与第（b）种情况也会出现多个交点 （如图4所示），当出现交点个数大于等于2时，保留两个交点 （第一个交点和最后一个交点），并对这两个交点进行冗余点判断与剔除。

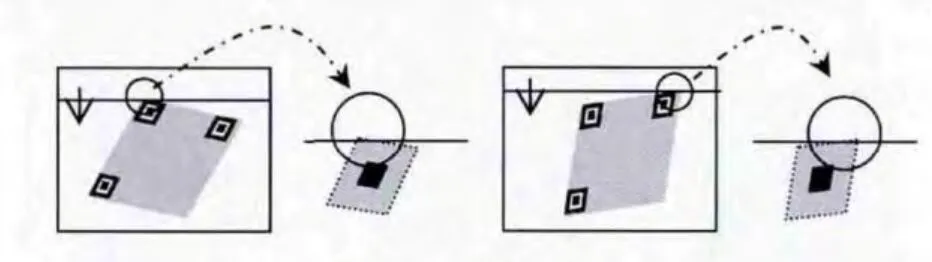
图4 相交点放大

冗余点剔除过程 （redundant－point－elimination）如下：

（1）当从正上方向扫描时，存在图5两种保留两个交点且其中一个是冗余点的情况；

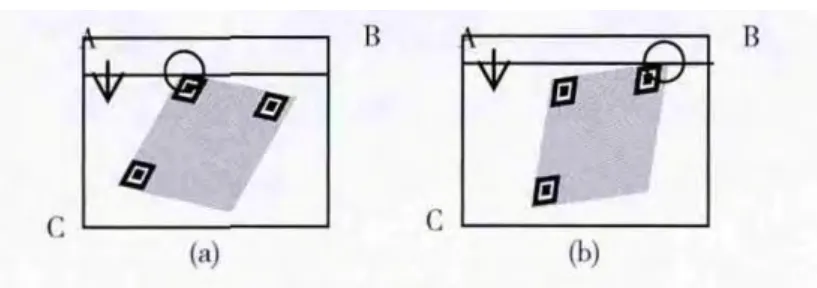
图5 正上扫描两个交点情况

在图5 （a）和图5 （b）中，从正上方向扫描结束时，保留第一个和最后一个顶点，其中一个顶点是冗余点，通过距离最短可剔除该冗余点，图6 （a）和图6 （b）为相应的距离，其中A，B和C分别为图中的角点坐标。由距离判断，A到K1的距离L1小于A 到K2的距离L2，图6 （a）中可剔除冗余点K2；同理图6 （b）中可剔除冗余点K3。

同理，正左，正下与正右方向类似。

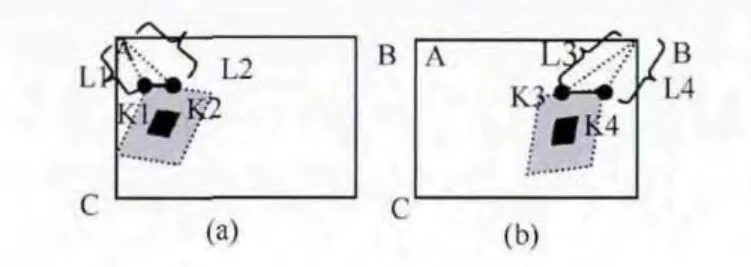
图6 位置探测图形距离

（2）当从左上方向扫描时，只存在图7一种保留两个交点的情况。

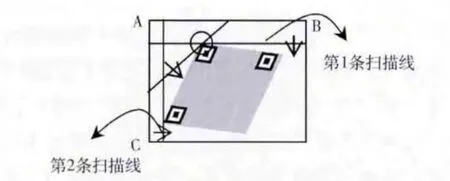
图7 左上扫描两个交点情况

在图7中，从左上方向扫描结束时，保留第一个和最后一个顶点，通过以下规则进行冗余点判断与剔除：①如果两个交点与相邻第1或第2条扫描线的其中一条扫描直线有且仅有一个相交点，则保留该相交点坐标，另一不相交的点坐标剔除；②如果两个交点与相邻第1和第2条扫描线均存在相交点，则保留两个交点坐标；③如果两个交点与相邻第1和第2条扫描线均无相交点，保留两个交点坐标。同理，左下和右上方向类似。

由前文的介绍可知传统校正算法在进行顶点定位时，要么存在较明显的局限性，要么定位所需的时间太长不能满足实时性需求。综合考虑条码校正时顶点定位精确度和实时性的需求，本文基于冗余点剔除过程，提出如下的Find3Vertices算法，用于获取条码左上、右上和左下顶点，具体步骤如下：

步骤1 按先后次序分别从QR 码空白区域的7个方向出发，由外向内进行直线扫描，当与QR 码出现至少一个交点时，扫描结束。

步骤2 当从正上方向扫描结束时，若扫描直线与QR码只有一个交点，则保留该点坐标；若与QR 码存在多个交点，保留第一个和最后一个交点。同理保留正左、正下和正右方向的交点。

步骤3 当从左上方向扫描结束时，若扫描直线与QR码只有一个交点，则保留该点坐标；若与QR 码存在多个交点，则采用本文提出的冗余点剔除过程 （2）选择性保留交点。同理保留左下和右上方向的交点。

步骤4 记步骤2 和步骤3 保留的所有交点为P（xi，yi），i＝1，2，…，k。分别计算P（xi，yi）和图6中角点坐标A（0，0）的距离，与A 距离最近的交点即为左上顶点P1。同理与角点B（0，n），C（m，0）距离最短的交点记为P2，P3。（注：图像大小为m（n））。

步骤5 输出顶点坐标P1，P2，P3，则程序结束。

图8为采用Find3Vertices算法获取9种典型情形的顶点坐标的QR 码图像。

9种典型情形分别为：图8 （a）顺时针小角度偏转，采集角度方向偏右；图8 （b）顺时针较大角度偏转，采集角度方向偏下；图8 （c）顺时针小角度偏转，采集角度方向偏左；图8 （d）顺时针小角度偏转，采集角度方向偏上；图8 （e）无明显偏转，采集角度方向偏左；图8 （f）逆时针小角度偏转，采集角度方向偏上；图8 （g）逆时针小角度偏转，采集角度方向偏下；图8 （h）逆时针小角度偏转，采集角度方向偏左；图8 （i）逆时针较大角度偏转，采集角度方向偏右。

3.2 第四个顶点获取

在QR 码中，由于QR 码右下方属于编码区域，那么在编码时，右下角的第四个顶点可能会出现不存在的情况，因此无法采用本文的Find3Vertices算法获取。

图8 Find3Vertices算法顶点获取

而在QR 码右上方和左下方均存在一个 “回”字型位置探测图形，发生几何形变时，该位置探测图形的边界仍保持近似直线。基于上文已获取的右上顶点坐标P2和左下顶点坐标P3，通过对边界黑色像素点等间隔抽样和像素点斜率偏离度容错处理判断，采用最小二乘法来获取第四个顶点坐标P4。

FindtheForthVertex算法步骤如下：

步骤1 采用Find3Vertices算法获取QR 码右上顶点P2（xB，yB）和左下顶点P3（xC，yC）。

步骤2 以P2为基准点，从P2右方的分隔空白区域出发，往下隔5行进行由外向内的水平扫描，当与QR 码边界的第一个黑色像素点Pi（xi，yi）相交时，扫描结束，并将坐标Pi存入数组V。

步骤3 计算斜率L＝ （yi－yB）／ （xi－xB）。

步骤4 以Pi为基准点，往下隔5行继续进行水平扫描，当与边界的第一个黑色像素点Pi＋1（xi＋1，yi＋1）相交时，扫描结束。

步骤5 计算斜率L1＝ （yi＋1－yi）／ （xi＋1－xi）。

步骤6 如果偏离度｜L1－L｜≤0.5，则Pi＋1加入数组V，重置Pi＝Pi＋1，L＝L1，返回步骤4。否则输出数组V。

步骤7 同理，以P3为基准点，可求取QR 码下方边界黑色像素点数组W。在计算斜率时，由于其分母会出现0的情况，这里先对像素点做90°旋转，即计算斜率的倒数1／L2。

步骤8 分别对数组V 和W 采用最小二乘法求取直线方程，输出两条直线方程的相交点P4，则程序结束。

图9为采用FindtheForthVertex算法获取图8所示情形的第4个顶点坐标的QR 码图像。

图9 FindtheForthVertex算法顶点获取

4 QR 码校正实现

本文采用逆投影变换对几何失真的QR 码进行坐标变换，变换公式如式 （1）所示

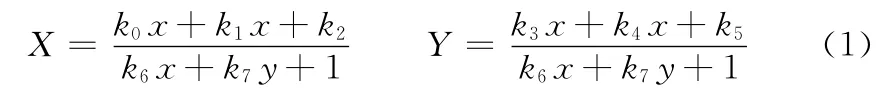
其中，（X，Y）为几何失真的QR 码坐标，（x，y）为校正后的正方形图像坐标。将失真图像中的4 个顶点P1，P2，P3和P4还原成正方形图像顶点P1’，P2’，P3’和P4’，整理可得

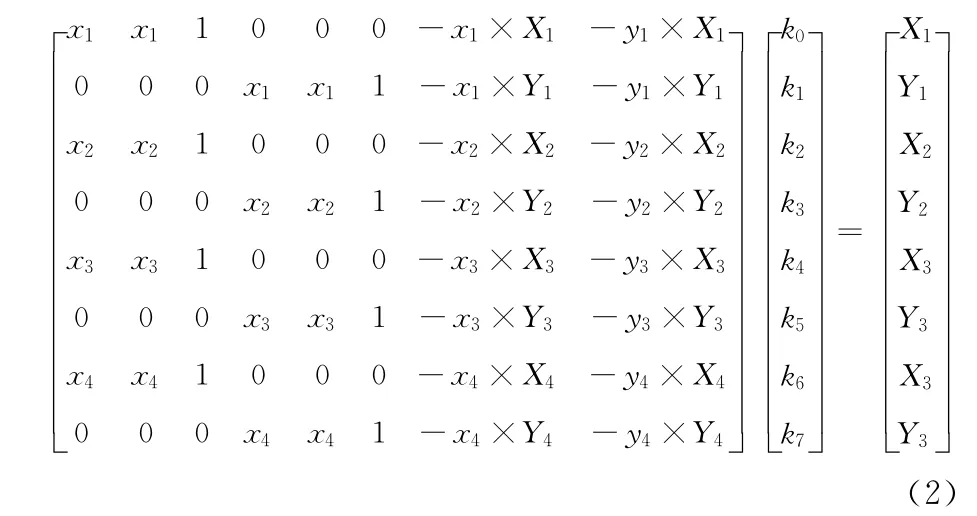
式 （2）中k0～k7未知参数可从上述方程组联合求解得到，从而实现从不规则四边形到正方形的坐标变换校正。

但由于式 （1）中计算得到的 （X，Y）一般不是整数，即校正后QR 码在原失真图像中所对应的像素其坐标不是整数。而计算机只保存整数坐标的图像像素值，这会导致校正后的坐标在原图中，也无法获取准确的灰度值。这时需要采用灰度插值。常见插值方法有最邻近插值，双线性插值和双三次内插。本文折中采取双线性插值完成图像的像素值填充，如图10 （b）所示。

从图10 （b）可看出，校正后的QR 码边缘存在较明显的锯齿化，不利于信息准确提取。由于QR 码模块规模一般至少为3×3像素单位，故这里构造光滑算子边长为3的方形结构元，依次采用数学形态学法的开运算和闭运算对图像进行边缘平滑［10］，得到最终的校正图像，如图10（c）所示。

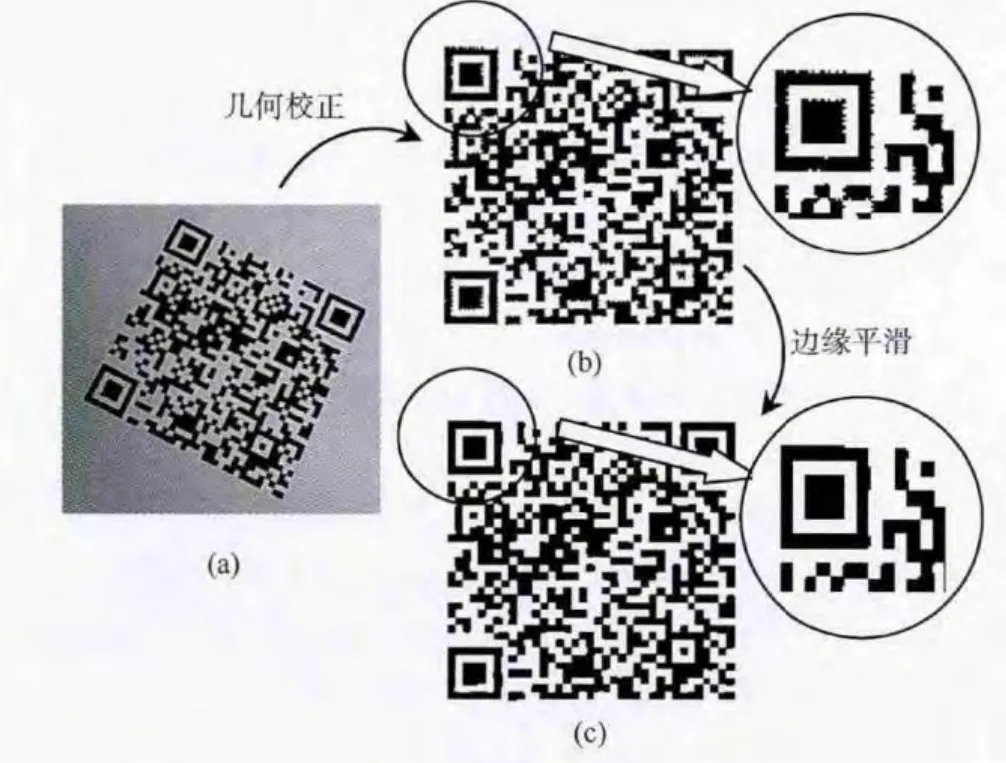
图10 校正效果

5 实验结果与分析

为了使实验更加具有普遍性，本文采用较为广泛的聊天摄像头 （30万像素）进行条码图像采集。本次实验共采集到480幅分辨率为640×480的QR 码图像，其中拍摄角度方向偏上、偏下、偏左和偏右分别120 幅，实验环境设计如下：①条码模块像素点规模变化，采用模块像素点分别为3×3，5×5的QR 码；②条码模块数变化，采用模块数分别为21×21，25×25，…，49×49等8种常见的QR码；③光照不均匀变化，采用偏亮和偏暗的光照环境。在AMD Athlon X2 2.80GHz的计算机上对收集的QR 码图像，采用本文算法在Matlab软件上进行校正测试。实验数据见表1。

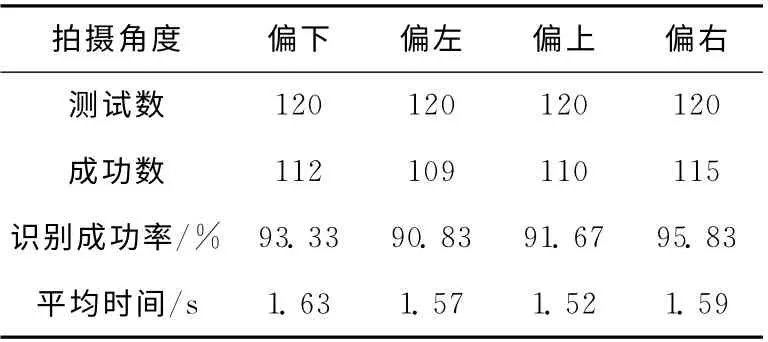
表1 实验数据统计结果

传统算法在对QR 码进行识别定位时，一般采用Hough变换进行边缘检测或者基于位置探测图形中1∶1∶3∶1∶1的深浅模块交替排列特征进行顶点定位。由于QR码边界不连续，采用Hough变换检测边缘往往误差较大，另外，Hough变换直线检测法属于穷尽式搜索，难于满足QR 码识别实时性的要求。而当采集装置与条码平面的相对角度过大时，在位置探测图形中，深浅模块1∶1∶3∶1∶1交替排列的特征也无法得到保证。

相比较于传统算法，本文算法在对QR 码进行顶点定位时，避免了Hough变换等高运算量方法，从QR 码的图像特征出发，提出一种低复杂度的顶点寻址算法，能准确获取到失真图像的顶点坐标，经过校正与译码处理，平均识别成功率达92.9%，平均处理时间为1.58s，远高于国标QR 码校正检测方法71%的平均成功率［5］。其中部分图像无法正确识别的主要原因有：①由于拍摄QR 码时距离过近，图像出现模糊重叠现象，导致部分信息丢失；②在强光下，曝光过度的QR 码图像二值化不能达到很好的效果，导致顶点寻址时无法准确定位。

图11为采用本文算法校正的部分QR 码图像。

图11 校正效果

6 结束语

针对采集QR 码图像发生光照不均匀、几何形变等情况，提出了一种校正算法，能够有效地克服各种明暗光照影响问题，快速获取到失真条码的顶点，使整个算法能够在相对短的时间内达到较高的校正识别成功率。通过对实际QR 码图像的测试不难看出，该算法抗环境干扰能力较强，在进行行扫描时引入冗余点剔除过程，能有效降低冗余点对顶点定位造成的影响，同时结合边界像素点间隔抽样和斜率偏离度容错处理，对不同拍摄角度方向的图像都能取得较好的顶点定位，为后续的QR 码校正及识读提供保障。同时该算法校正所需的时间较短，满足了QR 码识读应用对实时性的需求，因此可应用到包括嵌入式、手持式终端设备等的条码识读应用中。

［1］XU Ling，JIANG Xinzhi，ZHANG Jie.The design and imple－mentation of mobile QR code identification system ［J］.Journal of Computer Application，2012，32 （5）：1474－1476 （in Chinese）.［徐玲，蒋欣志，张杰.手机二维码识别系统的设计与实现 ［J］.计算机应用.2012，32 （5）：1474－1476.］

［2］LIU Ningzhong，SU Jun，SUN Han.Industrial control environment QR Code detection and recognition algorithm ［J］.Journal of Electronic，2011，39 （10）：2459－2463 （in Chinese）.［刘宁钟，苏军，孙涵.工业控制环境中QR Code的检测和识别算法 ［J］.电子学报，2011，39 （10）：2459－2463.］

［3］Chen Changsheng，Alex C Kot，Yang Huijuan.A two－stage quality measure for mobile phone captured 2D barcode images［J］.Pattern Recognition，2013，46 （9）：2588－2598.

［4］ZHANG Ming，ZHENG Jianli.QR code recognition algorithm based on the characteristics of symbols ［J］.Computer Engineering，2011，37 （4）：278－280 （in Chinese）.［张名，郑建立.基于符号特征的QR 码识别算法 ［J］.计算机工程，2011，37 （4）：278－280.］

［5］CHEN Weibing，YANG Gaobo，FENG Lu.A complexity image preprocessing methods of QR code［J］.Journal of Hunan University，2012，39 （10）：93－97 （in Chinese）.［陈威兵，杨高波，冯璐.一种QR 码识别的低复杂度图像预处理方法 ［J］.湖南大学学报 （自然科学版），2012，39 （10）：93－97.］

［6］XIONG Yong，WANG Lucai，AI Qionglong.QR code identi－fication method based on correlation matching ［J］.Chinese Journal of Scientific Instrument，2011，32 （3）：571－576 （in Chinese）.［熊用，汪鲁才，艾琼龙.基于相关匹配的QR 码识别方法 ［J］.仪器仪表学报，2011，32 （3）：571－576.］

［7］SUN Ming，FU Longsheng，YANG Xinting，et al.Automatic recognition of QR code image analysis method ［J］.Journal of University of Electronic Science and Technology，2009，38（6）：1017－1020 （in Chinese）.［孙明，傅隆生，杨信廷，等.用于QR 码自动识别的图像分析方法 ［J］.电子科技大学学报.2009，38 （6）：1017－1020.］

［8］YANG Jiali，GAO Meifeng.A QR code pretreatment method［J］.Computer Engineering，2011，37 （2）：218－220 （in Chinese）.［杨佳丽，高美凤.一种QR 码预处理方法 ［J］.计算机工程，2011，37 （2）：218－220.］

［9］Wu Bangzheng，Zhong Shangping.A distortion rectification method for distorted QR code images based on self－adapting structural element［C］／／8th International Conference on Wireless Communications，Networking and Mobile Computing，2012：1－6.

［10］Gonzalez Woods.Digital image processing ［M］.3rd ed.RUAN Qiuqi，RUAN Yuzhi，transl.Beijing：Publishing House of Electronics Industry，2011 （in Chinese）. ［冈萨雷斯.数字图像处理 ［M］.3 版.阮秋奇，阮宇智，译.北京：电子工业出版社，2011.］