基于区间向量抽象域的数值程序分析算法

吴世堂，李 宁，詹海潭

（中国航天科技集团公司第七一○研究所，北京100037）

0 引 言

程序中变量的值范围信息有助于判断程序中是否存在除零错误、数组越界、整数溢出等多种运行时错误。精确获取变量值范围是不可能的，必须在精度和效率之间进行折中。基于抽象解释理论［1］的数值程序分析技术可以给出每个程序点的数值变量近似且可靠的值范围信息。其中基于该理论的抽象域的设计是权衡分析精度和效率的关键。

在航天控制软件中，往往需要进行大量矩阵运算，因此对矩阵的抽象直接影响该类软件的分析。在已有的抽象域中，有许多对数组的抽象，为了降低分析的复杂性，提高分析效率，一般是将整个数组简单抽象为单个数值变量，即不考虑数组元素之间的差异性；或者将数组元素抽象为固定数目的几个数值变量［2］，每个部分用一个数值概要变量来抽象，有限考虑了元素之间的差异性，但是仍然极大损失数组元素精度；还有的提出数组区间集的方式来抽象数组元素［3］，通过在整型区间集的基础上构造数组区间集记录数组变量值范围和数组长度信息，增加了空间开销；侯苏宁等提出将数组中的每个元素均抽象为一个数值变量［4］，虽然提高数组元素分析的精度，但是分析效率极低，并不适合实际航天控制软件的分析［5］。

本文在充分考虑对航天控制软件分析中矩阵运算的精度重要性，以及分析效率，提出了区间向量抽象域。通过将矩阵的各行各列分别抽象为一个区间，形成一个区间向量对，用区间向量对的对应元素交集表示矩阵元素。同时，设计了一系列域上的操作算子保证分析的精度和效率。本文方法与将矩阵抽象为单个变量方法和抽象为简单几个变量方法相比，精度有了很大的提高；与完全展开矩阵每个元素的方法相比，大大减少时间和空间开销，增加了方法的实用性。

1 区间向量抽象域

1.1 区间向量抽象域的表示

区间向量抽象域是在经典的区间抽象域基础上，针对程序中的数组变量的表示而进行的扩展。下面先回顾区间抽象域的定义。

区间抽象域是指用值区间来描绘程序变量值范围的抽象状态。其符号通常可以表示为Internal＝ ｛⊥｝∪｛［m1，m2］｜m1≤m2，m1∈M∪ ｛－∞｝，m2∈M∪ ｛＋∞｝｝。对任意m∈M，都可以将m 的大小扩展到 （－∞，＋∞）上，即－∞≤m≤＋∞。

基于区间抽象域［6］的静态分析是在所有程序点为每个变量维护一个区间，用来刻画变量在该程序点的值范围信息。

为了更准确的描述变量的值范围，很多研究提出区间集的概念［7］。但是仍然没有区别数组元素之间的差异性，仅仅将数组变量作为单独变量来处理相对应的区间集，对于分析数组元素运算所带来的精度损失仍然很大。

矩阵元素是实数集的有序集合，而区间向量［8］是区间集的有序集合，能够合理的表示矩阵元素的有序性，在程序静态分析中就能够体现元素之间的差异性，在提高分析的精度的同时，分析的效率也不会过于复杂，满足实际软件分析的需要。

对于给定的矩阵 （数值型二维数组）A 中假设包含m×n个元素，那么首先可以将实数矩阵转化为区间矩阵，然后将矩阵中每一行的n 个区间元素由该n 个元素可能取到的最小值和最大值所构成的区间来近似表示。将矩阵中每一列的m 个区间元素由该m 个元素可能取到的最小值和最大值所构成的区间来近似表示。因此，一个矩阵可以由一个列区间向量＝［A1A2… Am］T和一个行区间向量＝［Ar1Ar2… Arn］所组成的区间向量对＜，＞来近似表示，其中向量中的元素Ai（i＝1，2，…，m）是矩阵A 的第i 行元素抽象后的形式化表示，Ajr（j ＝1，2，…，n）是矩阵A 第j 列元素抽象后的形式化表示。

由于区间抽象域［5］在实数R 上的区间集合构成了一个完全格，显然，区间向量的集合也构成了一个完全格［Itvects，iv，∩iv，∪iv，⊥iv，┬iv］。基于抽象解释理论，实数矩阵与区间向量对抽象域之间的关系可以通过下面Galois连接来表示

式中： （R）——实数集合，I——区间集合， ——矩阵。具体函数γiv是将区间向量抽象域向矩阵具体域进行具体化的过程，形式化表示为γiv＝［〈ItvectsT，Itvects〉→ （I（（R）））］，具体化过程是通过将行、列两个区间向量对应的区间元素求交集获得矩阵中的相对应的矩阵元素，形式化定义如下所示

抽象函数αiv是将矩阵具体域向区间向量抽象域进行抽象化 的 过 程。形 式 化 定 义 为αiv＝ ［ （I（ （R）））→〈ItvectsT，Itvects〉］，抽象化的过程是通过首先将实数矩阵转化为区间矩阵，形式化表示为： （ （R））→ （I（（R）））。然后将区间矩阵的每一行的所有区间元素的可能取值的最小值和最大值作为一个区间，表示该行所有元素的可能取值的上界；每一列的所有区间元素的可能取值的最小值和最大值作为一个区间，表示该列所有元素的可能取值的上界。这样就形成一个区间向量对来实现矩阵的抽象过程。形式化定义如下所示

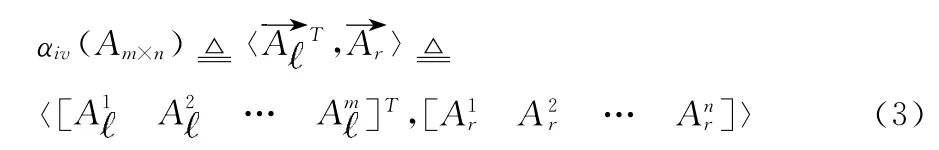
1.2 区间向量抽象域的域操作

在基于抽象解释理论框架下，抽象域是主要内容，而支撑抽象域的各种基本操作算子是抽象解释框架中的抽象域应用于实际程序分析的关键。下面给出在上面定义的区间向量抽象域上基本操作算子的设计。

设任意给定两个实数矩阵Am×n 和Bn×t，通过上面设计的抽象化函数αiv，可以获得抽象区间向量对分别为

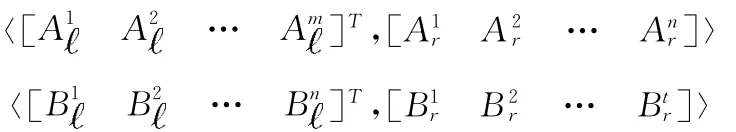
区间向量抽象域是对实数矩阵转化为区间矩阵后进行的抽象，也就是对区间抽象域进行的扩展，因此，在区间向量抽象域上的操作算子也与区间抽象域操作算子密切相关。下面分别详细给出该抽象域上的基本操作算子的设计。

（1）交操作 （Meet）

两个区间向量之间的交运算是指两个矩阵的相对应的两个元素区间值范围进行交运算。具体过程为，首先根据区间向量对进行具体化操作，分别获得两个区间矩阵，然后对获得的两个区间矩阵相对应的元素求交运算。那么矩阵Am×n和Bn×t单个元素Aij和Bhk交运算的形式化定义如下所示

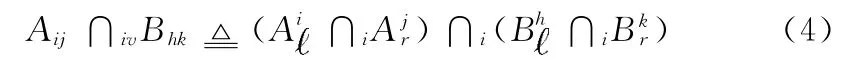
式中：∩i运算是区间抽象域交操作，即两个区间进行交操作。

（2）接合操作 （Join）

两个区间向量进行接合是指两个矩阵的相对应两个元素区间值范围作并运算，具体过程为，首先根据区间向量进行具体化操作，分别获得两个区间矩阵，然后对获得的两个区间矩阵相对应的元素求接合。那么矩阵Am×n 和Bn×t单个元素Aij和Bhk接合运算的形式化定义如下所示

式中：∪i运算是区间抽象域接合操作，即两个区间进行接合操作。

（3）算术运算操作 （Arithmetic）

两个区间向量的算术运算操作是指两个矩阵的相对应的两个元素区间值范围作算术运算。具体过程为，首先根据区间向量对进行具体化操作，分别获得两个区间矩阵，然后对这两个区间矩阵相对应的元素进行相应的算术运算。那么矩阵Am×n和Bn×t单个元素Aij和Bhk算术运算的形式化定义的四则运算如式 （6）所示

其中，运算符⊙i∈｛＋i，－i，×i，÷i｝，均为区间抽象域上进行加、减、乘、除四则运算。

如式 （7）为对矩阵Am×n 单个元素Aij取反运算的形式化表示

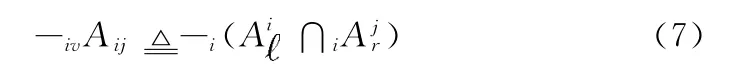
其中，运算符－i为区间抽象域上的取反操作。

（4）比较操作 （Compare）

比较是指格上的两个数之间偏序关系的比较。两个区间向量之间的比较操作是指两个矩阵相对应的元素区间值范围的比较。具体比较过程为，首先根据区间向量抽象域进行具体化操作，分别获得相应区间矩阵，然后对区间矩阵对应的元素进行区间抽象域上的比较操作，形式化表示如下

其中，i是区间抽象域上的比较操作。（5）拓宽操作 （Widening）

在基于抽象解释理论进行程序静态分析过程中，为了加速程序分析的收敛速度，需要对抽象域进行拓宽操作。而对表示矩阵的变量进行拓宽操作可以表示为对区间向量对的拓宽操作也就是分别对行区间向量和列区间向量进行拓宽操作。区间向量的拓宽操作则是将两个区间向量对应元素之间分别进行区间拓宽操作，区间向量对拓宽操作的形式化表示如下

其中，运算 i 是区间抽象域上的标准拓宽操作。（6）迁移函数 （transfer function）

在基于抽象解释的程序静态分析过程中，迁移函数是指，程序在执行完一条语句之后，程序状态发生的变化在抽象域上所表示的状态迁移动作。

基于抽象解释的程序静态分析，会在每个程序点创建一个抽象环境，用X＃表示，即把所有程序变量映射到抽象域。对于C语言中的基本类型的变量都可以映射到区间抽象域，但是对于表示矩阵的变量，在实际程序中并不存在直接矩阵类型，而往往是使用数组表示。矩阵运算操作的完成也是通过若干次的数组元素运算来完成。下面讨论使用二维数组表示矩阵，且程序中采用数组下标访问方式对数组元素进行操作情况下的区间向量抽象域上的迁移函数的操作。

在程序分析过程中，数组的下标需要映射为区间抽象域，对程序中访问矩阵某个元素操作采用如下的方式作为该元素的稳定上近似，即取下标区间内的所有区间元素的最小上界。假设数组行下标变量，列下标变量，那么有

在程序分析过程中，访问二维数组的单个元素时取A［i］［j］＝Ai∩iAjr。如果i⊥i或者j⊥i，则Ai，Ajr⊥i，使用前必须先判断交集是否为⊥i。下面给出针对C语言程序分析过程中需要使用到的各种迁移函数的详细设计。

赋值迁移函数 （assignment transfer function）

对于程序中矩阵元素的赋值语句A［i］［j］＝expr在抽象环境X＃下，程序的状态发生变化，矩阵元素值需要更新，反应在区间向量抽象域中则需要更新区间向量对中相应的元素，赋值迁移函数形式化定义如下

其中，［expr］＃X＃表示程序在某程序点对应的抽象环境X＃下计算表达式expr所得到的区间抽象值。

测试迁移函数 （test transfer function）

对于程序中矩阵元素相关的测试语句A［i］［j］ test，（其中 ｛≤，≥｝）在不同的测试分支中，相关矩阵的状态不同，因此，在不同分支中矩阵元素的值范围需要进行相应的更新，在抽象域中表现为更新区间向量对中相应元素的值。

由于抽象环境X＃中存放该程序点中所有变量的抽象域，因此，此时的抽象环境中对应矩阵元素的抽象域表示有X＃（A［i］［j］）＝〈Ai，Ajr〉，其中假设区间向量抽象域中相应的元素表示为，且有Ai是矩阵相应元素值范围的上近似，test表达式计算出的区间假设表示为test［c，d］。

那么针对程序中测试语句≤和≥分别有式 （12）、式（13）实现区间向量抽象域元素状态的迁移

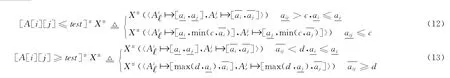
上式中各变量在区间抽象域上的关系如图1所示。

图1 区间关系

2 实验与实验结果分析

本文实验基于开源的编译器前端goto－cc［9］（支持嵌入式C）及开源的数值抽象域库Apron［10］，开发了面向嵌入式C数值程序分析原型工具。

goto－cc是由牛津大学Daniel等开发的编译器，用于将嵌入式C程序编译成控制流图。本文实验是在该编译器生成的控制流图上利用抽象解释理论框架求不动点实现对程序的静态分析。

Apron 是由法国INRIA 开发的一个开源数值抽象域库。为程序分析工具开发者提供一个通用的抽象域独立的接口，可以通过接口直接使用其中已有的抽象域，还为新抽象域的开发提供通用的设计接口。本文的区间向量抽象域就是基于Apron 库提供的接口设计和实现的。

本文实验基于的环境是：Ubuntu 10Linux操作系统，2G 物理内存，1.70GHZ双核CPU 处理器。本文抽象域的实现及与已有方法的对比实验均是基于该环境。

图2给出一个从实际嵌入式C 程序抽取出一个简单的有代表性的矩阵加法的程序片段，为方便精度比较，给二维数组赋值为简单的数值。并且，在不动点迭代时为了不让拓宽操作影响各方法分析精度，这里循环展开次数设为3次，拓宽延迟1次。

下面对各主流对矩阵抽象方法的实验结果进行比较。Blanche提出将矩阵所有元素抽象为一个变量方法 （下文简称单变量法），无法刻画元素之间的区别，无法描述矩阵元素的有序性，计算结果虽是矩阵所有元素的上近似，精度损失很大。侯苏宁提出将矩阵每个元素均抽象为一个变量（下文简称完全展开法），精度损失最小，计算结果与具体域最接近，但是在实际程序分析过程中效率极低，该方法并不实用。本文区间向量抽象域能够较好刻画元素之间区别，在精度损失较小的情况下增加实用性。上述3种方法对数组c实验结果如下所示：

图2 矩阵加法程序片段

单变量法

完全展开法

区间向量法

该程序片段中矩阵加法实际求解结果为：｛｛3，9，6，8｝，｛10，7，14，16｝，｛4，6，10，10｝，｛7，14，11，18｝｝根 据 上 面 的 实验结果，可以看出本文的方法能够稳定且较精确的表示矩阵各元素的值范围。

在空间开销上，单变量法抽象方法简单，对于每个表示矩阵变量的数组变量，无论数组的长度是多大均抽象为单个数值变量，因此，对于一个数组变量仅需要的一个抽象值，空间开销复杂度是一个常数O（1）级。而完全展开法对一个矩阵中的每个元素都用一个抽象值 （区间）表示，抽象值的空间开销是依据数组的元素个数而定的。因此，对一个有m×n个数组元素的矩阵需要的抽象值个数为m×n个，对每个抽象值的表示采用的是区间抽象域那么，空间复杂度是O（m×n）级。本文的区间向量抽象域依据矩阵的各行、各列分别进行区间抽象，即m 行抽象出一个含m个区间元素的区间向量，n列抽象出一个含n 个区间元素的区间向量，需要抽象区间的开销为m＋n个，因此空间开销复杂度为O（m＋n）级。

在时间开销上，单变量法在抽象域对矩阵进行操作时只需要对一个抽象值进行交、接合、拓宽等操作，也不会因为矩阵元素的多少而变化，完成一次对矩阵的操作，只需要执行域上操作一次。需要时间自然最少。完全展开法则在每次进行交、接合、拓宽等操作时都需要对m×n个抽象值（区间）均进行操作，因此，完成一次对矩阵的操作时需要进行m×n次的域上的操作操作，消耗时间最大。本文提出的区间向量抽象域在进行交、接合、拓宽等操作时，仅需要对m＋n个区间抽象值进行操作，即完成一次对矩阵的操作时需要执行域上的操作m＋n次。表1为3种方法比较。

表1 3种方法数据比较

实验结果表明本文提出的区间向量抽象域对矩阵变量进行抽象，在时空效率以及分析精度作了很好的权衡。

3 结束语

本文在经典区间抽象域的基础上，提出针对矩阵运算的区间向量抽象域，综合考虑数组元素运算的精确性以及计算的效率。将一个矩阵 （二维数组）抽象为两个区间向量，将矩阵每一行元素抽象为一个区间获得一个区间向量，将矩阵每一列元素也抽象为一个区间获得另一个区间向量。在程序中访问某个元素时，根据数组下标，由行号索引该元素所在行的抽象区间，由列号索引该元素所在列的抽象区间，那么两个区间的交集作为该元素的近似。能够体现元素之间的差异性且较精确的表示数组元素，同时，在时间和空间消耗上取得合理的权衡。实验分析结果证实区间向量抽象域对矩阵运算的精确性以及实用性。

［1］Cousot P.Formal verification by abstract interpretation ［G］.LNCS 7226： NASA Formal Methods. Norfolk， USA：Springer Berlin Heidelberg，2012：3－7.

［2］Gopan D.Numeric program analysis techniques with applications to array analysis and library summarization ［D］.Madison：University of Wisconsin，2007：64－93.

［3］ZHANG Shijin，SHANG Zhaowei.Detection of array bound overflow by interval set based on Cppcheck ［J］.Journal of Computer Applications，2013，33 （11）：3257－3261 （in Chinese）.［张仕金，尚赵伟.基于区间集的Cppcheck数组边界缺陷检测 ［J］.计算机应用，2013，33 （11）：3257－3261.］

［4］HOU Suning.Research on value range analysis based on abstract interpretation ［D］.Changsha：National University of Defense Technology，2009 （in Chinese）.［侯苏宁.基于抽象解释的数值程序分析技术研究 ［D］.长沙：国防科学技术大学，2009.］

［5］HOU Suning，CHEN Liqian.A static analyzer for numerical programs in C and Fortran ［J］.Computer Engineering ＆Science，2011，33 （3）：94－102 （in Chinese）.［侯苏宁，陈立前.一个面向C和Fortran数值程序的静态分析工具 ［J］.计算机工程与科学，2011，33 （3）：94－102.］

［6］JIANG Jiahong，CHEN Liqian.Floating－point program analysis based on floating－point power set of intervals abstract domain［J］.Journal of Frontiers of Computer Science and Technology，2013，7 （3）：209－217 （in Chinese）.［姜加红，陈立前.基于浮点区间幂集抽象域的浮点程序分析 ［J］.计算机科学与探索，2013，7 （3）：209－217.］

［7］WANG Yawen，GONG Yunzhan.A method of variable range analysis based on abstract interpretation and its applications［J］.Chinese of Journal Electronics，2011，39 （2）：296－303（in Chinese）.［王雅文，宫云战.基于抽象解释的变量值范围分析及应用 ［J］.电子学报，2011，39 （2）：296－303.］

［8］ZHANG Jianhua.The global optimization algorithm using interval mathematics and its application research ［D］.Hefei：Hefei University of Technology，2012 （in Chinese）.［张建华.基于区间数学的全局优化算法及其应用研究 ［D］.合肥：合肥工业大学，2012.］

［9］University of Oxford.Goto－cc－a C／C＋＋front－end for Verification ［EB／OL］. ［2014－03－19］.http：／／www.cprover.org／goto－cc.HTM.

［10］Jeannet B，Mine A.The APRON library for numerical abstract domains ［C］／／Proceedings of the 21st International Conference on Computer Aided Verification，2009：661－667.