基于遗传算法的电动助力转向系统控制策略研究

张建威，辛世界，曲宝军

ZHANG Jian-wei, XIN Shi-jie, QU Bao-jun

（山东理工大学 机械工程学院，淄博 255000）

0 引言

近年来，由于科学技术的飞速发展，汽车电子技术也得到了巨大的进步，人们对汽车转向系统（Steering System）的也提出了越来越高的要求。由于原来使用的机械液压助力转向系统、电控液压助力转向系统存在着液压系统无法避免的缺陷，如液压油泄漏、零部件较多、养护成本较高等，遂逐步的发展为电子助力转向系统[1]。

EPS具有结构简单、易于养护、控制性能好等优点而被越来越多的汽车厂商采用安装，同时也成为汽车新技术的研究热点。目前国内对EPS控制方法的研究主要有传统的PID控制、模糊自适应PD控制、基于PD的H∞控制等[2]。但都存在一定的问题，例如传统的PID控制精确度越来越无法满足人们的需求、模糊自适应PD控制其算法复杂，对EPS硬件要求较高等。而遗传算法具有算法简单，易于实现，仅使用适应度函数进行约束，而适应度函数又无需连续可微等优点，本文拟采用基于遗传算法的PID控制，对EPS建立控制模型，对车体利用系统空间状态模型模拟，并进行仿真分析。

1 EPS机械结构及其数学模型

1.1 EPS机械结构

EPS的机械结构主要是由转向盘、转向柱、扭矩传感器、减速机构、助力电机、ECU等组成，对其进行适当简化后得到其机械结构简图如图1所示。

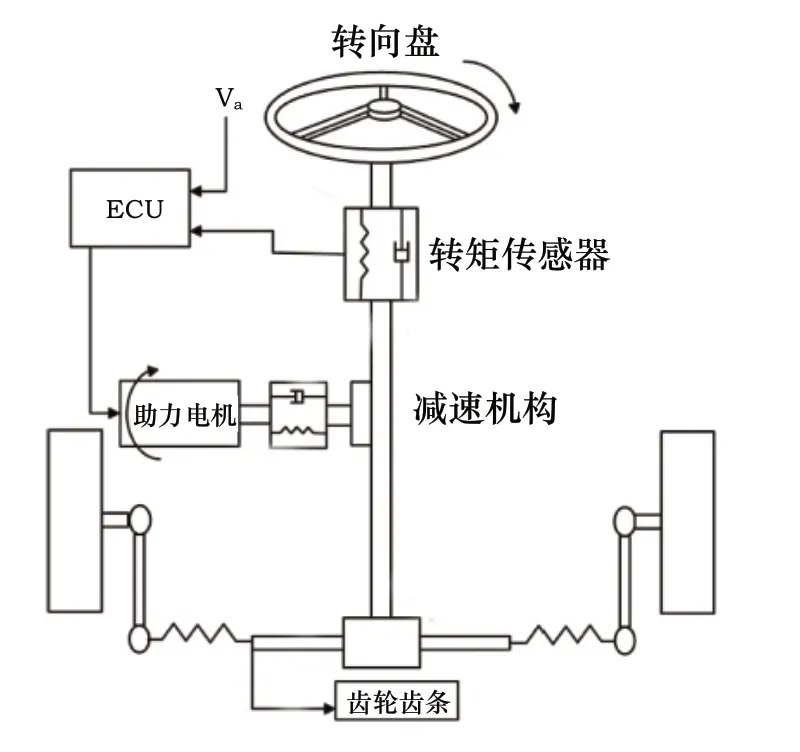
图1 EPS机械结构简图

1.2 EPS数学模型

根据牛顿力学、运动学定律，得出转向盘及上转向柱、齿轮、齿条的动力学方程为[3]：

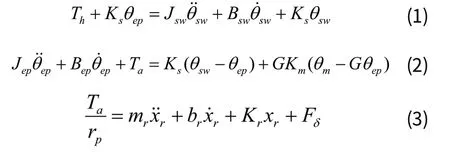
为了方便分析，假定小齿轮和输出轴之间是由等速万向节连接的，则有进而由式(2)、式(3)得：

其中，Th、Ta分别为转向盘输入扭矩、输出轴上的反作用扭矩；Jsw、Jep分别为转向盘及上转向柱的转动惯量、齿轮齿条转动惯量；分别齿轮转角、方向盘转角、助力电机转角；mr、xr、rp、br、Be、Kr分别为齿轮齿条质量、齿条位移、齿轮半径、齿条阻尼系数、减速机构阻尼系数、轮胎与地面摩擦系数：G、Km、Ks、FδF分别为减速机构减速比、助力电机刚度系数、扭杆的刚度系数、路面阻力。

由于在整个EPS中，助力电机的作用及其重要，而且也是我们控制的主要对象，下面单独对助力电机进行建模。本文采用的是直流永磁电机，额定电压为12V，额定电流为65V，扭矩系数为Ka，反电动势常数为Kb，转速为N时：

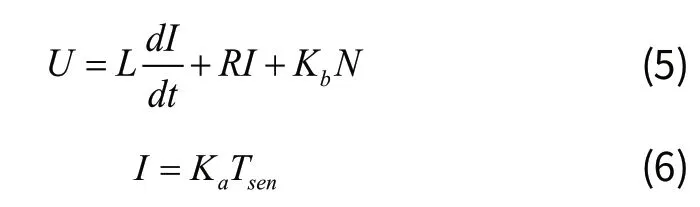
当电机稳态时有L=0，此时电机的数学模型可化为：

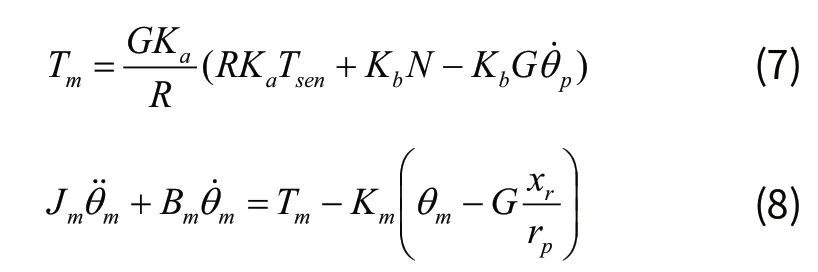
其中Tm为助力电机输出转矩；Jm、Bm分别为助力电机转动惯量、助力电机阻尼系数；Ka为助力增益，是速度与助力的函数，表现为不同速度下的不同助力特性；Tsen为扭矩传感器检测到的扭矩。

2 控制算法及控制策略

EPS对输入信号的响应是通过ECU对助力电机的控制实现的，其流程为：首先ECU通过扭矩传感器获得扭矩信号和车速里程表的车速表（也可安装单独更精确的车速传感器）获得实时车速信号，然后通过实时在线的遗传算法优化PID参数，得出最优解，PID控制器根据相应的PID参数产生相应的控制电压，然后助力电机根据相应的电压，产生相应转速及转矩。

其PID控制公式为：

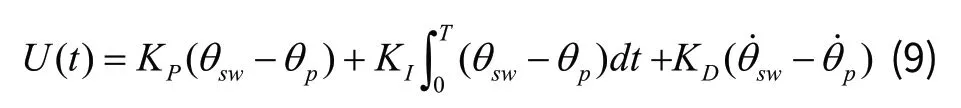
由于遗传算法无须对目标函数微分，也不用了解被控对象，非常适于解决本文这种复杂的非线性模型，且遗传算法相对简单，对硬件要求较低，其鲁棒性也较好，对于系统稳定性有很大的保证。故本文选择了遗传算法优化PID控制器参数。使用MATLAB内置的遗传算法工具箱GATOOL，用MATLAB Function模块实现其优化。本文仅对适应函数进行分析。

适应函数，又称评价函数，其构成了群体任一个体的生存环境，个体的适应值决定了其在此环境的生存能力的强弱，适应值越大，生存能力越强。由于适应值是判断群体中任一个体生存能力强弱的唯一确定性依据，所以，它的选择直接决定了最终结果的好坏[4]。由于本文遗传算法模块的目的是根据PID控制器的输入e(t)和输出u(t)的值来优化计算出PID控制器的参数KP、KI、KD，为了得到较为满意的过渡过程动态特性，采用ITAE（时间加权的误差积分准则），同时为了避免控制量过大和超调，引入PID控制器输出的平方项u2(t)和惩罚功能，对于惩罚功能，即当系统发生超调时，超调量参与性能指标的评价。最终选取的评价指标为：

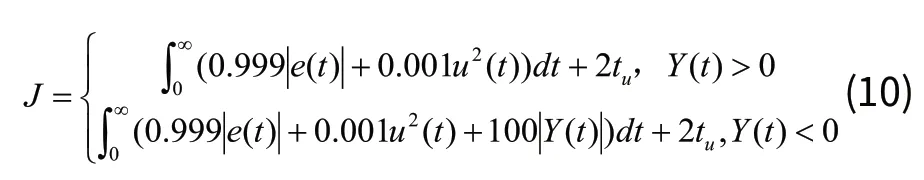
其中e(t)为系统误差，u(t)为PID控制器的输出，Y(t)=y(t)-y(t-1)，y(t)为被控对象的输出，tu为阶跃上升时间。

显然J>0，所以适应度函数为：

使用MATLAB仿真结果如图2所示。

下一步根据式(1)、式(4)、式(7)、式(8)、式(9)可建立起EPS的状态空间方程：

图2 遗传算法优化PID参数阶跃响应

3 建立仿真模型及仿真结果分析

3.1 建立仿真模型

在MATLB/Simulink中建立EPS控制仿真模型时必须考虑实际工况所带来的问题。

1）转向盘的频繁抖动所带来的助力电机频繁起停的问题。助力电机频繁的起停，容易造成助力电机发热量过大带来不稳定性因素，也对其寿命影响较大，为了避免这个问题，控制中加入死区控制模块，即设定限值Tmin，只有当Tsw≥Tmin时，助力电机才开始工作。

2）遇到紧急情况，驾驶员紧急转向造成的助力电机瞬时电流过大的问题。瞬时电流过大，易损坏电机，导致短路，使转向系统无法获得助力，对安全造成极大的威胁。为了避免该问题，加入饱和度模块，即设定限值Tmax，当Tsw≥Tmax时，助力保持恒定，以此限定最大电流的范围。

3）其他随机信号带来的干扰问题。尤其车辆行驶的路况是随机，车辆轮胎等车况也是随机的，这就给转向控制带来了随机的噪声干扰，本文采用带限白噪声模块来模拟。

所建立的EPS控制器的模型如图3所示。

3.2 仿真分析

如图4(a)为转向盘角阶跃输入时常规的PID参数整定下的小齿轮转角的响应曲线；图6(b)为遗传算法优化PID参数下的小齿轮转角的响应曲线，可以看出，经过遗传算法的优化，其波动性尤其是初始响应时的波动，其幅度明显变小，得到较大的改善，也变得更为顺滑，操作更为平稳，从开始响应到平稳的时间也变得更为短暂，其灵敏性得到了提高。

图3 EPS控制器仿真模型

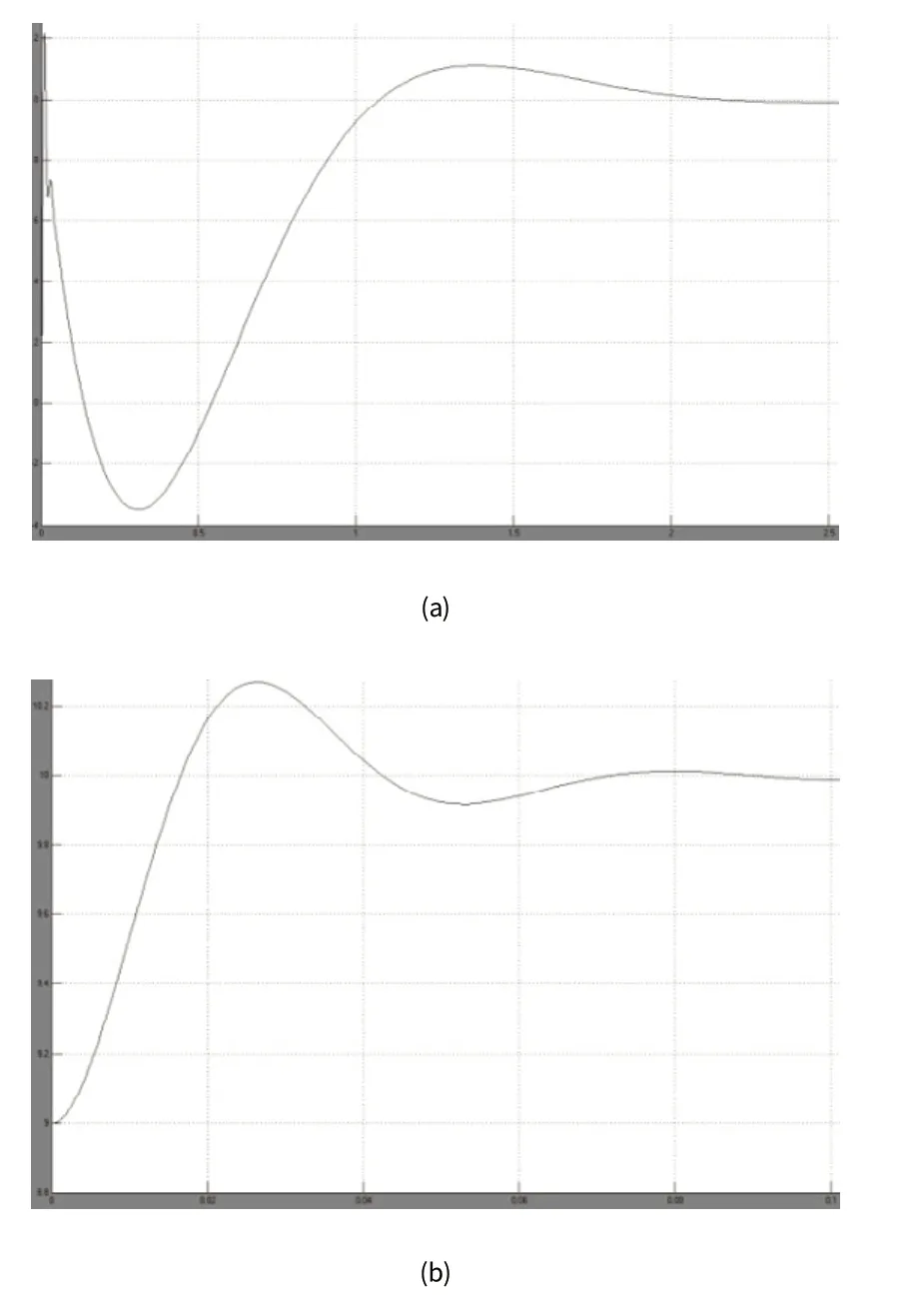
图4 转向盘角阶跃输入时，小齿轮角响应图

如图5(a)转向盘角阶跃输入时常规的PID参数整定下的汽车横摆角响应，图5(b)为遗传算法优化PID参数下的汽车横摆角响应。汽车横摆角的角速度（竖坐标）反应了汽车在转向时，控制器对其的反应速度即灵敏性，其响应时间（横坐标）反应其可靠性，从图4可以看出优化后，其灵敏性和可靠性都得到了提升。

4 结论

本文根据建立的理想EPS的数学模型，搭建了基于MATLAB/Simulink的仿真控制模型，利用空间状态方程模拟车辆其他模块，进行仿真分析，通过输入转向盘角阶跃信号，分析比较有无遗传算法优化下的小齿轮转角和汽车横摆角得出，本文提出的控制策略行之有效：提高了EPS控制的可靠性以及灵敏性，为进一步开发产品打下了理论基础。

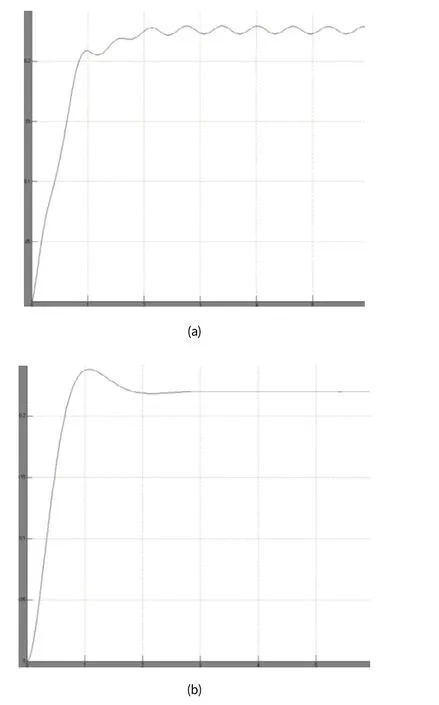
图5 转向盘角阶跃输入时汽车横摆角响应图

[1]胡建军,卢娟,秦大同,李辉.电动助力转向系统的建模和仿真分析[J].重庆大学学报（自然科学版）,2007,30(8):10-13.

[2]晋兵营,宁广庆,施国标.汽车电动助力转向系统发展综述[J].拖拉机与农用运输车,2010,37(1):1-2,5.

[3]吕威.电动助力转向系统稳定性和电流控制方法研究[D].吉林:吉林大学,2010.

[4]陈奎元,马小平,季学武.电动助力转向系统控制技术的研究[J].江苏大学学报（自然科学版）,2004,25(1):21-24.

[5]李敏强,寇纪淞,林丹,李书全.遗传算法的基本理论与应用[M].北京:科学出版社,2002,216-253.

[6]李建新,柳利军.一种基于遗传算法的PID参数的优化控制策略[J].现代电子技术,2005,28(2):14-15,20.

[7]KIM Ji-hoon,SONG Jae-bok.Control Logic for An Electric Power Steering[J].Mechatronics,2002,(12):447-459.