基于马尔可夫模型的无人机路径规划的线性化
【信息科学与控制工程】
基于马尔可夫模型的无人机路径规划的线性化
王社伟,梁国伟,陶军
(空军航空大学,长春130022)
摘要:研究了利用马尔可夫模型对无人机路径规划问题建模,以及马尔可夫模型的线性化问题,提出了离散的马尔可夫模型线性化的方法,并利用数学归纳法进行了证明。仿真结果表明,对状态流程图进行线性化以后,由初始状态到终止状态的每条路径的状态转移概率变得更加直观,能够从状态流程图中清楚地得到各个因素对整个系统任务的影响。
关键词:无人机路径规划;马尔可夫模型;线性化
收稿日期:2014-08-26
作者简介:王社伟(1965—),男,副教授,博士,主要从事容错控制与导航的故障诊断、可靠性分析以及飞行控制系统等研究;梁国伟(1989—),男,硕士研究生,主要从事多无人机路径规划及任务分配研究;陶军(1966—),男,博士,讲师,主要从事智能体控制,无人机任务规划技术研究。
doi:10.11809/scbgxb2015.01.027
中图分类号:V279
文章编号:1006-0707(2015)01-0095-04
本文引用格式:王社伟,梁国伟,陶军.基于马尔可夫模型的无人机路径规划的线性化[J].四川兵工学报,2015(1):95-98.
Citationformat:WANGShe-wei,LIANGGuo-wei,TAOJun.LinearizationofUAVPathPlanningBasedonMarkovModel[J].JournalofSichuanOrdnance,2015(1):95-98.
LinearizationofUAVPathPlanningBasedonMarkovModel
WANGShe-wei,LIANGGuo-wei,TAOJun
(AviationUniversityofAirForce,Changchun130022,China)
Abstract:The linearization of the markov model after building a model for Unmanned Aerial Vehicle (UAV) path planning using the markov model was discussed, and a linearization method was put forward for the discrete markov model, then we proved it by using mathematical induction. The simulation results show that the state transition probability of each path becomes more intuitive from initial state to the end state after the linearization of state flow diagram, and can get very clear impact of each factor on the entire system tasks from the flow diagram.
Keywords:UAVpathplanning;markovmodel;linearization
近年来,无人机的路径规划问题已经成为无人机领域的一个研究热点,是一个具有多约束条件的NP复杂问题。在战场环境中,由于作战的动态性和不确定性以及协同控制的复杂性,使得任务开始后会出现许多预先无法预料的情况,因此,良好的路径规划是无人机顺利完成任务和发挥最大效能的保障和基础。
由于战场环境的连续性,建模时需要将连续的战场环境离散化,其中一种方法是采用路径图的概念,将战场环境抽象为一个图,其节点是空间的自由点,节点之间的边即为无碰撞的自由边[1]。当无人机的当前位置、路径节点和终点确定以后,可以将无人机的路径规划问题看成是时不变齐次的马尔可夫链,其中,无人机当前位置为初始状态,路径节点为模型的状态,任务终点为终止状态。
为了分析比较不同的路径规划方案,常常希望能够从状态流程图中更直观地得到一些主要参数对系统任务的影响。因此,在状态流程图的化简过程中,提出了将系统的马尔可夫模型的状态流程图“线性化”(linearization)的概念[2],这一概念同对控制系统中的非线性系统进行线性化是完全不同的2个概念。对系统马尔可夫模型状态流程图的线性化是指在系统任务分析之前对流程图进行化简,尽量减少除初始状态和终止状态以外的中间状态之间的交叉转移关系。这样尽管会使系统可靠性模型状态数目增加,但不同于状态合并的逆运算,它可以使无人机任务分析变得更加直观方便[3]。
1线性化的基本概念
假设无人机路径规划的马尔可夫模型为时不变齐次的马尔可夫链[4]。图1表示一个普通的马尔可夫模型状态流程图,线性化的目的是将其化简为和原图等价的,其中任意一个从初始状态到达终点吸收状态的路径都没有经过交叉转移的状态流程图,如图2所示。进行线性化的系统状态流程图须满足以下条件[5]:
1) 只有一个初始状态和至少一个吸收状态;
2) 所有的状态转移概率都是时不变的常数;
3) 状态之间的转移关系均为单向的。
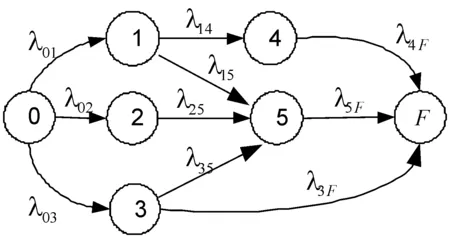
图1 普通状态流程示意图
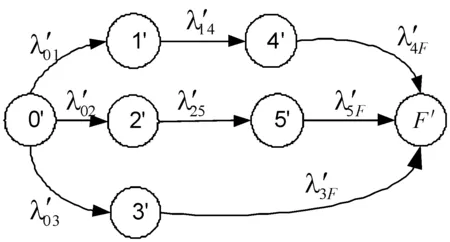
图2 线性化状态流程示意图
为了方便后文分析问题,给出以下概念:
定义1:到达状态流程图中某状态的路径数大于1的状态,称为合并状态。
定义2:状态流程图中某状态可到达的其他状态数大于1的状态,称为分叉状态。
由定义1和定义2可知,在图1中,状态0、状态1和状态3是分叉状态;状态5和状态F是合并状态。在图2中,只有初始状态是分叉状态,终止状态是合并状态。
马尔可夫模型线性化的过程可以分为2步,即合并状态的分解和分叉状态的化简。
2合并状态的分解
如图3所示,对合并状态分解的方法比较直观,其具体的方法是:在整个状态流程图中,将初始状态放在左边,终止状态放在右边,然后由左向右逐一将每个合并状态分解成和其输入路径数相等的一些新的状态,直到最后只有终止状态是合并态为止。例如,在图3中,将合并状态A分解为和其输入路径数M相等的状态X1,X2,…,XM。
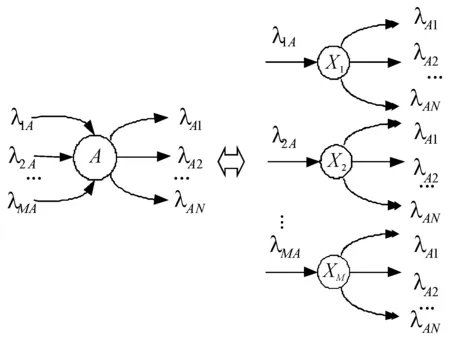
图3 合并状态的分解
3分叉状态的化简
同合并状态的分解相比,分叉状态的线性化相对要麻烦一些。如图4所示,在图4(a)中,马尔可夫模型的状态01,02,…,0M,A,11,12,…,1N在时刻k的状态概率分布向量为:
π(k)=[x01(k),x02(k),…,x0M(k),xA(k),
x11(k),x12(k),…,x1N(k)]
(1)
在图4(b)中,马尔可夫模型状态01,02,…,0M,A1,A2,…,AN,11,12,…,1N在时刻k的状态分布概率向量定义为:
π′(k)=[x01(k),x02(k),…,x0M(k),xA1(k),xA2(k),…,
(2)
如果图4(b)所示模型满足:
1) 状态Aj的初始状态分布概率为:
j=1,2,…,N
(3)
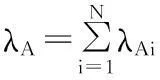
2) 状态0i的状态分布概率x0i(k)同图4(a)所示系统相同,其中i=1,2,…,M。则4(a)中的分叉状态A和图4(b)中虚框内所示部分是等价的。
在式(1)中,图4(a)中的分叉状态A为该马尔可夫模型状态空间中第(M+1)个状态。根据状态概率分布向量的定义和图4(a)中所示的状态转移关系,可得状态A在下一时刻仍保持在原状态的概率为:
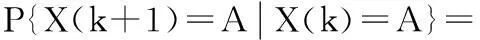
(4)
由图4(a)可知得:
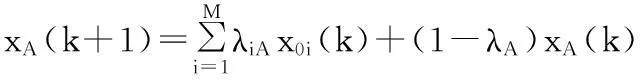
i=1,2,…,M
(5)
x1j(k+1)=λAjxA(k)+(1-λ2j)x1j(k),
j=1,2,…,N
(6)
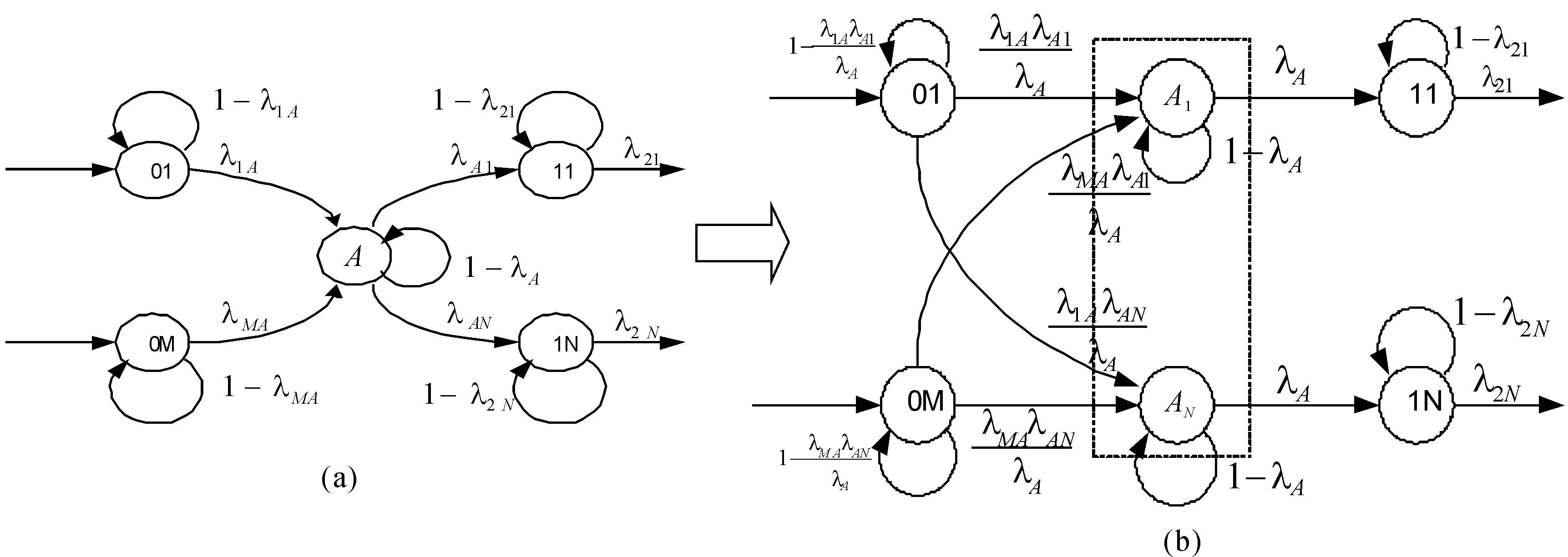
图4 分叉状态的线性化示意图
由图4(b)可得:
i=1,2,…,M;j=1,2,…,N
(7)
j=1,2,…,N
(8)
显然,只要证明式(6)和式(8)等价即可。首先,利用数学归纳法证明:在所示的初始条件下,对于任意的k=0,1,2,…,λAxAj(k)=λAjxA(k)恒成立。
假设当k=0时
由式(5) 、式(7),得
(9)
(10)
其中,i=1,2,…,M; j=1,2,…,N。
所以
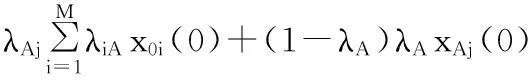
j=1,2,…,N
(11)
j=1,2,…,N
(12)
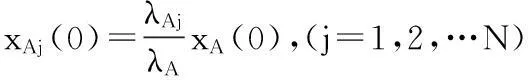
λAxAj(1)=λAjxA(1),j=1,2,…,N
(13)
假设当k=n时
λAxAj(n)=λAjxA(n),j=1,2,…,N
(14)
成立。
则当k=n+1时,分别由式(5) 、式(7)可得
(15)
(16)
其中,i=1,2,…,M;j=1,2,…,N。
所以
(17)
j=1,2,…,N
(18)
将式(14)代入式(17)和式(18),得到:
λAxAj(n+1)=λAjxA(n+1),j=1,2,…,N
(19)
所以,在定理所示初始条件下,对于任意的k=0,1,2,…,λAxAj(k)=λAjxA(k)恒成立。
由上述分析可知,图4(a)中的分叉状态可以化简为图4(b)中的状态。
4仿真实例
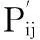
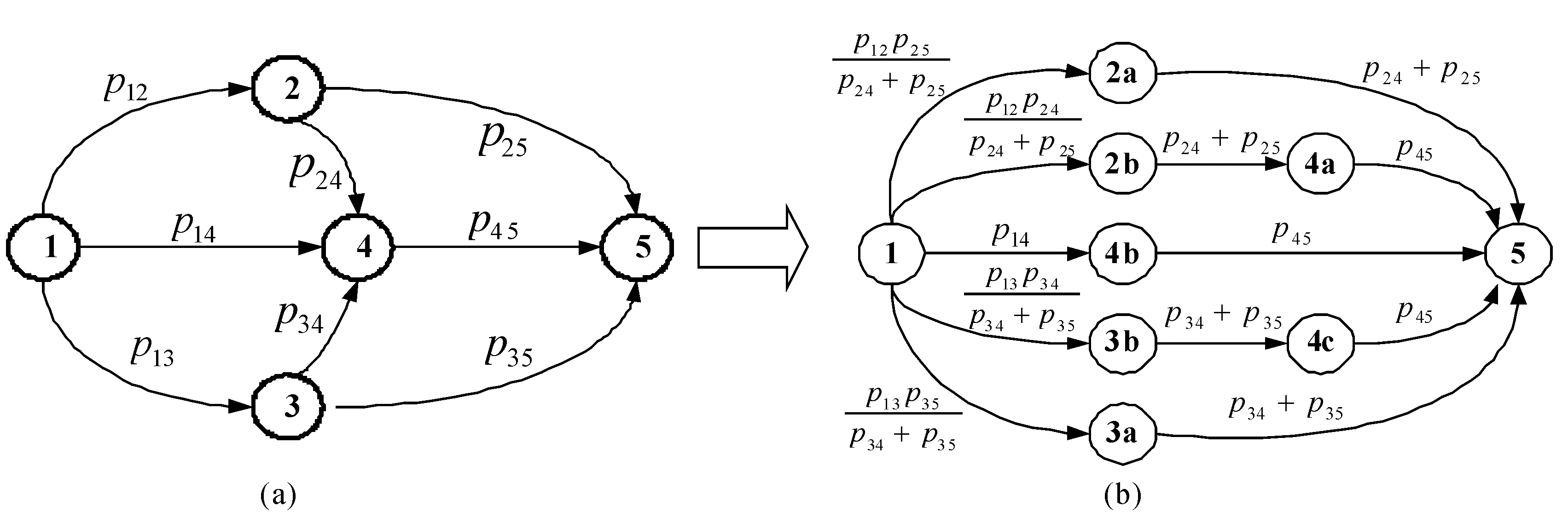
图5 无人机路径规划示意图
按前面所述线性化方法,可以将图5(a)化成图5(b)的形式,其状态转移概率如图所示,每条路径的生存概率和时间如表1所示。

表1 结果统计表
5结束语
将系统马尔可夫模型状态流程图5(b)同5(a)进行比较,虽然用于无人机路径规划的马尔可夫模型的状态数目有所增加,但是分析过程要简单直观许多。对状态流程图进行线性化以后,能够从状态流程图中清楚直观地得到各个因素对整个系统任务的影响,可以在路径规划过程中有针对性地加以改进。
参考文献:
[1]高晓静,陈晓峰,智勇.无人机路径规划中的环境和威胁模型研究[J].航空计算技术,2013,43(3):63-68.
[2]王社伟.容错导航系统的可靠性分析[D].北京:北京航空航天大学,1999.
[3]PattonR,ChenJ,NielsenSB.Model-basedmethodsforfaultdiagnosis:someguide-lines[J].Trans.OnInstituteofMeasurementandControl,1995,17(2):73-83.
[4]PermanM,Senegacnik,TumaM.Semi-Markovmodelswithanapplicationtopower-plantreliabilityanalysis[J].IEEETrans.onReliability,1997,46(4):526-532.
[5]BridalO.Safetyandreliabilityanalysisofrepairablefaulttolerantsystems[J].InternationalJournalofReliability、QualityandSafetyEngineering, 1997,42(3):327-339.
(责任编辑杨继森)


