基于马尔科夫概率跃迁矩阵的消费者偏好分析*
姚 韬
(北京科技大学 东凌经济管理学院,北京100083)
马尔科夫跃迁矩阵用来分析消费者行为由一种状态转移成另一种状态的可能,以预测消费者行为未来走向。Heiko.B(2000)等首次将马尔可夫矩阵应用到消费者偏好研究中,通过统计模型假设,建立非齐次矩阵,从对几种快速消费品的进行排名,对未来的市场发展情况进行了预测[1]。宋波等(2013)通过马尔可夫跃迁矩阵对某种产品市场的战略联盟进行了分析。[2]余典范(2013)用灰色马尔可夫状态链对某产品多数品牌市场占有率进行了预测。[3]肖谦等(2014)通过对马尔可夫状态转移的估算,对我国物流市场转移趋势进行了分析。[4]
本文采用了概率矩阵模型分析消费者偏好,避免了传统线性分析法无法保证跃迁结果的总为非负的弊端,同时,降低了状态跃迁概率计算的繁琐性,通过多次迭代使得模型结果具有稳定性。主要过程是通过抽样调查数据,建立消费者行为内部转移的初始矩阵;然后对偏好的初始矩阵和状态跃迁矩阵进行迭代,将其转化为状态概率跃迁矩阵,并通过PPMCC法对该矩阵的稳定性进行检验。
1 模型的建立
1.1 建立消费者偏好的矩阵模型
假设市场共存在n种消费者偏好,其不同时期偏好变化的跃迁如表1所示。表中Pij表示对同一产品第i型消费偏好由状态1跃迁至状态2时的j型消费偏好;Ai表示消费者时期1对某产品类型的消费量总和,Bi表示消费者在时期2对某产品类型的消费量总和。其中矩阵Pij存在未知量,即表1中隐性数值;Ai、Bi的数据可以通过分层抽样统计获得,即表1中虚点数值。表1可以表示成消费者偏好矩阵P[5]。
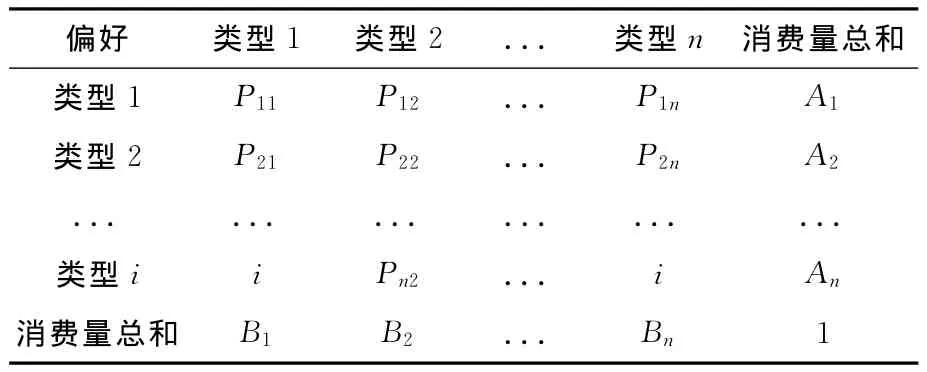
表1 不同时期消费者偏好矩阵
其中,0≤Pij≤1;1≤i≤n,1≤j≤n.
式2中,λ1表示时期1某产品所有偏好类型的消费量;λ2表示时期2某产品所有偏好类型的消费量。
1.2 建立初始矩阵
在消费者偏好方面,一般认为消费者由习惯型和和多变型两部分组成[6],由于这两种消费者的心理因素等原因,导致他们选择产品的偏好不一致。为了构建能反映出消费者对某产品偏好的状态跃迁矩阵,本文假设习惯型为稳定跃迁消费者,多变型为不稳定跃迁消费者,并对这两种消费者群进行抽样统计。
对于稳定跃迁消费者,统计在长期内对某产品不同型号的购买数量x,得到该类型消费者在时期2内的偏好情况,如表2所示。

表2 习惯型消费者的偏好
表2可化成反映习惯型消费者消费偏好的矩阵Px的形式,如式(3):
对于不稳定跃迁消费者,统计其在时期1内某产品不同型号的购买数量y,再通过矩阵跃迁得到其在时期2内购买的数量,如表3所示。其中yij表示在时期1内型消费偏好跃迁为j型的数量。

表3 多变型消费者的偏好跃迁
表3的矩阵表达式,式(4):
再结合稳定跃迁和不稳定跃迁的综合作用,得出消费者偏好跃迁的初始矩阵,见式(5):
其中:α+β=1;分别指习惯性和多变型消费者对消费偏好影响的权重,其值由产品市场的不同特征而定。
1.3 跃迁矩阵“隐性→显性”转化
Pij代表的是消费偏好跃迁矩阵(式1)提高中的隐性数值,而状态初始矩阵(式5)Pk,反映了式1矩阵中隐性数值的内部跃迁。但初始矩阵的缺陷在于,单纯的抽样统计可能导致Ai≠Aki,Bi≠Bkj得到的最终结果误差较大。为了减少初始矩阵的误差,可结合初始矩阵Pk和状态转移概率矩阵P,对Pk逐步迭代求解,转化后的矩阵第i行之和等于Ai,第j列之和等于Bj,该跃迁矩阵的结果更加准确。
第一步,对矩阵Pk进行行变换后转化成式(6)
第二步,对矩阵P(k+1)(式6迭代至第n列变换 ,得式(7):
计算所得式即为式(1)的解。
1.4 概率跃迁矩阵的求法
由式(2)和式(8)可知,时期t的消费者偏好
2 PPMCC法验证“显性”状态跃迁矩阵的稳定性
采用PPMCC(Pearson相关系数法)对求解得到的状态跃迁矩阵P(k+n)的稳定性进行检验。如果跃迁矩阵P(k+n)与初始矩阵P(k+1)的线性相关系数0.8<r<1,表示两矩阵的相关性高,则矩阵P(k+n)稳定。其计算方法如下:
则 P(k+n)和P(k+1)的 Pearson相关系数为:
若0.9<r<1,为极强相关关系;0.8<r<0.9,为强相关关系;-1≤r≤0.8为弱相关关系。
3 实例展示
通过对某产品(汽车)在国内市场的消费偏好抽样调查,其2013年和2014年的数据如表(4)[7]。
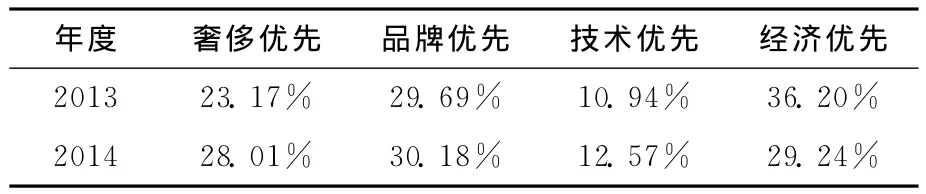
表4 2013年、2014年国内汽车市场消费偏好比例分布
首先,对2013年购买汽车的习惯型(稳定跃迁)消费者购买汽车的偏好进行调查,选取有效样本372个;对多变型(不稳定跃迁)消费者调查,同样选取有效样本372个,可以得到以下分布结果(见表4、表5)。

表5 习惯型消费者偏好分布

表6 多变型消费者偏好分布
对上表列矩阵进行迭代求解可得:
可得:Pk和P(k+n)的Pearson相关系数为:r1=0.9582,r2=0.9282,r3=0.9359,r4=0.9947,以上数据表明,矩阵迭代过程较稳定。
按照式(9),再把 P(k+n)转化成概率跃迁矩阵:
根据式(11)St=λ2Ft,取t=1,2,3,4,即可预测2015-2018年汽车消费偏好比例:
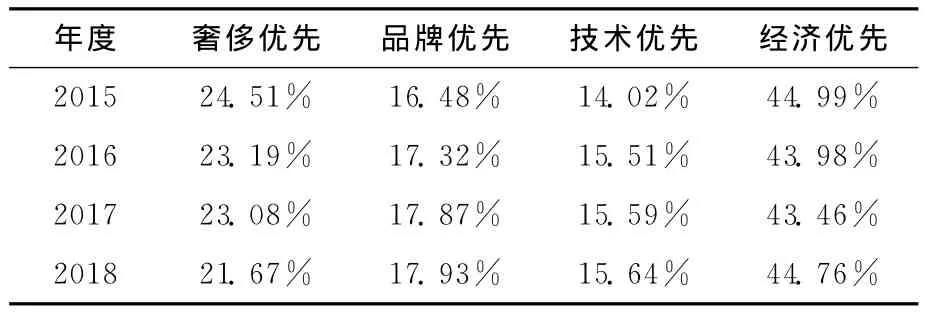
表7 2015-2018年汽车消费者偏好比例预测
4 结论
马尔科夫概率跃迁矩阵和传统的跃迁矩阵相比,能通过对数据的多步迭代,得到更为稳定的预测结果。本文从2013-2014年产品(汽车)消费者偏好入手,先抽样统计获得样本数据和初始矩阵;再通过迭代求解得到了概率跃迁矩阵;接着采用PPMCC法对迭代后的矩阵进行稳定性检验;最后对2015年-2018年产品(汽车)的消费者偏好比例进行预测。结果表明未来四年内,消费者对汽车奢侈优先的偏好逐年下降,而品牌、技术和经济优先的偏好逐年上升,其中经济优先偏好比例上升的最大。
从以上推导和预测可得出以下启示:(1)传统经济学中关于消费者购买长期消费品存在临界点的假设和中国的现状不符。在经济总量处于长期增长的情况下,消费者对长期消费品消费的临界点上也会不断上升,极限会不断延长;(2)生产厂商在制造长期消费品时不仅应该考虑产品的价格和实用性,还要考虑满足如消费者攀比效应的增长带来的差异化需求;(3)长期消费品消费需求波动较大,具有较强的不稳定性。因此,为了避免长期消费品消费的随机性带来的市场冲击,需要政府采取公共政策对消费者进行引导,在整个市场范围内对长期消费品形成示范效应。
[1] Heiko,B.Markov chain models for vegetation dynamics[J].Financial model.,2000,327(3):139-154.
[2] 宋波,徐飞.基于马尔科夫状态转换自发性对称破缺机制[J].系统管理学报,2013,(1):101-105.
[3] 余典范.中国产业动态比较优势的实证研究——基于马尔科夫链的方法[J].经济管理,2013,(12):46-47.
[4] 肖谦,赵海燕.基于马尔科夫模型的物流服务市场占有率的预测[J].湖南社会科学,2014,(4):52.
[5] 聂笃忠,陈桦,米承继等.马尔科夫链状态概率转移矩阵修正算法[J].统计与决策,2013,(3):15-16.
[6] Kim,C.J.Pager,Estimation of Markov regime switching regression models with endogenous switching[J].Journal of Econometrics,2008,143(2):263-273.
[7] 徐长明,李伟利.2013-2014汽车市场分析与预测[J].汽车工业研究,2014,(7):213-217.

