基于模糊结构元方法的船舶航迹拟合
陈婷婷
(上海海事大学商船学院 上海 201306)
基于模糊结构元方法的船舶航迹拟合
陈婷婷
(上海海事大学商船学院上海201306)
摘要在采用船舶AIS数据进行船舶航迹拟合时,传统的航迹拟合方法如最小二乘法或插值法等会平滑掉船舶位置波动的偏差,不能真实地反映出船舶位置的波动现象而失去其意义。提出基于模糊结构元的船舶航迹拟合方法,不仅能够描述船舶位置变化趋势,而且能够直观反映出这种变化趋势的不确定性程度,并通过实例进行了分析验证。
关键词航迹拟合模糊结构元AIS最小二乘法
船舶自动识别系统(automatic identification system,AIS)信息能够直观地反映出船舶的位置变化情况[1],基于船舶AIS数据进行拟合可以获取船舶的航迹线。但是,由于船舶航行受风、流、浪等一些环境因素的影响,尤其是要采取船舶避让行为时,船舶的航迹变化较大,通过AIS观测到的船舶航迹数据点的波动会比较大,数据出现复杂混乱的现象,采用最小二乘法或插值法等一些常用的函数拟合方法将会平滑掉这些偏差,而不能将它们表示出来,这将失去实际的意义,不能反映数据波动现象及其不确定性问题[2-3]。因此,本文提出基于模糊结构元的船舶航迹拟合方法,既能描述船舶位置散点所反映的位置变化趋势,同时还能够反映出变化趋势的不确定性程度。
1 模糊结构元方法
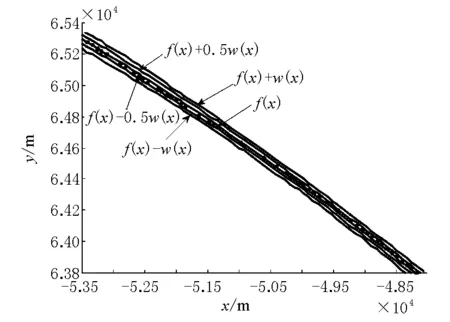
设E为实数域R上的模糊集,隶属函数记为E(x),x∈R,如果E(x)满足下列性质:①E(0)=1,E(1+0)=E(-1-0)=0;②在区间[-1,0)上E(x)是单调递增右连续函数,在区间(0,1]上是单调递减左连续函数;③当-∞ 模糊结构元是R上的正规凸模糊集,是表示模糊零概念的特殊模糊数,它可以具有各种形态。如果模糊结构元的隶属函数在区间(-1,1)上有E(x)>0,且在(-1,0)内是严格单增连续函数,在区间(0,1)内是严格单降连续函数,则称E为正则的模糊结构元。 设模糊集E具有隶属度函数: 通过AIS数据解析得出船舶各点的位置数据x和y值,船舶位置数据点为(x1,y1),(x2,y2),…,(xn,yn),经过经典数据拟合方法可以在直角坐标系中描绘出船舶航迹,得出船舶航迹变化的趋势函数f(x)。 令ω(xi)=|yi-f(xi)|,ω(x),由表1中的数据序列得到。 表1 ω(x)的数据基础 对(xi,ω(xi))(i=1,2,…,n)数据序列进行拟合,确定出模糊度函数ω(x)。 本文选取了上海港长江口深水航道2014年某一天的船舶AIS数据,筛选出其中2条船舶的一段航迹点作为实例分析。Ship1,船长143 m、宽22 m;Ship2,船长200 m、宽32 m。根据实际的船舶AIS数据点,采用传统最小二乘法获取了船舶航迹点的趋势线,采用模糊结构元方法进行了船舶航迹拟合。分别拟合得出2船位置点的趋势函数和模糊度函数。 对于Ship1: f(x)= -6.459 0×10-7x2- 0.381 9x+4.676 2×104 ω(x)= 2.578 6×10-8x2+ 0.001 2x+56.369 2 对于Ship2: f(x)= -8.231 5×10-6x2- 1.119 2x+2.897 8×104 ω(x)= 1.471 4×10-6x2+0.147 3x+ 3.731 5×103+38.311 对Ship1和Ship2分别采用MATLAB绘制曲线,见图1和图2。 图1 基于模糊结构元的船舶航迹拟合(Ship1) 图2基于模糊结构元的船舶航迹拟合(Ship2) 图1和图2中分别给出了λ=0和λ=0.5的拟合效果。当λ=0时,航迹点全部落在上下曲线包围的范围内。从图中可以直观看出船位点的波动情况,上下边界线之间的距离即为船舶的航迹偏移量。模糊度函数值越高,说明船舶波动越明显,则船舶的航迹偏移量就越大,是在研究船舶运行特性时特别值得注意的位置点。且以Ship2为例,通过Matlab计算,上图2中所选取的船舶航迹拟合的模糊度函数ω(x)的最大值是在第2个位置点取得的,最小值是在第156个点取得的,这些特殊点的获取,为研究船舶运动情况以及通航安全等方面提供了参考依据。 本文提出了基于模糊结构元的船舶航迹拟合方法,依据船舶AIS数据获取的船位点进行航迹拟合,并基于MATLAB进行了实例分析。与传统的航迹拟合方法相比,本文提出的方法不仅能够反映出船舶运动趋势线,而且能够直观反映出船位点的波动情况。研究成果能够为船舶运动以及通航安全等方面的研究提供直观的参考依据。 参考文献 [1]张国平,廖任,刘明俊.AIS系统在海事管理中的运动探讨[J].交通科技,2011(3):157-159. [2]刘德浩,王国宏,陈中华.基于数据拟合的航迹关联方法[J].电光与控制,2012,19(4):23-26. [3]罗琳玲,罗克露.基于最小二乘法的K-NN航迹关联算法研究[J].微计算机信息, 2010, 26(1):176-178. [4]郭嗣琮,苏志雄,王磊.模糊分析计算中的结构元方法[J].模糊系统与数学,2004,18(3):68-75. [5]赵宏霞,杨皎平,郭嗣琮.基于模糊结构元方法的模糊线性回归模型[J].辽宁工程技术大学学报,2004,23(3):418-420. [6]何波,郭嗣琮.一种基于结构元理论的系统可靠性计算方法[C].南京:第三届不确定性系统年会论文集,2005:87-93. Ship Track Fitting Based on Fuzzy Structured Element Method ChenTingting (Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China) Abstract: When adopting theship track fitting based on AIS data, the traditional method, such as least square algorithm or interpolation method, would smooth the deviation caused by ship position's fluctuation. This kind of the fitting may lose its significance because the fluctuation phenomenon could not be reflected really and directly. Then, the ship track fitting method based on fuzzy structured element was proposed The method not only described the variation tendency of ship position, but also reflected visually the uncertain degree of this variation tendency.Finally we could analyse and verify the method by an real example. Key words: track fitting; fuzzy structured element; AIS; least square algorithm 收稿日期:2015-05-07 Thinking on Simulation of Drifting Trajectories of Sea Object YeWeiqiang,YuLongfei (Guangzhou Maritime Institute, Navigation Department, Guangzhou 510725, China) Abstract:By analyzing the results of the search and rescue work and the corresponding states of 21st century maritime accidents occurred in china, comparing the relatively research work, the author put forward the ideal of the numerical simulation method for sea crash drift trajectories in different sea area and different sea condition, give the research ideas and procedures to improve and enhance the early maritime search and rescue system. Key words:maritime accident; drifting trajectory; simulation DOI 10.3963/j.issn.1671-7570.2015.04.053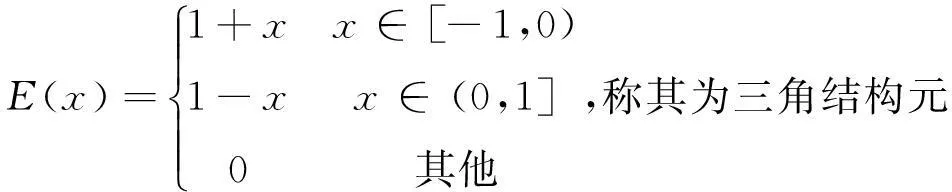
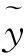

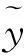
2 基于模糊结构元的船舶航迹拟合实例分析
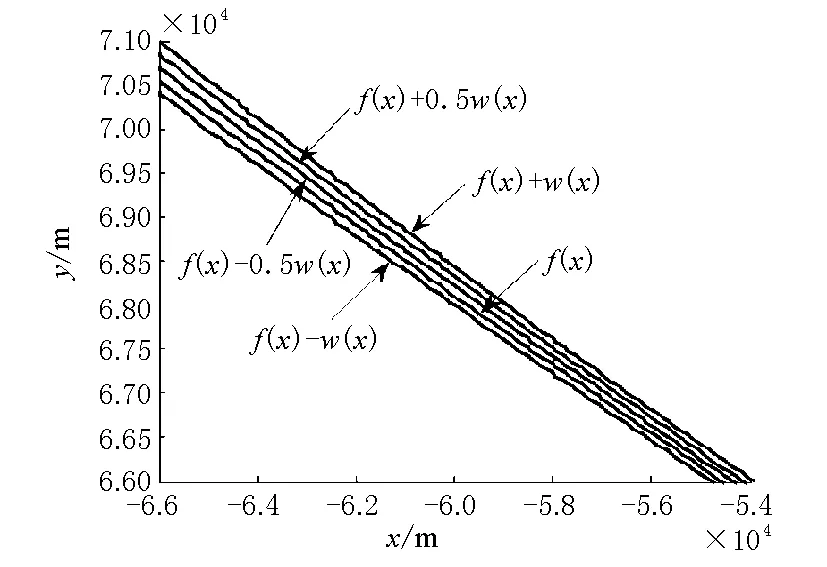
3 结语

