通过增加车道以改善交织区拥堵的可行性研究
陈利霖 龙家彦
(同济大学道路与交通工程教育部重点实验室 上海 201804)
通过增加车道以改善交织区拥堵的可行性研究
陈利霖龙家彦
(同济大学道路与交通工程教育部重点实验室上海201804)
摘要针对短交织区交通拥堵问题,在分析车道的增设方式及其作用的基础上,通过交通供需分析确定交织区拥堵的矛盾所在。以交织车流供需矛盾为研究重点,从微观的角度对交织车辆的换道操作进行剖析,以交织车辆最短换道距离为依据,推算出可增设分流车道的交织区最短长度(26 m)。采用VISSIM仿真,确定增设分流车道后交织车道的通行能力,并将其与交织需求进行对比,来判定可行性。
关键词交通工程可行性供需分析交织区通行能力交织车道
交织区是快速路的重要组成部分,由于城市用地限制等因素造成交织区长度较短(一些甚至已不足100 m),交织问题突出,成为快速路的瓶颈路段。交织区通行能力的影响因素较多,主要有:交织区的长度、车道数、车速、交织比、车型比例、交织区类型。其中,只有车道数是较容易改变的,其他因素都较难改变。因此,目前的工程改造中,为改善交织段的拥堵,通常是增加交织区车道数。然而,由于交织长度并未增加,增加交织区车道数的作用及增加后是否能满足交通需求等问题,需要进行针对性的研究。
与此有关的国内外研究主要集中在交织区的通行能力领域:Ponlathep Lertworawanich和Lily Elefteriadou[1]基于可接受空挡理论和线性规划的方法建立了交织区广义通行能力的模型;钟连德等[2]在分析对通行能力有重要影响的8个参数的基础上,标定了仿真软件CORSIM,得到不同条件组合下的通行能力值;赵靖等[3]以HCM2000中交织区通行能力建议值为基础,建立了通行能力的回归模型;Wa’el H.’Awad[4]采用线性回归和神经网络技术2种方法来计算交织区通行能力;HCM[5]给出了不同类型交织区的通行能力的建议值;刘立英等[6-7]利用仿真数据对Rakha和Zhang提出的交织区通行能力折减系数模型进行了参数标定;Li和Jia[8-9]等利用元胞自动机对含有交织区的交通系统进行了建模,分析了交织区的通行能力和驶入车辆流率和驶出车辆流率的关系,当驶出车辆流率较大时,总流量会减少到较低的值。虽然相关研究较多,但基本上是基于可接受空挡来建立交织区理论通行能力模型,或者通过仿真软件建立交织区通行能力的仿真模型;而没有涉及增加车道可否提高短距离交织区的通行能力,可否缓解交织区拥堵等问题。
由于我国交织区以A类交织区为主,本文将选择A类交织区作为研究对象。以VISSIM仿真软件为工具,来确定增设分流车道后交织车道的通行能力,并将其与交织需求进行对比,从而验证通过增加车道来改善交织区拥堵的可行性。
1 增加车道的作用分析
为了方便说明,将交织区车道分为交织车道(见图1中的车道4、车道5)、直行车道(见图1中的车道1、车道2、车道7)及增设的分流车道(见图1中的车道3、车道6)3类。增加交织区车道的方式有2种:在直行车道侧增设直行车道及在交织车道两侧增设分流车道。增设方式及交通渠化设置见图1。其中:直行车道的通行能力为断面①与断面②的通行能力之和;由于交织车流不管其来自上游哪个车道,其必须执行的换道操作为:从车道4换至车道5或者从车道5换至车道4,所以交织车道的通行能力为车道4与车道5的通行能力之和,即断面③与断面④的通行能力之和。
在交织区长度较短无法增长的情况下,增加交织区的车道便于分离直行车流与交织车流,降低其相互之间的干扰,提高交织区的运行效率。同时,若增加交织区的直行车道,可提高直行车道的通行能力;若增设分流车道,可分流交织车道上已完成交织的车流,使得交织车道上的车流密度下降,车头时距增大,为未完成交织的车流提供了更多换道的机会、腾出了换道空间,提高了换道效率,进而提高了交织车道的通行能力。
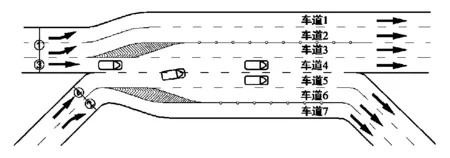
图1 增设交织区车道示意图
2 交织区供需矛盾分析
2.1流量调查
在进行交通供需分析之前,应对交织区交通流量流向进行调查。见图2,交织区交通流向可分为直行流量Q1与Q4,以及交织流量Q2与Q3。一般情况下,流量Q1、流量Q2、流量Q3较大,且相互混杂,直接调查容易混淆,误差较大。本文采用间接的方法来调查流量Q1、流量Q2、流量Q3,调查流程如下。
步骤1。选择3个观测断面(观测断面1、观测断面2、观测断面3)。一般情况下,直行车流Q4较少,单独对其进行调查。
步骤2。同时,在观测断面1统计出流量Q4与Q3之和Q43,则流量Q3为
(1)
步骤3。间接调查流量Q2:在观测断面3统计出Q4与Q2之和Q42,推算出流量Q2为
(2)
由于流量Q4经过观测断面1与观测断面3有个时刻差Δt13,则观测断面3的调查时刻较观测断面1推迟Δt13。Δt13的计算公式为
(3)
式中:l13为观测断面1与观测断面3之间的距离;V4为车流Q4的平均运行速度。
步骤4。间接调查流量Q1:在观测断面3统计出Q1与Q2之和Q12,推算出流量Q1为
(4)
由于流量Q2经过观测断面2与观测断面3有个时刻差Δt23,则观测断面2的调查时刻较观测断面3提前Δt23。Δt23的计算公式为:
(5)
式中:l23为观测断面2与观测断面3之间的距离;v2为车流Q2的平均运行速度。

图2交织区流量流向示意图
2.2交通供需分析
由于交织车流与直行车流在交织区的运行特征完全不同,需单独分析两者的交通供需。设该交织区长度为Lw,一条直行车道的设计通行能力为cs,交织区直行车道数为Ns。则通过查阅HCM(2000),可获得交织长度为Lw,交织流量比为1的2交织车道的通行能力为Cw。
2.2.1直行车流供需分析
交织区直行车道总的通行能力为Cs=cs×Ns。若直行流量Qs≤Cs,则直行车流通行需求能得到满足;若直行流量Qs>Cs,则直行车流通行需求无法得到满足,需增加直行车道数量,增加直行车道的规模为
(6)

2.2.2交织车流供需分析
若交织流量Qw≤Cw,则交织车流的通行需求能得到满足;若交织流量Qw>Cw,则交织车流的通行需求无法得到满足。由于增设分流车道来提高通行能力的效果受多因素影响,不像增加直行车道效果那么显著,需单独对其进行分析。
3 增设分流车道效果研究
增设分流车道的作用为降低交织车道的密度、提高车头时距,为交织车辆提供更多的换道机会。要达到上述目的,交织车辆需在交织区范围内完成交织且成功换道至分流车道。由于车辆换道有最短长度限制,所以要提高交织车道的通行能力交织区必须满足最短长度要求。
3.1交织区需满足的最短长度
分流车道要起作用的条件为交织车辆可在交织区范围内完成2次换道,即交织区的最短长度要求为交织车辆最短换道距离的2倍,其可按下列的方法进行求解:
根据分析,当车辆轴距为len,见图3,则转弯半径的简化计算公式为
(7)
式中:β为前轮与前进方向夹角,其最大取值为25.9°[10];len为车辆轴长,由于快速路上以小汽车为主,其取2.6 m。
如图3所示,当目前车身航向角为α,则与前轮转向角有关的收角距离为
(8)
同理,可获得
(9)
在调整阶段,车身的航向角已经归零是交织车辆的换道距离L取得最小值时必须满足的条件之一。当调整阶段车身的航向角已经归零时,则有
(10)
式中:Llane为车道宽度,一般快速路交织区车道宽度取3.5 m。
由此,可求得换道距
(11)
式中:lcar为车辆长度,由于快速路上以小汽车为主,其取5 m。
则,交织车辆最短换道距离min(L)为在满足式(12)条件下式(11)取得的最小值。
(12)
求解得,当β=25.9°,α=48.5°时,min(L)=13 m。
则交织区需满足的最短距离为
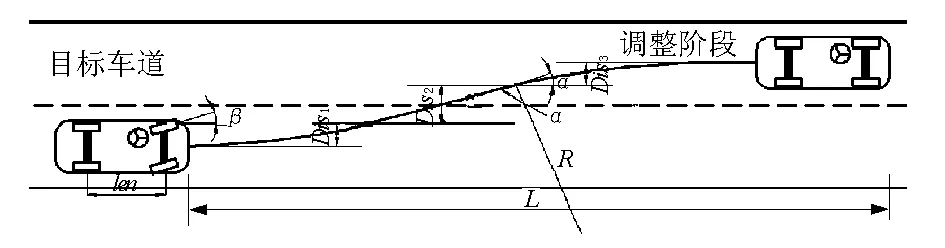
图3 交织车辆换道示意图
3.2仿真求解交织车道通行能力

步骤1。采集建模时所需的输入数据(有交织区的长度、车道的宽度、流量OD、自由流车速)及验证数据(本文采用交织速度与直行车速作为验证指标)。
步骤2。根据实际交织区的几何数据、驾驶行为数据、仿真控制参数等建立仿真基础模型。
步骤3。确定模型的精度要求(一般要求为仿真数据与实际观测数据偏差不大于10%),对仿真模型进行标定[11],标定过程见图4。
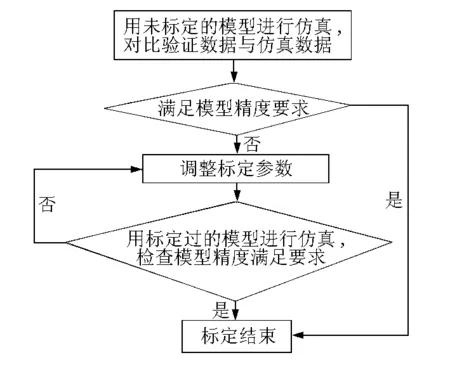
图4 模型标定过程
步骤4。重新构建仿真模型中的路网(交织区只包括分流车道和交织车道的路网)。
步骤5。确定上下匝道流量的交织比,以该比例作为上下匝道流量输入的依据,利用VISSIM中流量的多周期输入功能,逐步提高仿真输入流量,当系统的交通流出现溢出现象,这时系统(交织车道)所能通过的最大流量就作为交织车道的实际通行能力。
3.3可行性验证
由前文可知,直行车流的供需矛盾可通过增加直行车道来解决,故通过增加车道来改善交织区拥堵的可行性研究主要在于验证增设分流车道是否可以缓解交织车流的供需矛盾,验证流程见图5。
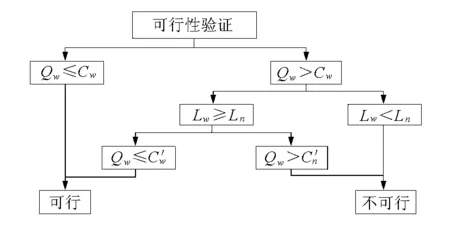
图5 可行性验证流程
3.4分流车道增设原则
4 案例分析
乌鲁木齐市广汇立交东西向南侧交织区改造前为3车道,高峰时段拥堵严重,见图6a)。其中上匝道交织流量为936 pcu/h,下匝道交织流量为1 020 pcu/h,直行流量总计为1 865 pcu/h(较交织流量小,且小于2个直行车道的通行能力),故引起拥堵的主因为交织车流的供需矛盾。该交织区长度为98 m,满足加宽时最小长度要求,由于上下匝道交织流量均较大,故在原车道两侧分别增设一条分流车道。按照上述流程,采用VISSIM仿真来求解加宽后交织区的通行能力,求解结果为2 950 pcu/h,大于交织需求,则增设分流车道可缓解交织区拥堵。
实际改造中为降低对主线交通的影响,将该交织区改建为“主线+集散车道”的组合(集散车道为4车道,主线为3车道),其中集散车道的流量为上匝道交织流量为936 pcu/h,下匝道交织流量为1 020 pcu/h,直行流量总计为817 pcu/h。考虑到建设成本及直行流量较小,且分流车道通行能力有剩余,未单独建设直行车道,而是让直行车流借用分流车道通行。目前,改造已经完成,高峰时段运行井然有序,见图6b)。

a)改造前b)改造后
图6交织区的运行状况
5 结语
由于直行车流的供需矛盾通过增设直行车道可以得到解决,故通过增加车道来改善交织区拥堵的可行性研究的重点就成为研究是否可通过增设分流车道来提高交织车道的通行能力,缓解交织车流的供需矛盾。研究的关键在于确定分流车道发挥作用时,交织区需满足的长度要求,以及增设分流车道后交织车道的通行能力;根据交织车辆的换道特征,提出交织区需满足的最短长度为26 m,采用VISSIM仿真软件对交织车道的通行能力进行了求解。本文的研究对象是已建成的拥堵交织区,但在设计阶段由于用地限制使得交织段的长度无法满足规范要求时,也可研究是否可以通过增加交织区车道的方法来提高交织区通行能力来满足直行车流与交织车流的通行要求。
参考文献
[1]LERTWORAWANICH PONLATHEP,ELEFTERIADOU LILY. Generalized capacity estimation model for weaving areas[J]. Journal of Transportation Engineering,2007(133):166-179.
[2]钟连德,荣建,孙小端,等.仿真求解快速路交织区通行能力[J].公路交通科技,2006(4):88-93.
[3]赵靖,白玉,杨晓光.基于回归分析的交织区通行能力模型[J].城市交通,2009(5):85-90.
[4]AWAD Wa’el H.Estimating traffic capacity for weaving segments using neural networks technique[J]. Applied Soft Computing,2004(4):395-404.
[5]Transportation Research Board. Highway capacity manual 2000[R]. Washington: Transportation Research Board Publications,2000:895-903.
[6]刘立英,李新刚,贾斌.基于元胞自动机模型的交织区通行能力特性研究分析[J].交通信息与安全,2013(3):28-32.
[7]ZHANG R H, Y. Analytical procedures for estimating capacity of freeway weaving, merge, and diverge sections[J]. Journal of Transportation engineering,2006,132(8):618-628.
[8]LI X G, GAO Z Y, JIA B. Capacity analysis of type-a weaving section by using cellular automata model[C].7th International Conference on Traffic and Transportation Studies, Kunming, China: Systems Engineering Society of China, Beijing Jiaotong University,2010:1011-1016.
[9]JIA B, LI X G, JIANG R, et al. Traffic behavior around the weaving section in cellular automata model[J]. International Journal of Modern Physics C,2010(3):409-422.
[10]吴娇蓉,辛飞飞.交通系统仿真及应用[M].上海:同济大学出版社,2012.
[11]荆彬彬,林培群,徐建闽.基于Vissim的3相交通流理论应用[J].交通信息与安全,2013(4):108-112.
收稿日期:2015-04-13
DOI 10.3963/j.issn.1671-7570.2015.04.046

