信用价差的度量模型及应用

邓华, 谭理



信用价差的度量模型及应用

邓华, 谭理

(湖南人文科技学院数学与计量经济系, 湖南娄底, 417000)

从衡量信用风险的主要工具信用价差的度量作为切入点, 分别利用期权定价和KMV理论建立了信用价差度量的2种模型, 并基于诸暨债数据, 实证评估了其信用价差。研究结果表明, 短期内KMV模型度量信用价差更合适, 长期这2种方法都趋近于真实数据, 模型可为理性的投资决策提供信息, 对刻画公司信用风险发挥积极作用。

信用价差; KMV模型; 期权定价理论

信用风险主要以信用利差作为衡量基准, 公司债券等信用债的大规模发行, 将有助于我国资本市场的多元化和层次化, 同时市场更加关注信用类品种的信用风险问题。本文将从信用价差的度量为切入点, 选取近些年债券相关数据为样本, 研究合理、有效的度量模型, 采用实证及定性定量相结合的分析模式, 从理论上研究信用价差的度量, 为信用利差刻画公司信用风险发挥积极辅助作用。

1 由期权定价理论评估信用价差

公司债券或其他信用债券为了融资, 将高于无风险利率水平的风险收益率作为投资者的风险补偿。信用价差为债券风险收益率和无风险债券收益率的差[1], 常用来衡量公司违约的风险和评估公司的违约概率。本文将导出信用价差度量的几种模型, 为完善信用风险测评提供依据。

在期初时刻, 设某公司的资产总价值为A, 其融资贷款额用表示, 时间期限跨度设为-, 借款到期日时刻的贷款本息之和为, 期末公司的价值为E。那么, 如果当到期时刻公司的价值低于此项贷款的到期偿还本息和时, 该公司就存在违约的可能。假定借款的预期收益率是, 市场无风险利率(连续复利)为, 则信用价差为=-。

信用价差与无风险利率成反方向变动, 与预期收益率同方向变动。即相同预期收益水平下, 随着无风险利率的增加, 信用价差下降, 信用风险减小。相同无风险利率水平下, 随着预期收益率越高, 贷款的信用风险越大。当前时刻贷款的本金为

=e(T – t)。 (1)

贷款银行在借给公司金额的同时, 为了规避风险, 再购买一份期权做套期保值, 该期权可看成是在期限-, 以融资公司资产作为标的物, 到期时贷款的本息和作为执行价格的欧式看跌期权。在期末时刻, 如果公司的总资产价值高于, 银行可以得到公司归还的贷款; 如果公司的价值低于或等于, 银行接管公司得到的公司期末价值为E, 再执行欧式看跌期权得到价差-E, 则不论发生何种情况, 银行都能获得无风险总收益。具体分析如下:

采用无套利定价法[2], 投资者可构建一份欧式看跌期权加上一笔数额为的贷款组合(图1)。

图1 期权定价法的组合价值分解图

若以无风险利率作为贴现率, 则贷款的本金、期末贷款本息的现值与期权价格0之间的关系为+0=e–r(T – t), 即0=e–r(T – t)-=(e–r(T – t)-e–y(T – t)), 而欧式看跌期权的价格可用Black – Scholes公式[3]表示为0=-(-1)A+e–r(T – t)(-2), 其中:

从式(2)可知, 信用价差仅取决于公司的资产价值波动率、借贷的时间期限跨度、市场的无风险利率水平等变量, 而与投资者的风险偏好无关。

2 由KMV模型度量信用价差

考察某家上市公司向银行融资借贷元, 借款期限为-。如果市场的无风险利率为, 银行给公司的贷款利率为, 到期时应还款的总额为, 期初公司签约时的资产价值用A表示, 预期公司的违约率为d, 预期公司的违约损失为, 可将价值按如图2进行分解。

(1) 如果融资到期日公司资产的价值大于应偿还的贷款本息和, 公司会选择偿还债务, 即履约概率为(1-d);

(2) 如果到期日公司资产的价值小于应偿还的贷款本息和, 公司资不抵债将无力偿还, 就会选择违约, 即违约的概率为d, 债权人银行仅能获得(–)元。用表示违约总额百分比, 则(–) =。

图2 KMV法的价值分解图

根据风险中性定价原理, 组合期末预期收益应等于期初贷款金额的终值, 否则会存在套利机会。即

e(T – t)=(1-d) +d(-), (3)

又因=e, 由式(3)有e-y(T – t)e(T – t)=(1-d) +d(–), 即

e(r – y)(T – t)= 1-d/, (4)

式(4)两边取以e为底的对数, 即可得银行贷款的信用价差[4]

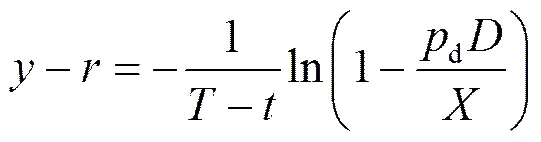
从(5)式可知, 信用价差可以由公司违约时的预期损失、预期概率、借贷期限和贷款总额等变量决定。

3 参数估计

3.1 估计漂移率及波动率

3.2 估计违约距离D

用违约距离D表示公司期末资产的价值与违约点间的差额,D的值愈大表明公司资产的价值愈高于违约点, 公司违约的概率越小, 反之, 值越小表明公司违约的可能性越大。其中违约距离[4]为

3.3 估计预期违约率d

假设公司的市场价值满足以平均市场价值为均值的正态分布, 当违约距离D< 0时, 公司就会选择违约, 即有[5]

值得注意的是此处的预期违约概率是“风险中性”的, 由于一般系统性风险都大于0, 所以≥。

4 数据处理

选诸暨债2011–12–30至2013–6–25日数据,= 1 522 063.77,A= 1 500 000,= 0.051 4,= 0.069 2,= 922 063.8, Shibor基准利率为本期债券发行首日前5个工作日全国银行间同业拆借中心在上海银行间同业拆放利率网(www.Shibor.org)上公布的1年期上海银行间同业拆放利率的5.14%。数据分别来自于方正证券和上海银行间同业拆放利率网站。数据分析结果分别见表1、表2及图3。

表1 期权定价模型

表2 KMV模型

图3 期权定价模型和KMV模型对信用价差的估计

由图3可知, 随着期限的增长, 不论是哪种模型, 其结果都有收敛于实际信用利差的趋势。但相比较而言, KMV拟合得更好, 值得注意的是KMV模型中d的选择非常关键, 若选取不当, 其拟合度比期权法要差。

5 结论

本文分别利用期权定价模型和KMV模型为信用价差定价, 通过真实数据对比分析了信用价差的度量, 本文定性、定量、数形结合分析了信用价差。从模型建立来看, 信用价差与投资者风险偏好及预期收益率无关, 只与公司资产价值的波动率、到期期限和无风险利率有关, 从数据结果来看, 短期内KMV模型相较期权定价模型更合适, 长期这2种方法都趋近于真实数据。

由于信用价差是衡量信用风险的一个重要工具, 因此本文的研究对增强投资者风险意识有帮助, 有利于投资者判断公司债券价格的合理性, 也有助于投资的理性决策, 同时对地方政府是否应采取“救市”的决策有一定指导意义。

参考文献：

[1] 程鹏, 吴冲锋, 李为冰. 信用风险度量和管理方法研究[J]. 管理工程学报, 2002, 16(1): 70–73.

[2] 郑振龙. 金融工程[M]. 北京: 高等教育出版社, 2008: 16–18.

[3] 约翰·赫尔, 著. 期权, 期货和其它衍生产品[M]. 张陶伟, 译. 北京: 华夏出版社, 2000: 211–221.

[4] 邓华. 期权定价原理在违约风险信用价差中的应用研究[D]. 长沙: 中南大学, 2006.

[5] 赵跃琼, 严广乐. KMV模型在银行贷款定价中的应用[J]. 上海理工大学学报, 2006, 28(1): 23–26.

(责任编校: 江河)

The measurement model of credit spreads and its application

Deng Hua, Tan Li

(Department of Mathematics and Econometrics, Hunan Institute of Humanities, Science and Technology, Loudi 417000, China)

Taking the evaluation of credit spreads as a breakthrough point which is the main content for assessment of credit risk, two measure models are built by Option Pricing Theory and KMV theory respectively, credit spreads of Zhuji debt are studied based on its actual data. The results show that the KMV model to measure the credit spread is more appropriate in short-term. But in the long term these two methods are both close to the real data. These models provide the essential information to make the right investment decisions and played positive effects for the evaluation of credit risk.

credit spread; KMV Model; option pricing theory

10.3969/j.issn.1672–6146.2015.02.012

F 224

1672–6146(2015)02–0035–04

邓华, huakate@163.com。

2014-10-30

湖南人文科技学院教学改革重点项目(RKJGZ1315)。