基于Voronoi图的奥林匹克森林公园风景游憩林空间结构分析

朱俐娜，彭祚登，俞琳锋

(北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083)

基于Voronoi图的奥林匹克森林公园风景游憩林空间结构分析

朱俐娜，彭祚登，俞琳锋

(北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083)

探究林匹克森林公园的林木竞争指数的空间格局，为合理经营森林提供依据。利用GIS的Voronoi图空间分析功能，确定空间结构单元；运用地统计学分析了林木竞争指数分布的空间变异特征，计算了竞争指数的变异函数，并用Kriging方法对竞争指数进行了插值。结果表明：在试验区内，林分存在7种空间结构单元，其中以1株对象木和5株最近邻木的空间结构单元最为常见；竞争指数的半方差函数可拟合成线性模型，呈随机分布；竞争指数的空间异质性较大。建议采取间伐和补植措施，以优化林分空间结构。

竞争指数；地统计学；Voronoi图；空间分布格局图；奥林匹克森林公园

竞争，是指两个或多个植物体对同一环境资源和能量的争夺中所发生的相互作用[1]。竞争指数反映的林木所承受的竞争压力，取决于林木本身的状态(如胸径、树高、冠幅等)和林木所处的局部环境(邻近树木的状态)。研究林木间的竞争关系，选择合适的指数十分重要，不同的竞争指数具有不同的生态意义和功能[2]。研究林木个体之间的竞争是研究森林生态系统的基础，同时林木个体的特点又是确定营林措施的重要基础[3]。

地统计学主要是以区域化变量理论为基础，可以定量描述生命有机体(个体、种群和群落)在同环境中的空间相关性和依赖性；还可以利用半变异函数结合样点的空间位置和方向，对样点中稀疏的或无规律的数据进行最优估值，有利于深刻了解生命有机体的空间分布情况和空间异质的机制[4-5]。目前，地统计学广泛应用于病虫害的空间格局[6]、土壤养分空间格局[7]、生物量估计[8]。

空间变异的最小尺度来源于林木自身属性的变异，竞争是林木个体最重要的属性之一，影响着林木个体的其他属性[9]。对于使用地统计学方法对平原地区林木竞争的空间格局和变异的分析，目前还未见报道。笔者以奥林匹克森林公园为试验地，采用地统计学方法定量地分析平原地区林木的竞争指数的空间分布结构特点，为今后城市森林营造提供指导。

1 试验地概况

试验地位于北京市奥林匹克森林公园(以下简称“奥森公园”)。奥森公园是目前北京市规划建设中最大的城市公园，分为南园和北园，占地面积分别为380hm2和300hm2。在整个奥森公园区域，多种乡土植物及群落构成主要的景观体，植被覆盖率达90％(植物群落区域占地面积高于70％)[10]。

试验样地选在奥森公园的北园，乔木主要有油松Pinus tabulaeformis、圆柏Sabina chinensis、杜仲Eucommia ulmoides、银杏Ginkgo biloba、臭椿 Ailanthus altissima、白 蜡 Fraxinus chinensis、国槐Sophora japonica、旱柳Salix matsudana等；灌木主要有金银木Lonicera maackii、三裂绣线菊Spiraea trilobata等；草本主要有紫花地丁Viola philippica、抱茎苦荬菜Ixeris sonchifolia、旋覆花Inula japonica、诸葛菜Orychophragmus violaceus等。

2 研究方法

2.1 调查方法

设置50m×50m样地，将样地内的林木进行编号，调查每株林木(胸径超过2cm)的胸径、树高、枝下高、冠幅，并利用超声波测距仪(Vertex IV，Sweden)测定其相对坐标(x,y)。

2.2 分析方法

2.2.1 竞争指数

竞争指标通常分为两种，一种与距离有关，一种与距离无关。按照合理性和可行性原则，通常选择与距离有关的竞争指数定量描述林木竞争情况[11]。目前，单木竞争指数的研究较多，提出了许多模型，但以Hegyi提出的单木竞争指数模型的预测效果最好[12]，因此本研究采用Hegyi竞争指数模型来计算竞争指数，其计算公式为[13]：

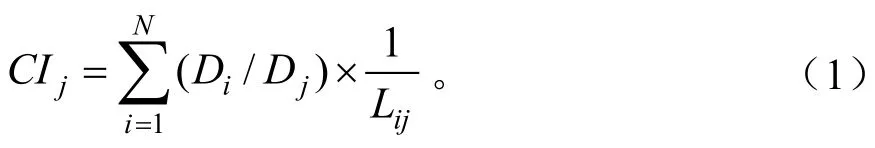
式中，CIj为对象木j的竞争指数；Di为相邻木i的胸径，Dj为对象木j的胸径；Lij为相邻木i和对象木j的距离；N为相邻木的株树。

把样地内的每株树木视为平面上的一个点，根据每株林木的坐标，借助ArcGIS 10.2中的Create Thiessen Polygons工具，创建样地的Voronoi图(图1)，将与对象木直接相邻的Voronoi多边形内的单木界定为最近邻木，以此确定林分空间结构单元[14]。根据Voronoi图的特点，每个多边形内仅包含1株林木，因此对象木的最近邻木株数与Voronoi图中相对应多边形的数目相等[15]。

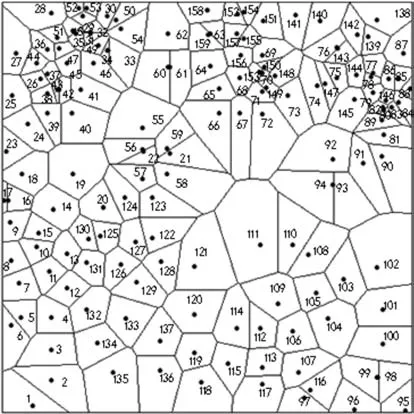
图1 由试验区内对象木构建Voronoi图Fig.1 Voronoi diagram and Delaunay triangulated network of target tree from experimental areas

为了减小边缘效应，本文采用距离缓冲区法进行边缘矫正，样地缓冲距离为2m[16]。本试验中，样地范围内共有159株林木，除去周边25株林木，对象木共134株。

2.2.2 地统计学方法

(1)半方差函数

半方差函数是指区域化变量Z(xi)和Z(xi+h)的增量平方的数学期望。其公式如下：

式中，γ(h)为半方差函数值，N(h)是被h分割的数据对(xi，xi+h)的对数，Z(xi)和Z(xi+h)分别是在点xi和xi+h处样本的测量值，h是两分隔样点的距离。

变异曲线图有3个重要参数，分别为块金值C0、基台值C0+C和变程A，它们决定半变异函数的形状结构[17]。块金值是指变异函数曲线被延伸到间隔距离为零时的截距，它反映了小于抽样尺度的随机变异和测量误差；基台值是指达到平衡时的变异函数值，它反映了空间异质性程度；变程是当变异函数的值达到平衡时的间隔距离，它反映了在某种观测尺度下空间相关性的作用范围[18]。

(2)变异函数理论模型的拟合

地统计学是用来拟合实际变异曲线图的理论模型，有线性模型、球状模型、指数模型和高斯模型等[19]。除线性模型表示竞争指数呈随机或均匀分布外，其余均表示呈聚集分布。在选择何种理论模型进行拟合的过程中，需要依次考虑决定系数R2、残差RSS、变程A和块金值C0的大小，以此来判断不同的理论模型在拟合实际变异曲线图时的优劣程度。本研究使用GS+9.0软件对竞争指数的空间格局进行地统计学分析。

(3)空间分布图的生成

Kriging法是一种对估计观测样点间内插值的地统计学方法，是由以xi为中心块段的平均值影响范围内的n个有效样本值Z(xi)的线性组合得到，其公式如下：

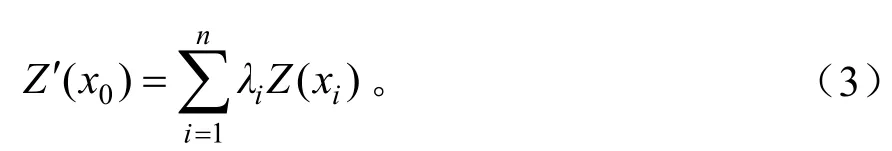
式中，Z′(xi)为待估点的值，λi是与样点观察Z(xi)有关的加权系数，用来表示各个样点Z(xi)对Z′(xi)的贡献。

当获得某个变量的半变异函数的拟合模型后，可对研究区域上未取得样点的区域化变量进行最小误差估计[6]。在surfer 8软件中借助Kriging插值法进行插值分析，并生成竞争指数的空间分布图。

3 结果与分析

3.1 林分空间结构单元

基于Voronoi图确定林分的空间结构单元，结果表明：对象木的最近邻木株数范围为3～9株，有7种可能取值(图2)。参照木的平均最近邻木数为5.42株，其中超过58.54％ 的参照木的最近邻木为5～6株。由此可知，该样地存在7种不同大小的空间结构单元，以1株对象木和5株最近邻木的构成形式最为常见。

3.2 竞争指数的半方差函数分析

根据已经得出的每株林木的空间结构单元，利用式(1)计算得到每株林木的竞争指数(表1)。

数据正态分布是半方差函数分析的前提[20]，采用Kolmogorov-Smirnov检验，发现样地的竞争指数不呈正态分布，所以本研究对竞争指数均采取了对数变换，使之符合正态分布。

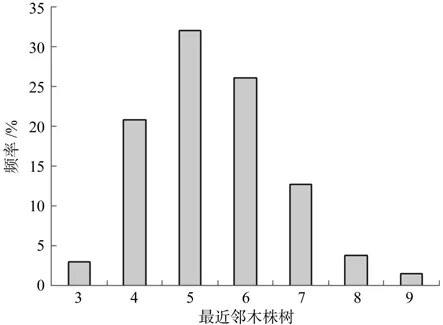
图2 对象木的最近邻木株数频率分布Fig.2 Frequency distribution of the number of nearest neighbor trees around the target tree

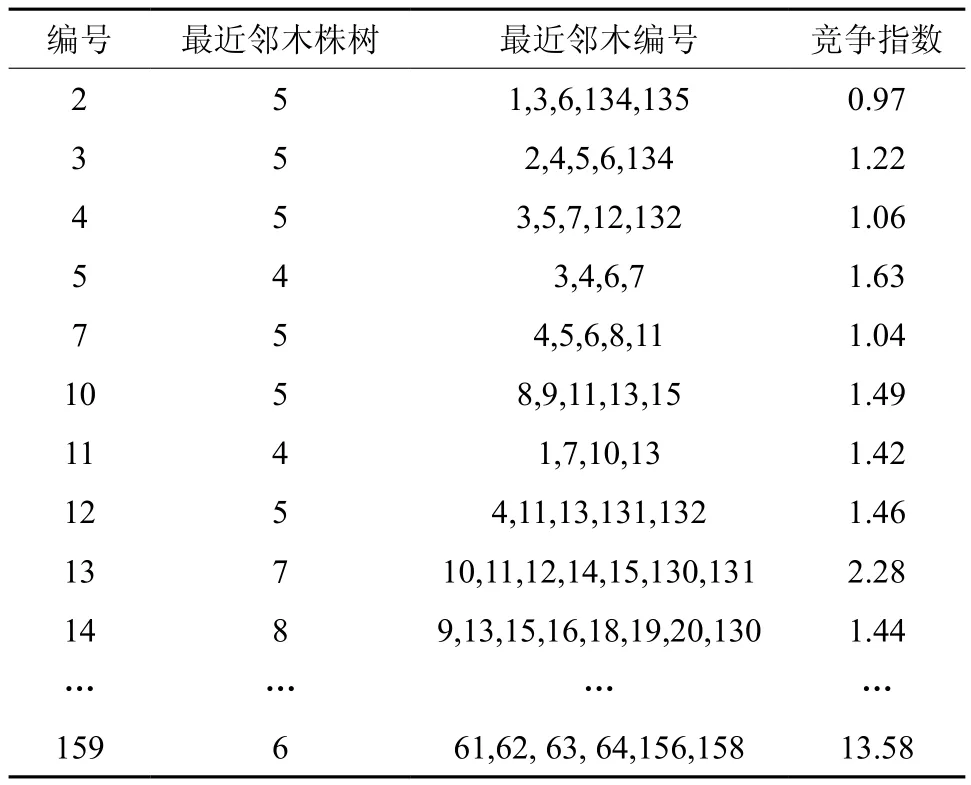
表1 基于Voronoi图的竞争指数计算结果Table 1 The calculation results of spatial structure indexes based on Voronoi diagram triangulated network

竞争指数的半方差函数模型反映了竞争指数的分布状态。从整体上看，样地竞争指数的半方差函数模型与线性模型拟合最好，决定系数达0.689，竞争指数呈随机分布；其空间依赖范围为28.563m，即在此距离范围之内的任何两样点竞争指数间都存在着一定的相关关系(见表2)。样地南侧和样地北侧分别拟合成指数模型和球形模型，均呈聚集分布，但前者的决定系数仅0.457，而后者达0.741，说明样地南侧的指数模型拟合效果较差(见表2)。

结构比表明由空间自相关引起的空间异质性程度，当该比值≤25％时变量空间自相关程度为微弱，比值为25％～75％时变量空间自相关程度为中等，比值≥75％时变量空间自相关程度为强烈[20]。从整体上看，结构比为29.6％，处于25％～75％，表现出中等程度的空间自相关，而样地南侧和样地北侧的空间变异比分别达99.9％和87.2％，高于75％，两者表现出很强的空间自相关(表2)。

表2 竞争指数半方差函数的理论模型参数Table 2 Parameters of theory model in semi-variance function of competition index

3.3 竞争指数的空间分布格局图

为了更直观地了解竞争指数的分布特征，在所得变异函数指数模型的基础上，采用Kriging插值法绘制竞争指数空间分布格局图。由图3可知，竞争指数的空间异质性较强，在样地中呈明显变化。竞争指数由样地西南侧向北侧和东侧逐渐增大。竞争指数在北侧的异质性大于南侧。同时，在样地南侧，地势平坦，竞争指数较小；而在样地北侧，地势偏高，竞争指数较大。

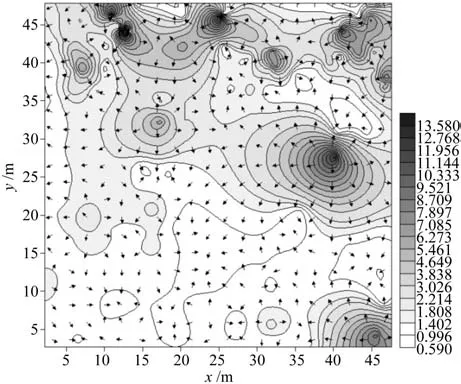
图3 竞争指数的空间分布格局图Fig.3 Space Distribution Patterns of competition index

4 结论与讨论

在试验区内，林分存在7种空间结构单元，其中以1株对象木和5株最近邻木的空间结构单元最为常见。汤孟平等、赵春燕等和汪平等基于Voronoi图确定的空间结构单元与本研究基本一致[14,15,21]，说明不同类型的林分可能存在相似的空间结构单元。利用Voronoi图确定林分空间结构，具有较强的灵活性、实用性和准确性，对今后的相关研究有重要意义。

由分析结果可知，半方差函数是分析竞争指数空间分布格局的强有力的方法。样地南侧和样地北侧均呈聚集分布，而从整体来看，竞争指数呈随机分布，出现这种情况的原因可能是样地南侧拟合的指数模型效果较差，其决定系数仅有0.457，同时，从图3可以看出，样地东南侧的竞争指数呈较明显的聚集分布，而样地南侧中部和西南侧的竞争指数的聚集性较弱。

样地南侧和样地北侧的竞争指数空间异质性大，对空间占据能力弱，竞争呈衰退趋势，有利于林木生长；而样地整体的竞争指数空间异质性较小，对空间占据能力较强，竞争态势稳定，不利于林分生长，建议进行林分抚育间伐，去掉劣势木，并调整林分密度，以保证保留木健康生长。

竞争指数在北侧的异质性大于南侧，主要是因为北侧树木的栽植距离多样，诸如圆柏等针叶树种栽植紧密，而杜仲等阔叶树种栽植稀疏。对于圆柏等针叶树种，其竞争指数大，密度大，存在较多的枯枝，建议对其进行抚育间伐，使株行距保持在1.5m×1.5m，以减小林分密度。而竞争指数在样地上坡(北侧)较大，在样地平面(南侧)较小，这可能是人工造林时，为了给游人提供更宽敞的游憩点，使得在平坦的南侧种植的树木较北侧少，栽植距离较大，建议以自由式组团的方式补植紫叶李、元宝枫等观赏树种，以进一步提升林分的美景度。

因为林木间的竞争除了受密度制约、自疏效应、大小等级等因素影响,还受到立地条件、小气候、林分密度、个体植株的大小、生长速率、发育阶段、个体生活力、生态习性、生态幅、生态位等因素的影响[22]，所以，在公园的林分经营管理中，需全面考虑各项因子，以保证林分健康生长。

[1] 惠刚盈,胡艳波,赵中华,等.基于交角的林木竞争指数[J].林业科学,2013,49(6)：68-73.

[2] 马履一,王希群.生长空间竞争指数及其在油松、侧柏种内竞争中的应用研究[J].生态科学,2006,25(5)：385-389.

[3] OLIVER C D,LARSON B C.Forest stand dynamics [M].New York：John Wiley &Sons Inc,1996.

[4] 张仁铎.空间变异理论及应用[M].北京：科学出版社,2005：13.

[5] 冯益明.空间统计学理论及其在林业中的应用[M].北京：中国林业出版社,2008：1-123.

[6] 章一巧,刘永华,宗世祥.基于GS+的大黄枯叶蛾卵的空间分布关系[J].林业科学,2013,2013,49(10)：100-105.

[7] 杜洪业,徐程扬,张添咏.阔叶红松林土壤养分空间异质性地统计学分析[J].东北林业大学学报,2013,41(10)：98-102.

[8] 贺 鹏,张会儒,雷相东.基于地统计学的森林地上生物量估计[J].林业科学,2013,49(5)：101-109.

[9] 周 隽,国庆喜.林木竞争指数空间格局的地统计学分析[J].东北林业大学学报,2007,35(9)：42-44.

[10] 潘剑彬.北京奥林匹克森林公园绿地生态效益研究[D].北京林业大学,2011.

[11] 汤孟平.森林空间结构研究现状与发展趋势[J].林业科学,2010,46(1)：117-122.

[12] 史 宇,余新晓,岳永杰,等.北京山区天然侧柏林种内竞争研究[J].北京林业大学学报,2008,30(S2)：36-40

[13] Radtke P J,Westfall J A,Burkhart H E.Conditioning a distancedependent competition index to indicate the onset of intertree competition[J].Forest Ecology and Management,2003,175(1/2/3)：17.

[14] 汤孟平,周国模,陈永刚,等.基于Voronoi图的天目山常绿阔叶林混交度[J].林业科学,2009,45(6)：1-5.

[15] 赵春燕,李际平,李建军.基于Voronoi图和Delaunay三角网的林分空间结构量化分析[J].林业科学,2010,46(6)：78-84.

[16] 周红敏,惠刚盈,赵中华,等.林分空间结构分析中样地边界木的处理方法[J],林业科学,2009,45(2)：1-5.

[17] 王晓春,韩士杰,邹春静,等.长白山岳桦种群格局的地统计学分析[J].应用生态学报.2002,13(7)：781-784.

[18] 甘静静,曾思齐,肖化顺,等.木荷次生林地土壤养分空间异质性研究[J].中南林业科技大学学报.2014,34(5)：9-16.

[19] 赵 军,刘焕军,隋跃宇,等.农田黑土有机质和速效氮磷不同尺度空间异质性分析[J].水土保持学报,2006,20(1)：41-45.

[20] 杨子清,陈平留,刘 健,等.基于Kriging法的森林土壤养分空间插值[J].福建农林大学学报(自然科学版),2012,41(3)：296-300.

[21] 汪 平,贾黎明,魏松坡,等.基于Voronoi 图的侧柏游憩林空间结构分析[J],北京林业大学,2013,35(2)：39-44.

[22] 陶 岩,殷秀琴,田育红,等.长白山红松针阔混交林种内、种间竞争关系研究[J].北京师范大学学报(自然科学版),2011,47(4)：428-431.

Analysis of spatial structure of scenic and recreational forest of olympic forest park based on Voronoi

ZHU Li-na,PENG Zuo-deng,YU Lin-feng
(Key Laboratory for Silviculture and Conservation of Ministry of Education,Beijing Forestry University,Beijing 100083,China)

To explore the spatial pattern of competition index in forests of Olympic Forest Park and provide evidences for reasonable management forest.Spatial structure unit was established with Voronoi diagram spatial analysis function of GIS.An experiment was conducted to study the spatial pattern of competition index in forests by the geostatistics.Sem ivariogram and Kriging map of competition index were calculated.Results indicate that there are 9 kinds of spatial structural units,in which 1 target tree with 5 nearest neighbor trees is the most common spatial structural unit.The sem ivariogram of competition index fi ts a linear model and exhibits a random spatia l aggregation.The competition index shows a higher spatial heterogeneity.Thinning and complementary planting measures can optimize stand spatial structure.

competition index; geostatistics; Voronoi diagram; spatial distribution pattern map; olympic forest park

S727.5

A

1673-923X(2015)07-0057-05

10.14067/j.cnki.1673-923x.2015.07.011

2014-10-10

北京市科技计划项目“首都平原百万亩造林科技支撑工程”(Z121100008512002)；“应对PM2.5空气污染的北京造林工程关键技术研究与示范”(Z121100000312069)

朱俐娜，硕士研究生

彭祚登，副教授，博士；E-mail：zuodeng@sina.com

朱俐娜，彭祚登，俞琳锋.基于Voronoi图的奥林匹克森林公园风景游憩林空间结构分析[J].中南林业科技大学学报，2015,35(7)：57-61.

[本文编校：吴 毅]