基于状态转换动态Copula模型的外汇套期保值研究
唐韬,谢赤
(湖南大学工商管理学院,湖南长沙,410082)
基于状态转换动态Copula模型的外汇套期保值研究
唐韬,谢赤
(湖南大学工商管理学院,湖南长沙,410082)
汇改以来,人民币汇率波动的不确定性增大,外汇风险加剧,在此形势下加强外汇风险管理势在必行。考虑到利用外汇期货合约进行套期保值是管理外汇风险的一个重要方法,因此可建立一个状态转换动态Gaussian Copula套期保值模型来对外汇风险进行管理。首先采用GJR-t模型描述欧元、日元、英镑、澳元和加元的现货和期货收益率的边际分布;然后引入状态转换动态Copula函数描述上述五种货币的现货和期货收益率之间的相关性;最后将状态转换动态Gaussian Copula模型与OLS,DCC GARCH,DCC Gaussian Copula等模型的套期保值效率进行比较。实证结果表明,所构建的模型优于其他模型,利用该策略模型能有效规避外汇风险。
套期保值;汇率风险;状态转换;动态Copula模型
一、引言
科技日新月异,全球经济高速发展,金融自由化进程逐步深入,中国与各国经济的关联度越来越密切,与之相伴随的是国家之间的汇率等金融风险的增加。2005年以后,中国推行“以市场供求为基础、参考一揽子货币进行调节、有管理的浮动汇率制度”,外汇市场进一步开放,而深化金融改革也主要是围绕利率市场化以及汇率形成机制等内容。这在有利于我国经济未来发展的同时,也不可避免地加剧了企业、投资机构的外汇风险。另外,近年来次贷危机、国际金融危机、欧债危机相继爆发,发达国家汇率出现大幅波动,外汇市场起伏不定,给外汇风险起到了推波助澜的作用。
因此,外汇风险对投资者、涉外企业而言已是一种现实的存在,投资者要想获得收益,必须采取有效措施对外汇风险进行管理。以往,企业一般选取一些比较传统的外汇风险管理方法,例如选择有利的合同货币、合同中加列汇率条款、提前和推迟收付外币、压低采购价格、提高出口报价等。但这些方法的实施有着许多限制条件,相关方很可能无法达成一致,所以这些方法的效果并不理想。近些年,利用金融衍生工具来规避外汇风险被广泛应用,并取得一定成效,例如用外汇期货合约进行套期保值。Simpson和Dania[1],Lien[2],Chiang[3]等的研究都表明,利用外汇期货合约进行外汇套期保值是一种很好的规避外汇风险的策略。因此,本文拟利用外汇期货合约来考察并比较其管理外汇风险的效果。
二、文献综述
套期保值是指用买进或卖出期货合约的方式来规避现货价格波动带来的风险。为了最大程度地降低外汇风险,套期保值模型的科学性和精确性非常重要。
早期,一些学者采用GARCH类模型来探讨套期保值问题。谢赤等[4]用最小方差作为风险测度的指标,采用包含误差修正结构的GARCH模型探讨外汇期货的套期保值,实证结果表明该方法比传统方法有着更好的降低风险的能力。吴晓[5]运用BEKKGARCH模型,考察外汇套期保值策略,结果表明套期保值能有效减少汇率风险,但套期保值策略效率的高低与避险频率存在较大关联。彭红枫和叶永刚[6]运用一个修正的ECM-GARCH模型,分析在铜期货市场上进行的套期保值策略,结果显示相对于传统的ECM-GARCH模型,修正的ECM-GARCH模型套期保值效果要好。然而,以上文献在估计套期保值比率时大都假定资产收益率服从联合正态分布,而这一假设明显有悖于金融资产波动的异方差、偏峰以及厚尾等特性,所以存在较大的不合理性。Copula理论的发展为学者们提供了一种解决该问题的方法。Copula函数跳出了正态分布假设的束缚,可以将不同的边际分布结合成多元联合分布,更为有效地刻画金融数据的特性。
赵家敏和沈一[7]运用Copula模型,对韩国KOSPI200股指期货与现货间的套期保值比率进行了估计。王玉刚等[8]考察了基于Copula函数的铜现货的最优套期保值比率,并通过实证对比证明Copula模型套期保值策略有着优于传统套期保值模型的表现。马超群和王宝兵[9]运用Copula模型,分析了欧元和英镑期货合约的最优套期保值比率,实证结果显示Copula模型的套期保值效果优于CCC-GARCH和ECMGARCH模型。
不过,它们所采用的都是静态Copula函数,假定在样本期内期货和现货之间的相关性系数不变,这一点与现实是不相符的。实际经济活动中,期货和现货的相关性会因受到各种冲击而发生改变,所以上述学者所设定的模型在理论上仍存在较大误差。因此,为了更准确地得到最优套期保值比率,学者们开始将动态Copula函数运用于套期保值的研究中,动态Copula函数能有效刻画期货和现货之间的动态变化关系。
Lai和Chen[10]采取动态Copula模型对证券市场的套期保值效果进行了分析,认为动态Copula模型的套期保值效果好于传统静态模型。Wei等[11]运用动态Copula模型对沪深300进行套期保值,也得到同样的实证效果。史美景和赵永淦[12]构建了动态Copula-TGARCH模型研究套期保值,实证发现Copula-TGARCH模型的套期保值效果好于ECM-CCC-GARCH模型和ECM-DVEC-GARCH模型。周亮球和谢赤等[13,14]用时变Clayton-Copula模型和M-Copula模型探讨了外汇期货合约的套期保值问题和黄金市场最优套期保值比率问题。
从已有文献来看,动态Copula模型的建模效果普遍优于静态Copula模型。但美中不足的是,以往的动态Copula模型都没有考虑到金融市场或金融资产之间相关程度的状态转换特征,Rodriguez[15],Okimoto[16]以及Garcia[17]认为,金融市场间的相关性程度会随着市场状态的不同而改变,在高波动和低波动段它们之间呈现不同的相关结构,把握这种相关程度状态转换特性对金融风险管理至关重要。谢赤等[18]用状态转换Copula模型对股指期货套期保值问题进行了深入分析,实证结果表明,引入状态转换机制后,套期保值效果要优于普通的动态Copula模型。另外,以往有关外汇套期保值的文献所选择的货币品种单一,而实际经济活动中,投资者、涉外企业往往需要对多种外币进行套期保值以规避风险。因此,本文拟选择国际上常用的5种外汇期货合约,根据数据的特性,建立一个马尔可夫状态转换动态Copula(Markov regime switching dynamic Copula, MRSD-Copula)模型来对外汇套期保值问题进行研究,为相关主体的外汇风险管理提供新的思路。
三、模型构建
Copula是指将多元联合分布与其一维边际分布联系起来的函数。根据Copula函数的相关原理,本文运用两阶段法构建状态转换动态Copula模型:首先决定边际分布,然后设定Copula函数。
(一) 边际分布模型的设定
边际分布的选取是十分重要的,其合理与否将会在很大程度上影响套期保值模型的模拟效果。以往研究表明,金融收益率往往存在自相关及条件异方差,以及尖峰、厚尾、杠杆效应等特性,因此,本文采用AR(p)-GJR-GARCH模型对各货币的收益率进行建模,同时设定误差形式服从t分布。
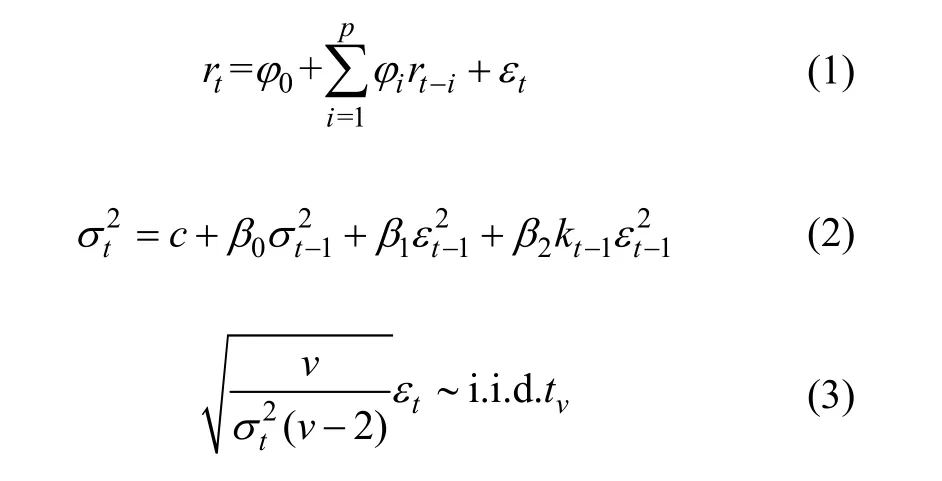
其中:rt表示t时刻的收益率,φ0为一个截距项,φi表示滞后i期的收益率对当期的影响,εt为一个残差项;σt表示t时刻收益率的条件波动率,c1,β0,β1,β2为需要估计出的参数,它们都大于零,β0+β1+0.5β2的大小反映了收益率波动的持续效果,β2用来衡量“杠杆效应”,反映上一期利空或利好消息对当期收益率波动的影响;kt−1作为式子中的虚拟变量,如果残差项εt−1为负时,kt−1为1;反之如果残差项εt−1为正时,kt−1为0。(3)式中的v为自由度。
(二) 状态转换动态Copula函数的设定
近年来,Copula函数越来越多地被应用于金融研究领域。对于收益率相关关系的刻画,学术界大多使用Gaussian Copula函数和t Copula函数。Hsu[19],Lai[20]等的研究表明,Gaussian Copula函数能取得较好的套期保值效果,因此本文选用它来进行实证研究。Gaussian Copula的条件密度函数为:

其中:Φ−1(·)是标准正态分布函数Φ−1(·)的逆函数,ρ为相关性系数。
Rodriguez[5],Okimoto[16]以及Garcia[17]研究表明,金融市场间的相关程度存在状态转换特征,因此本文令Gaussian Copula中的相关参数服从2阶段Markov状态转换过程。定义转换概率为:

令p11=p,p22=q,则2状态的Markov转换概率矩阵可以表示为:

那么,在时刻t,Markov状态转换Gaussian Copula函数可表示如下:

同时,考虑到传统的Markov状态转换Copula函数没有考虑高波动和低波动状态下金融资产间相依结构的动态改变,因此为突出建模的精确性,本文再参考Tse和Tsui[21]的研究,设定Markov状态转换Gaussian Copula函数中的相关性ρ参数服从如下过程:

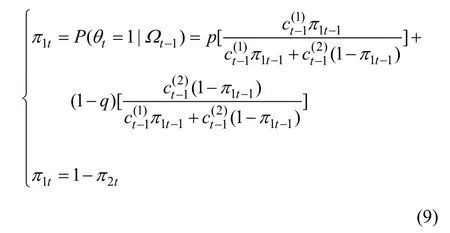
(三) 模型的参数估计
令边际分布的参数集合为θi,状态转换动态Copula函数的参数集合为θc,本文采用Patton提出的两阶段极大似然法来估计Copula模型的参数[12]。
第一步,对各收益率序列的边际分布参数θi进行最大似然估计:

第二步,得到上面的边际分布参数后,将其代入到状态转换动态Copula函数中,利用数值方法估计出Copula函数的参数:

四、实证研究
(一) 数据来源及处理
2006年8月28日,芝加哥商品交易所(CME)曾经推出人民币期货合约,但由于那时投资者只持有多头,而空头需求缺很少,所以限制了期货的成功。2011年10月17日,CME又上市新人民币期货合约USD/ RMB,但由于人民币在国际上缺乏流通性,所以成交量非常少,且这些合约不具备连续性,无法得到其准确数据。同时,还考虑到目前期货市场上没有人民币兑日元、欧元、加元、英镑、澳元的期货合约,另外美元在国际上占据着主导流通地位,因此本文选取美元(USD)为本币,选取日元(JPY)、欧元(EUR)、加元(CAD)、英镑(GBP)和澳元(AUD)的期货合约研究外汇套期保值问题。考察的时间段为2008年1月1日至2014年7月1日,删除掉期货市场与现货市场不在一天的数据,共筛选出1925个样本值。
外汇期货数据来源于华尔街日报(http://asia.wsj. com/home-page),外汇现货数据来源于美国联邦储备委员会网站(http://www.federalreserve.gov/),所有汇率数据均采取直接标价法进行表示。为避免交易量稀薄以及到期日临近时价格发生异动对真实结果所造成的偏差,与以往研究一致,本文选择最近到期日的合约,但不选择交割月份的合约。具体为,上一年12月份和本年1月、2月份选择本年3月份的合约,本年3月、4月、5月份选择本年6月份的合约,本年6月、7月、8月份选择本年9月份的合约,本年9月、10月、11月份选择本年12月份的合约,按照此原理,构造出连续的货币期货价格序列。
通过对原汇率序列进行一阶对数差分并乘以100得到现货和期货的收益率序列。即:

(二) 数据分析
对各货币收益率序列做统计分析,结果如表1。

表1 各货币现货和期货收益率的描述性统计
从表1可知,不论何种货币,其现货和期货收益率基本一样,日元和澳元的收益率均为正值,而英镑、欧元和加元的收益率都为负值,这与近年来外汇市场的实际情况相吻合。标准差反映市场的平均波动水平,而澳元的波动程度最高,但是其他市场的波动大小相差不大。各货币现货与期货之间的标准差差别不显著,表明二者的波动情况大体相同,这与实际金融活动中,现货与期货价格变化趋势大致相同。各种货币收益率在峰度上显著大于3。同时,从Jarque-Bera统计量来看,所有收益率序列均在1%显著水平上显著,拒绝正态分布的原假设,表明各个收益率的序列表现出尖峰厚尾特性。而各货币在偏度上均表现出不同程度的左偏或右偏。此外,条件异方差检验表明,各种货币的收益率都存在高阶ARCH效应,所以可用GARCH模型建模。
本文采用ADF和PP检验对各货币收益率序列进行单位根检验,考察是否有“伪回归”现场出现,检验结果如表2。

表2 各货币收益率单位根检验
由表2知,所有收益率序列ADF检验和PP检验统计量在1%的置信水平上都显著,表明各货币收益率序列是平稳的,可进行下一步实证分析。
(三) 参数估计
边际分布的合理与否对套期保值效果的优劣具有重要影响,本文采用AR(p)-GJR-t模型对各货币现货和期货收益率的边际分布做拟合,模型参数通过估算,结果如表3。

表3 边际分布的参数估计
从ARCH-LM检验结果可以看出,原本各收益率存在的ARCH效应已消除。其中β0+β1+0.5β2的值接近于1,说明各收益率序列波动效应持续久。对于欧元期货收益率,杠杆效应β2的t统计值即使在10%的水平上仍不显著,表明投资者对利空和利好消息反映差异不大,而对于其他收益率序列,t统计值在10%置信水平上均显著,表明存在杠杆效应。其中,日元β2的值为负,英镑、澳元和加元β2的值为正,表明日元存在正向杠杆效应,投资者对利好消息反映强烈,英镑、澳元和加元存在负向杠杆效应,投资者对利空消息反映强烈。在确定各汇率收益序列的边际分布后,对其进行K-S检验,各序列在1%水平上均通过检验,说明本文对边际分布的拟合是合理的,可以进行下一步工作。
根据边际分布的参数估计结果,得到各货币的累积分布函数值序列u以及序列v,通过它们对状态转换动态Gaussian Copula函数进行参数估计,所得结果如表4。

表4 状态转换动态Gaussian Copula函数参数估计
(四) 套期保值比率的估计及效果比较
最优套期保值比率为风险最低的情况下,期货与现货持有头存之比,通常用h表示,具体公式为:

这是一种静态的套期保值比率。但在实际经济活动中,资产间的联合分布往往呈现时变的特性,因此上式所求得的套期保值比率不够准确。目前,较为理想的套期保值比率计算方法为:令st表示时刻t现货价格的变化,ft表示t时刻期货价格的变化,最小化套期保值的组合收益(st−ht−1ft)的方差获得最优时变套期保值比率,其公式为:
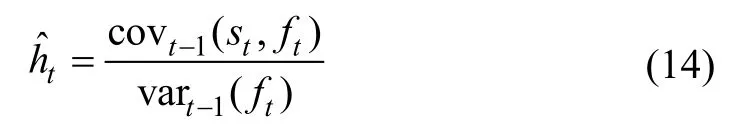
由上式可知,要想得到最优套期保值比率,首先要估计联合密度函数。在前面,我们已经介绍两阶段的极大似然法估计边际分布及Copula函数,通过函数参数估计,得到时变的联合密度函数,再进一步求解得到期货与现货收益率之间的协方差:

其中:σsf,t为期货和现货收益率的协方差,为现货和期货收益率的条件联合分布密度;σs,t和σf,t分别为时刻t现货和期货收益率的条件波动率。最后,将协方差序列以及求解的期货条件波动率,代入上式便得到最优套期保值比率h(见表5):


表5 最优套期保值比率h*的估计
从表5可以看出,各货币的最优套期保值比率的均值都小于1,集中在0.749 6至0.814 3之间,表明套期保值的头寸中,期货交易的数额应该少于现货。同时,由最优套期保值比率的最大值和最小值来看,这两个值差别较大,这表明了最优套期保值比率所存在的时变性。
为突出本文所构建模型的优越性,下面将状态转换动态Gaussian Copula模型与其他套期保值模型进行有效性对比。套期保值有效性指按某比例做套期保值时,比不做时的收益率风险降低程度,也是衡量套期保值比率优劣的标准。参考最新研究,本文以Hec为套期保值效率测度指标,其公式为:

式中:Hec是套期保值有效性,Var(Rp)表示做套期保值后的收益率的方差,Var(Rc)表示不做套期保值的收益率的方差。
本文的对比模型有传统的OLS模型、近年来运用较多的DCC GARCH模型和DCC Gaussian Copula模型。下面将对相关模型的套期保值有效性Hec进行计算,所得结果如表6。

表6 各模型套期保值有效性Hec比较
从表6可以看出,DCC GARCH、DCC Gaussian Copula以及MRSD Gaussian Copula所得到的套期保值有效性指标都比传统的OLS方法大,这体现了动态套期保值策略的优越性。同时,除英镑外,状态转换动态Gaussian Copula模型所得到的Hec都大于OLS,DCC GARCH,DCC Gaussian Copula套期保值策略得到的Hec,这体现了本文所构建模型的优势。同时,对于英镑,MRSD Gaussian Copula模型的套期保值效果不如DCC Gaussian Copula,这可能是因为DCC Gaussian Copula比MRSD Gaussian Copula能更好地描述英镑现货和期货间的相关性,但相比OLS方法,它的套期保值有效性仍有着显著提升,且它的Hec值与DCC Gaussian Copula的Hec值相差不大。所以,总体上说本文所构建的模型相比其他常用套期保值模型而言有着较显著的优势,意味着该策略模型能有效规避外汇风险。
五、结论
本文选取了英镑、欧元、澳元、加元、日元5种国际常用货币兑美元的期货合约考察外汇套期保值,以最小方差为风险测度指标,采用了较多数据,比较分析了状态转换动态Copula模型与其他套期保值模型的套期保值效果,研究结论和建议如下。
(1) 条件异方差、非正太、波动聚集特性在各货币的收益序列均体现得较为明显。同时,日元、英镑、澳元和加元还存在杠杠效应。其中,日元存在负向杠杆效应,英镑、澳元和加元存在正向杠杆效应。
(2) 各货币的现货和期货之间的相关性是时刻变化的,且存在状态转换的特性,状态转换动态Copula模型很好地刻画了这些特征,保证了模型的精确性。
(3) 从套期保值有效性来看,动态套期保值策略普遍优于静态套期保值策略。本文所构建的MRSD Copula模型在欧元、日元、澳元和加元市场上的套期保值有效性都优于现有的常用套期保值模型。仅仅对于英镑,DCC Gaussian Copula的套期保值有效性高于MRSD Gaussian Copula,但两者的差别也很小,这说明本研究更充分地刻画出了期货市场套期保值的规律,有关主体根据本文模型进行外汇套期保值可以有效规避汇率风险。
本文用外汇期货合约进行套期保值,而外汇风险管理还应根据情况选取合适的金融衍生工具,但要注意外汇衍生品所具有的风险性,要建立预警机制。同时,金融资产的收益率还可能存在比如跳跃或者结构突变等特性,因此下一步工作是全面考察金融资产收益率的这些特性,以期建立更有效的套期保值策略。
[1] Simpson W M, Dania A. Selectively hedging the Euro [J]. Journal of Multinational Financial Management, 2006, 16(1): 27−42.
[2] Chiang Y C, Liao L T, Hsiao A T. Evaluating hedging strategies in the foreign exchange market with the stochastic dominance approach [J]. Applied Financial Economics, 2011, 21(7): 493−503.
[3] Lien D, Yang L. Spot-futures spread, time-varying correlation, and hedging with currency futures [J]. Journal of Futures Markets, 2006, 26(10): 1019−1038.
[4] 谢赤, 刘薇, 吴晓. 关于外汇期货套期保值比率的实证研究[J]. 湘潭大学学报, 2005, 29(6): 103−106.
[5] 吴晓. 最优动态汇率风险套期保值模型研究[J]. 财经理论与实践, 2006, 27(144): 24−27.
[6] 彭红枫, 叶永刚. 基于修正的ECM-GARCH模型的动态最优套期保值比率估计及比较研究[J]. 中国管理科学, 2007, 15(5): 29−35.
[7] 赵家敏, 沈一. 股指期货最优套期保值比率——基于Copula-GARCH模型的实证研究[J]. 经济纵横, 2008, (5): 21−24.
[8] 王玉刚, 迟国泰, 杨万武. 基于copula的最小方差套期保值比率研究[J]. 系统工程理论与实践, 2009, 29(8): 1−10.
[9] 马超群, 王宝兵. 基于Copula-GARCH模型的外汇期货最优套期保值比率研究[J]. 统计与决策, 2011, (12): 124−128.
[10] Lai Y H, Chen Y S, Gerlach R. Optimal dynamic hedging via copula-threshold-GARCH models [J]. Mathematics and Computer in Simulation, 2009, 79(8), 2609−2624.
[11] Wei Y, Wang D Y, Huang D S. A copula-multifractal volatility hedging model for CSI300 index futures [J]. Physica A, 2011, 390(23): 4260−4272.
[12] 史美景, 赵永淦. 基于Copula-TGARCH模型的股指期货最佳套期保值比研究[J]. 数理统计与管理, 2012, 31(2): 354−362.
[13] 周亮球, 谢赤. 商业银行外汇套期保值研究——一个基于时变Clayton Copula-LPM模型的实证[J]. 南大商学评论, 2013, 10(4): 72−88.
[14] 谢赤, 屈敏, 王纲金. 基于M-Copula-GJR-VaR模型的黄金市场最优套期保值比率研究[J]. 管理科学, 2013, 26(2): 90−99.
[15] Rodriguez J C. Measuring financial contagion: A Copula approach [J]. Journal of Empirical Finance, 2007, 14(3): 401−423.
[16] Okimoto T. New evidences of asymmetric dependence structures in international equity markets [J]. Journal of Financial and Quantitative Analysis, 2008, 43(3): 787−816.
[17] Garcia R, Tsafack G. Dependence structure and extreme comovements in international equity and bond markets [J]. Journal of Banking and Finance, 2011, 35(8): 1954−1970.
[18] 谢赤, 余聪, 罗长青, 王纲金. 基于MRS Copula-GJRSkewed-t模型的股指期货套期保值研究[J]. 系统工程学报, 2013, 28(1): 83−93.
[19] Hsu C C, Tseng C P, Wang Y H. Dynamic hedging with futures: a copula-based garch model [J]. The Journal of Futures Markets, 2008, 28(11): 1095−1116.
[20] Lai Y H, Chen Y S, Gerlach R. Optimal dynamic hedging via copula-threshold-GARCH models [J]. Mathematics and Computers in Simulation, 2009, 79(8): 2609−2624.
[21] Tse Y K, Tsui A K C. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations [J]. Journal of Business and Economics Statistics, 2002, 20(3): 351−362.
[22] Gray S F. Modeling the conditional distribution of interest rates as a regime-switching process [J]. Journal of Financial Economics, 1996, 42(1): 27−62.
Hedging foreign exchange through regime-switching dynamic Copula model
TANG Tao, XIE Chi
(College of Business Management, Hunan University, Changsha 410082, China)
Ever since the foreign currency exchange rate system reform in 2005, the indeterminacy of RMB exchange rate and the foreign exchange risk have greatly increased. Hence, it is immediately imperative to strengthen foreign exchange risk management. Considering that hedge by using foreign currency futures contracts is an important means of managing the foreign exchange risk, we can develop a hedging model based on regime-switching dynamic Copula model to manage the foreign exchange risk. Firstly, we can describe the spot and futures marginal distributions of EUR, JPY, GBP, AUD and CAD by using GJR-t model. Secondly, we can introduce regime-switching dynamic Copula model to tell the dependence between the spots and futures of EUR, JPY, GBP, AUD and CAD. Finally, a comparative analysis is conducted between regime-switching dynamic Copula model and OLS, DCC GARCH, DCC Gaussian Copula model. The empirical results show that the regime switching dynamic Copula model is superior to other models in the effect of hedging, and that hedging can mitigate the foreign exchange risk effectively.
hedging; exchange rates risk; regime switching; dynamic Copula model
F832.5
A
1672-3104(2015)01−0104−07
[编辑: 苏慧]
2014−10−08;
2014−11−25
国家自然科学基金项目(71373072);国家自然科学基金项目(71340014);高等学校博士点专项科研基金项目(20130161110031)
唐韬(1983−),男,湖南永州人,湖南大学工商管理学院博士研究生,主要研究方向:企业风险管理;谢赤(1963−),男,湖南株洲人,博士,湖南大学工商管理学院教授,博士生导师,主要研究方向:金融工程与风险管理

