Two Types of Adaptive Generalized Synchronization of Chaotic Systems

LIU Jia（刘 佳），GUO Liuxiao（过榴晓），JIANG Zhengxian（江正仙）

School of Science，Jiangnan University，Wuxi 214122，China

Introduction

During the past decades，chaotic motion［1-3］has been extensively studied by researchers from distinct points of view.In 1995，Rulkov et al.［4］firstly described the generalized synchronization（GS）phenomenon and presented the idea of mutual false nearest neighbors to detect GS in experimental work.Compared with complete synchronization（CS），GS has much more complexity and mystery.In 1996，Abarbanel et al.［5］suggested the auxiliary system method and studied GS in driveresponse systems.The theory of auxiliary system method is given in Ref.［6］.So et al.［7］and Barreto et al.［8］showed that coupled systems which lacked intrinsic symmetries could exhibit synchronization sets with very complicated structures.Recently，Hramov et al.proposed a modified system approach to study the GS［9］.Based on this modified method，we have analyzed the mechanism of two types generalized synchronization of unidirectional coupled chaotic nonlinear systems［10］.

Recently，the design of synchronization in coupled chaotic systems is one of the main problems in the study of chaos synchronization.The difficulty in estimating a value of coupling coefficient for the coupled systems is avoided by using a kind of adaptive scheme，which is proposed by Huang et al.［11］In this paper，the schemes of adaptive GS and its mathematic mechanism will be presented.

The rest of the paper is organized as follows.In section 1，an adaptive scheme for GS is proposed.And the sufficient conditions for the existences of two types of the smooth and exponential attractive inertial manifolds of GS are theoretically given when the modified response system collapses to an asymptotically stable equilibrium and periodic orbit.In section 2，the two types of adaptive GS between Lorenz and RÄossler systems are presented to verify the theorems.Section 3concludes the paper.

1 Adaptive Scheme for GS of Chaotic Systems

In present paper，we consider a class of unidirectionally coupled chaotic systems（master-slave configurations）：

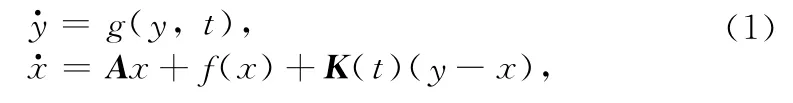
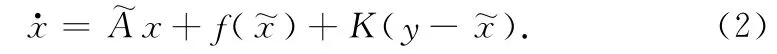
The adaptive coupling strength K（t）is designed as follows：

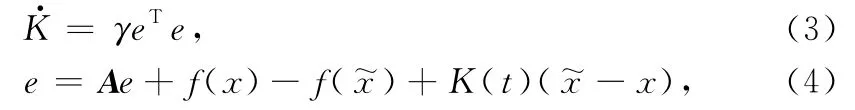
Generally，for the vector function f（x），the following assumptions are made.

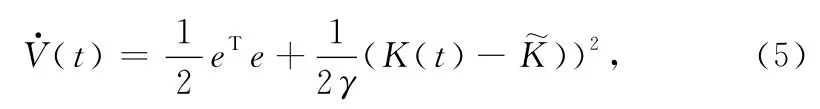
Corollary 1.

Theorem 1 If the function f（x）of dynamical system（1）satisfies Assumption 1，then the system（4）has an asymptotically stable equilibrium 0for any initial values under the adaptive control（3），and e →0，K（t）→K（∞）as t→∞.

Corollary 1 The maximum value of K（t）≥0is K（∞）and the minimum value is K（0）.

1.1 Adaptive equilibrium GS manifold

Theorem 1 gives the existence of GS manifold，but the smoothness and exponential attractive properties are not obtained.Hramov et al.［9］put forward a modified approach to study GS manifold.The dynamics of the response system may be considered as the non-autonomous dynamics of the modified system：

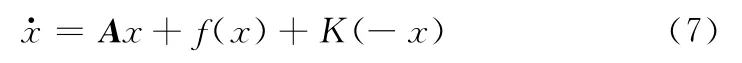
under the external force K（-x）.Subsequently，Yang et al.［3］numerically studied the roles played by drive and response systems on GS based on modified approach.Based on the modified approach，three types of GS are classified：equilibrium GS，periodic GS and C-GS，when the modified system has an asymptotically stable equilibrium，asymptotically stable limit cycles and chaotic attractors，respectively.The existence of first two types of smooth and exponential attractive adaptive GS manifolds will be proved.

Without loss of generality，suppose the modified system has the equilibrium point x0＝0（if x0≠0，we'll linearly transform Eq.（4）such that 0is its equilibrium point）.The system（4）can be rewritten as

where B＝A-K（∞）＋f′（0），F（x，t）＝f（x）-f′（0）x＋K（∞）x-K（t）x.

Obviously，all the eigenvalues of matrix Bhave the negative real part.Now the drive and response systems are denoted as

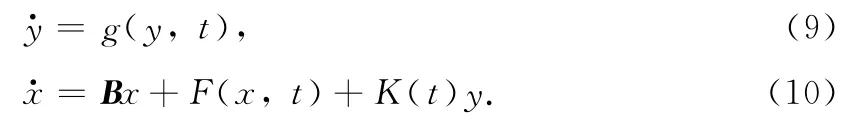
Theorem 2 In systems（6）and（7），all the eigenvalues of matrix Bhave the negative real parts，F：，and g：are sufficiently smooth function.Suppose the following conditions are satisfied：

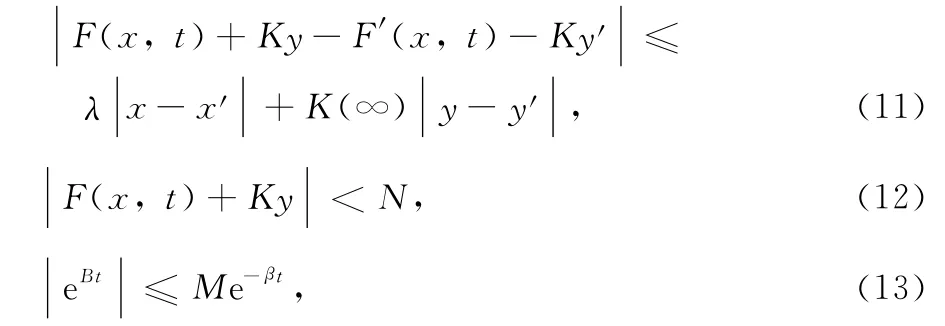
Proof Supposeσis the Lipschitz function，denoting that σ ∈FD，Δif and only if

holds for any y，y′.Defining the distanceσ（y）on the FD，Δit is easy to verify that FD，Δis a complete metric space.And if t ≤τ，y（τ）＝η ∈，there exists the solution y（t）＝y（t，τ，η）of Eq.（6）on（-∞，τ）.

where y（s）＝y（s，τ，η）.

We'll first prove the following result.The operator Gis compressive，which maps FD，Δon FD，Δ.In fact，

Supposeσandσ′are two maps satisfying system （11），η，η′∈，and let y（t）＝y（t，τ，η），y′（t）＝y（t，τ，when t ≤τ.We have

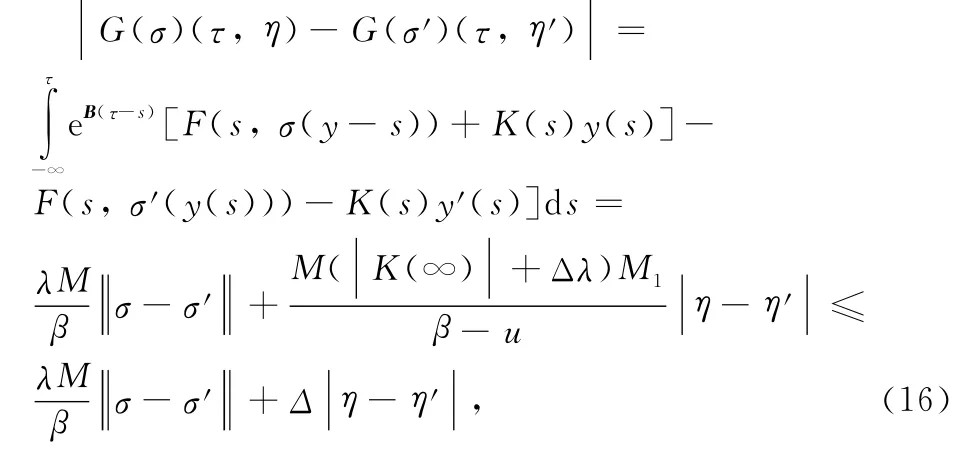
then the operator Gis Lipschitz compressive on FD，Δand has a fixed pointσ，i.e.，there exists a GS manifoldS ＝ ｛t，σ（y）， ｝y .The fixed point ■4 is also a Lipschitz function with respect to t.In fact，it is defined thatσhis satisfying system（11），and yh（t）is well posed solution of＝g（t＋h，σh（（t，y），y）），t＜τ，y（τ）＝η，

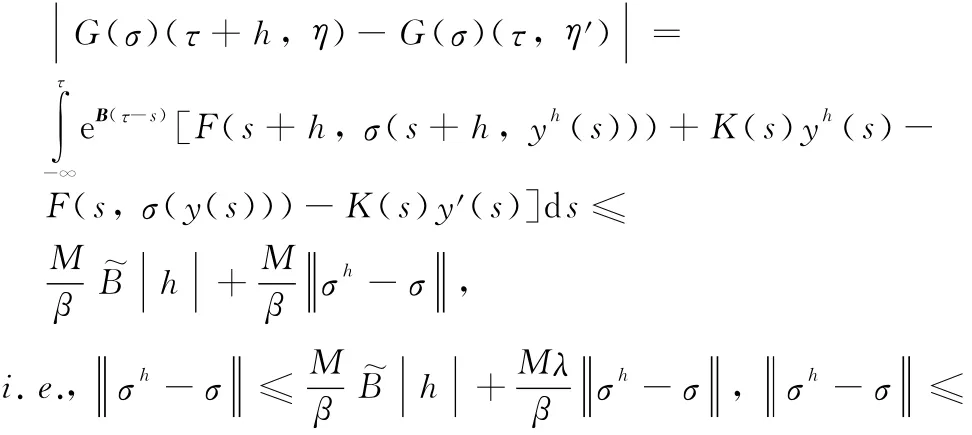
Theorem 3 The GS manifold is exponentially attractive under the conditions of Theorem 2，and satisfies x（t）-where x（t）and y（t）are the solutions of systems（5）and（6）.

当急性中毒患者经积极救治、病情稳定后，护士应做好患者的病情恢复管理工作，主要从康复锻炼、饮食指导方面入告知患者应摄入合理的饮食，保持营养的均衡丰富，有利于促进机体免疫功能的恢复；同时在病情恢复即开始进行康复锻炼，促进血液运行，有利于增强机体抵抗力，减少住院时间；出院时统一对患者进行健康宣教，告知其注意增强自我防护、自我保健意识等。

1.2 Adaptive periodic GS manifold

We consider that the modified system（7）has asymptotically stable periodic solution（t）＝（t＋T），where T ＞0.We will introduce two lemmas［12］to prove the existence of periodic GS manifold.

Lemma 1

is a linear periodic differential equation，where A（t）is a continuous function，A（t＋T）＝A（t），T ＞0.Then there exists a continuous function Z（t）with period T，and under w（t）＝Z（t）x，Eq.（14）can be transformed to

where Bis a constant matrix.

Lemma 2 Suppose the real parts of eigenvalues of matrix B in Eq.（15）areβ1，β2，…，βn，and the eigenvalues ofareα1（t），α2（t），…，αn（t）.Then there exists a unitary matrix S（t）＝（Si，j（t））such thatβi＝（t）dt，i＝1，2，…，n.Let e（t）＝x（t）-（t），and then

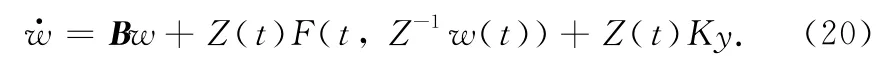
The corresponding GS manifold x（t）＝（t）＋σ（y（t））near（t）is transformed to e（t）＝Z-1（t）w（t）＝σ（t，y（t）），w（t）＝Z（t）σ（t，y（t））＝Σ（t，y（t））.

It is obvious that the existence of adaptive smooth equilibrium GS manifold in

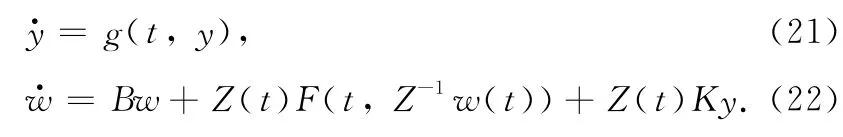
Similarly，we obtain Theorem 4.

Theorem 4 In systems（18）and（19），all the eigenvalues of matrix Bhave the negative real part，and F：and g：are sufficiently smooth functions.Suppose the following conditions are satisfied：

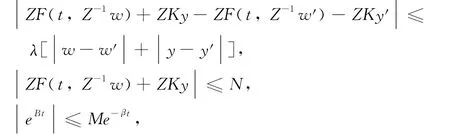
whereλ，M，M1，N，β，μ，D，andΔ are non-negative constants.Then there exists a smooth GS manifold，S ＝satisfy-

e.the second type of smooth GS manifold（periodic GS）x（t）＝（t）＋σ（t，y（t））＝（t）＋Z-1Σ（t，y（t））exists in systems（18）and（19）.

Theorem 5 The GS manifold is exponentially attractive under the conditions of Theorem 4，and satisfies

where x（t）and y（t）are the solutions of Eqs.（18）and（19）.

2 Numerical Examples

We take classical chaotic Lorenz system as the drive oscillator and take RÄossler system as the response system under adaptive coupling strength，which are described as：

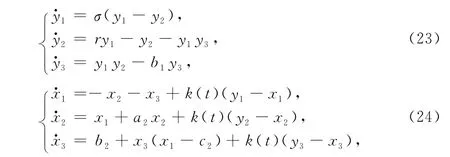
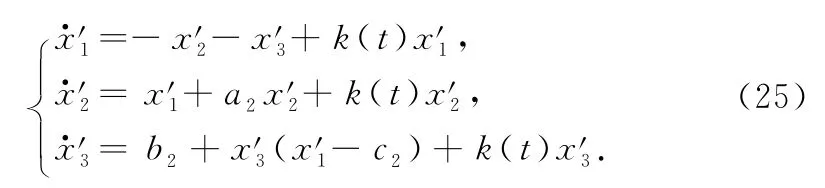
（The first kind of GS manifold）Choose the initial value（y1，y2，y3，x1，x2，x3，z1，z2，z3，k，x′1，x′2，x′3）（0）＝（1，2，3，4，5，6，2.1，3.1，4.1，1，2，3，1）.In this case，the system（22）collapses to an asymptotically stable equilibrium（-0.008 4，-0.009 8，0.018 2）.Let the parameter r＝0.2.The response system（24）and the auxiliary system （25）carry out CS，which is shown in the Fig.2.Based on the auxiliary system method，we have that the driving systems（23）and response system （24）realize GS（see Fig.3）.The adaptive coupling k（t）is shown as Fig.4.

Fig.1 Attractor of the drive Lorenz system

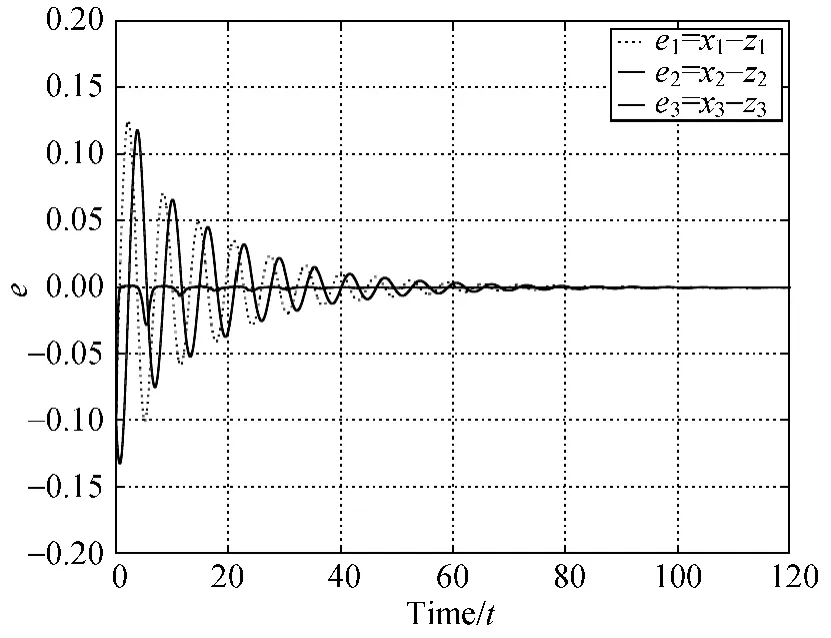
Fig.2 Graphical representation of errors between the response system （24）and auxiliary system（25）

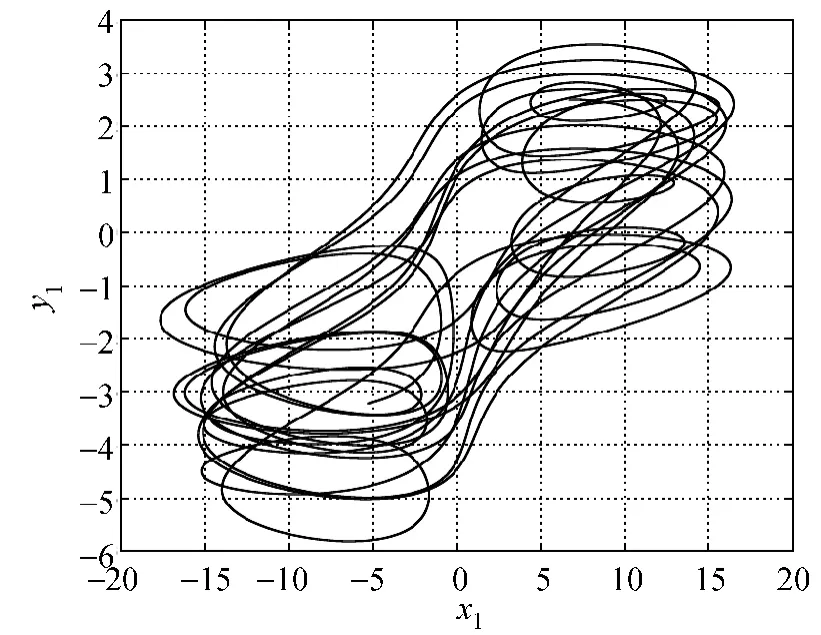
Fig.3 GS of a Raossler system （drive）and a Lorenz system （response）（Lorenz y1 vs RÄossler x1）

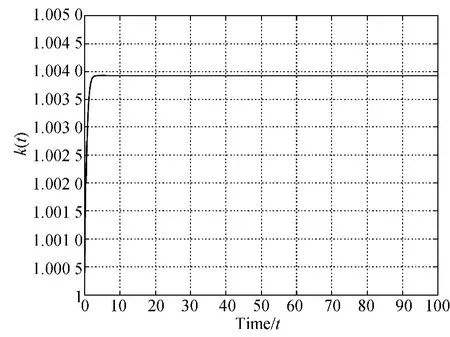
Fig.4 The adaptive update laws of k（t）when r ＝0.2

（The second kind of GS）In this case，the modified system （22）collapses to asymptotically stable periodic orbits（see Fig.5）.We choose the initial value and（y1，y2，y3，x1，x2，x3，z1，z2，z3，k，x′1，x′2，x′3）（0）＝（1，2，3，4，5，6，4.11，5.21，6.31，0.03，1，1，1）.The results are shown in Figs.6-7.From the above figures，we can see that the response and driving systems achieve two kinds of GS.

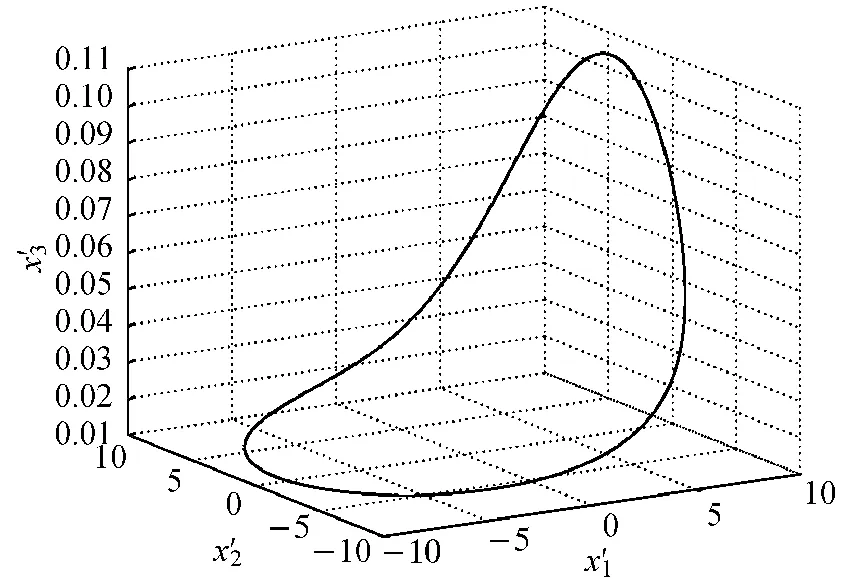
Fig.5 The modified system of Eq.（22）

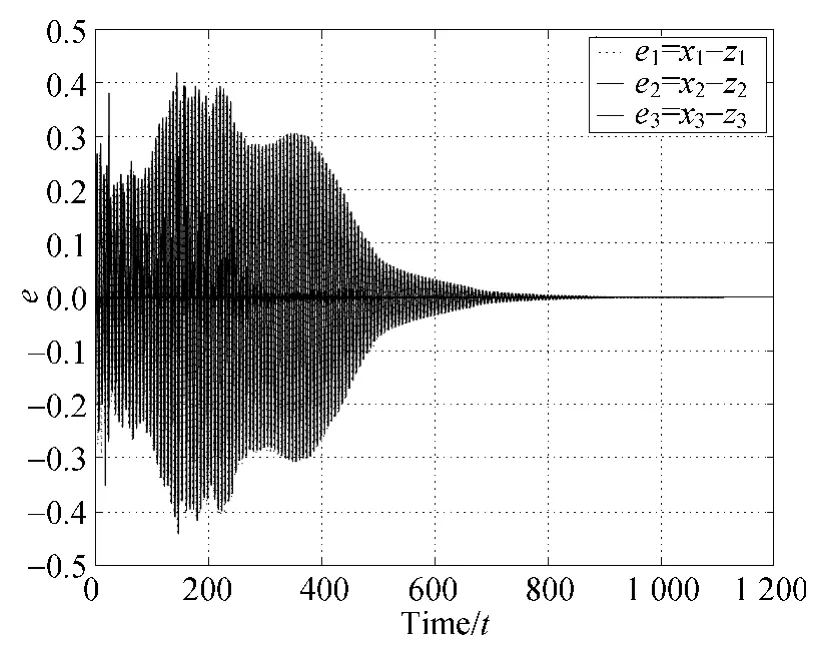
Fig.6 Graphical representation of errors between the response and auxiliary system

Fig.7 The adaptive update laws of k（t）when r ＝0.01

3 Conclusions

The schemes of adaptive generalized synchronization and its mathematic mechanism have been presented in this paper.The efficient conditions for the existences of the two types of smooth and exponential attractive inertial manifold of GS are theoretically given based on the modified system method.Future work will be the analysis of adaptive bi-coupled GS and so on.

［1］Pecora L M，Carroll T L.Synchronization in Chaotic Systems［J］.Physical Review Letters，1990，64（8）：821-824.

［2］Aziza H N.Chaos Synchronization of Lü Dynamical System［J］.Nonlinear Analysis，2004，58（1／2）：11-20.

［3］Yang J Z，Hu G.Three Types of Generalized Synchronization［J］.Physics Letters A，2007，361（4／5）：332-335.

［4］Rulkov N F，Sushchik M M，Tsimring L S.Generalized Synchronization of Chaos Indirectionally Coupled Choatic Systems［J］.Physical Review E，1995，51（2）：980-994.

［5］Abarbanel H D I，Rulkov N F，Sushchik M M.Generalized Synchronization of Chaos：the Auxiliary System Approach［J］.Physical Review E，1996，53（5）：4528-4535.

［6］Kocarev L，Parlitz U.Generalized Synchronization，Predictability，and Equivalence of Unidirectionally Coupled Dynamical Systems［J］.Physical Review Letters，1996，76（11）：1816-1819.

［7］Ott E，So P，Barreto E，et al.The Onset of Synchronization in Systems of Globally Coupled Chaotic and Periodic Oscillators［J］.Physica D：Nonlinear Phenomena，2002，173（1／2）：29-51.

［8］Barreto E，Josic K，Morales C J，et al.The Geometry of Chaos Synchronization［J］.Chaos，2003，13（1）：151-164.

［9］Hramov A E，Koronovskii A A.Generalized Synchronization：a Modified System Approach［J］.Physical Review E，2005，71：067201.

［10］Guo L X，Xu Z Y.HÄolder Continuty of Two Types of Generalized Synchronization Manifold［J］.Chaos，2008，18（3）：033134.

［11］Huang D.Adaptive-Feedback Control Algorithm ［J］.Physical Review E，2006，73：066204.