金属管材拉伸强度测试的不确定度评定

许志敏

（湄洲湾职业技术学院，福建莆田351254）

金属管材拉伸强度测试的不确定度评定

许志敏

（湄洲湾职业技术学院，福建莆田351254）

文章从金属管材试样拉伸强度的试验方法入手，对其拉伸强度测试结果不确定度的产生因素进行了分析。同时，文章还在分析的基础上建立了相应的数学模型，对管材拉伸强度测试的不确定度进行评价。

金属管材;拉伸强度;不确定度;数学模型

作为材料验收及工艺设计的关键参数之一，拉伸强度测量结果的准确度直接影响到金属管材的评价。不确定度作为试验结果可信赖程度的表征方式，一方面为了方便使用它的人员评估其可信度，另一方面也提高了测量结果之间的可比性。由此，不确定度成了评价金属管材测量结果的重要指标之一。

文章从金属管材拉伸强度的测试方法及相应测试设备入手，对测试过程中的影响因素分析确认、构建数据模型，对合成标准不确定度进评价。

1.不确定度来源分析

按照《金属材料拉伸试验第一部分:室温试验方法》（GB/T 228.1-2010），拉伸强度测试系在规定的试验环境下用拉力拉伸试样，直至断裂，按标准定义对数据进行测定[1]。通过对试验方法进行分析，拉伸强度的不确定度主要来源于测量设备、取样及样品加工等。

目前不确定度的评定方法主要有A类与B类两种，A类不确定度评定方法采用实验标准偏差来表征，需要在试验结束后方能得出；B类不确定度评定则是从试验方法及试验设备等参数建立数据模型进行估计。文章主要是根据抗拉强度的测量及计算方法对其测量的不确定度进行评定，即文章采用了B类的评定方法。取样及样品加工主要涉及到批量测量时数据的稳定性，主要影响到A类测量不确定度的评定，与B类测量不确定不存在直接关系。文章确定测量设备为金属管材拉伸强度测量不确定度的来源，具体影响因素主要包括尺寸测量与力值测量。

2.测量数学模型

在拉伸试验中，管材的抗拉强度主要通过拉伸力值与试样原始横截面积按式（1）计算。

式中：

Rm为抗拉强度，单位为MPa；

Fm为最大力,单位为N；

S0为原始横截面积，单位为mm2。

管材试样原始横截面积按式（2）计算。

式中：

S0为原始横截面积，单位为mm2；

a0为原始管壁厚，单位为mm；

D0为原始管外直径，单位为mm。

v综合式（1）与式（2），管材抗拉强度的合成计算公式如式（3）。

式中：

Rm为抗拉强度，单位为MPa；

Fm为最大力,单位为N；

S0为原始横截面积，单位为mm2；

a0为原始管壁厚，单位为mm；

D0为原始管外直径，单位为mm。

3.测量不确定度评价

由式（3）分析可知，金属管材抗拉强度的不确定度主要由最大力、原始管外直径及原始管壁厚因素决定。由此，文章从以上三个因素出发按B类评定方法对金属管材抗拉强度的不确定度进行分析。

3.1 最大力不确定度的B类评定

3.2 原始管外直径的B类评定

3.3 原始管壁厚的B类评定

3.4 合成标准不确定度

按GB/T 228标准，最大力、原始管外直径及原始管壁厚因素均为独立测量的数据量，所以，上述三项标准不确定度分量之间不相关。由此，金属管材的合成标准不确定度可表示为：

3.5 扩展不确定度

取置信概率p=95%，按照JJF1059-2012《测量不确定度评定与表示》确定包含因子k=2.0[2]，相对扩展不确定可表示为：

4.不确定度分析在测量中的应用

假定材料试验机的求值误差为0.01%，千分尺示值误差为0.006%。则基于B类评定的管材抗拉强度扩展不确定度为0.015%。

同时，使用该组测量设备进行测量时，在置信概率为95%的情况下，其测量值Rm′与真实值Rm之间的关系为：

5.结论

抗拉强度虽是金属管材的固有属性之一，但是在实际测量中由于受到测量设备、环境、取样方式、加载方式等各种外来因素的影响，其试验结果存在着一定的不确定性。文章从测试设备角度出发以不确定度分析的方式对该因素可能产生的不确定性进行了分析，建立出相应的测量数学模型，并在该基础上得出扩展不确定度的评价方式。

[1]国家标准化技术委员会.GB/T 228.1-2010，金属材料拉伸试验第一部分:室温试验方法[S].北京：中国标准出版社，2010.

[2]国家标准化技术委员会.JJF1059.12012，测量不确定度评定与表示[S].北京:中国计量出版社,2012.

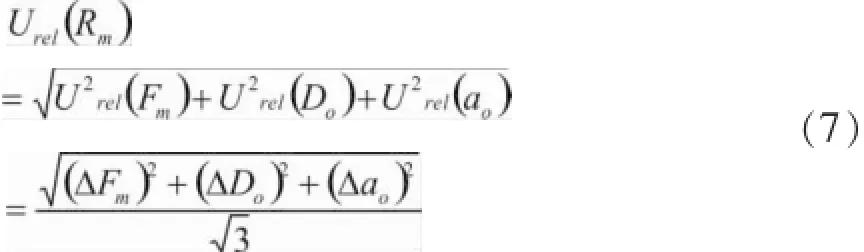
（责任编辑：仇富强）

TH87

A

1671-752X（2015）04-0041-02

2015-08-21

许志敏（1979-），男，福建莆田人，湄洲湾职业技术学院机械工程系讲师，技师，研究方向：机械设计、结构分析与测试技术。