随机需求和生产成本同时扰动时供应链的协调应对

徐 红 （盐城工学院 管理学院，江苏 盐城224001）

XU Hong (School of Management, Yancheng Institute of Technology, Yancheng 224001, China)

0 引 言

供应链是一个系统，需要供应链中各节点企业互相协调和合作，才能减少各成员之间的冲突，减少双重边际效应的影响，供应链的整体绩效才能得到更好的提升和优化。然而，近年来突发事件发生的频率不断增加，往往对企业在处理突发事件时的应对能力带来了严峻的考验。它不仅会造成市场需求的激烈变化、原材料供应的延迟、生产成本的急剧上升以及工人罢工等问题, 而且供应链系统原来的协调会被打破，供应链上各节点成员的生存与发展都将产生致命的打击。如“512”汶川地震期间，由于基础设施的严重受损，电力供应无法保证，四川什邡的10 万吨锌冶炼产能受到严重影响，四川省内多数锌矿和铅矿被迫关闭，造成部分锌冶炼厂停产，锌供应链中断。这表明供应链外部环境处在不断的变化之中；突发事件对供应链造成影响的广度和深度都有所加剧，供应链在应对突发事件时变得更加脆弱。

因此，风险管理及供应链突发事件管理日趋重要，特别是对相关突发事件的管理研究已成为供应链管理环境中新的发展趋势，具有重要的理论和实践价值。Causen 等人[1]于2001 年首先提出突发事件应急管理这个概念，其思想在航空公司的应急领域中得到很好的应用[2-3]，随后在物流配送、供应链管理、项目管理等领域有了较为广泛的应用[4-6]。对于如何运用契约机制协调应对供应链突发事件的研究目前还处于起步阶段，在研究的广度和深度上均需要不断地拓展。Qi[4]等人基于一个二级的供应链，研究了线性需求函数下，运用数量折扣契约来协调供应链的突发事件，并使供应链期望利润实现最大化；于辉[6-7]等人分别在确定性需求和随机需求条件下，提出了利用改进的数量折扣契约和回购契约建立应对突变风险的协调机制；Xiao[5]等分别研究了两个零售商竞争时以及生产成本和需求同时变化时，通过批发价加补贴率合同来实现供应链的协调；马成，周永务[7]等人将期权契约引入两阶段的供应链中，研究突发事件导致制造商生产成本、零售价格同时变化时供应链的协调应对。胡劲松[8]等人将二级供应链扩展为三级供应链，在考虑随机需求条件下，探讨突发事件对其的影响，通过将价格折扣契约中的参数重新设计来协调供应链。雷东[9]等假定线性需求函数时，即突发事件导致市场需求的规模和生产成本同时发生变化时供应链的协调应对。王玉燕[11-12]等人针对突发事件下闭环供应链的协调进行了研究，提出可以调整原来的收益共享契约及回购契约协调应对突发事件。覃艳华[13]等人研究了随机性需求下，如何调整回馈与惩罚契约来协调闭环供应链的突发事件。从上述文献中可以看出，国内外学者对突发事件供应链的协调进行了多方面的研究，但是对突发事件造成的随机需求和生产成本同时扰动时供应链的协调问题研究得比较少。关于回馈与惩罚契约如何应对突发事件导致的多行为因素的研究更是比较少见。回馈与惩罚契约机制由于能够更好地刺激销售商增加订购量、降低监督成本，目前在软件、汽车等行业得到了广泛的应用，越来越受到人们的重视。本文在上述文献研究的基础上，拟探讨随机市场需求下，突发事件导致市场需求和制造商的生产成本同时发生变化时对供应链的影响，并运用改进的回馈与惩罚契约协调突发事件下供应链的应对。

1 稳定环境下供应链的回馈与惩罚契约模型

考虑由单个制造商和单个零售商组成的短生命周期商品的供应链，在这个系统中，制造商利用原材料生产产品，零售商将产品销售给客户。在产品的生产和销售中，假设所有的信息是对称的，制造商和零售商彼此都知道对方的需求、成本结构等信息，双方都以利润最大化作为自己的决策目标。根据上述说明，给出各相关参数定义如下：

制造商单位产品的生产成本为c；给予零售商单位产品的批发价是w；零售商的零售价格为p，它是固定的，由市场竞争形成；零售商因为产品销售出现短缺时而导致的单位产品的惩罚为br；期末库存时单位产品的残值为h；Q为零售商根据市场需求预测确定其产品订货量；假设市场需求x是一个连续的随机变量，其均值为φ；密度函数和累计分布函数分别为f（x） 、F

假设S（Q）为零售商的期望销售量，则为销售季末的期望剩余产量，则为销售季末没有满足的期望需求量，则根据一般的常识有

在供应链中，制造商是领导者，他首先给零售商设定某一销售目标为T，当最终的销售量达到（1+ψ）T时，制造商根据增量给予零售商单位回馈为θ，而当最终的销售量没有达到规定销售目标时，仅为时，制造商根据不足部分对零售商的单位惩罚也为θ，这里ψ≥0, 1≥ξ≥0。供应链成员的决策顺序为：在销售季节开始前，制造商首先对零售商的市场需求进行调研和分析，然后提供相应的契约（w,T,）θ ；零售商对市场需求进行研判后可以选择接受或拒绝，若接受该契约，就要确定自己的最优订货量；制造商根据零售商的订单安排生产计划，零售商销售产品以满足消费者的需求。设制造商、零售商和供应链的期望利润分别为πm,πr,πs，则根据前面的假设得到：

因为πr是关于Q的凹函数，所以对式（2） 求对Q的导数，得：

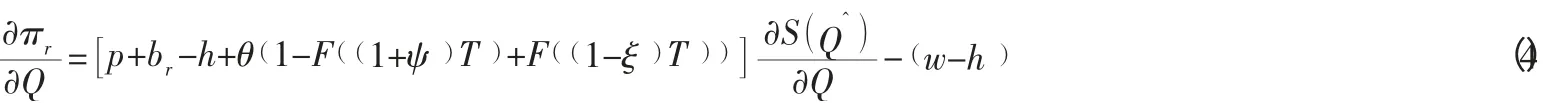
对式（3） 求Q的导数，得到供应链的最优生产量是：

比较式（4） 和式（5） 可以发现，若要使供应链达到协调，即零售商的订货量为供应链系统的最优生产量，当θ时，零售商的最优产品订购量与供应链的最佳生产量一致，回馈与惩罚契约能够实现供应链的协调。

2 突发事件对供应链的影响

在稳定的环境下，制造商的生产计划是以零售商最优的订购量为基础的，确定好生产计划后，在销售季节来临前，突发事件发生了，外部环境的变化导致零售商所面临的市场需求出现相应的变化，市场需求分布函数由F变为G，供应商的生产成本从c变为c+Δc。设新的市场需求的密度函数和累计分布函数分别变为其均值变为φG，则此时

突发事件发生后，如果原计划的Q^不再是新供应链的最佳生产量（也是零售商的最优订购量） 时，就会出现缺货成本等。当新的产品订货量Q＞Q^时，必须增加机器设备、原材料、人力等以扩大生产来满足市场增加的需求，设增加的产品需要增加单位生产成本为λ1；当新的产品订货量时，多余的产品要储存或降价打折等，设新的单位处理费用为λ2。此时零售商的期望利润制造商的期望利润和供应链的期望利润分别为：

证明：首先证明对于任意的Q≥0，如果采用反证法，假设突发事件致市场规模增加时，有Q*≤Q^。此时，供应链的期望收益为：

下面我们讨论市场需求和制造商的生产成本同时发生扰动时，供应链的最优决策及协调策略。

定理1 突发事件引起零售商面临的市场需求和制造商的生产成本同时变化时，供应链的最优订货量为：

其中：Q'是方程的解，Q''是方程的解。

证明：当市场需求的规模因突发事件的发生增加时，由引理可知Q*＞Q^，此时供应链的期望收益函数为：

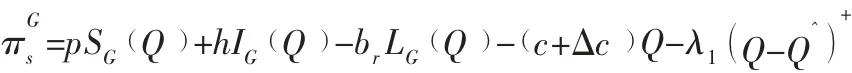
当市场需求的规模因突发事件的发生而减少时，由引理可知Q*≤Q^，此时供应链的期望收益函数为：

当突发事件造成市场规模增加较少时，它使得Q''≥Q^。因为是严格凹的，所以它在[0,Q'') 是增函数，同时由于约束条件Q≤Q^，所以Q*=Q^为供应链的最优订货量。

定理2 突发事件造成市场需求和制造商的生产成本同时发生变化时，如果原来的回馈与惩罚契约不变化，供应链将不再协调。

证明：当突发事件发生后，如果原来的回馈与惩罚契约不变，则此时零售商的期望收益为：

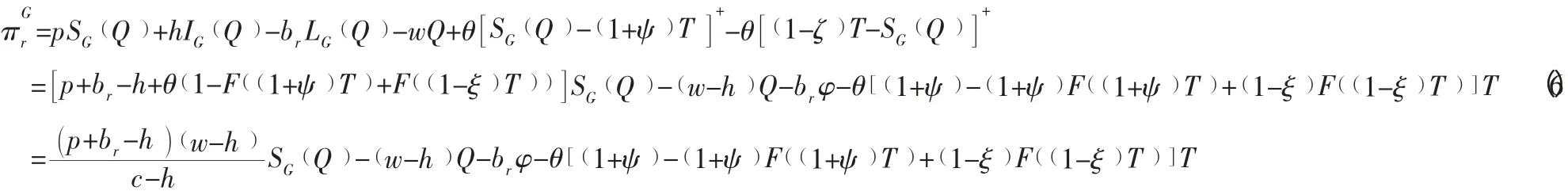
对式（6） 求关于Q的二阶导数，可知因此可得零售商的最优订购量

当市场需求因突发事件的发生而增加时，供应链的期望收益为：

同理可以发现当市场需求的规模因突发事件的发生而减少时，原有的契约不能再发挥协调作用。

3 协调应对突发事件

由定理2 可知，当突发事件引起零售商面临的市场需求和制造商的生产成本同时变化时，原来的回馈与惩罚契约不能再发挥协调作用。因此，要使供应链能够协调，原来的契约必须进行相应的改变。

当突发事件引起市场需求增加的规模比较大时，由定理1 可知要实现供应链的协调，则一定要成立。从中可以得到：

同理可得，当突发事件引起市场需求减少的规模比较大时，要实现供应链的协调，则必须成立。从中可以得到

由此可得：当突发事件导致零售商面临的市场需求和制造商的生产成本同时扰动时，变化后的回馈与惩罚契约能够实现供应链的协调，这时：

4 结束语

本文考虑随机性市场需求时，如何利用回馈与惩罚契约来协调应对突发事件。研究结果表明：当突发事件造成零售商面临的市场需求和制造商生产成本的变化满足一定的条件时，原有的回馈与惩罚契约仍能实现供应链的协调。而当零售商面临的市场需求和制造商的生产成本变化超过一定阀值时，原有的回馈与惩罚契约不再具有协调作用，但通过对原来的回馈与惩罚契约中的参数进行重新设计，供应链依然能够实现协调。当然，本文只考虑了单一制造商和零售商构成的供应链，但在实践中，供应链是一个复杂的动态系统，如多制造商或零售商、多阶段的供应链等也是比较普遍的；突发事件的发生可能会导致供应链系统中的多个因素如制造商生产成本、零售商购买成本、市场需求等同时变化，也可能会使各因素同时扰动且变化后的因素为不对称信息，考虑供应链成员的风险偏好等。因此，如何利用回馈与惩罚契约来协调复杂情况下供应链应对突发事件将是下一步研究的方向。

[1] Causen J, Hansen J, Larsen J. Disruption management: Operations Research between planning and execution[J]. OR/MS Today, 2001,28(5):40-43.

[2] Thengvall B, Bard J F, Yu G. Balancing user preferences for aircraft recovery during airline irregular operations[J]. IIE Transactions on Operations Engineering, 2000,32(3):181-193.

[3] Yu G, Arguello M, Song M, et al. A new Era for crew recovery at continental airline[J]. Interfaces, 2003,33(1):5-22.

[4] Qi X T, Bard J, Yu G. Supply chain coordination with demand disruptions[J]. Omega, 2004,32(4):301-312.

[5] Xiao T J, Yu G, Sheng Z H, et al. Coordination of a supply chain with one-manufacturer and two-reailers under demand promotion and disruption management decisions[J]. Annals of Operations Research, 2005,135(1):87-109.

[6] 于辉，陈剑，于刚. 协调供应链如何应对突发事件[J]. 系统工程理论与实践，2005,25(7):9-16.

[7] 马成，周永务. 期权契约下应对突发事件的供应链协调[J]. 合肥工业大学学报，2009,32(3):430-434.

[8] 胡劲松，王虹. 三级供应链应对突发事件的价格折扣契约研究[J]. 中国管理科学，2007,15(3):103-107.

[9] 雷东，高修成，李建斌. 需求和生产成本同时扰动时的供应链协调[J]. 系统工程理论与实践，2006,26(9):51-59.

[10] 杨智辉，陈宏,等. 随机需求和生产成本同时扰动下的供应链波及效应[J]. 管理学报，2010,7(5):728-732.

[11] 王玉燕. 收益共享契约下闭环供应链应对突发事件的协调分析[J]. 中国管理科学，2009,17(6):78-83.

[12] 王玉燕. 回购契约下闭环供应链对突发事件的协调应对[J]. 运筹与管理，2009,18(6):46-52.

[13] 覃艳华,等. 回馈与惩罚契约下闭环供应链应对突发事件的协调性研究[J]. 管理工程学报，2012,26(3):96-100.

[14] 吴忠和,等. 需求和生产成本同时扰动下供应链期权契约应对突发事件[J]. 中国管理科学，2013,21(4):98-103.