闭环供应链系统环境——经济双向控制模型体系

郑 飞 （佛山广播电视大学，广东 佛山528000）

ZHENG Fei (Foshan Radio & Television University, Foshan 528000, China)

0 引 言

20 世纪80 年代末期，我国环保专家针对日益出现的严重环保问题，提出了环境——经济系统双向控制的基本思想，以经济状况的调查和评价为基础，通过经济发展预测，从而实现经济发展的环境保护战略，对环境——经济系统实现正向控制；与此同时，以环境质量监测与评价为基础，通过环境发展预测，从而对经济发展进行控制与约束，对环境——经济系统实现反向控制；而且以正向控制为主，反向控制为辅。

20 世纪90 年代以来，随着传统经济模式向循环经济模式、低碳经济模式的转变，世界各国环保意思不断增强。与此同时，在互联网时代，产品个性化、更新换代不断加快等特点，使得各企业各自为政已经很难面对这种挑战，供应商、制造商、经销商以及回收商、再处理商必须通力合作与协调，实现经济与环境的协调发展。2003 年，Daniel 等提出了闭环供应链的思想，认为闭环供应链是企业从采购到最终消费的完整供应链循环，将正向供应链和逆向供应链紧密结合起来，不仅考虑传统正向供应链，而且考虑产品回收、再利用以及回收产品的分销处理。因此，闭环供应链的目标除了追求经济效益，实现企业经营的经济目标之外，还包括企业的可持续发展目标。

为了促进可持续发展战略的实现，本文结合闭环供应链的特点与目标，探讨闭环供应链系统经济发展与所处环境的双向控制问题，重点讨论相关的数学模型。

1 闭环供应链系统多级双向控制模型体系结构

由于闭环供应链系统，既兼顾正向供应链，取得经济效益，又兼顾逆向供应链，保护环境，实现低碳生产与生活，同时由于闭环供应链系统涉及到供应商、制造商、分销商、零售商、消费者和回收商等众多商业实体，闭环供应链系统是一个典型的大规模系统。因此我们从大系统控制的角度，来考虑闭环供应链系统的控制问题。根据大系统控制思想，可设计闭环供应链系统的多级环境——经济双向控制模型体系，如图1 所示。

在图1 中，最低级（第一级） 是闭环供应链系统环境——经济基本模拟与局部控制模型，它向上一级（第二级） 传递基础信息，通过大量基础数据的收集与分析，模拟闭环供应链系统经济发展与环境污染的状况，进行环境——经济系统的评价，并为第二级提供基本目标、约束条件及相关数据资料等，在这一级的经济模型中，我们选取闭环供应链系统经济发展协调预测模型和投入产出模型来进行经济分析，使用大气分散分析模型和水质分析模型进行环境分析。当它接受中间级要求，向下（实际被控对象） 执行具体控制时，则通过对供应商、制造商、经销商的相关活动如技术改造、原材料成份变化、替代品的开发、新产品开发、废弃物回收与利用、营销等手段来实现。

中间级（第二级） 为闭环供应链系统环境——经济协调双向最优控制模型。通过分析满足闭环供应链系统环境——经济多个目标的各种约束条件，通过最优化手段，既对环境——经济系统进行双向协调控制，又为第三级模型提出一系列环境——经济综合指标和可供决策的待选方案。

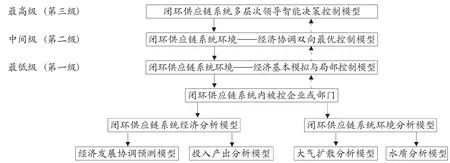
图1 闭环供应链系统环境——经济双向控制模型体系结构

第三级（最高级） 为多层次领导智能决策控制模型。该模型供领导层决策时依据客观条件的变化和实际可能，按智能推理方法，得出最佳的决策方案。

这三级模型融为一体，将定量分析与定性分析相结合，具有一定的实用价值。其中第二级模型是核心部分，起到承上启下的作用。

以下将主要讨论闭环供应链系统经济分析与环境分析模型的结构与应用方法。

2 闭环供应链系统经济发展协调预测模型

闭环供应链系统涉及到供应商、制造商、经销商、批发商、零售商、消费者及回收商等多个节点，各节点间相互影响、相互制约，因此对闭环供应链系统中各节点的产品或服务进行预测时，要充分注意其他经济条件及相关因素的协调关系，既应考虑单个节点企业的财务指标采用某种方法进行预测，又要从整个闭环供应链的角度进行供应商、制造商、销售商、回收商等节点的服务水平、产品品质、运营能力、信息机制、学习与创新能力等相关经济指标进行预测。尽管对闭环供应链系统经济发展的预测方法很多，但考虑到闭环供应链系统的复杂性，我们采用一种智能预测模型——模糊协调预测模型进行预测。

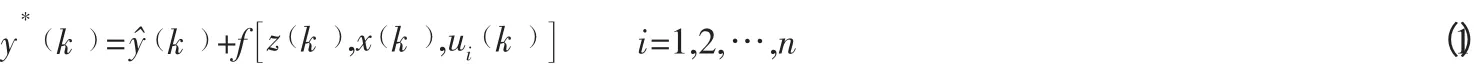
其中，k表示离散时间变量；y（k）表示k时刻闭环供应链整体财务指标值；f（.,., .）为协调校正系数；z（k）表示k时刻区域经济形势预测值；x（k）表示k时刻闭环供应链行业财务指标预测值；ui（k）表示k时刻其他相关经济指标预测值，i=1,2,…,n。

在模型（1） 中，f（.,., .）是模型的重要组成部分，其作用是在闭环供应链整体财务指标预测的基础上，通过适当的形式进行校正或补偿，反映各因素之间的协调关系。如令：

其中，α（k）为校正系数；G（k）为协调引导变量，它综合考虑了z（k）、x（k）、ui（k），从而一定程度上反映其协调关系。G（k）的表达式可有各种形式，如假设z（k）、x（k）、ui（k）与y（k）的协调关系分别记为y1（k）、y2（k）、y3（k），且：

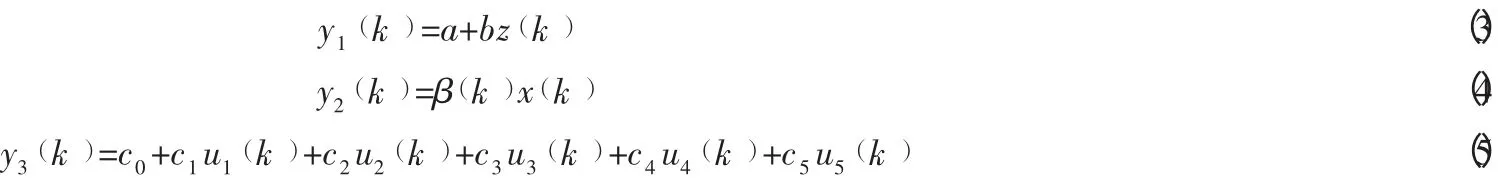
再令：

其中，z（k）表示闭环供应链所处地区的国内生产总值；β（k）为闭环供应链节点企业的产品市场占有率（若预测，可用预估值）；u1（k）表示闭环供应链节点企业的服务水平；u2（k）表示闭环供应链节点企业的产品品质；u3（k）表示闭环供应链节点企业的运营能力；u4（k）表示闭环供应链节点企业的信息机制；u5（k）表示闭环供应链节点企业的学习与创新能力；a,b,ci（i=0,1,2,3,4,5）为相应的回归系数。

因此，在闭环供应链节点企业的产品市场占有率确定的情况下，通过回归分析，按照（1） ～（6） 式，即可以进行闭环供应链的协调预测。

3 闭环供应链系统投入产出分析模型

投入产出分析是研究经济系统各个部分间数量关系以及再生产的综合比例关系的一种工具，用来综合考察经济系统各部分表现为投入与产出的相互依存关系。其主要内容是编制投入产出表，并建立相应的投入产出模型，进而进行经济分析。

为了达到环境——资源——经济协调，我们在建立闭环供应链系统环境——经济投入产出分析模型时，在此根据具体对象和任务，以经济分析为主，同时考虑资源回收、流失及环境污染治理问题，因而将资源流失量、环保投资及相关指数等引入到经典的投入产出模型结构中。

在制定闭环供应链系统环境——经济投入产出表（为了节省篇幅，此处略去） 时，很容易得到投入产出的平衡方程组：

投入产出行模型为：

投入产出列模型为：

其中，xij表示闭环供应链中某节点企业内部第i个部门（如：服装企业中的织布车间） 在一个生产周期（如：年、季、月）内对第j个部门的物料投入，这里不仅包括生产过程中的投入，也包括环境治理过程中的投入，同时还有自然的环境流失量等；Tpj表示闭环供应链中该节点企业上游第p个供应商在该生产周期内对其第j个部门产品的物料投入；yi表示节点企业内部第i个部门在该生产周期内最终产品数量；xi表示节点企业内部第i个部门在该生产周期内产品的总产量和总产值；表示节点企业内部第i个部门的产品在该生产周期内用于生产性消耗的数量；表示节点企业内部第j个部门在该生产周期内的产品中生产资料转移价值（包括节点企业直接上下游节点企业的所有物料投入）；Zj表示节点企业第j个部门在该生产周期内新创造的价值；Wj表示节点企业第j个部门产品在该生产周期内能源消耗、环保投资和固定资产折旧。

要达到投入产出平衡，必须满足：

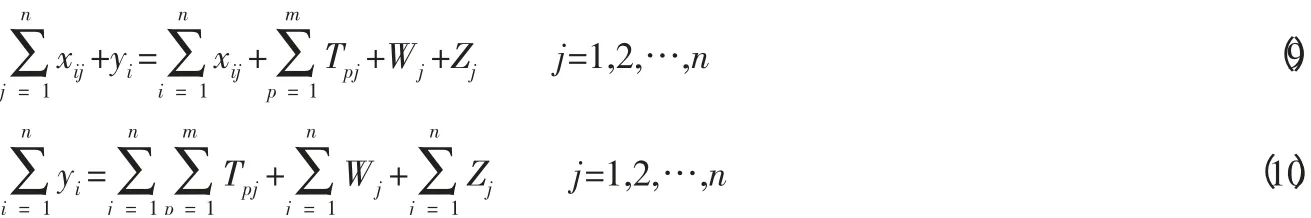
令节点企业内部第j个部门产品对第i个部门产品的直接消耗系数为aij，它表示j部门单位产品所消耗的i部门产品的数量，即：

则直接消耗系数矩阵为：

又令节点企业内部第j个部门对第i个部门的完全消耗系数为cij，它表示生产周期内节点企业内部j部门的单位产出直接和间接消耗的i部门产品的总量，即：

则完全消耗系数矩阵为：

4 闭环供应链系统环境分析模型

4.1 大气扩散分析模型。闭环供应链系统的逆向供应链子系统通过回收废弃物来减少资源的浪费，保护环境。我们选用常见的高价连续点源的地面浓度模型——正态烟云高斯模型进行大气扩散分析。即：

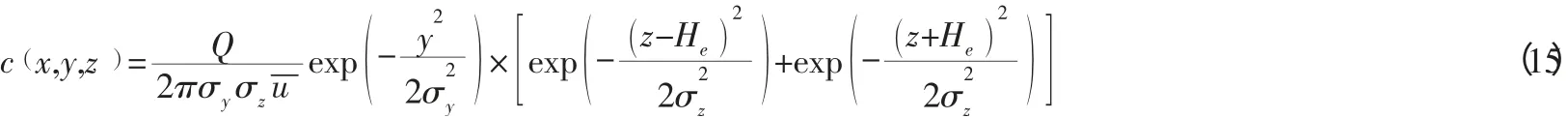
将大气稳定程度分为极不稳定、不稳定、中性和稳定4 个水平，并分别用符号S1、S2、S3和S4表示（这里当第i种稳定时，Si=1，其余为0），则大气污染浓度在不同时间条件下的短期预报模型为：

其中，v为风速；表示风向水平，F1为东风，F2为东南风，F3为南风，F4为东北风，F5为北风，F6为西北风，F7为西风，当出现第j种风向时，Fj=1，其余为0；使用加权最小二乘法估计得到参数a0,a1,a21,…,a24,a31,…,a37的值。例如某色织布厂在非采暖期的预报模型为：

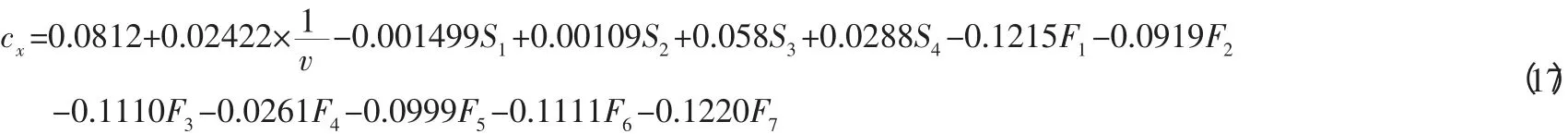
通过式（17） 即可以在相关气象预报的基础上，预报出SO2的污染浓度，并采取相应的预防与治理措施。

4.2 水质分析模型。对于河流水质模型，本文选用斯特利斯—菲尔普斯（S-P 方程） 的Thomas 改进型，即所谓的托马斯BOD-DO 模型，其基本方程为：

解得：

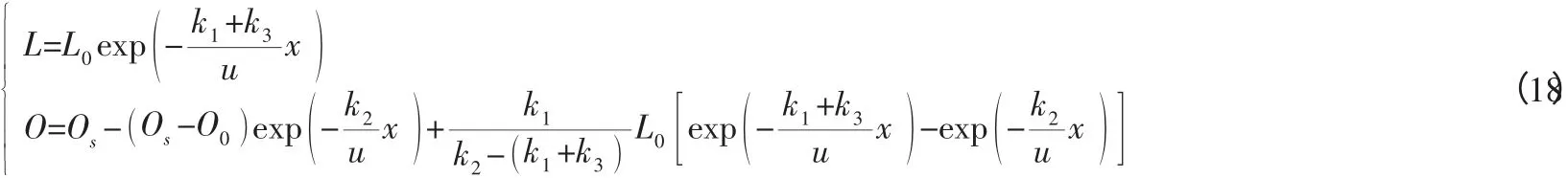
式中：L——距初始断面x处的BOD 浓度；L0——初始断面BOD 浓度；O——与初始断面距离x处的溶解氧浓度；u——断面平均流速；Os——水中饱和溶解氧浓度；O0——初始断面溶解氧浓度；x——河流沿程距离；k1——耗氧系数；k2——复氧系数；k3——沉浮系数。

根据模型（18），同时考虑排污口污染物浓度和排放量，并设河流按顺流方向排序，闭环供应链节点企业所处河流第i个断面水中某污染物的浓度ci，水流量为qi，则在污染状态相对稳定的情况下，下一断面i+1 处的浓度ci+1与ci间的关系满足：

其中：

这里，ci为断面的污染状态变量，ui为系统的控制变量。而Δqi表示断面处排污口污水排放流量；表示断面i到断面i+1之间河水的平均流速；Si+1,i表示断面i到断面i+1 之间的沿河距离；α 为自净系数；为稀释系数，表示在断面i处，ci浓度的河水与ui浓度的污水混和时的加权系数；表示污水从断面i流到断面i+1 在河水中停留的时间。例如某牛仔布厂利用该模型对某一水期河水的平均污染水平沿河流向的分布情况进行系统监测与研究，据此对上游各断面处污染物的浓度进行评估、预测，提出相应的治理方案。

5 结 论

本文研究了闭环供应链系统环境——经济双向控制的数学模型，重点研究了闭环供应链系统中节点企业的经济分析模型和环境分析模型。由于闭环供应链中各节点企业既相互独立又相互依存，因此在研究闭环供应链系统环境——经济双向控制的底层模型时，必须在大量数据资料的基础上，分别模拟节点企业的环境、经济现状，同时在进行经济协调预测时也要重视环境因素的影响；为了利用模型进行大气或环境的控制，有必要对产品的产量进行限制；为了达到环境——资源——经济协调发展，使用投入产出分析法进行综合评价。这些模型，可以应用于闭环供应链系统节点企业中，从而推动闭环供应链系统的不断完善与发展。对于闭环供应链系统环境——经济双向控制模型的第二级——闭环供应链系统环境——经济协调双向最优控制模型和第三级——闭环供应链系统多层次领导智能决策控制模型，限于篇幅，将在另文讨论。

[1] 汤兵勇. 市场经济控制论[M]. 北京：中国环境科学出版社，1997.

[2] 曹俊，熊中楷. 闭环供应链的研究进展综述及评价[J]. 物流技术，2010(7):126-129.

[3] 许宪春，李善同. 中国区域投入产出表的编制及分析[M]. 北京：清华大学出版社，2008.

[4] Stevens B., Treyz G., Lahr M. On the comparative accuracy of RPC estimating techniques[J]. Frontiers of Input-Output Analysis, 1989(18):245-257.

[5] 高廷耀,等. 水污染控制工程[M]. 3 版. 北京：高等教育出版社，2007.

[6] 郑飞. 供应链大系统的协调发展模型探讨[J]. 物流科技，2012(9):87-90.