基于有效缺口应力法的正交异性钢桥面板疲劳评价＊

祝志文，钱六五

（湖南大学 土木工程学院，湖南 长沙 410082）

正交异性钢桥面板因具有良好的结构和经济性能，被广泛应用于各种跨径的桥梁中．然而实际桥梁中正交异性桥面板受力复杂，加之超载现象严重，各种构造细节容易出现疲劳开裂．对于其焊接细节疲劳性能的评价，过去通常采用基于S－N 曲线的名义应力法［1］，但正交异性桥面板的焊接细节应力复杂，名义应力有时难以确定，疲劳寿命结果的离散性可能很大．改进的热点应力法可用于焊趾处的疲劳开裂分析［2］，但不能应用于萌生于焊根、内部焊接缺陷等其他部位的疲劳开裂分析．另外，热点应力需要外推得到，如何有效地避免非线性应力也存在疑问．针对上述方法存在的缺陷，Radaj提出了有效缺口应力法［3］，该法通过某一特定的半径来划分焊趾或焊根区域，进而直接计算缺口根部的线弹性应力，从而回避了缺口处的应力集中问题．目前，该法在焊接结构的疲劳评定上得到了一些应用．

本文从有效缺口应力法的原理出发，分析正交异性桥面板之横隔板弧形切口处，与U 肋连接的2种不同横隔板过渡形式中焊趾和焊根处有效缺口应力，并将计算结果与试验结果进行比较，目的在于评价正交异性桥面板的疲劳寿命．另外，本文运用有限元法分析了不同的U 肋厚度对横隔板与U 肋连接焊缝端部疲劳应力的影响．

1 有效缺口应力法原理

1．1 有效缺口应力法起源

在线弹性条件下，应力集中系数k与（1／ρ）0．5（ρ为缺口半径）成正比，当缺口较为尖锐时，缺口尖端的应力会十分大，甚至会出现应力奇点．这显然与实际情况不符，说明缺口处存在着某种支撑效应．Neuber在文献［4］中提出：当缺口尖端区域的应力和应力梯度较大时，材料内部存在的晶粒取向不同等微观各向异性不再可以忽略，而根据忽略材料微观各向异性的弹性理论求得的弹性应力高于此区域的真实应力，这相当于材料的微观结构支撑约束了弹性应力，这个很小区域的平均直径为微观支撑长度ρ＊．该理论则为微观支撑理论．根据微观支撑理论，理论最大缺口应力并非产生疲劳裂纹的决定性因素，在裂纹萌生一定区域内的平均缺口应力才是产生疲劳裂纹的关键所在．平均缺口应力σm可以通过对理论缺口应力σth沿微观支撑长度ρ＊积分求得，如图1所示．

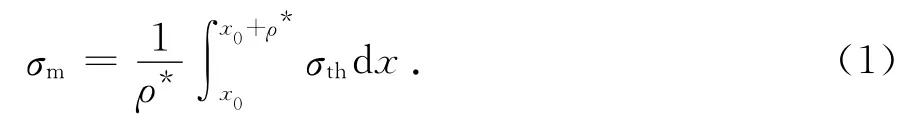
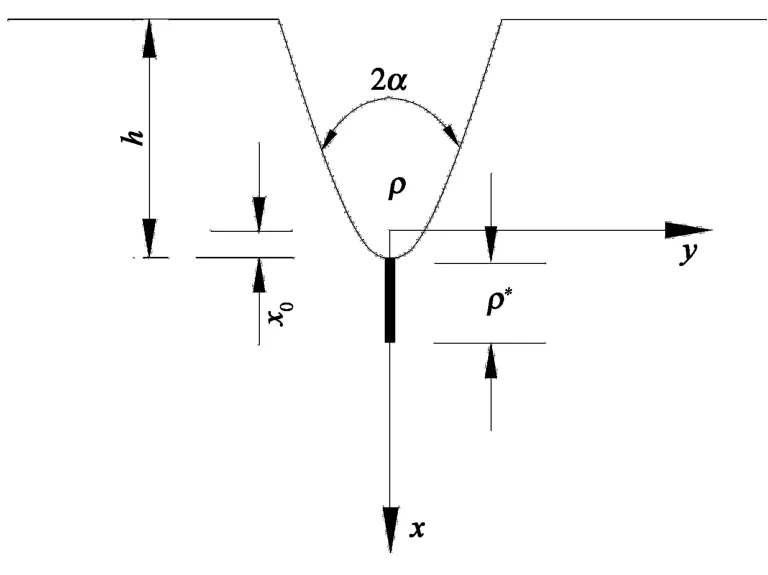
图1 平均缺口应力的计算Fig．1 The calculation of average notch stress

1．2 有效缺口半径推导

公式（1）需对理论缺口应力σth积分，计算较为复杂．为简化求解过程，Neuber提出了新的思路：计算疲劳应力时不需要考虑弹性缺口应力平均值σm，而是直接获得一个包括微观支撑效应在内，反映实际强度减小的最大缺口应力σmax，如图2所示．微观支撑效应可以用虚拟缺口半径ρf 代替真实的缺口半径ρ来反映，见公式（2）：

式中：s为支撑系数．

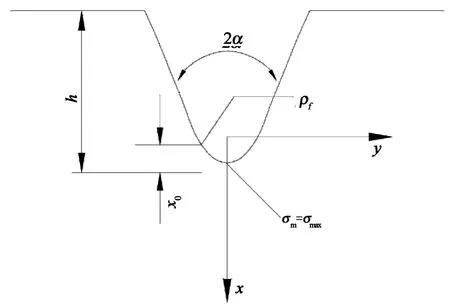
图2 最大缺口应力计算Fig．2 The calculation of the largest notch stress

支撑系数s主要是考虑载荷条件和等效应力对缺口应力的影响，其大小与缺口处的应力状态和适用的强度准则有关，具体见表1．

ρ＊是材料参数，材料发生脆性断裂时，ρ＊是关于材料的断裂韧性KIC和断裂应力σF的函数［5］．

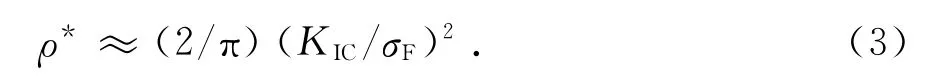
公式（3）计算值偏大，对于高周疲劳，建议采用下式［4］：

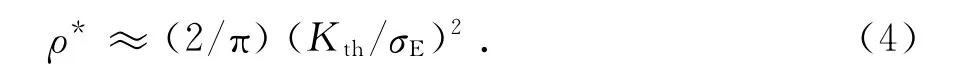
式中：Kth是应力强度因子阈值；σE是疲劳极限．

表1 不同条件下缺口试件的支撑系数Tab．1 Support factor for notched specimen under different conditions

基于大量的疲劳实验，Neuber认为ρ＊是材料屈服极限σY0．2（无明显屈服的钢材，规定以产生0．2%残余变形的应力值为其屈服极限）的函数［4］，不同材料的微观支撑长度如图3所示．

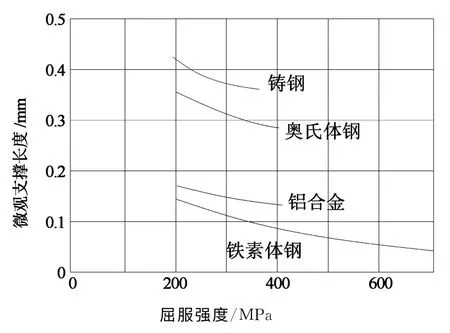
图3 不同材料的微观支撑长度Fig．3 Substitute microstructure length for different materials

对桥梁常用钢材，Radaj建议s取2．5（假定焊缝处于平面应变状态，强度理论为冯米塞斯多轴强度理论），ρ＊取0．4mm．当缺口根部处于最不利情况时（缺口的真实半径ρ＝0），根据公式（2）可计算出ρf ＝1mm，此时：

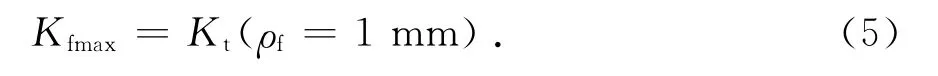
式中：Kfmax为最大疲劳缺口系数；Kt为应力集中系数．

因此，有效缺口应力可以通过虚拟半径ρf ＝1 mm 来划分焊趾和焊根区域，进而求得缺口根部的线弹性应力，如图4所示．

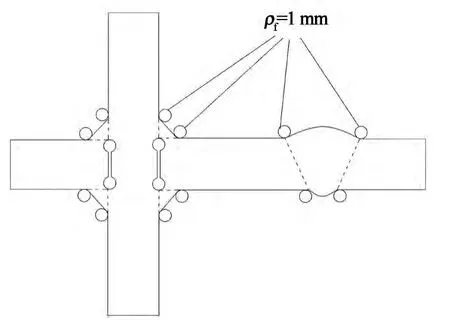
图4 焊趾和焊根处的虚拟圆Fig．4 Fictitious rounding of weld toes and weld roots

当板厚t＜5mm 时，ρf ＝1mm 会使承载截面（尤其在焊根处）显著减小，导致所关心区域的应力偏大．为了避免模型计算误差，Zhang［6］建议此时缺口根部的虚拟半径ρf ＝0．05mm．不过，桥梁焊接构件的板厚很少有小于5mm 的情况．

1．3 有效缺口应力法的计算

虚拟缺口半径ρf 是一个理想化的假定，因此有效缺口应力法通常利用有限单元法或者边界单元法去模拟真实的焊缝应力状态．

有限元计算时，网格质量直接关系到计算结果的精确性．为此，国际焊接协会（IIW）对缺口处网格大小做了详细的规定［7］，见表2．

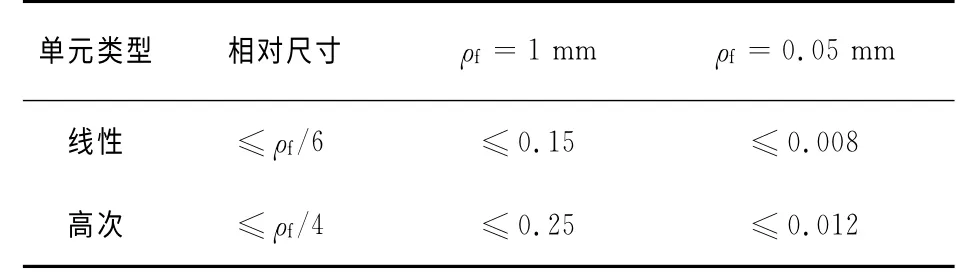
表2 沿着缺口表面的单元尺寸Tab．2 Elements size along the notch surface mm

不难发现，上述方法在有限元建模时不仅顾及了结构整体的几何效应，而且考虑了焊缝细节的几何效应，因此可用一条通用的S－N 曲线评价各种不同类别焊缝的疲劳强度．规范规定［7］：基于正应力评价焊接细节时，当循环次数N＜107次时，S－N 曲线的斜率m为3；在循环次数N＞107次后，S－N 曲线的斜率m为22．同时，当虚拟缺口半径ρf 为1mm时，焊接细节的FAT 值（N＝2×106次循环时材料的疲劳强度）为225 MPa．

然而，上述规范并没有解释FAT 值适用的应力假定以及ρf 为0．05 mm 时 钢 材 的FAT 值．为此，Sonsino在文献［8］给出了不同半径和强度假定下的FAT 值，见表3．表中，主应力假定主要应用于脆性材料，而冯米塞斯力假定主要应用于延性材料以及多轴应力状态．

2 正交异性桥面板的应用

2．1 试验概述

如前所述，实际桥梁中正交异性桥面板受力复杂，加之超载现象严重，各种焊接细节容易出现疲劳开裂．虽然设计及制造时采用了各种措施，但横隔板与U 肋连接处的焊缝仍会出现疲劳裂纹．该处裂纹产生的原因主要有车轮荷载位于横隔板之间时产生的面外弯曲应力和车轮荷载位于横隔上时产生的隔板平面内弯剪复合应力2种．关于隔板面外弯曲应力，AASHTO 规范已做了详细划分，而隔板平面内的弯剪复合应力目前却未有规范明确规定．

文献［9］的疲劳试验主要是评估车轮荷载位于横隔板时，正交异性桥面板之横隔板弧形切口与U肋连接焊缝端部构造细节的疲劳寿命．试件在横隔板弧形切口处选取了2种不同的圆弧过渡形式，目的在于通过实验结果对比获得有利于工程实践的构造形式．2种不同的疲劳试样分别为：圆弧相切过渡（S1）与圆弧垂直过渡（S2），如图5和图6所示．

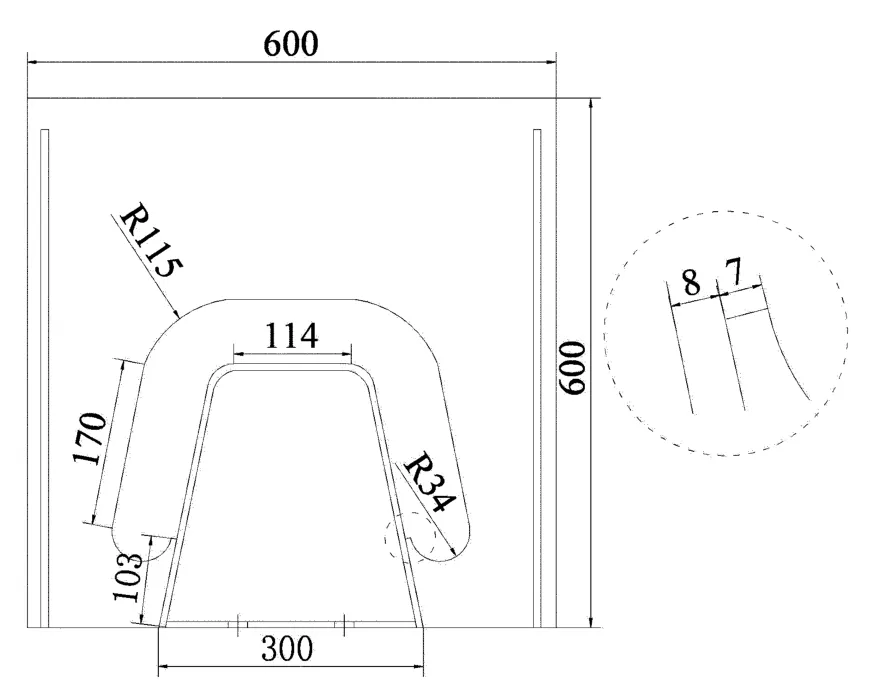
图5 圆弧相切过渡（单位：mm）Fig．5 Circular arc transition（unit：mm）

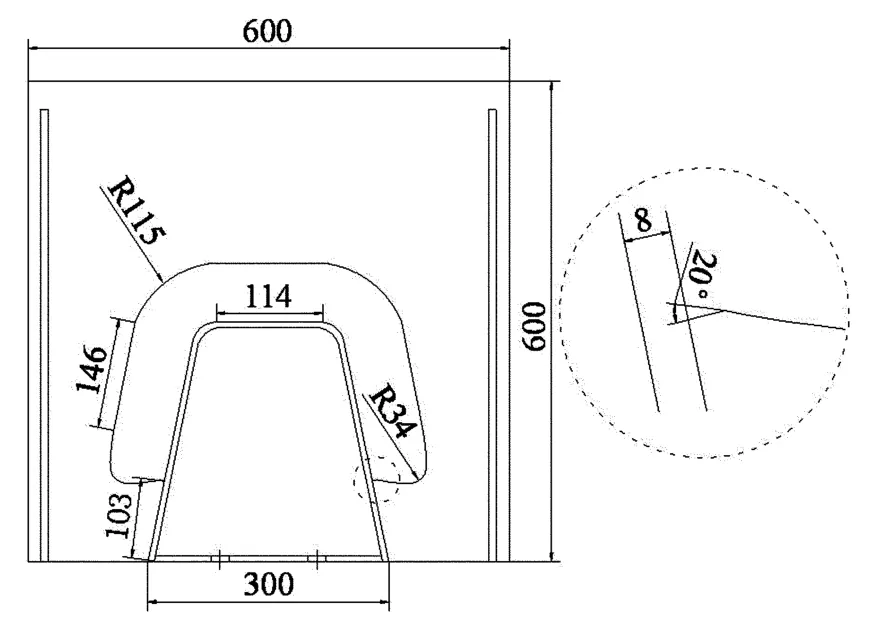
图6 圆弧垂直过渡（单位：mm）Fig．6 Circular vertical transition（unit：mm）

为模拟车轮荷载通过横隔板时隔板平面内的弯剪复合应力，试验时将试件倒置在疲劳机上，面板通过螺栓与固定在地面的钢板连接，如图7所示．试验过程中试件1（S1）采用5种不同的荷载幅，分别为120kN，150kN，180kN，200kN，270kN；试 件2（S2）采用荷载幅180kN，以和试件1（S1）的疲劳实验结果对比．疲劳机采用等幅加载，应力比R＝0，加载频率f为2Hz．

图7 疲劳试验照片Fig．7 Photo of fatigue test

构件失效以疲劳裂纹长度达到20～30 mm 为准则，试验结果见表4．

所有试件的疲劳破坏均发生在横隔板弧形切口与U 肋连接的端焊焊趾处，焊根处无疲劳破坏，如图8所示．

2．2 有限元计算

有限元计算有效缺口应力时，可以选择2D板单元和3D实体单元建模．通常情况下，正交异性桥面板的构造和受力较为复杂，3D实体单元能更好地反映实际的受力状态．因此，建模时建议选用3D实体单元．

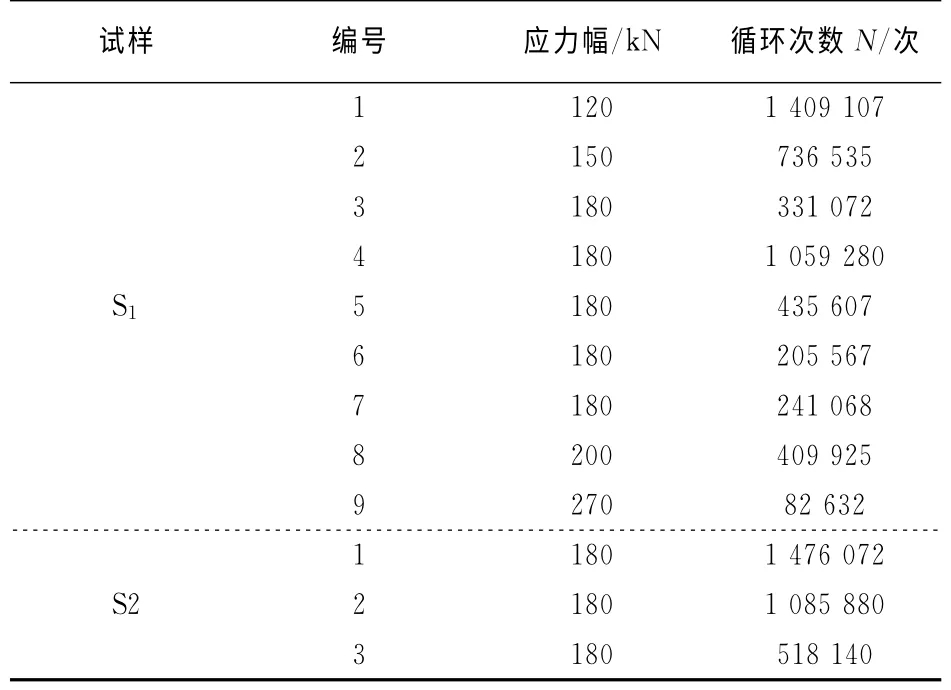
表4 疲劳试验结果Tab．4 Fatigue test results

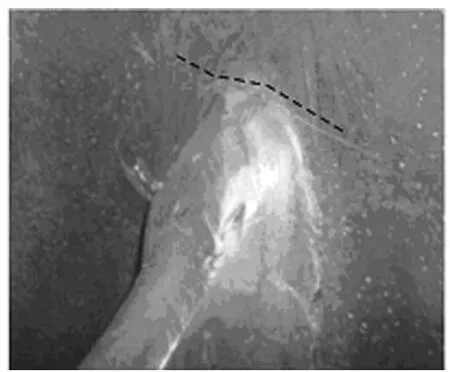
图8 S1焊趾处疲劳裂纹Fig．8 Fatigue crack in weld toe for S1

本文有限元分析时采用与试验一致的荷载幅值加载到疲劳试件上，桥面板处采用固结处理．由于缺口处需要很高的网格分辨率，为减少计算量，根据结构和载荷条件的对称性，选取1／4模型，如图9和图10所示．

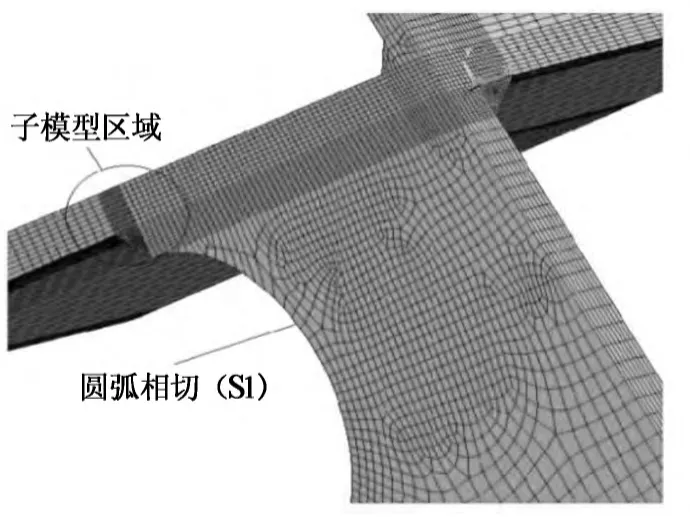
图9 正交异性桥面板整体的网格划分（S1）Fig．9 Global meshing of the investigated orthotropic bridge deck for S1

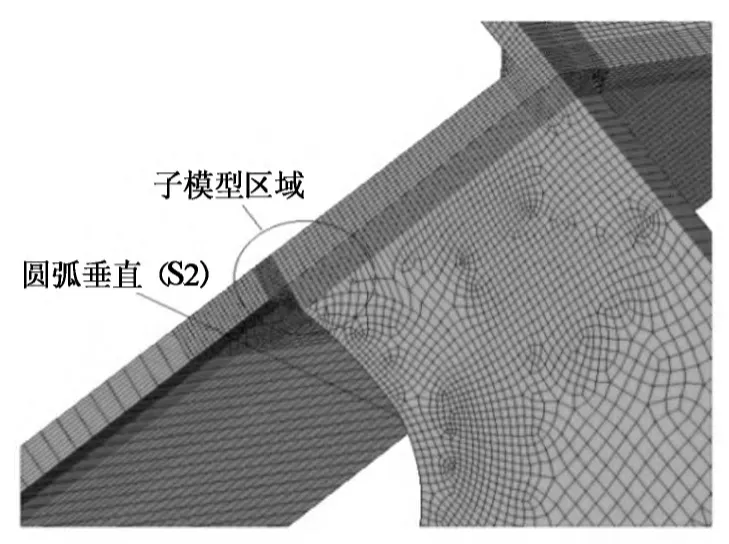
图10 正交异性桥面板整体的网格划分（S2）Fig．10 Global meshing of the investigated orthotropic bridge deck for S2

正交异性桥面板建模时采用了子模型技术对关键细节进行局部细化，如图11和图12所示．子模型技术是基于圣维南原理，即当作用于弹性体表面某一区域的载荷被另一等效载荷替代时，只会对载荷替换区域附近的应力分布有影响，对此外大部分区域的应力影响可忽略不计．为保证计算结果的准确性，建模时应使切割边界远离应力集中区域，一般通过比较子模型切割边界上的应力与粗糙模型相应位置的结果是否一致来验证．

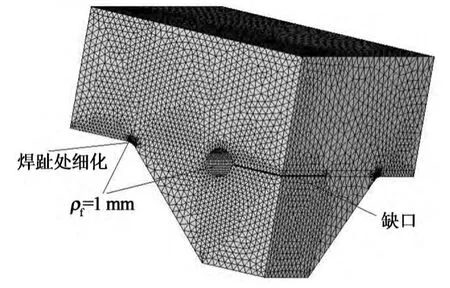
图11 子模型的细节（S1）Fig．11 Details of sub－model for S1

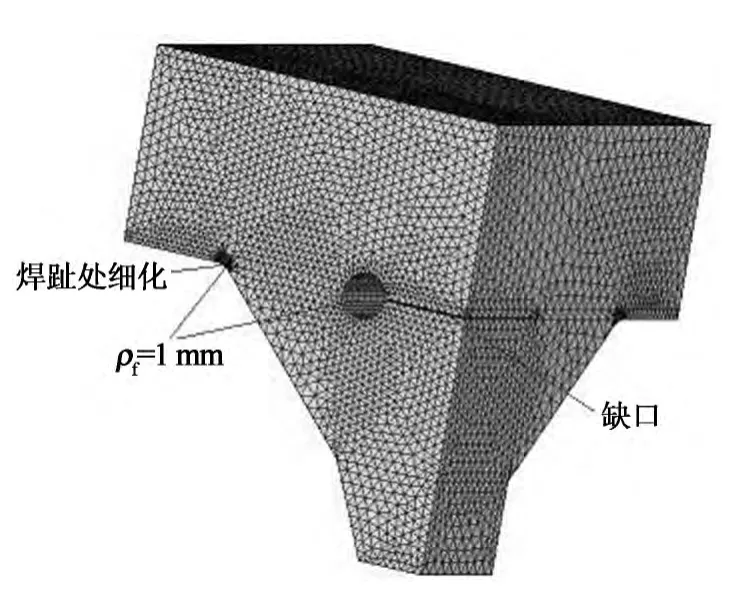
图12 子模型的细节（S2）Fig．12 Details of sub－model for S2

网格质量与有限元计算结果息息相关，因此，本文给出了2套不同的网格尺寸，以做网格无关性验算，如图13和图14所示．其中，方案1沿焊趾缺口区域的单元尺寸为0．1 mm，沿焊根缺口区域的单元尺寸为0．2 mm；方案2 沿焊趾缺口区域的单元尺寸为0．06 mm，沿焊根缺口区域的单元尺寸为0．13mm．上述建模均采用了高次单元，不难发现，所有的网格大小均满足规范的规定值．

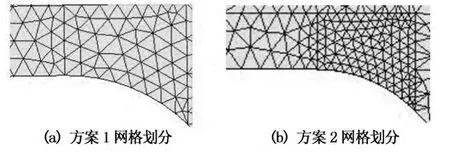
图13 焊趾处的网格划分Fig．13 The meshing of weld toe

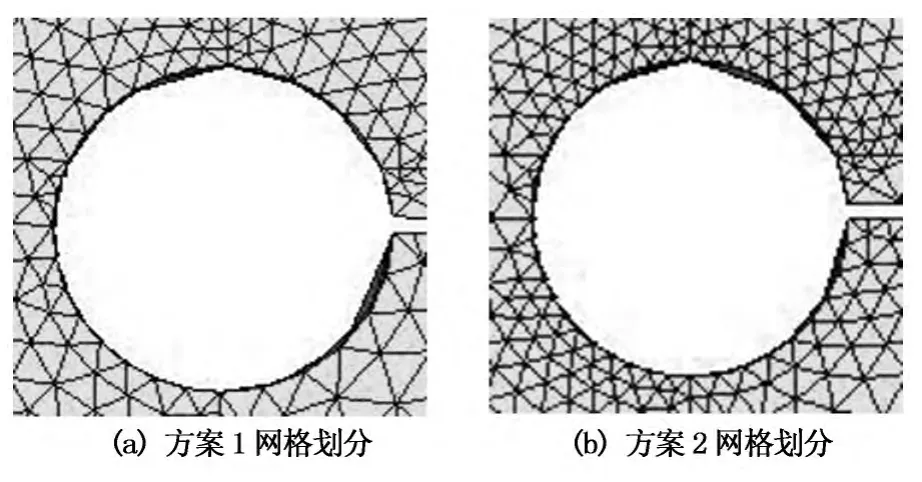
图14 焊根处的网格划分Fig．14 The meshing of weld root

考虑到焊缝处于多轴应力状态，本文应力分析时一律选用冯米塞斯应力．当荷载幅值为120kN时，有限元计算结果如图15和图16所示．

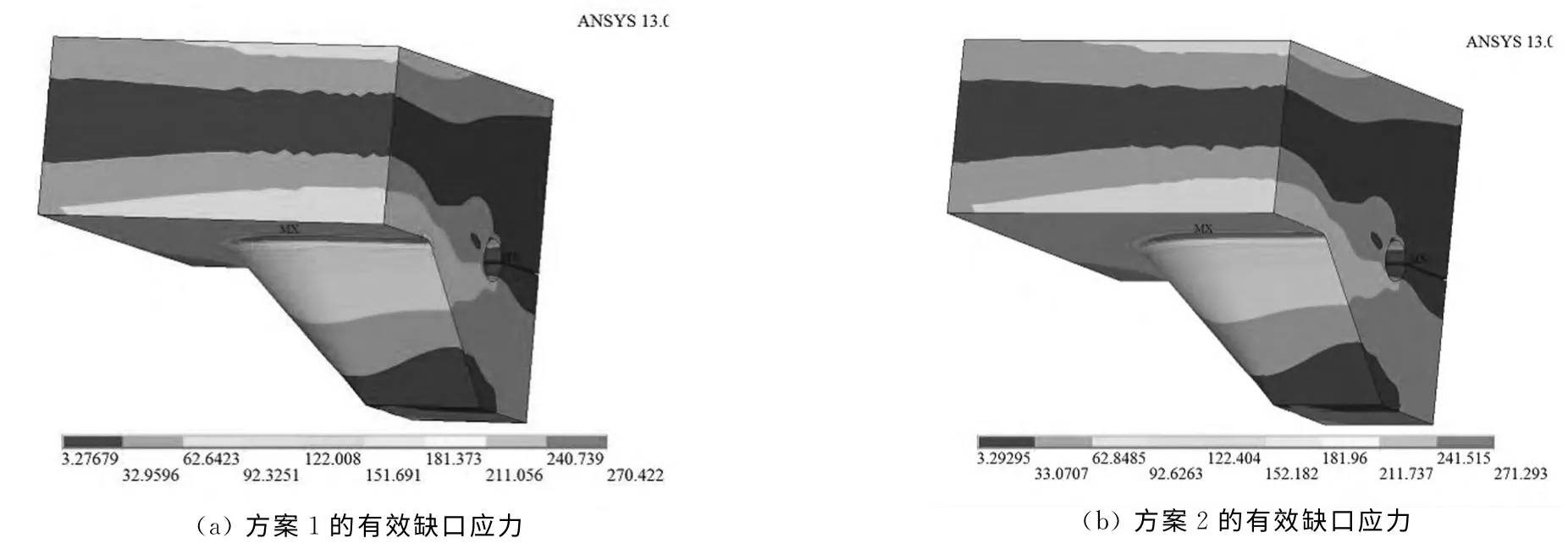
图15 试件S1的有效缺口应力（单位：MPa）Fig．15 Effective notch stresses for S1（unit：MPa）

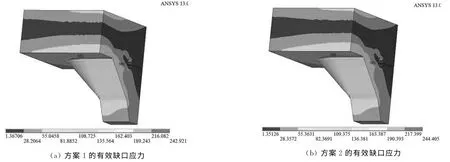
图16 试件S2的有效缺口应力（单位：MPa）Fig．16 Effective notch stresses for S2（unit：MPa）

通过上述计算可得出试件S1和试件S2的有效缺口应力，具体见表5和表6．

从表5和表6可知，在满足规范规定的网格大小条件下，改变网格密度对计算结果影响已很小，几乎可忽略不计，因此上述有限元建模满足网格无关性标准，网格精度符合要求．方案2焊趾和焊根缺口区域的单元尺寸均小于方案1，因此计算的结果较为精确些，应力分析应采用方案2得到的有效缺口应力，具体见表7．

表5 不同网格划分下试件S1焊趾和焊根处的有效缺口应力Tab．5 Effective notch stresses in weld toe and weld root under different meshing for S1 MPa

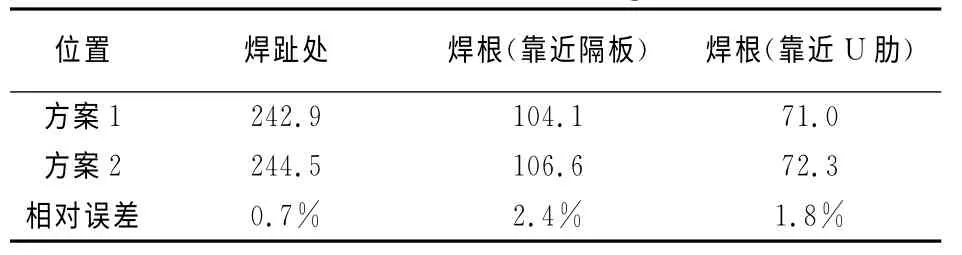
表6 不同网格划分下试件S2焊趾和焊根处的有效缺口应力Tab．6 Effective notch stresses in weld toe and weld root under different meshing for S2 MPa

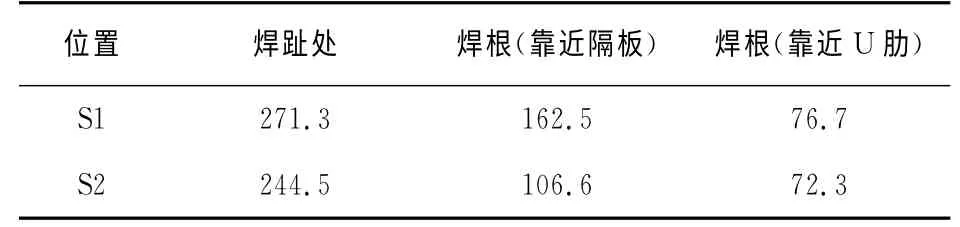
表7 试件S1和试件S2的有效缺口应力Tab．7 The effective notch stress in S1and S2 MPa

从表7可知，试件S1焊趾和焊根处的有效缺口应力均大于试件S2，结果表明试件S1的最大有效缺口应力比试件S2高11%，这与在相同的荷载幅值作用下，试验时试件S2的循环次数要多一些的现象一致．因此相比于试件S1，试件S2的疲劳强度要高一些．对比发现：试件S1和试件S2的焊趾处有效缺口应力均显著大于焊根处的有效缺口应力．其中，试件S1 焊趾处最大有效缺口应力比焊根处高67%，试件S2焊趾处最大有效缺口应力比焊根处高129%，这表明疲劳裂纹更易在焊趾处产生，该结果与加载时所有焊接件均在焊趾处疲劳开裂的现象相同．另外，试件S1靠近隔板侧焊根处的有效缺口应力比靠近U 肋侧高112%，试件S2靠近隔板侧焊根处的有效缺口应力比靠近U 肋侧高47%，因此相比于靠近U 肋侧焊根，技术人员要更注重靠近隔板侧焊根处的焊接质量，以避免疲劳裂纹的产生．

有限元建模时选用了与试验一致的荷载幅值，计算出不同荷载幅值作用下试件S1和试件S2的最大有效缺口应力，具体见表8．

表8 不同加载幅值下试件S1和试件2的最大有效缺口应力Tab．8 The largest effective notch stress for S1 and S2under different load amplitudes MPa

根据上述有效数据，采用有效缺口应力法去评估构造细节的疲劳寿命，其对应的S－N 曲线应满足以下基本关系：

1）基于S－N 曲线评价构件的疲劳强度时，构件疲劳强度的保证率应不低于PS＝97．7%；

2）在疲劳评价中应充分考虑残余应力的影响，通常采用较高的应力比．

残余应力对有效缺口应力法的影响一直是关注的热点［10］．1989 年 和1994 年，Olivier在疲劳试验时就采用了应力比R＝0．4去评价T 型和Y 型焊接件的疲劳寿命；2008 年，Hobbacher进一步地选用应力比R≥0．4分析了不同载荷条件下焊接件在焊趾和焊根处的疲劳破坏；2010 年，Fricke 和Paetzold利用较高的应力比验算了大尺寸模型的疲劳寿命．上述试验结果均表明：在充分考虑残余应力的影响时，IIW 规定的标准S－N 曲线均能保证焊接件的疲劳强度保证率大于99．7%．

近期，Pedersen 通过对比一系列试验数据发现［11］：当板厚较小时，IIW 规范规定的S－N 曲线并不能满足对接焊的试验结果．针对上述状况，Pederson在文章中建议采用较小的FAT 值（建议200 MPa），或者将规范规定的最小疲劳缺口系数Kw从1．6提高至2．0．本文焊接工艺采用的是角焊缝，因此不存在Pederson提出的这种状况．

试验时，二次壳弯曲应力会导致焊接件疲劳应力的增长，因此规范规定有限元计算结果应乘以应力放大系数km，对于角焊缝，规范建议km取1．20［7］，计算结果见表9．

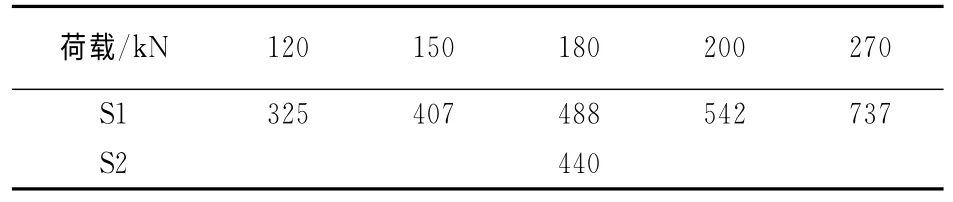
表9 考虑有效应力放大系数时试件的最大有效缺口应力Tab．9 The largest effective notch stress for specimen in consideration of stress magnification factor MPa

参照上述分析，得到基于有效缺口应力法的疲劳试验结果如图17所示．

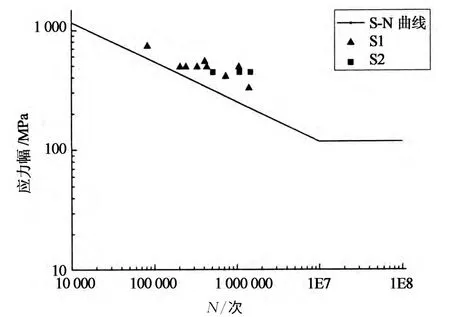
图17 基于有效缺口应力法的疲劳试验结果Fig．17 Fatigue test results based on effective notch stress method

从图17知，试验结果有一定的离散，原因主要来自于两个方面：一是焊接技术、焊接质量、局部缺陷的大小和类型；二是焊接过程残余应力的影响．这就要求我们在以后加工制造时要更加注重正交异性桥面板细节处的焊接质量，避免产生大的质量误差．

试验结果表明：基于有效缺口应力法疲劳评价的正交异性桥面板的试验保证率PS＝100% ，符合要求．图17显示，结果有一定的保守性，这可能与有效缺口应力法中假定缺口的真实半径ρ＝0有关，因为实际正交异性桥面板构造细节处的真实半径一般不为0．

综上所述，虽然结果有一定的离散，但是试验结果满足规范建议的S－N 曲线，这也证明了有效缺口应力法可以很好地应用在正交异性桥面板的疲劳评价中．

2．3 U 肋厚度的影响

实际桥梁中，正交异性桥面板的疲劳裂纹主要出现在桥面板与U 肋连接处，大多数研究也主要关注构造细节对该处的影响，其中包括U 肋厚度与该处疲劳的关系．例如，Sim［12］计算发现U 肋厚度对桥面板与U 肋连接处焊缝的应力几乎没有影响，该处的应力主要受桥面板厚度以及焊缝熔透率影响．而关于U 肋厚度对横隔板弧形切口与U 肋连接的焊缝处细节的疲劳影响却很少有论文涉及．

针对上述问题，本文建模时选取7～11mm5种不同的U 肋厚度去计算横隔板弧形切口与U 肋连接焊缝端部的有效缺口应力．模型选取与圆弧垂直（S2）的横隔板过渡形式，横隔板厚度保持不变，荷载条件同上述实验．选取10mm 的云图，如图18所示，有限元计算结果如图19所示．

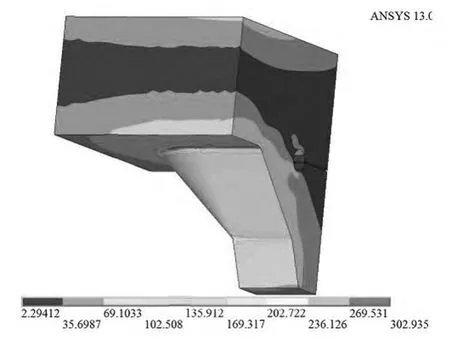
图18 U 肋厚度为10mm 时的应力云图（单位：MPa）Fig．18 Stress nephogram when rib thickness is 10mm（unit：MPa）

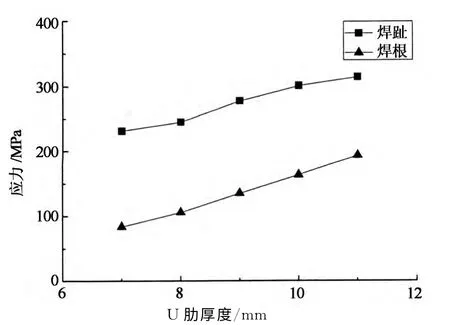
图19 U 肋厚度对焊趾和焊根处最大有效缺口应力的影响Fig．19 The largest effective notch stress in weld toe and weld root under different rib thickness

从图19可知，随着U 肋厚度的增加，焊趾和焊根处的最大有效缺口应力都出现较大程度的增长．结果表明：U 肋厚度的增加非但没有提高结构的疲劳强度，反而更易于横隔板弧形切口与U 肋连接处疲劳裂纹的产生．

3 结 论

1）相比于名义应力法和热点应力法，有效缺口应力法具有更大的优势．通过上述试验分析，验证了有效缺口应力法可以很好地应用于正交异性钢桥面板的疲劳评价中．

2）在充分考虑残余应力的影响时，有效缺口应力法均可应用到疲劳评价中．而上述试验结果具有一定的保守性，这可能与假定缺口的真实半径为0有关，建议开展更大尺寸模型和更多疲劳试验验证方法的精确性．

3）当车辆荷载作用于横隔板时，U 肋与横隔板端焊缝处的焊趾有效缺口应力大于焊根处的有效缺口应力，疲劳裂纹更容易在焊趾处产生．在焊根处，靠近隔板侧的有效缺口应力显著大于靠近U 肋处，因此要更注重靠近U 肋处焊根的细节质量．

4）U 肋厚度对桥面板与U 肋连接处焊缝疲劳几乎没有影响，但当荷载作用于横隔板时，U 肋厚度的增加却导致U 肋与横隔板端焊缝处焊趾和焊根的有效缺口应力显著地增长．因此，增加U 肋厚度非但不能提高结构的疲劳强度，反而更易于U 肋与横隔板端焊缝处疲劳裂纹的产生．

［1］HOBBACHER A F．Fatigue design of welded joints and components［M］．Cambridge：Abington Publishing，1996：21－25．

［2］VAN A M，PACKER J A，WARDENIER J．Criteria for the fatigue assessment of hollow structural section connections［J］．Journal of Constructional Steel Research，1995，35（1）：71－115．

［3］RADAJ D，SONSINO C M，FRICKE W．Fatigue assessment of welded joints by local approaches［M］．Cambridge：Woodhead Publishing，2006：96－101．

［4］NEUBER H．Über die berücksichtigung der spannungskonzentr ation bei festigkeitsberechnungen［J］．Konstruktion，1968，20：245－251．（In German）

［5］WEISS V．Eine bruchmechanik für kerben［J］．Schweiz Arch Angew Wiss Technol，1971，37：1－7．（In German）

［6］ZHANG G，RICHTER B．New approach to the numerical fa－tigue－life prediction of spot－welded structures［J］．Fatigue ＆Fracture of Engineering Materials ＆Structures，2000，23（6）：499－508．

［7］FRICKE W．IIW－2006－09IIW Recommendations for the fatigue assessment of welded structures by notch stress analysis［S］．Cambridge，UK：Woodhead Publishing Limited，2012：34－35．

［8］SONSINO C M．A consideration of allowable equivalent stresses for fatigue design of welded joints according to the notch stress concept with the reference radii rref＝1．00and 0．05 mm［J］．Welding in the World，2009，53（3／4）：64－75．

［9］王斌华，吕彭民，邵雨虹．正交异性钢桥面隔板与U 肋连接热点应力分析［J］．长安大学学报：自然科学版，2013，33（5）：57－63．

WANG Bin－hua，LV Peng－min，SHAO Yu－hong．Analysis of structure of diaphragm－to－rib welded connection in orthotropic steel deck by means of hot spot stress approach［J］．Journal of Changan University：Natural Science Edition，2013，33（5）：57－63．（In Chinese）

［10］FRICKE W，PAETZOLD H．Full－scale fatigue tests of ship structures to validate the S－N approaches for fatigue strength assessment［J］．Marine Structures，2010，23（1）：115－130．

［11］PEDERSEN M M，MOURITSEN O，HANSEN M R，etal．Re－analysis of fatigue data for welded joints using the notch stress approach［J］．International Journal of Fatigue，2010，32（10）：1620－1626．

［12］SIM H B，UANG C M．Stress analyses and parametric study on full－scale fatigue tests of rib－to－deck welded joints in steel orthotropic Decks［J］．Journal of Bridge Engineering，2012，17（5）：765－773．