一种通信卫星天线性能预测技术

雷继兆 王艳丽 李殷乔 袁俊刚 张鸿鹏 孙治国

（1 中国空间技术研究院通信卫星事业部，北京 100094）（2 航天东方红卫星有限公司，北京 100094）

1 引言

通信卫星采用通信天线技术，提供足够的等效全向辐射功率（EIRP）和接收时的天线品质因数（G／T）值，满足地面与卫星间的通信需求。目前，通信卫星正朝着大容量、多功能的方向发展，要求能够为多地区提供通信业务，这使得卫星总体设计中须搭载多副通信天线［1］。通信卫星中，星载天线一般采用反射面式［2-3］。目前，反射面天线的设计和加工已经非常成熟，单天线设计与实际测试结果吻合很好［4］。

然而，随着星载反射面天线越来越多，布局越来越拥挤，在整星构型布局中难免会因星体或其他结构部件的存在，造成散射影响。例如靠近卫星安装板的馈源和反射器会在星体上产生绕射和反射形式的散射，影响天线增益、极化，对EIRP和G／T值造成影响，特别是对存在增益梯度变化较大的滚降区的卫星影响更大，同时多副通信天线间存在耦合，造成卫星电磁兼容性问题，影响了卫星通信性能。

目前，国内对整星条件下天线性能和耦合影响的工作较少，通信卫星天线设计阶段考虑整星影响时一般采用视场分析手段，而以电磁波等效为光线的视场分析对天线的假设不够准确，而且无法考察多副天线间的耦合。为了获取整星条件下通信天线的最终性能，在整星研制阶段安排了无线试验来解决该问题，由于对天线性能恶化没有在设计阶段提前充分识别，在整星阶段依靠测试来验证最终性能，存在技术风险。法国泰雷兹（THALES）公司、美国波音、洛马等公司在通信卫星研制过程中已经针对天线星体相互耦合影响问题，开展了深入的技术研究工作，并已开发了标准的软件工具对该问题在设计阶段加以解决。

本文提出采用GRASP软件中的几何绕射理论（GTD）算法［5-6］，对整星条件下通信卫星天线性能和耦合影响进行分析，此方法可应用于卫星总体设计阶段，优化天线性能和布局，从而改善整星电磁环境，提前规避技术风险。

2 GRASP软件GTD 算法说明

GTD 算法是基于射线的电磁学算法。将电磁波等效为射线，在散射体表面反射，在散射体边缘绕射［7-8］。计算的总电场Ez为反射场Ef和绕射场Er的总和。

反射和绕射射线遵从广义费马原理。广义费马原理认为反射和绕射射线按照最短路程传播。

GTD 算法的核心是射线寻迹。反射和绕射射线遵循反射定律和绕射定律，反射和绕射示意如图1所示。

反射定律：

式中：lx为x方向反射标量；r1为反射点到源点的单位矢量；r2为绕射点到反射点的单位矢量；tx为反射点x方向的切向单位矢量。

图1 反射、绕射射线寻迹示意图Fig．1 Ray tracing of reflection and diffraction

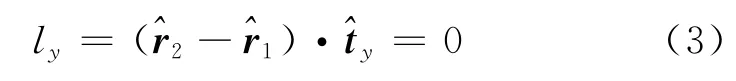
式中：ly为y方向反射标量；ty为反射点y方向的切向单位矢量。

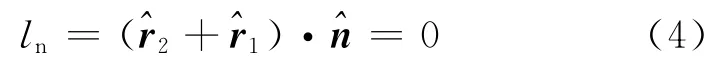
式中：ln为法向反射标量；n为反射点的法向单位矢量。

绕射定律：

式中：ld为绕射标量；t为绕射点的切向单位矢量。

对于多散射体的寻迹问题，通常采用数值寻迹算法，对每条反射和散射路径进行计算，得到总函数：

式中：fR为反射标量平方和平均值。

式中：fD为绕射标量平方和。

式中：F为反射绕射标量总和；N为反射射线的数目，M为绕射射线的数目。

若F＝0，则反射定律和绕射定律均满足，即为正确的射线路径。其次对反射和绕射射线进行遮挡判断，如果射线路径被物体遮挡，则对射线进行排除。

根据射线类型的不同，射线场的求解公式也不尽相同，然而无论反射场还是绕射场存在一个一致性的表达形式：

式中：R0为观察点；Q表示各种射线形式的作用点，如反射时的反射点、绕射时的绕射点等；是一个并矢，表示各种射线形式的并矢作用系数，如反射时的并矢反射系数等；A（s）表示场沿射线的振幅衰减因子；e-jks则是相应的相位衰减因子。场值求解，主要解决的是并矢的求解，它由曲面的几何信息以及射线寻迹的作用点决定。

天线间的耦合度表达式如下：

式中：C为天线间的耦合度，k为波数，r为两副天线间的距离，Et（θt，φt）为发射天线在接收天线方向的方向系数，Er（θr，φr）为接收天线的方向系数。

耦合度可以用dB 表示为CdB＝log20｜C｜，因此，如果CdB＝-80dB，表示当发射天线以1 W 的功率发射时，接收天线接收到的功率为10-8W。

3 实际应用

3．1 星载受扰方向图

仿照某通信卫星构造一个卫星模型，东西板各安装两副偏置赋形单反射面天线。西天线工作频率为6GHz，机械口径尺寸为2．3m，采用水平和垂直双线极化工作。东天线工作频率为13．75GHz，机械口径尺寸为1．8m。对地面上安装两副赋形格里高利双反射面天线，工作频率13．75Hz，机械口径尺寸为0．85 m。卫星平台本体包络尺寸为2．1 m×2．4m×3．7 m，太阳翼尺寸为12．16 m×2．36 m。卫星整体模型如图2所示，采用整星坐标系，坐标原点位于卫星本体中心，＋X轴指向卫星东板，-X轴指向卫星西板，＋Z轴为卫星对地面方向。

图2 通信卫星模型Fig．2 Telecommunication satellite model

本文采用GRASP软件中的GTD 算法，对东西天线进行了单天线和整星情况下的波束覆盖区仿真，图3和图4给出了东天线和西天线受星体影响前后的增益覆盖区，图5给出了西天线受星体影响前后的交叉极化隔离度覆盖区，其中实线为单天线结果，虚线为受星体影响后的结果。从图3～5中可以看出，由于受到星体散射和绕射的影响，某些区域在受星体影响后，天线增益和交叉极化隔离度（XPD）下降到指标线以下，不能满足卫星技术指标要求，该地区的通信质量将受到影响，表1给出了通信天线受到星体影响后覆盖区域内的指标符合性百分比。由此可见，开展整星条件下通信天线性能分析是很有必要的，可以对整星条件下天线性能进行预测，提前发现和规避风险。

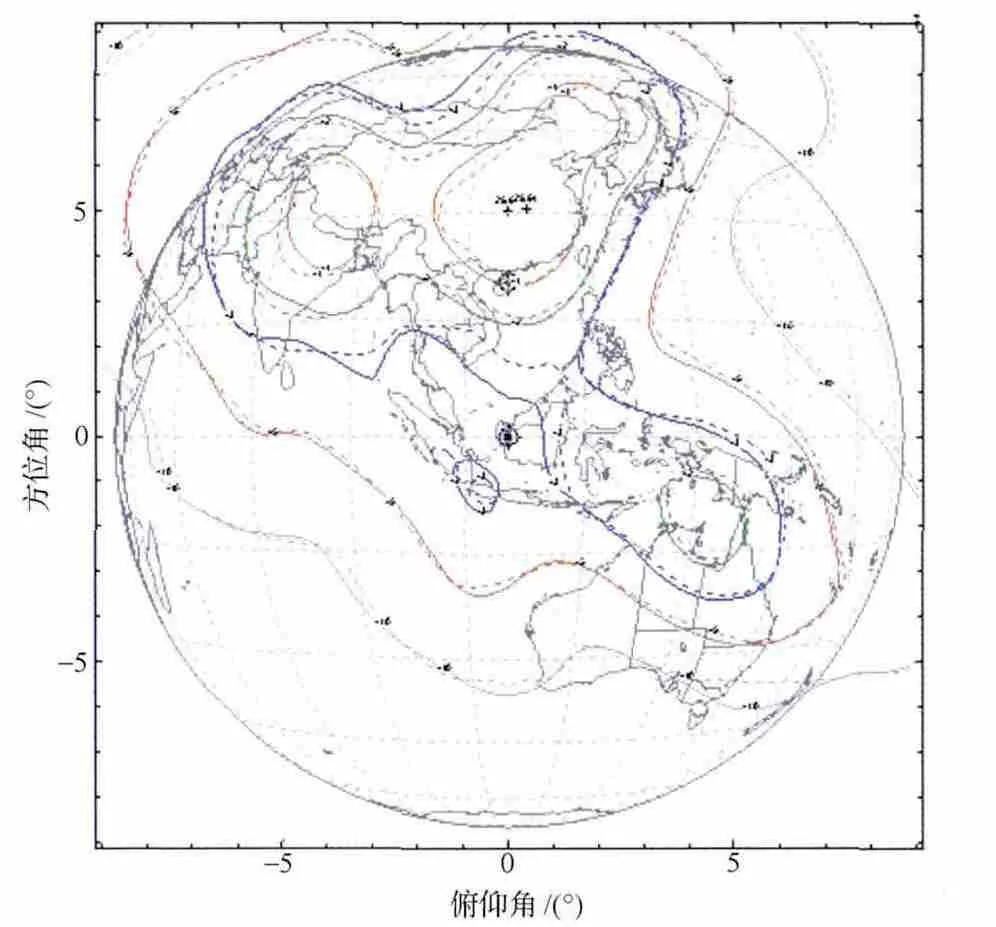
图3 西天线受星体影响前后波束覆盖区Fig．3 Beam contours of west antenna with and without satellite body

图4 东天线受星体影响前后波束覆盖区Fig．4 Beam contours of east antenna with and without satellite body

图5 西天线受星体影响前后XPD 覆盖图Fig．5 XPD contours of west antenna with and without satellite body

表1 有无星体天线性能变化统计Table 1 Differences of antenna performance with and without the satellite body

3．2 星载天线间耦合度

由于通信卫星信道存在非线性，产生的互调杂波会通过天线耦合进入其他信道中产生杂波干扰。因此，通过优化天线布局来降低天线间耦合影响，可以提高卫星电磁兼容性能。针对在对地面上安装的双反射面天线，采用式（10）的耦合度计算原理，本文从两方面进行了耦合度分析。

（1）将反射面天线2沿着Y向从-0．5m 向＋0．5m平移，如图6（a）所示，计算耦合度曲线，如图6（b）所示，可见在这段范围内平移时，天线间耦合度在-52．25dB 到-64．13dB 间变化，在位置-0．03m处，天线间耦合度最小，为-64．13dB。

（2）将反射面天线2沿着主反射器顶点坐标系定义的＋Z轴旋转-180°到180°，如图7（a）所示，计算耦合度曲线，如图7（b）所示，可见在这段范围内旋转时，天线间耦合度在-53．24dB到-65．77dB之间变化，在旋转角为90°处，天线间耦合度最小，为-65．77dB。

可见通过优化天线间的布局，可以将两副天线间的耦合度降低一个量级，显著减少了多副天线间的相互耦合。因此，在进行卫星总体布局设计时，可以按照天线间耦合度最小的位置进行布局，尽量降低天线间的耦合影响，从而改善卫星电磁兼容环境。

图6 移动反射面天线的耦合度Fig．6 Coupling of moving reflector antenna

图7 旋转反射面天线的耦合度Fig．7 Coupling of rotating reflector antenna

5 结束语

预测整星条件下的天线性能已经成为通信卫星总体设计的重要课题。本文针对通信卫星天线逐渐增多，受星体或其他结构部件散射，电磁环境日益恶劣的问题，提出采用GRASP 软件中的GTD 算法，可以对通信卫星天线性能进行提前预测，分析结果表明：

（1）卫星星体和天线布局对通信天线增益和天线间耦合度会产生显著影响，提前开展整星条件下天线性能预测是很有必要的；

（2）对于采用多副天线的通信卫星，在完成整星构型布局设计后，应对通信天线在整星上的布局进行分析，对整星条件下的天线性能和天线间的耦合进行优化，可以提前规避风险。

（References）

［1］陈道明．通信卫星有效载荷技术［M］．北京：中国宇航出版社，2001 Chen Daoming．Payload technique of telecommunication satellite［M］．Beijing：China Astronautics Press，2001（in Chinese）

［2］梁昌洪．简明微波［M］．北京：高等教育出版社，2009 Liang Changhong．Concise microwave［M］．Beijing：Higher Education Press，2009（in Chinese）

［3］魏强．东方红-4卫星平台应用的新突破——中星-11卫星［J］．国际太空，2013（6）：32-36 Wei Qiang．A new breakthough of DFH-4—Chinasat-11［J］．Space International，2013（6）：32-36（in Chinese）

［4］刘志全，杨帆，李全明．航天器赋形反射面数传天线的可靠性评估［J］．航天器工程，2014，23（2）：100-103 Liu Zhiquan，Yang Fan，Li Quanming．Reliability assessment of shaped-beam data transmission antenna of spacecraft［J］．Spacecraft Engineering，2014，23（2）：100-103（in Chinese）

［5］田彪，刘洋，徐世友，等．基于几何绕射理论模型高精度参数估计的多频带合成成像［J］．电子与信息学报，2013，35（7）：1532-1539 Tian Biao，Liu Yang，Xu Shiyou，et al．Multi-band fusion imaging based on high precision parameter estimation of geometrical theory of diffraction model［J］．Journal of Electronics ＆Information Technology，2013，35（7）：1532-1539（in Chinese）

［6］Ji Zhao Lei，Chang Hong Liang．Study on MPI-based parallel modified conformal FDTD for 3-D electrically large coated targets by using effective parameters［J］．IEEE Antennas and Wireless Propagation Letters，2008（7）：175-178

［7］R G Kouyoumjian，E H Pathak．A uniform geometrical theory of diffraction for an edge in aperfectly conducting surface［J］．Proceedings of IEEE，1974，162（11）：1448-1461．

［8］P Persson，L Josefsson．Calculating the mutual coupling between apertures on a convex circular cylinder using a hybrid UTD—MoM method［J］．IEEE Transactions on Antennas and Propagation，2001，49（4）：672-677