俯仰阻尼导数分量的CFD数值模拟

席柯，阎超*，黄宇，王文，袁武

(1.北京航空航天大学 航空科学与工程学院，北京100191;2.中国科学院 计算机网络信息中心，北京100190)

飞行器动态稳定性导数(工程上常称为“动导数”)是飞行器动态气动特性设计、弹道设计及动态稳定性分析中的关键参数.动导数是分析飞行器动态品质和设计操控系统的原始气动数据，动导数的准确评估对飞行器设计和飞行都有重要的意义.

传统上，采用绕定轴俯仰振动(强迫振动或自由振动)方法得到的是俯仰阻尼导数的组合形式Cmq+，即直接阻尼导数(或称旋转导数)Cmq和洗流时差导数(或称加速度导数)的组合.传统位势流理论认为:时差导数在组合导数中所占的比例较小，采用Cmq+代替Cmq误差不大.但是，特别是随着现代科技的进步和战争需求的升级，出现了具有大迎角、超机动飞行能力的飞行器，其外形设计及运动方式都比传统飞行器复杂，流动的非线性及非定常性也更强.上述结论不一定成立，比如大升力体飞行器的时差导数在组合导数中所占比例较大［1］(可达40% ～50%)，并且实际飞行中，飞行器的俯仰角速度和迎角变化率并不总是相等，因此需要分别确定组合导数的各个分量.

目前风洞试验及计算对俯仰阻尼导数分量的研究并不多.一般风洞提供的是直匀流，不能进行直接阻尼导数Cmq的试验.国内，任玉新［2］求解流动控制方程的敏感性方程，直接得到阻尼导数的各个分量，并研究了减缩频率的影响，刘伟等人［3］采用强迫沉浮运动形式，数值模拟了高超声速返回舱及弹道外形(HBS)的加速度导数，研究指出在组合导数小于零的情况下，加速度导数的符号可能大于零，起负阻尼作用，属于动不稳定情况.孙海生［4］在低速风洞中进行了加速度导数的试验，指出在α＜30°范围内，加速度导数大约是组合导数的30% ～50%.国外，美国ARL(Army Research Laboratory)的 Weinacht［5-6］及英国的 Qin等人［7］采用定常方法求解锥转运动及螺旋运动，获得了ANSR(Army-Navy Spinner Rocket)和裙状发射体的直接阻尼导数Cmq及时差导数，但该方法只适用于轴对称外形.

本文结合计算流体力学(CFD)技术开展了飞行器俯仰阻尼导数各个分量的数值模拟研究.采用准定常方法直接获得直接阻尼导数Cmq，求解强迫沉浮运动获得洗流时差导数，求解强迫俯仰振动获得俯仰阻尼组合导数Cmq+.通过HBS及基本带翼导弹(Basic Finner)标模进行了数值方法验证及研究，探讨了质心位置对各阻尼导数的影响以及大攻角下各阻尼导数的变化规律，在此基础上计算了日本的再入飞行器Hyflex的各阻尼导数.

1 计算方法

1.1 流动控制方程

流动控制方程为三维非定常可压缩Navier-Stokes方程.一般曲线坐标系中，无量纲化的方程守恒形式为［8］

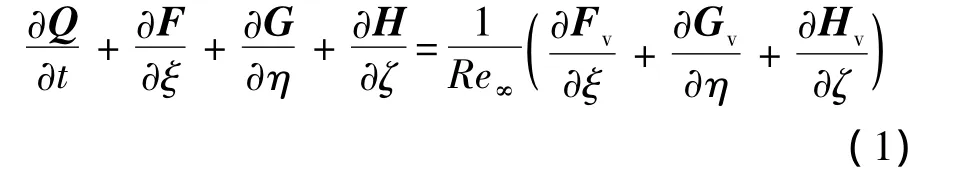
式中，Q为守恒变矢量;F，G和H为对流通量;Fv，Gv，Hv为黏性通量;ξ，η 和 ζ为 3 个贴体坐标系方向;t为时间;Re∞为自由来流雷诺数.

流场求解采用基于结构网格的有限体积法，空间格式采用Roe格式和Minmod限制器，时间离散方法为LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法，非定常时间推进采用双时间步方法.采用SA湍流模型模拟大攻角下可能存在的分离流动，使用Open-MP并行技术提高计算效率.

1.2 直接阻尼导数计算方法

直接阻尼导数的物理意义是由于飞行器的姿态角速度的变化引起各处局部迎角的变化，结果引起质心前后升力之差而产生附加的阻尼力矩，该阻尼力矩对角速度的导数即为直接阻尼导数，它本质上是准定常量.

设体轴坐标系x轴朝前，y轴朝上，z轴满足右手法则.本文采用准定常方法，假设飞行器绕z轴以恒定俯仰角速度q拉起，某瞬时攻角α下有

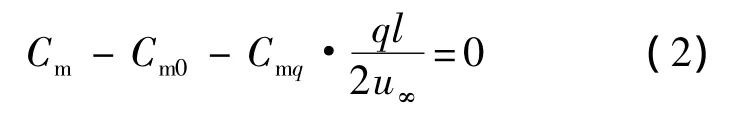
式中，Cm为飞行器以匀角速率q拉起时瞬时攻角α处的俯仰力矩;Cm0为俯仰角速度为零时攻角α处的俯仰力矩;l为特征长度;u∞为来流速度;

Cm0通过定常计算获得;Cm的计算需要考虑俯仰角速度引起的牵连速度的影响以反映局部迎角的变化，本文在空间格式及壁面边界条件中加入牵连速度的贡献，同时网格保持不动，采用准定常方法进行时间推进，经过一段暂态效应，最终力和力矩收敛到定常结果.

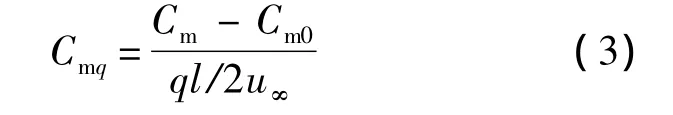
需要说明的是，本文采用的方法不同于文献［5-7］中采用的方法，文献中Weinacht等人在非惯性坐标系下通过在流动控制方程中引入源项来考虑牵连速度的影响，而本文方法是在惯性坐标系下，求解带运动速度物体的瞬态情况，只需将现有求解强迫运动的程序稍作修改即可实现.

1.3 洗流时差导数计算方法

洗流时差导数本质上是非定常量，反映了洗流时差对飞行器的阻尼特性.洗流时差导数的作用体现在飞行器受阵风或直接力作用时飞行器动态稳定性的变化，它是飞行器设计时一个重要的设计参数.

在体轴坐标系，给定沉浮运动形式如下［3］:

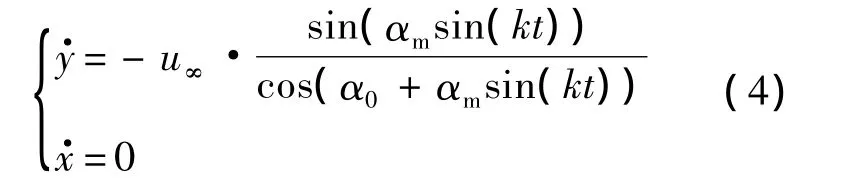
在式(4)描述的运动形式下，可得瞬时攻角的运动形式为

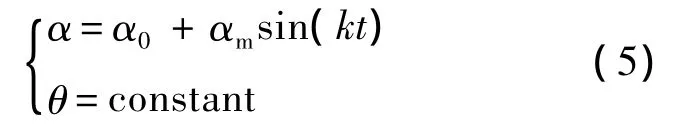
式中，α0为起始攻角;αm为攻角振幅;θ为俯仰角;k为减缩频率.

由式(4)、式(5)确定的沉浮运动中，确定运动的状态变量只有攻角及其各阶导数，根据Etkin非定常气动力模型，Cm可写成

在小振幅运动情况下，将式(6)泰勒展开并略去高阶小量得

俯仰阻尼导数Cmq+的计算采用强迫振动方法，具体数值计算方法参见文献［9-10］.

2 数值模拟结果及分析

本节采用上述数值计算方法，对HBS标模外形及基本带翼导弹外形进行计算验证和研究分析，并在此基础上对Hyflex飞行器进行研究.

2.1 HBS 外形研究

HBS为一个半球柱、带有两段扩张裙部的高超声速弹道外形标模，如图1所示.其动态特性有较为精确的试验结果［11］，常被用来验证计算结果的准确程度.

图1 弹道外形示意图Fig.1 Schematic of hyperballistic shape(HBS)

计算条件为:Ma=6.85，以头部直径为参考长度的 Red=0.72 ×106，质心位置 Xcg/L=0.72，α0=0°，5°，10°，15°，20°.强迫沉浮运动及角振动的减缩频率k定义为:k=ωd/2u∞，d为头部直径.本节计算时取 k=0.01，振幅取 αm=1°.

图2给出了计算得到的俯仰力矩系数曲线.其中图2(a)为HBS外形俯仰角速度取q=0，100，300，500，700，1 000(°)/s 时的俯仰力矩系数变化曲线，可以看出，俯仰力矩系数随俯仰角速度呈完全线性变化，其斜率即为直接阻尼导数，斜率都为负，说明直接阻尼导数为负，起正阻尼作用.图2(b)为强迫沉浮运动时俯仰力矩系数的迟滞环，图2(c)为强迫角振动时俯仰力矩系数的迟滞环，对比两图可以发现，沉浮运动的迟滞环比较瘦，并且0°～15°的迟滞环为顺时针方向旋转，由于迟滞环的旋转方向决定动导数的正负，面积代表动导数的量值大小，这说明HBS的洗流时差导数在俯仰阻尼导数中所占比例较小并且0°～15°的洗流时差导数为正值，其洗流特性是负阻尼的，属于动不稳定情况.而相应的强迫振动的迟滞环比较饱满且各攻角下均为逆时针旋转.

图3为计算所得俯仰阻尼导数与试验值［11］对比，表1为各攻角下直接阻尼导数、洗流时差导数及俯仰阻尼导数的计算结果，其中Cmq+Cmα·为Cmq和直接相加的结果为通过强迫振动直接得到的俯仰阻尼导数，两者误差不超过2%，说明本文发展的计算方法是正确的，并且计算结果是精确的.

图2 弹道外形计算结果Fig.2 Calculation results of hyperballistic shape(HBS)

图3 弹道俯仰阻尼导数计算结果与试验结果对比Fig.3 Calculation and experiment results of pitch-damping derivatives for hyperballistic shape(HBS)

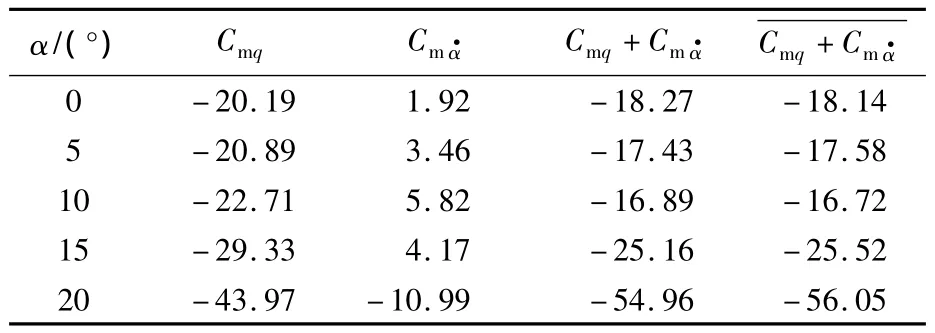
表1 弹道阻尼导数计算结果Table1 Caculation results of pitch-damping derivatives for hyperballistic shape(HBS)

2.2 基本带翼导弹外形研究

基本带翼导弹为一个尖锥形头部、圆柱形弹身并带有4个矩形尾翼的外形，如图4所示.

图4 基本带翼导弹外形Fig.4 Schematic of Basic Finner

计算条件为:Ma=1.96，以底部直径为参考长度的ReD=0.187×106.强迫沉浮运动及角振动的减缩频率k定义为:k=ωD/2u∞，D为底部直径.本节计算时取 k=0.01，振幅取 αm=1°.

图5展示了固定质心位置Xcg/D=6.1时，导弹的直接阻尼导数Cmq、洗流时差导数及俯仰阻尼导数Cmq+随攻角的变化规律(图中曲线采用样条曲线拟合而成，下同).计算攻角为α=0°，2.5°，4°，5°，10°，15°，20°，25°，30°.本文计算的雷诺数与风洞试验［12］中的高雷诺数状态相同.从图5中可以看出，本文计算的俯仰阻尼导数在大攻角时(10°以上)与试验值吻合较好，而小攻角时有一定的偏离.因为试验采用尾支撑方式，Uselton等人［13］注意到小攻角时(6°以下)有较强的支架干扰而导致试验结果重复度较差，直到攻角增大到一定程度才会减弱支架干扰的影响.直接阻尼导数一直为负值，且其绝对值随攻角增大而近似线性增大;时差导数在0°攻角附近为正值，在4°攻角处过零点，然后向负向增大，在10°攻角附近达到负向最大，然后缓慢回落，并一直保持负值.时差导数的非线性变化导致了俯仰阻尼导数的非线性变化，但总体来看，导弹的纵向动稳定性随攻角增大而增强，时差导数符号会有变化，但量值在组合导数中所占比例较小(10%以下).

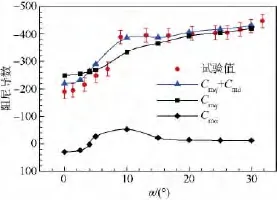
图5 各阻尼导数随攻角变化曲线Fig.5 Variations of pitch-damping derivatives with angles of attack

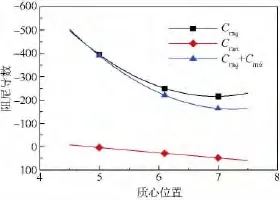
图6 各阻尼导数随质心位置变化曲线Fig.6 Variations of pitch-damping derivatives with center of gravity(CG)location

图6为0°攻角时计算的导弹各阻尼导数随质心位置的变化曲线图.计算的质心位置为Xcg/D=5，6.1，7.从图6中可以看出，时差导数为正值，在质心Xcg/D=5处几乎为零且随质心位置后移而线性增加;直接阻尼导数及组合导数则呈抛物分布，这与文献［14］给出的质心平移关系式(8)～式(10)吻合很好.

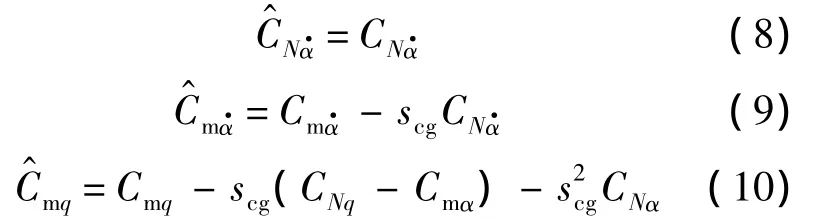
式中scg=(－xcg)/D，坐标定义在体轴系.上式只适用于轴对称物体.

虽然没有在此列出，但计算中CNα，CNq，均为正值，因此时差导数数值随质心后移增加，即朝动不稳定性增大的方向发展.而直接阻尼导数与质心偏移量是复杂的二次函数关系.从数值上来看，存在一个质心位置使俯仰阻尼导数值最大，即动稳定性最差.

2.3 Hyflex外形研究

Hyflex(Hypersonic Flight Experiment)是日本HOPE-X计划中有关大气层再入项目的带翼升力体外形高超声速飞行器，用于验证制导和控制以及热防护材料和结构等技术.它于1996年2月进行飞行试验，本文选取其飞行末端弹道点(马赫2.0，高度30 km)进行研究［15］，该弹道点处于飞行器减速伞开伞前，其动态特性对于减速伞的开启有着至关重要的影响.飞行器外形三视图及网格图见图7.

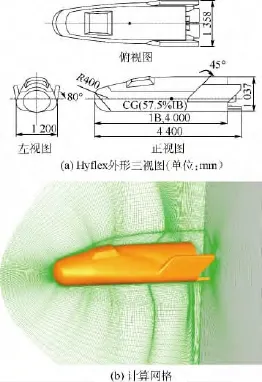
图7 Hyflex外形及网格图Fig.7 Schematic and mesh of Hyflex

计算条件为:Ma=2.0，H=30 km，Sref=4.27 m2，Lref=4 m.计算攻角为:α =0°，5°，10°，15°，20°.减缩频率定义为:k= ωLref/2u∞，本节计算时取 k=0.01，振幅取 αm=1°.

表2给出了各攻角下的直接阻尼导数、洗流时差导数及俯仰阻尼导数计算结果.可以看出，直接计算得到的俯仰阻尼导数与两个分量相加得到的俯仰阻尼导数Cmq+最大相对误差为6%，虽然没有试验数据作为对比，但通过两种不同方法得到的俯仰阻尼导数相差不大，使得本文发展的阻尼导数计算方法的正确性得到了很好的自证.

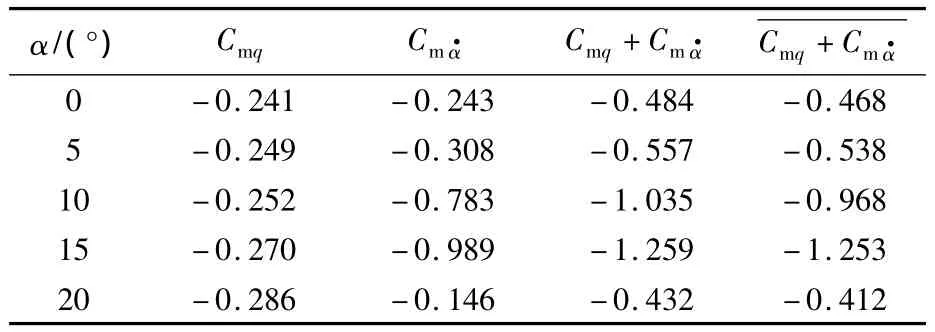
表2 Hyflex阻尼导数计算结果Table2 Calculation results of pitch-damping derivatives for Hyflex

另外，从表2中可以看出，直接阻尼导数为负值，且绝对值随攻角增加而单调增加;洗流时差导数也全为负值，且绝对值先增加后减小，随攻角呈非线性变化，在－15°达到最大，在俯仰阻尼导数中所占比例不再是小量，反而起主导作用(最大比重达78%).与2.1节和2.2节研究的外形相比，Hyflex是带翼升力体外形飞行器，尾部翼面的洗流时差效果更显著.

3 结论

本文研究直接求解俯仰阻尼导数分量的方法，通过对HBS和基本带翼导弹两个标模外形及Hyflex飞行器进行数值模拟研究，结果表明:

1)采用的方法能够准确预测飞行器外形的俯仰阻尼导数的各个分量，即使对于大攻角状态也具有较好的预测精度，具备一定的工程实用价值;

2)对于弹丸类弹道物体，其在超声速及高超声速状态下，洗流时差导数在俯仰阻尼导数中所占比例较小，但其符号可能大于零，起动不稳定作用，并且数值随质心后移而增大;对于带翼飞行器，超声速状态下，洗流时差导数在俯仰阻尼导数中所占比例较大.

直接阻尼导数不论从物理意义上来看还是数值计算都是负值，总起动稳定作用.

References)

［1］ 李周复.风洞特种试验技术［M］.北京:航空工业出版社，2010:210-250.Li Z F.Special wind tunnel testing technology［M］.Beijing:Aviation Industry Press，2010:210-250(in Chinese).

［2］ Ren Y X.Evaluation of the stability derivatives using the sensitivity equations［J］.AIAA Journal，2008，46(4):912-917.

［3］ 刘伟，杨小亮，赵云飞.高超声速飞行器加速度导数数值模拟［J］.空气动力学学报，2010，28(4):426-429.Liu W，Yang X L，Zhao Y F.Numerical simulation of acceleration derivative of hypersonic aircraft［J］.Acta Aerodynamica Sinica，2010，28(4):426-429(in Chinese).

［4］ 孙海生.飞行器大攻角升沉平移加速度导数测量技术［J］.流体力学实验与测量，2001，15(4):15-19.Sun H S.A measurement technique for derivatives of aircraft due to acceleration in heave and sideslip at high angle of attack［J］.Experiments and Measurements in Fluid Mechanics，2001，15(4):15-19(in Chinese).

［5］ Weinacht P.Navier-Stokes predictions of the individual components of the pitch-damping coefficient sum，ARL-TR-3169［R］.Adelphi:Army Research Laboratory，2004.

［6］ Weinacht P.Projectile performance，stability and free flight motion prediction using computational fluid dynamics［J］.Journal of Spacecraft and Rockets，2004，41(2):257-263.

［7］ Qin N，Ludlow D K，Shaw S T，et al.Calculation of pitch damping coefficients for projectiles，AIAA-1997-0405［R］.Reston:AIAA，1997.

［8］ 阎超.计算流体力学方法及应用［M］.北京:北京航空航天大学出版社，2006:18-25.Yan C.The methodology and application of computational fluid dynamics［M］.Beijing:Beihang University Press，2006:18-25(in Chinese).

［9］ McGowan G Z，Kurzen M J，Nance R P，et al.High fidelity approaches for pitch damping prediction at high angles of attack，AIAA-2012-2903［R］.Reston:AIAA，2012.

［10］ Hashimoto A，Hashizume M，Sunada S，et al.Unsteady analysis of aerodynamic derivatives on standard dynamics model，AIAA-2013-0343［R］.Reston:AIAA，2013.

［11］ East R A，Hutt G R.Comparison of predictions and experimental data for hypersonic pitching motion stability［J］.Journal of Spacecraft and Rockets，1988，25(3):225-233.

［12］ Uselton B L，Uselton J C.Test mechanism for measuring pitch damping derivatives of missile configurations at high angles of attack，AEDC-TR-75-43［R］.Tennessee:AEDC，1975.

［13］ Uselton B L，Jenke L M.Experimental missile pitch-and rolldamping characteristics at large angles of attack［J］.Journal of Spacecraft and Rockets，1977，14(4):241-247.

［14］ Murphy C H.Free flight motion of symmetric missiles，NO.1216［R］.Aberdeen:Army Ballistic Research Lab，1963.

［15］ Shirouzu M，Yamamoto M.Overview of the hyflex project，AIAA-1996-4524［R］.Reston:AIAA，1996.