高温结构可靠性分析的时变响应面法

马小兵，任宏道，蔡义坤

(1.北京航空航天大学 可靠性与系统工程学院，北京100191;2.北京航空航天大学 可靠性与环境工程技术国防科技重点实验室，北京100191)

高超声速飞行器在大气环境中的高速飞行具有严酷的气动加热问题［1］，导致飞行器舵面前缘、进气道等部位产生局部高温，威胁飞行器的结构安全.因此进行高超声速飞行器高温结构可靠性分析具有重要意义.目前，高温结构可靠性研究主要分为对结构热响应的确定性分析和结构可靠性分析两部分.其中确定性分析的难点在于气动热和结构热响应的计算.目前主要的研究方式是通过数值模拟来进行气动加热相关的热-温度-结构耦合分析［2-3］.在结构可靠性分析方面，传统的研究思路一般是先建立出结构的极限状态方程，然后利用解析法或数值计算方法求解结构的可靠度等可靠性指标.由于复杂结构的极限状态方程一般没有解析表达式或难以得到显式表达式，一些研究工作将代理模型技术应用在结构可靠性分析中.代理模型技术是以拟合精度为约束，利用近似技术对离散数据进行回归或插值的数学模型.目前常用的代理模型有响应面、人工神经网络、径向基函数、Kriging插值和支持向量机等［4-8］.但是这些方法并不能很好地反映结构可靠度的时变特征［9］，用这些方法计算得到的可靠度实际上是结构在特定时刻的可靠度.当结构可靠度随时间变化范围很小时，采用这些方法具有较好的实用性.然而对于高超声速飞行器的高温结构问题，由于存在快速的升温过程，其承载条件、几何尺寸、材料参数等都会随时间快速、大幅度地变化，这必将导致结构可靠度在工作过程中也有较大变化.传统的结构可靠性模型在解决这类时变问题时需要针对结构典型时刻的状态分别建模并计算可靠度，这样处理只能得到结构在离散时间点上的可靠度且计算效率低下［10-11］.

本文通过对响应面法进行扩展，提出了一种时变响应面法.在综合考虑结构热响应及响应量阈值时变效应的基础上建立了结构时变极限状态函数，给出了结构时变可靠度计算方法，并通过算例验证了该方法的有效性.

1 时变极限状态函数的建立方法

1.1 时变响应面法

响应面法是一种统计学综合试验技术，用于求解复杂系统输出与输入之间关系的近似表达式.传统的响应面法有线性、二阶和高阶等形式.线性形式的响应面法近似能力较差，而高阶形式不仅计算量大，还可能导致在样本点区域的外部出现不稳定等问题［12］，因此一般常用的是带交叉项的二次响应面法，其形式如下:

式中，y表示结构响应量;xi(i=1，2，…，n)表示基本输入变量;αi(i=0，1，…，n)和 αij(i，j=1，2，…，n)均为模型待定系数.

在高速飞行过程中，高超声速飞行器舵面前缘、发动机进气道等局部结构的温度迅速升高，结构的温度场、热应力场等响应量都随时间变化.式(1)只能针对结构特定时刻的响应量建模，不能反映响应量的时变特征.为了针对结构在工作过程中的响应量建模，考虑在传统的响应面函数后面增加与时间有关的函数f(t)，即建立形式如下的响应函数:

只要结构在工作过程中响应量随时间的变化曲线是近似光滑可导的，就能找到一个合适的函数f(t)来拟合响应量随时间的变化趋势.对于高温结构来说，不仅其热响应是一个动态过程，其热响应对于输入参数的灵敏度也是随时间变化的，对式(2)所示的响应函数来说:

其中αij=αji.由上式可见响应函数对基本变量的导数与时间无关，不能反映结构热响应对参数灵敏度随时间的动态变化.为了考虑时间与结构输入参数的耦合效应同时又控制响应面模型的复杂程度，可建立如下形式的响应函数:

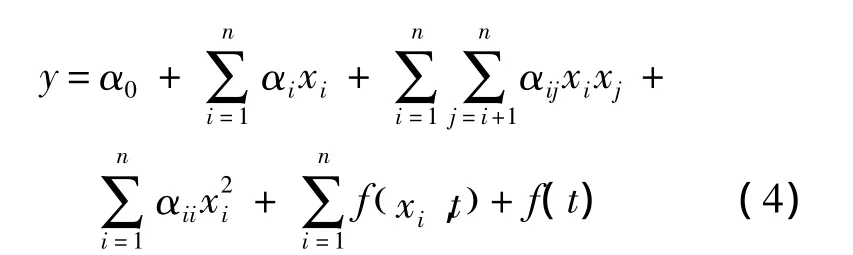
据此:

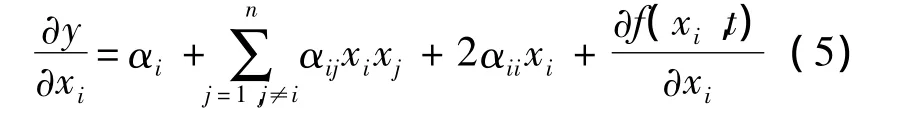
上式反映了结构响应量对参数灵敏度的时变特性.其中f(xi，t)的具体形式需要结合结构热物理方程与样本数据规律来综合确定.

1.2 结构响应量阈值的时变特征

高速飞行器在飞行过程中材料强度、结构屈曲系数等承载指标即响应量阈值也是随时间变化的.为了得到结构的时变极限状态函数，还需要建立结构响应量阈值的时变模型.

通过试验，测试出结构在不同温度下的强度等响应量阈值参数.利用统计方法对样本数据进行拟合，得到结构响应量阈值与温度的近似函数:y′=f(T) (6)式中，y′为响应量阈值;T为温度.

由仿真计算结果或试验测试数据可得到结构在飞行过程中的温度变化数据，对样本数据进行拟合，得到结构温度与时间的函数:

由式(6)、式(7)可以得到结构响应量阈值与时间的近似函数，即

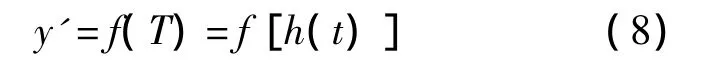
1.3 结构时变可靠度的计算

结构的时变极限状态函数等于结构时变响应量阈值函数与时变响应量函数之差，由式(4)和式(8)得到:

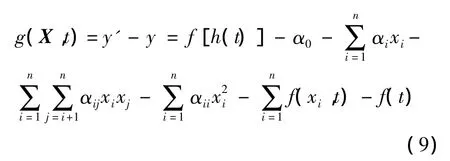
这里，极限状态函数g(X，t)是一个随机过程.为了得到结构时变可靠度等可靠性指标，首先计算其均值μg和标准差σg，其中:

由于结构响应量y与响应量阈值y′相互独立，则

材料的响应量阈值(如拉伸强度等)的变异系数用cv表示，则

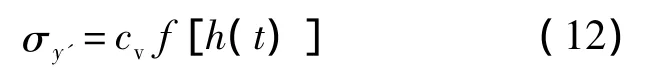
当f(xi，t)不是线性函数时，σy的求解比较困难，可以采用Monte Carlo抽样的方法求得近似解.一般情况下令f(xi，t)=α′ixit即可以得到较好的拟合精度.时变响应量y的方差可表示为

结构可靠度计算公式为

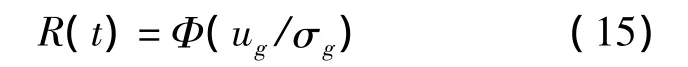
由于均值和标准差均是时间的函数，因此求解得到的可靠度也是时间的连续函数.利用时变响应面法可以计算得到飞行过程中热结构在任意时刻的可靠度.

2 案例分析

飞行器迎流结构通常是飞行过程中气动加热最严酷的部位.下面以某高超声速飞行器的迎流结构为例，对上述高温结构可靠性分析的时变响应面法进行说明.案例分析只考虑热载荷，针对热强度破坏问题进行结构时变可靠性分析，此时结构响应量为热应力，响应量阈值为材料的热强度.

2.1 有限元建模及仿真计算

根据结构设计参数及载荷条件建立有限元模型，采用完全耦合算法仿真计算得到结构的热温度场和热应力场.结果表明前缘部位温度最高、热应力最大，图1为结构前缘点的应力时间历程.

图1 结构前缘点应力时间历程Fig.1 Stress-time relation of the leading edge structure

2.2 结构可靠性分析

2.2.1 试验设计

结构的基本输入变量包括材料参数、结构几何形状、载荷等.这些变量都存在一定程度的分散性.为了简化分析过程，减少计算量，通过多次仿真计算，筛选出对该结构热应力影响最大的3个基本变量:热流密度系数k、材料拉伸模量E以及线膨胀系数α.假设这3个基本变量均服从正态分布，且变异系数分别为 0.1，0.1 和0.01.

常用的响应面试验设计方法有中心复合设计(CCDS)和 Box-Behnken 设计(BBD)［13-14］.本案例属于三水平设计问题，采用BBD设计方法.试验设计得到13组样本输入数据，分别进行有限元仿真计算.由于结构前缘中心点处温度最高、热应力最大，因此选取该单元为研究对象.图2是0～60 s内各组仿真计算所得到的热应力时间历程.

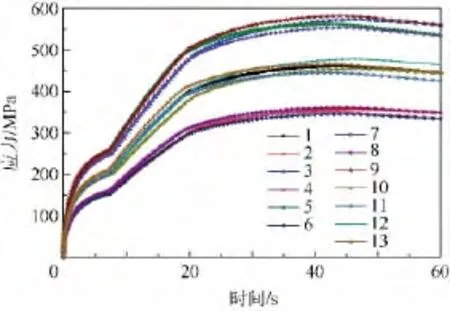
图2 各组样本仿真计算的应力时间历程Fig.2 Stress-time relation of each simulation test

2.2.2 建立热应力的时变响应模型

利用13组仿真计算所得到的样本数据，可以建立时变响应面模型.由于热应力数据在0～20 s和20～60 s这两段时间内的变化趋势差异较大，为了简化响应面形式并提高计算精度，本文将热应力时间历程分为0～20 s和20～60 s两个阶段，分别建立热应力的时变响应面.通过分析仿真计算所得的数据特征可知该问题中结构响应量(热应力)对输入参数的灵敏度的变化趋势较为简单，因此可令式(4)中的 f(xi，t)= αixit，f(t)=b0t+b1t2，从而确定如下形式的响应方程:

采用逐步回归法对有限元仿真计算得到的数据进行回归拟合，得到结构在0～20 s和20～60 s的热应力函数如式(17)和式(18)所示:

2.2.3 材料强度的时变特征分析

采用有限元仿真计算得到迎流结构前缘点的温度时间历程如图3所示.

对超高温陶瓷材料的强度-温度数据［15］进行多项式回归可得到强度与温度的近似函数关系为

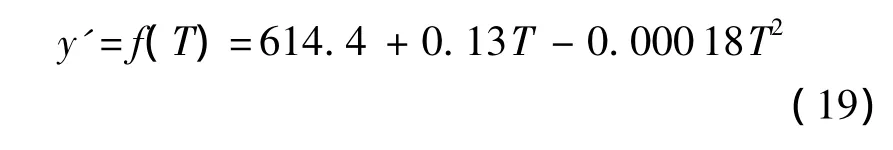
图3 结构前缘点温度时间历程Fig.3 Temperature-time relation of the leading edge structure

将图3中的温度-时间数据代入式(19)中得到材料的强度-时间数据近似函数如图4所示.

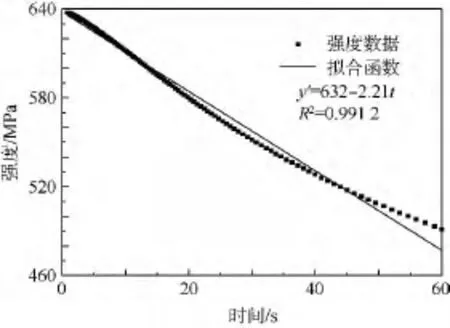
图4 材料强度时变数据Fig.4 Time-varying strength data of the material

2.2.4 可靠度计算结果

由式(9)、式(17)、式(18)和图4中的强度-时间近似函数可得结构极限状态函数为

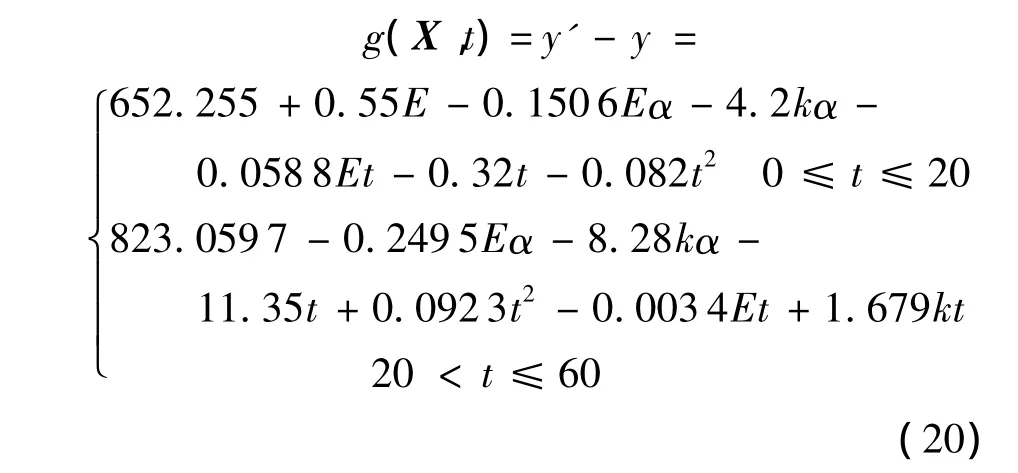
利用式(10)～式(14)计算得到极限状态函数的均值μg和标准差σg，代入式(15)得到结构时变可靠度的表达式:热结构可靠度R随时间的变化规律见图5.可见，结构在初始阶段的可靠度很高.随着气动加热的作用，结构温度上升，材料强度降低，同时结构的温度梯度增大导致热应力增大，因此结构可靠度开始显著下降.在大约55 s后，由于传热作用，结构内的温度分布趋于均匀，温度场梯度开始减小，热应力也随之减小，因此结构可靠度有小幅增大.

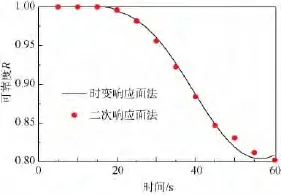
图5 热结构可靠度R与时间的关系Fig.5 Time-varying structural reliability of the high-temperature structure

2.3 结果对比

为验证该方法的准确性，将本文计算结果与传统可靠性分析方法的计算结果进行对比.由于传统的结构可靠性分析模型只能计算结构在特定时刻的可靠度，因此本文选取 5，10，15，20，25，30，35，40，45，50，55，60 s 这 12 个时刻分别采用二次响应面法计算出可靠度，计算结果对比如图5散点所示.二者的平均相对误差为0.05%.

3 结论

1)对结构的热响应建立时变响应面模型并通过逐步回归确定得到待定参数的方法具有较高的精度.本文案例中，采用时变响应面模型对热应力进行拟合的相对误差小于0.1%.

2)考虑材料强度退化效应的高温结构时变响应面法可高效地计算出高温结构可靠度与时间的关系，其在特定任务时间下的计算结果与传统计算方法所得结果一致.由于本文方法不需要针对特定时刻重复建立响应面模型，因此在保证计算精度的同时可大幅提高计算效率.

References)

［1］ Moses P L，Rausch V L，Nguyen L T，et al.NASA hypersonic flight demonstrators-overview，status，and future plans［J］.Acta Astronautica，2004，55(3-9):619-630.

［2］ Joshi O，Pénélope L.Stability analysis of a partitioned fluidstructure thermal coupling algorithm［J］.Journal of Thermophysics and Heat Transfer，2014，28(1):59-67.

［3］ 唐健，吴志刚，杨超.考虑结构刚度不确定性的概率颤振分析［J］.北京航空航天大学学报，2014，40(4):569-574.Tang J，Wu Z G，Yang C.Probabilistic flutter analysis with uncertainties in structural stiffness［J］.Journal of Beijing University of Aeronautics and Astronautics，2014，40(4):569-574(in Chinese).

［4］ Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7(1):57-66.

［5］ 汪保，孙泰.改进的Kriging模型的可靠度计算［J］.计算机仿真，2011，28(2):113-116.Wang B，Sun T.Structural reliability computation based on Kriging model［J］.Computer Simulation，2011，28(2):113-116(in Chinese).

［6］ 吕震宙，杨子政，赵洁.基于加权线性响应面法的神经网络可靠性分析方法［J］.航空学报，2006，27(6):1063-1067.Lü Z Z，Yang Z Z，Zhao J.An artificial neural network method for reliability analysis based on weighted linear response surface［J］.Acta Aeronautica et Astronautica Sinica，2006，27(6):1063-1067(in Chinese).

［7］ 赵卫，刘济科.基于支持向量机回归的迭代序列响应面可靠度计算方法［J］.机械强度，2008，30(6):916-920.Zhao W，Liu J K.Iterative sequence response surface method for reliability computation based on support vector regression［J］.Journal of Mechanical Strength，2008，30(6):916-920(in Chinese).

［8］ 姜潮，黄新萍，韩旭，等.含区间不确定性的结构时变可靠度分析方法［J］.机械工程学报，2013，49(10):186-193.Jiang C，Huang X P，Han X，et al.Time-dependent structural reliability analysis method with interval uncertainty［J］.Journal of Mechanical Engineering，2013，49(10):186-193(in Chinese).

［9］ Chakraborty B，Bhar A.Time-varying reliability analysis using a response surface method for a laminated plate under a dynamic load［J］.Journal of Engineering for the Maritime Environment，2014，226(3):260-272.

［10］ Liu J，Li Y.An improved adaptive response surface method for structural reliability analysis［J］.Journal of Central South University，2012，19:1148-1154.

［11］ Rackwitz R.Reliability analysis:a review and some perspectives［J］.Structural Safety，2001，23(4):365-395.

［12］ Gavin H P，Yau S C.High-order limit state functions in the response surface method for structural reliability analysis［J］.Structural Safety，2008，30(2):162-179.

［13］ Ferreira S L C，Bruns R E，Ferreira H S，et al.Box-Behnken design:an alternative for the optimization of analytical methods［J］.Analytica Chimica Acta，2007，597(2):179-186.

［14］ 付剑平，陆民燕，阮镰，等.试验设计在软件可靠性测试中的应用［J］.北京航空航天大学学报，2008，34(12):1379-1383.Fu J P，Lu M Y，Ruan L，et al.Experimental design for software reliability testing［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(12):1379-1383(in Chinese).

［15］ Song G M，Zhou Y，Kang S J L.Experimental description of thermomechanical properties of carbon fiber-reinforced TiC matrix composites［J］.Materials ＆ Design，2003，24(8):639-646.